Дифференциалдық есептеулердің негізгі теоремалары және оларды әр түрлі есетерде қолдану

КІРІСПЕ 3
1. Дифференциалдық есептеулердің негізгі теоремалары және оларды әр түрлі есетерде қолдану 4
2. Лагранж теоремасы. 5
3. Коши теормасы. 6
ҚОРЫТЫНДЫ 9
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 10

Жұмыстың бірінші тарауында регуляр шекаралық шарттардың әр түріне жеке тоқталып, төртінші ретті дифференциалдық оператор үшін регуляр, оның ішінде күшейтілген және күшейтілген емес шекаралық шарттарды бөліп алып. Сол әр шарттқа сәйкес дифференциалдық оператордың меншікті функцияларының асимптотикасын алып, олардың базис болу болмауын тексереміз.
Шекаралық шарттар күшейтілген регуляр болған жағдайда оператордың меншікті және қосалқы функциялары 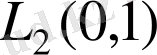кеңістігінде Рисс базисін құратыны белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес операторының нормаланған меншікті және қосалқы функциялар жүйесінің бесселдік екендігіне әкелінді.
Кессельман Г.М. жұмыстарында шекаралық шарттары регуляр бірақ күшейтілген емес регуляр болатын дифференциалдық оператордың меншікті және қосалқы функциялары базис құрмайтындай мысалдар көрсеткен. Себебі бұл жағдайларда оператор Данфорд Н. мағынасында спектральды болмайды, демек бұл жағдайда оператордың меншікті және қосалқы функциялары Рисс базисін құрмайтыны белгілі. Бұл жайтты, оператордың меншікті мәндері асимптотикалық жақын орналасқандығымен түсіндіруге болады, демек келесідей асимптотикаға ие

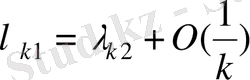
болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы функциялар жүйесі базис құрмайды.
Екінші ретті дифференциалдық операторларға қарағанда төртінші ретті шекаралық шарттары күшейтілген емес регуляр болатын дифференциалдық операторлардың спектральдық теориясы азырақ дамыған. Бұған байланысты тек жекеленген жұмыстар ғана бар.[3,4] Бұл дипломдық жұмыста алдағы уақытта дәл осы шекаралық шарттар күшейтілген емес регуляр болатын төртінші ретті дифференциалдық операторлардың спектральдық қасиеттері зерттеледі.
Ал екінші тарауда екінші ретті дифференциалдық оператордың ойылған кесіндідегі Гельфанд – Левитан формуласы тектес бірінші регуляризацияланған ізі есептелген.

1. Қабдықайыр Қ. Қ13 Жоғарғы математика: Оқулық. - Өңд., толықт., 4-бас. – Алматы, 2005. – 524 б.
2. Есмұқанов М. Математикалық анализ курсы: жоғары оқу орындары студенттеріне арналған оқу құралы. – Алматы: Білім, 1995-248 бет
3. Жолымбаев О.М. «Жоғары математика». Алматы «Эверо» ЖШС, 2004, 98-107 бет.
4. Индивидуальные задания по высшей математике. / Под ред. А.П. Рябушко. – Минск: Высшая школа, 2000. Ч1,2,3.
5. Выгодский М.Я. Справочник по высшей математике. – М., 2000.
6. Қаражанұлы Т. “Математика”. Алматы, 2000, 99-129бет.
7. Фихтенгольц Г.М. “Математикалық анализ негіздері” ,І т Москва 2003.
8. Очан Ю.С., Шнейдер В.Е. «Математический анализ», Москва 2000.

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 9 бет
Таңдаулыға:

ЖОСПАР
КІРІСПЕ 3
1. Дифференциалдық есептеулердің негізгі теоремалары және оларды әр түрлі есетерде қолдану 4
2. Лагранж теоремасы. 5
3. Коши теормасы. 6
ҚОРЫТЫНДЫ 9
ПАЙДАЛАНЫЛҒАН ӘДЕБИЕТТЕР ТІЗІМІ 10

КІРІСПЕ

Жұмыстың бірінші тарауында регуляр шекаралық шарттардың әр түріне жеке тоқталып, төртінші ретті дифференциалдық оператор үшін регуляр, оның ішінде күшейтілген және күшейтілген емес шекаралық шарттарды бөліп алып. Сол әр шарттқа сәйкес дифференциалдық оператордың меншікті функцияларының асимптотикасын алып, олардың базис болу болмауын тексереміз.
Шекаралық шарттар күшейтілген регуляр болған жағдайда оператордың меншікті және қосалқы функциялары кеңістігінде Рисс базисін құратыны белгілі. Бұл айтылғанды ең алғаш В.П. Михайлов көрсетті. Дәл осы нәтиже Кессельман Г.М. жұмыстарында, және Данфорд Н. мен Шварц Т. монографиясында бар. Бұл жұмыстардың барлығында да, дәлелдеу оператор мен оның түйіндес операторының нормаланған меншікті және қосалқы функциялар жүйесінің бесселдік екендігіне әкелінді.
Кессельман Г.М. жұмыстарында шекаралық шарттары регуляр бірақ күшейтілген емес регуляр болатын дифференциалдық оператордың меншікті және қосалқы функциялары базис құрмайтындай мысалдар көрсеткен. Себебі бұл жағдайларда оператор Данфорд Н. мағынасында спектральды болмайды, демек бұл жағдайда оператордың меншікті және қосалқы функциялары Рисс базисін құрмайтыны белгілі. Бұл жайтты, оператордың меншікті мәндері асимптотикалық жақын орналасқандығымен түсіндіруге болады, демек келесідей асимптотикаға ие

болғанда. Соның ішінде жақын орналасқан меншікті мәндерге сәйкес меншікті функциялар бір біріне тең емес, бірақта арасындағы бұрыш нөлге ұмтылады. Дәл осындай жағдайларда оператордың меншікті және қосалқы функциялар жүйесі базис құрмайды.
Екінші ретті дифференциалдық операторларға қарағанда төртінші ретті шекаралық шарттары күшейтілген емес регуляр болатын дифференциалдық операторлардың спектральдық теориясы азырақ дамыған. Бұған байланысты тек жекеленген жұмыстар ғана бар.[3,4] Бұл дипломдық жұмыста алдағы уақытта дәл осы шекаралық шарттар күшейтілген емес регуляр болатын төртінші ретті дифференциалдық операторлардың спектральдық қасиеттері зерттеледі.
Ал екінші тарауда екінші ретті дифференциалдық оператордың ойылған кесіндідегі Гельфанд - Левитан формуласы тектес бірінші регуляризацияланған ізі есептелген.

1. Дифференциалдық есептеулердің негізгі теоремалары және оларды әр түрлі есетерде қолдану
Ферма теоремасы
Егер (а, в) интервалында анықталған у = f (x) функциясы қайсыбір с ∈ (а, в) нүктесінде өзінің осы аралықтағы ең үлкен (ең кіші ) мәнін қабылдайтын болса және f ` (c) туындысы бар болса, онда f ` (c) = 0
Дәлелдеуі: f функциясы c нүктесінде ( a,b) интервалындағы ең үлкен мәнін қабылдасын, яғни fcmax(a,b)f(x). Сонда барлық х ∈ (а, в) үшін fх=fc немесе fх-fc=0. Бұдан xc мәндері үшін
fх-fc x-c =0 (26)
Ал x0 мәндері үшін
fх-fc x+c =0 (26`)
Теореманың шарты бойынша
f `c=limх--0 fх-fc x-c
шегі бар болғандықтан, ол х--0-с жағдайда және х--0+с жағдайда тек бір ғана мәнді қабылдайды. Енді х--0-с жағдайда (26) теңсіздікте шекке көшіп f `c=0 теңсіздігін аламыз. Осылайша х--0+с жағдайда да (26`) теңсіздікте шекке көшіп, f `c=0 теңсіздігін аламыз. Бұл соңғы екі теңсіздіктен шығатыны f `c=0.
Геометриялық мағанасы: у = f (x) функциясы графигінің (с; f (с) ) нүктесіндегі жанамасы абцисса осіне параллель болады.
Ролль теоремасы
Егер : у = f (x) функциясы:
* а,в кесіндісінде үзіліссіз
* а,винтервалында дифференциялданатын,
* кесіндінің ұштарында өзара тең мәндер қабылдайтын, яғни fa=fb, болса, онда ең болмағанда бір с (а,в) нүктесі табылып f `c 0
болады.

Дәлелдеуі: Теорема шарты бойынша : у = f (x) функциясы а,в кесіндісінде үзіліссіз, демек, Вейрштрасс теоремасы бойынша кесіндінің қандай болса да бір нүктесінде ол өзінің ең үлкен (ең кіші) мәнін қабылдайды.
M=maxх ∈ (а, в)f (x)
m=minх ∈ (а, в)f (x)
болсын, сонда барлық х ∈ (а, в) үшін m= f (x)=M. Мұнда екі жағдай болуы мүмкін:
1) m = M , онда f (x) = const демек, кез келген х ∈ (а, в) нүктесі үшін f `c=0, яғни теорема дұрыс.
2) Егер M m , болса , онда fb-f(a) болғандықтан, бұл мәндерінің ең болмағанда біреуін, мысалы, М мәнін f (x) функциясы а,в кесіндісінің ішкі нүктесінде қабылдайды. Демек, с ∈ (а, в) нүктесі табылып, f c=М болады. Олай болса Ферма теоремасы бойынша f `c=0. Сонымен теорема дәлелденді.
Геометриялық мағанасы: егер у = f (x) қисығының шеткі ординаталары бірдей болса, қисық бойындағы ең болмағанда бір нүктеде жанама абцисса параллель болады.
Теоремадан мынадай маңызды салдарлық тұжырым шығады: дифференциалданатын функцияның кез келген екі нақты түбірінің арасында оның туындысының ең болмағанда бір түбірі болады.

2. Лагранж теоремасы.
Егер у = f (x) функциясы:
* а,в кесіндісінде үзіліссіз
* а,винтервалында дифференциялданатын , ақырлы туындысы
* бар болса, онда

fb-f(a)b-a = f'(c)
теңдігі орындалатындай ең болмағанда бір с ∈ (а, в) нүктесі табылады.
Лагранж теоремасын дәлелдеу үшін қосымша Fx=fx-λx функциясын енгізе отырып, осыған ұқсас схемамен дәлелдеу жолын пайдаланады. Лагранж теоремасы Коши теоремасының дербес жағдайы болып табылатыны айқын. Шынында да, ақырлы өсімшелердің жалпыланған формуласынан ақырлы өсімшелер формуласын алу үшін g(x)=x деп алу жеткілікті. Сондықтан Лагранж теоремасының дәлелдемесін келтірмейміз.
Коши формуласы және Лагранж формуласы тек a b , болғанда ғана дұрыс болып қоймай a b болғанда да дұрыс болып қала береді.
Геометриялық мағанасы: у = f (x) графигі бойында А ( а; f ( a)) және
B ( b; f ( b)) нүктелері арасынан C ( c; f ( c)) , а сb нүктесі табылып, графикке осы нүктедегі жанама АВ хордасына параллель болады.
fb-f(a) = f ` (c) b-a , а ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.