Гидродинамика

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 5 бет
Таңдаулыға:

№8 Гидродинамика

Гидродинамика - сұйықтың қозғалыс заңдылықтарын және осы заңдарды тұрмыстығы әртүрлi мақсаттарға пайдалану мүмкiншiлiктерiн қарастырумен айналысады.

Сұйық дегенiмiз - алып отырған көлемiн бос орынсыз және үзiлiссiз толтырып туратын бөлшектер жиынығы.

Сұйық бөлшектерi - қарастырып отырған сұйықтың көлемiн салыстырғанда аз сұйық бөлiгi, бiрақ сұйық молекулаларының көлемiнен салыстырсақ ол үлкен болады. Сұйық бөлшегiне молекулалар соншалықты көп болғандықтан, бөлшек көлемiндегi сұйықты бiртектi сұйық немесе континуум деп атаумызға болады.

Сұйық қозғалысын зерттеу әдiстерi

Сұйық қозғалысын зерттеуде екi түрлi бiр-бiрiне ұқсамайтын аналитикалық әдiстер бар: Олар Ланграж және Эйлер әдiсi.

Лангранж әдісі. Қозғалыстағы сұйықтан К контурымен белгіленетін, кез келеген облысты бөлiп аламыз.

Қозғалмайтын Оx және Оz координат остерiн белгiлеймiз. Қозғалыста тұрған бiрқатар М ₁ ; М ₂ ; М ₃ сұйық бөлшектерiн қарастырамыз. Олар уақыттың басталған мезетiне қарастырып отырған облыстың шекарасында орналасқан.

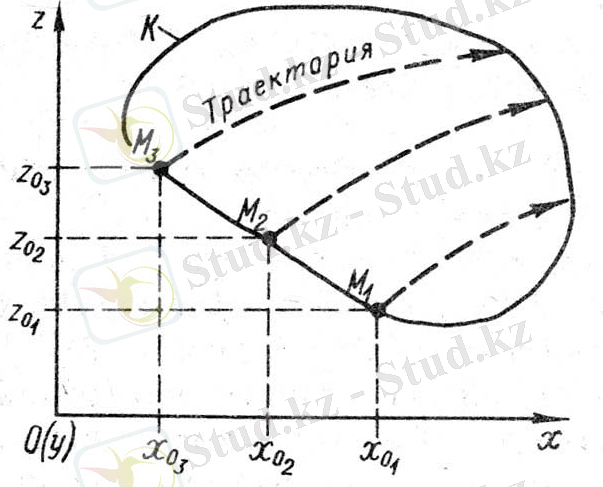
1%20лек%2015

1. 17 сурет

Бұл сұйық бөлшектерiнiң бастапқы координаттарын x ₀ , z ₀ , мен белгiлеймiз. Әрбiр М сұйық бөлшегi үшiн бiзге төмендiгi байланыстар белгiлi деп есептеймiз.

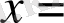
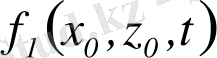
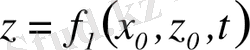
Онда осы байланыстарды пайдалана отырып әрбiр белгiленген сұйық бөлшектерiнiң траекториясын тұрғызуға болады. Одан ары 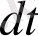уақыты аралығында осы траекториядағы жүрiп етiлген 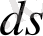жолды табуымызға болады. Көрiп отырғанымыздай, бiз t уақытта қозғалыста болып, өз траекториясымен қарастырып отырған облысты толығымен жүрiп өтетiн сұйықтың бөлшегiн бақылаймыз.

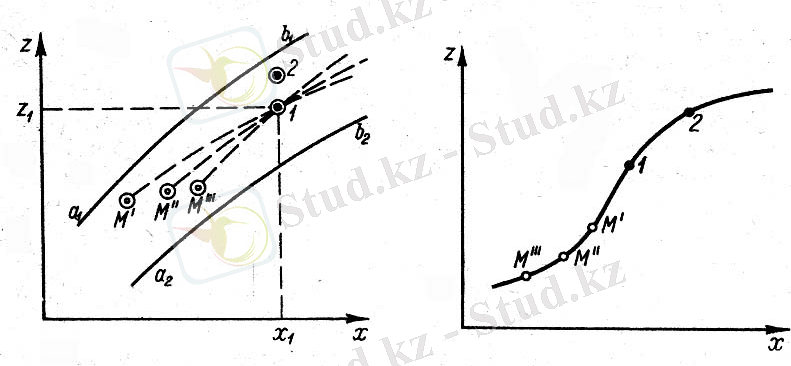
2. Эйлер әдiсi. Тағы да қозғалыстағы сұйық алып тұрған К облысын аламыз. Эйлер бойынша, бiз ендi сұйық бөлшектерiнiң қозғалысын қадағаламаймыз, траекториясын да қарастырмаймыз. Эйлердiң ұсынуы бойынша қарастырып отырған қозғалмайтын кеңiстiкте 1, 2, 3 нүктелерiн белгiлеймiз. Бұл нүктелердiң үстiмен сұйық ағып өткенде олар қозғалыссыз болады. Мұндағы х және z мәндерi сұйық бөлшектерiнiң ағымдағы координаттары емес, олар кеңестiктегi қозғалмайтын нүктелердiң координаттары.

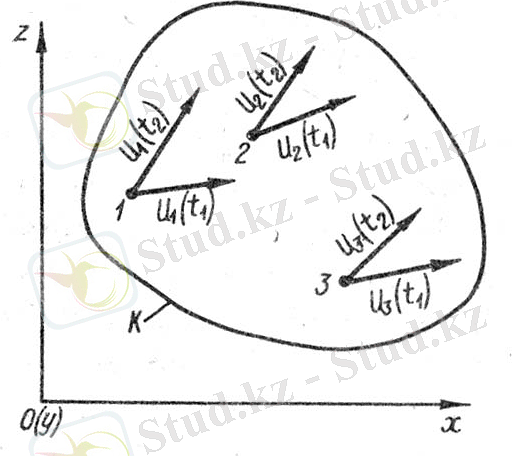
1%20лек%2016

1. 18 сурет

t ₁ уақыт мезетiн қарастырамыз. Бұл (t ₁ ) уақытта 1 нүктеде u ₁ (t ₁ ) жылдамдығы бар сұйықты бөлiгi болады, дәл осы уақытта 2 нүктеде u ₂ (t ₁ ) жылдамдығына, 3 нүктеде u ₃ (t) жылдамжығын бiлемiз.

Келесi (t ₂ ) уақыт месетiнде 1, 2, 3, нүктелерiнде тиiсiнше u ₁ (t ₂ ) ; u ₂ (t ₂ ) ; u ₃ (t ₂ ) жылдамжықтарын аламыз.

Көрiп отырғанымыздай, Эйлер бойынша, су ағыны алынған бiр уақытта кеңестiктегi қозғалмайтын нүктелерге байланысты жылдамдық векторлық өрiсiмен суреттеледi.

Лангранж әдiсi оның күрделi болуына байланысты гидравлика көп қолданылмайды. Келешекте бiз негiзiнен Эйлер әдiсiн қолданамыз.

Сұйық қозғалысының түрлерi

Гидравликадағы басты есеп - қозғалысты сыйпаттайтын негiзгi мәндердiң арасындағы байланыстарды: олар сұйық қозғалысы кезiндегi пайда болатын қозғалыстың жылдамдықтары, терендiк пен қысым арасындағы байланыстары анықтау болып табылады.

Қозғалыстағы сұйықта пайда болатын қысымды гидродинамика қысымы деймiз. Сұйық бөлшектерiнiң қозғалыс жылдамдығын жергiлiктi жылдамдық деймiз.

Жалпы алғанда гидродинамикалық қысым және сұйық бөлшектерiнiң қозғалысы қозғалып тұрған сұйықтың әрбiр нүктесiн де өзгерiп тұрады, яғни 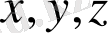координаттарының функциясы болады. және де бұлардың мәндерi уақытқа байланысты өзгерiп, уақыт 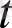-тың де функциясы болуы мүмкiн.

Осыған байланыста сұйық қозғалысты екi түрi болады. Қалыптасқан және қалыптаспаған.

Сұйықтың қалыптасқан қозғалысы дегенiмiз - кез келген нүктедiгi гидродинамикалық қысым және қозғалыс жылдамдығы уақытқа байланысты өзгермейдi, тек ғана қарастырып отырған нүктенiң сұйық ағыныптағы орнына байланысты болып, осы координаттардың функциясына айналады.

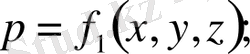
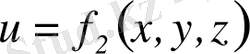
Сұйық қалыптаспаған қозғалысы дегенiмiз - гидродинамикалық қысым мен қозғалыс жылдамдығы сұйық ағанының кез келген нүктесiнде тек ғана координаттардың емес, сонымен бiрге уақыттың функциясы болады.

1%20лек%2017

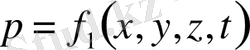
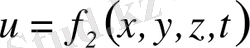
1. 19 сурет

Сұйықтың бөлшегiнiң қозғалу траекториясы,

ағын сызығы, ағын құбыршасы, қарапайым толтырма,

сұйық ағыны тұралы түсiнiк

Жоғарыдан келтiрiлген функциясындағы айнымалы мәндердiң көп болуына байланысты. Оларды шешу өте күрделi есеп болып табылады. Сондықтан келтiрiлген функцияларды шешудi оңайлату үшiн тұтқырлығы болмайтын идеалды сұйық түсiнiгiн пайдаланамыз, сондай-ақ сұйық ағыны әр түрлi жылдамдықпен қозғалатын қарапайым шаптырмалардан құралады деп есептелiнетiн шаптырмалы қозғалыс моделiн кiргiземiз. Қапарайым шаптырмалар үшiн алынған гидродинамиканың негiзгi теңдеуi идеалды сұйықтың толық ағысына да қолданылуы мүмкiн. Бұл модельдi нақты сұйық қозғалысын зерттеуге қолданған кезде қосымша тәжiребе жолымен алынған үйкелiс күшiн ескеретiн коэфиценттер енгiзiледi.

Сұйықтың шаптырмалы қозғалыс моделiн зерттемес бұрын сұйық бөлшегiнiң қозғалу траекториясы - кеңiстiктегi белгілi бiр сұйық бөлшегiнiң қозғалысының iзi.

Сұйықтан бiр а нүктесiн алып, осы нүкте арқылы өтетiн барлық сұйық бөлшектерiнiң а нүктесiндегi қозғалыстарының қорытынды бағыт пен жылдамдығының 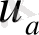векторын тұрғызамыз. Осы вектордың бойынан а нүктесiнен 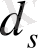өте кiшкентай қашықтықтан 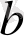нүктесiн аламыз. Бұл нүктеде де осы арқылы барлық өтетiн сұйық бөлшегiнiң жылдамдығы мен бағытына қорытындысы саналатын 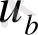- жылдамдық векторын саламыз. Осындай 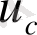жылдамдық векторының 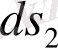с нүктесiнде де саламыз. Егер 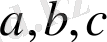нүктелерi аралығындағы болатын 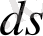қашықтықты нолге дейiн азайтатын болсақ, онда шектiң мәнiнде 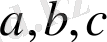кесiндiлер құрағы 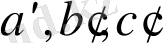қисығына айналады. Бұны ағын сызығы деймiз.

1%20лек%2019

1. 20 сурет

Қалыптасқан қозғалыс жағдайында ағын сызығына уақыт бойынша өзгермейдi, сондықтан олар бөлшек траекториясын дәлмедал келедi.

Ағын құбыршасы. Егер тұйықталған контурдың барлық нүктелерi арқылы ағын сызығын өткiзетiн болсақ, онда соңғылары арасында саңлауы жоқ құбырша түзіледi - мұны ағын құбыршасы деймiз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.