Гидростатиканың негізгі теңдеуі мен қысым түрлері: абсолютті, манометрлік және вакуумдық құбылыстар


Гидростатиканың негізгі теңдеуі
Абсолютті және манометрлік қысым, Ваккум
Сабақ жоспары:
1. Сабақ мақсаты мен міндеті.
Гидростатиканың негізгі теңдеуімен қысымдардың айырмасын есептеу,
Абсолютті және манометрлік қысым, Ваккумдық құбылыстардың қасйетін қарастыру
- Қарастыратын сұрақтар.
- гидростатикалық қысымның негізгі теңдеуінің шығу тегі.
- Теңдеулер байланысын зерттеу.
Э. Эйлер жасаған сұйықтың тепе-тендiк
қалпының негiзгi дифференциалды теңдеуi
Қандай да бiр (ауырлық күшi де болмауы мүмкiн) сыртқы көлемдiк күш әсер ететiн тыныштық қалпындағы сұйықты аламыз (1. 5 сурет) .
Оx, Оy, Оz өсiне сәйкес межейiктi көлемдiк күш Ф-тың проекцияларын Ф х , Ф у , Ф z - тi белгiлеймiз.
Оx, Оy осьтерiнiң бағытымен тiктөртбұрыш 1-2-3-4 параллепипедтен тұратын тыныштықтағы сұйықтың элементарлық көлемiн бөлiп аламыз. Параллепипедтiң қабырғалары dх және dz сондай ақ сызбаның бетiне перпендикуляр болатын dy мәндерiн өте кiшкентай деп есептеймiз.
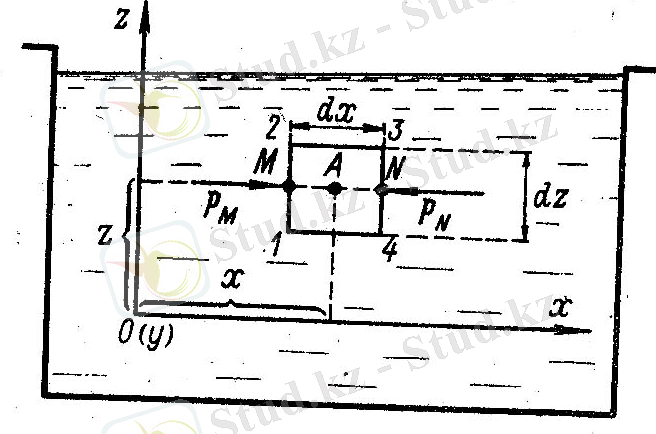
1. 5 сурет
Параллелепипедтiң ортасынан
х, у,
және
z
координатолары бар
А
нүктесiн аламыз. Бұл нүктедегi қысымды
p
-деп белгiлеймiз. Осы
А
нүктесi арқылы
О
x
осiне параллел
МN
сызығын жүргiзе отырып, осының бойында гидростатикалық қысым үздiксiз өзгерiп отырады деп есептеймiз.
МN
сызығын ұзына бойғы бiрлiгiне келетiн гидростатикалық қысымның өзгерiсiн жеке туынды
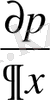 , арқылы қарастырайық.
, арқылы қарастырайық.
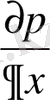 , пайдалана отырып
М
және
N
нүктесiндегi қысымды өрнектеймiз.
, пайдалана отырып
М
және
N
нүктесiндегi қысымды өрнектеймiз.
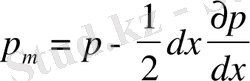 (1. 14)
(1. 14)
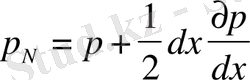 (1. 15)
(1. 15)
мұнда оң жақтағы теңдiктiң екiншi құраушысы
p
қысымның
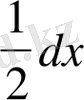 ұзындықтағы өзгеруiн көрсетедi.
ұзындықтағы өзгеруiн көрсетедi.
Одан әрi былай ойластырамыз:
а) Элементарлық параллелепипедке әсер ететiн барлық күштердi анықтаймыз.
б) Бұл күштердi О x осiне проекциялаймыз. Қарастырып отырған параллелепипед тыныштық жағдайында тұрғандықтан, барлық табылған күштердiң проекцияларының суммасын нольге теңестiремiз. Нәтижесiнде бiрiншi дифференциалды теңдеу аламыз.
в) 2-ий және 3-ий дифференциалдық теңдеудi алу үшiн параллепипедке әсер ететiн барлық күштердi тиiсiнше О y және О z осьтерiне проекциялаймыз.
Айтылған жолмен жүрiп тек 1-шi дифференциалдық теңдеудi шығарамыз.
1-2-3-4 параллелепипедке әсер етушi күштер:
а) көлемдiк күш
Ф (dx dy dz)
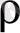 (1. 16)
(1. 16)
мұнда
(dx dy dz)
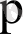 -
1-2-3-4 параллелепипедтi құрап тұрған сұйықтың массасы. Бұл күштiң О
x
осiне проекциясы
-
1-2-3-4 параллелепипедтi құрап тұрған сұйықтың массасы. Бұл күштiң О
x
осiне проекциясы
Ф
х
(dx dy dz)
 (1. 17)
(1. 17)
б) беттiк күштер: 1-4 және 2-3 қырларындағы қысым күшiнiң айырмашылығының О x осiне прекциясы нольге тең; 1-2 және 3-4 қырларындағы қысым күшiнiң айырмашылығы мынаған тең:
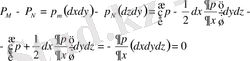 (1. 18)
(1. 18)
 2. Барлық күштердi О
x
осiн прекциясының қосындысы нольге тең.
2. Барлық күштердi О
x
осiн прекциясының қосындысы нольге тең.
Ф
х
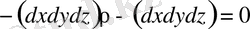 (1. 19)
(1. 19)
Бiрiншi теңдеу осылай көрiнiс табылады. Қалған екеуiн бiрiншiдей етiп табамыз. Табылған үш дифференциалдық теңдеу соңына төмендегiдей болады (сұйықтың массасының бiрлiгiне келтiргенде) .
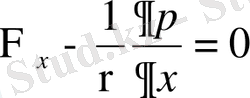
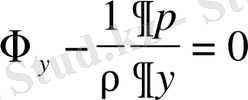
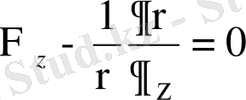 (1. 20)
(1. 20)
Бұл теңдеулердi Э. Эйлер бiрiншi рет 1755 ж. шығарған.
Тыныштықтың жағдайындағы сұйықтың
гидростатикалық қысымының теңдеуi
(1. 20) дифференциалдық теңдеудiң 1-шiсiн dx, екiншiсiн dy 3-шiсiн dz көбейтемiз. Сонан соң бұл теңдеулердiң оң жағын және сол жағын бiр-бiрiне қосамыз.
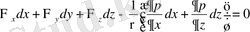 (1. 21)
(1. 21)
Кез-келген нүктедегi қысым тек координаттың ғана функциясы болғандықтан:
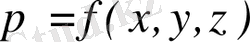 (1. 22)
(1. 22)
(1. 21) теңдiктегi жақшаның iшiндегi өрнектер p -ның толық дифференциалы деп айтуымызға болады, немесе ол dp тең. Сондық (1. 21) қайта мына түрде жазамыз:
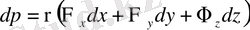 (1. 23)
(1. 23)
(1. 23) -шы теңдеудiң оң жағында жақшаның iшiнде тұрған өрнек те координатаға байланысы бар
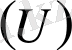 функциясының толық дифференциалы болып табылады. Сонда
функциясының толық дифференциалы болып табылады. Сонда
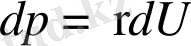 (1. 24)
(1. 24)
мұнда
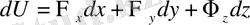
(1. 24) -шы теңдiктен интеграл алатын болсақ
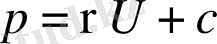 (1. 25)
(1. 25)
мұнда С- интегралдау тұрақтысы.
С мәнiн анықтау үшiн p және U мәндері белгілі сұйықтың нүктесін қарастырайық
p= p 0 ; U = U 0 (1. 26)
Бұл нүкте үшін (1. 25) былай жазылады:
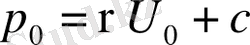 (1. 27)
(1. 27)
бұдан
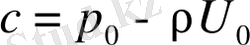 (1. 28)
(1. 28)
(1. 28) -тi (1. 25) -шi теңдеуге қойып, мынаны аламыз
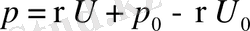 (1. 29)
(1. 29)
немесе
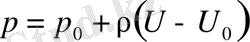 (1. 30)
(1. 30)
(1. 30) теңдеу
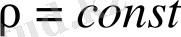 - тұрақты болған кездегi нүктедегi кез келген көлемдiк күштер жүйесiнiң әсерiнен пайда болатын қысымды бередi.
- тұрақты болған кездегi нүктедегi кез келген көлемдiк күштер жүйесiнiң әсерiнен пайда болатын қысымды бередi.
гидростатикалық қысымының теңдеуi .
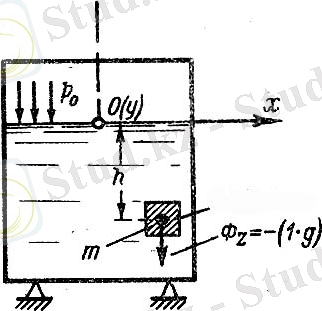
Тек ғана бiр көлемде күш - ауырлық күшi ауырлық күшi түсiп тұрған сұйықты қарастырамыз (1. 6 сурет) .
Суреттiң iшiнде сұйығы бар жабық ыдысты қарастырамыз. Сыртқы беттiк қысымды (немесе сұйықтың еркiн бетiне түсетiн қысымды) Р 0 -деп белгiлеймiз. Суретте көрсетiлгендей ординаталар осiн ашып, m нүктесiн айнала бiрлiк массасы бар сұйықты бөлiп аламыз. Бұл алынған масса бiрлiгiне көлемдiк Ф күшi әсер етедi.
1 масса бірлігі
1. 6 сурет
Егер сұйыққа әсер ететiн көлемдiк күштер тек ауырлық күшiнен тұратын болса, онда:
Ф
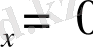 :
:
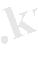 Ф
Ф
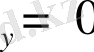 Ф
Ф
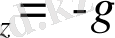 (1. 31)
(1. 31)
где g - еркiн түсу үдейi; Ф х Ф у Ф z - Ф күшiнiң координата остерiне проекциясы.
(1. 24) өрнегін еске түсіреміз
dp=
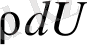 (1. 32)
(1. 32)
мұндағы dU бiздiң жағдайымызда.
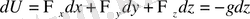 (1. 33)
(1. 33)
1. 33 өрнектi 1. 32-ге қоямыз.
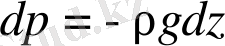 : (1. 34)
: (1. 34)
Интеграл алатын болсақ.
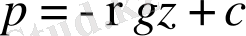 (1. 35)
(1. 35)
немесе
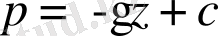 (1. 36)
(1. 36)
Егер (1, 35) өрнектi:
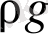 бөлсек онда (1. 37) өрнектi аламыз.
бөлсек онда (1. 37) өрнектi аламыз.
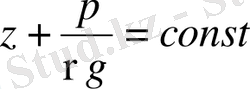 (1. 37)
(1. 37)
Тыныштықта тұрған сұйықтың екi нүктесi үшiн (1. 37) келесі түрде жазылады:
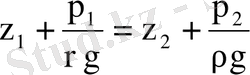 (1. 38)
(1. 38)
Бұл алынған теңдеу гидростатиканың гидростатиканың негiзгi теңдеуi.
(1. 36) өрнектегi С-интеграл тұрақтысы. С-ны анықтау үшiн сұйықтың еркiн бетiнен бiр нүкте аламыз. Бұл жерде
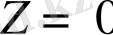 ал
ал
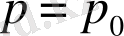 (1. 6 суреттi), соңғы (1. 36) өрнек бұл нүкте үшiн былай жазылады.
(1. 6 суреттi), соңғы (1. 36) өрнек бұл нүкте үшiн былай жазылады.
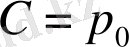 :
:
Сондықтан (1. 36) орнына былай жазамыз.
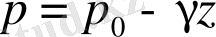 (1. 39)
(1. 39)
 -нүктесiнiң судың бетiнен төмен түсуын
h
белгiлейтiн болсақ.
-нүктесiнiң судың бетiнен төмен түсуын
h
белгiлейтiн болсақ.
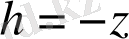 (1. 40)
(1. 40)
Сонда (1. 39) өрнектi былай жазуға болады.
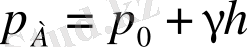 (1. 41)
(1. 41)
мұнда
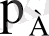 -қарастырылып отырған нүктедегi абсолюттiк қысым,
-қарастырылып отырған нүктедегi абсолюттiк қысым,
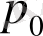 -су бетiндегi сыртқы қысым. (10)
-су бетiндегi сыртқы қысым. (10)
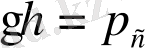 -деп белгiлейтiн болсақ, ол салмақтың қысымы деп аталады.
-деп белгiлейтiн болсақ, ол салмақтың қысымы деп аталады.
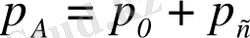 (1. 42)
(1. 42)
(1. 42) өрнектен байқайтынымыз нүктедегi абсолюттiк қысым су бетiне түскен сыртқы күш пен нүктедегi салмақ қысымына тең.
Егер ыдыстың бетi ашық болса, онда
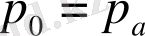 - атмосфералық қиымға тең. Бұл жағдайда (1. 42) орнына
- атмосфералық қиымға тең. Бұл жағдайда (1. 42) орнына
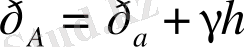 (1. 43)
(1. 43)
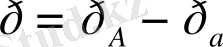 (1. 44)
(1. 44)
нүктедегi абсолюттiк қысымының атмосфералық қысымнан артық бөлiгiн артылған қысым (р) немесе атмосфералықтан жоғары қысым деп белгiлеймiз.
а) сонда бетi жабық ыдыстар үшiн (11) формула.
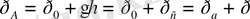 (1. 45)
(1. 45)
б) бетi ашықтар ыдыстар үшiн:
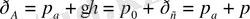 (1. 46)
(1. 46)
бұдан байқайтынымыз ашық ыдыстар үшiн салмақтың және артылған қысым деген түсiнiк бiр-бiрiне сәйкес келедi.
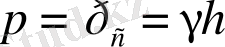 (1. 47)
(1. 47)
ал жабық ыдыстар үшiн
р
и
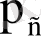 әр түрлi мәнi ие.
әр түрлi мәнi ие.
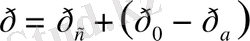 (1. 48)
(1. 48)
Өзiмiз көрiп отырғандай, бес түрлi қысымның бiлгiлерi бар. Олар
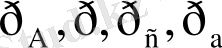 және
және
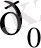 . р- артылған гидростатикалық қысым (атмосфералық жоғары) немесе манометрiне қысым деп атайды.
. р- артылған гидростатикалық қысым (атмосфералық жоғары) немесе манометрiне қысым деп атайды.
Пьезометрлік биiктiк
Пьезомерлiк сөзi гректiң “пьезо” қысым “өлшеу” деген сөздерiнен шыққан. Пьезометрлiк биiктiк дегенiмiз артылған қысымының р меншiктi салмағы γ қатынасы.
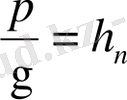 (1. 49)
(1. 49)
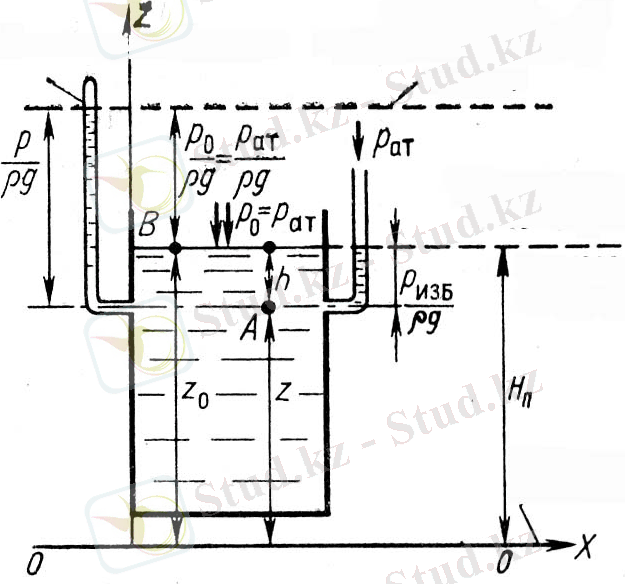
1. 7 сурет
Салыстыру
жазықтығы
Пезометриялық
арынның жазықтығы
Гидростатикалық
арын жазықтығы
Абсолюттік вакуум
Егер жабық ыдыстан (1. 7 сурет) А нүктесiн алып оған ашық трубка қоссақ, онда трубкадағы сұйық белгiлi бiр денгейге h көтерiледi. Мұны манометрлiк немесе пьезометрлiк қысым дейдi. Ыдыстағы Р 0 қысым атмосфералық Р а кем болса, манометрлiк қысым терiс болады. Оны вакуум дейдi.
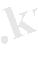 h
вак
=
h
вак
=
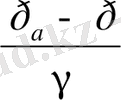 (1. 50)
(1. 50)
Жабық резервуардағы тыныштық қалыптағы сұйықты қарастырамыз. Бұл ыдыстағы су бетiндегi қысым
р
0
. Бұл резервардың iшiнен екi
А
және
В
нүктесiн аламыз да пьезометр орнатамыз. Бұларды салыстыру үшiн
ОО
салыстыру жазықтығын саламыз.
А
және
В
нүктелерiнiң осы жарықтықтан қашықтығы z
A
және z
В
; Егер бұл нүктедегi гидростатикалық қысымды р
A
және р
В
деп белгiлейтiн болсақ онда пьезометрлiк биiктiктер
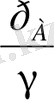 және
және
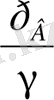 болады.
болады.
Гидростатиканың негiзгi теңдеуi бойынша
 H
Г
H
Г
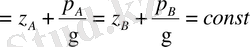 (1. 51)
(1. 51)
H
Г
-
гидростатикалық немесе пьезометрлік арын дейдi. Егер осы резервуарға
А
нүктесiне дейiн төбесi жабық, демек ондағы қысым 0-ге тең болатын түтiкшенi төңкеретiн болсақ, онда сұйық
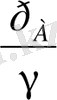 биiктiкке көтерiледi. шыну
р
А
-
А нүктесiндей толық гидростатикалық қысым. Бұл биiктiк - келтiрiлген биiктiк деп атайды.
биiктiкке көтерiледi. шыну
р
А
-
А нүктесiндей толық гидростатикалық қысым. Бұл биiктiк - келтiрiлген биiктiк деп атайды.
Гидростатикалық негiзгi теңдеудiң тыныштықтағы сұйықтың екі нүктесiне қолданатын болсақ, онда
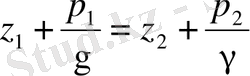 (1. 52)
(1. 52)
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz