Mathcad-та программалауды оқыту әдістемесі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 65 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БIЛIМ ЖӘНЕ ҒЫЛЫМ МИНИСТРЛIГI
Қазақ мемлекеттiк қыздар педагогика институты
Физика-математика факультетi
Информатика және қолданбалы математика кафедрасы
Дипломдық жұмыс
Тақырыбы:«Mathcad-та программалауды оқыту»
Қорғауға жіберілді
" " 2008ж.
кафедра меңгерушісі
тех. ғ. к., доцент
Салғараева Г. И.
Орындаған:
050111-информатика мамандығының 4-курс студенті Омарова Бағдат
Ғылыми жетекші: пед. ғ. к., доцент
Керімбаев Н. Н.
АЛМАТЫ 2008
Мазмұны
Кіріспе . . . 3
І тарау. Mathcad программалау ортасындағы операторлар
1. 1. Математикалық формулаларды енгізу және формулалық редактормен жұмыс істеу әдістері . . . 4
1. 2. Меншіктеу және шығару операциялары . . . 7
1. 3. Mathcad сызықтық және сызықтық емес теңдеулерді программалау есептерін шешу . . . 19
1. 4. Массивтердің векторларды және матрицаларды есептеу операторларымен жұмыс істеу . . . 22
ІІ тарау. Mathcad-ты оқытуға арналған орта мектепте оқытудағы практикалық және зертханалық жұмыстар.
2. 1 Қолданушыға операторларды түсіндіру әдістері . . . 33
2. 2 Mathcad-тан тапсырмалар жүйесі . . . 45
2. 3 Mathcad-та программалауға арналған зертханалық жұмыстар . . . 52
Қорытынды . . . 58
Қолданылған әдебиеттер. . . . 59
Қосымша . . . 60
КІРІСПЕ
Mathcad ғылымның, техниканың және білімнің кез-келген саласын қамтамасыз етеді.
Қазіргі таңда Mathcad-тың алуан түрлері математикалық бағыттаушы әмбебап жүйесі болып табылады. Ол сандық және аналитикалық есептеуден басқа танымал мәтіндік редакторлерде немесе электрондық кестелерде қиындықпен берілетін күрделі көркемдеуші тапсырмаларды шешуге мүмкінідк береді. Mathcad-тың көмегімен мақалаларды, кітаптарды, диссертацияларды, ғылым саласында есеп берулерді, дипломдық, курстық проектілерді сапалы мәтіндердің түрлі стильдерімен ғана емес, сонымен қатар күрделі математикалық формулалардың жүзеге асырылған жиынтығын есептеудің таңдаулы көрсетілген нәтижесін және сансыз көп мысалдарын дайындауға мүмкіндік береді.
Mathcad-тың жаңа түрінде құжатты түрлі түспен безендірілуінің тиімді жолы жылжымалы графиктерді құру және дыбыстық сүйемелдеу мүмкіндіктері енгізілген. Мұндағы мәтіндік формулалар және графикалық редакторлар жүйе ядросының есептеу потенциялымен біріктірілген. Сонымен қатар күрделі есептерді шешуге арналған басқада математикалық және графикалық жүйелерді біріктіру мүмкіндіктері қаралған. Бұл жүйенің аты интегралдық жүйе. Жалпы айтқанда бұл жүйе басқада математикалық, графикалық және офистік жүйелердің интеграциясын қамтамасыз етеді. Mathcad-тың көмегімен мәтіндік редактормен, математикалық формулаларды енгізу және формулалық редактормен жұмыс жасауға, меншіктеу және шығару амалдарын математимкалық операторлармен символрадың шаблондарымен қалдануға, математикалық функцияларды есептеуге болады.
Сонымен қатар жүйенің графикалық мүмкіндіктерін ұтымды пайдалану және көркемділік жақтарын математикалық улгілеу әдістерінде кеңінен қолдануға анимациялауға, бейнелеу кадырын құруға, дифференциялдық теңдеулерді шешуге болады.
І. MATHCAD ПРОГРАММАЛАУ ОРТАСЫНДАҒЫ ОПЕРАТОРЛАР
1. 1. Математикалық формулаларды енгізу және формулалық редактормен жұмыс істеу әдістері
Mathcad жүйесі өзінде үш редакторды интегралдайды: формулалық, тексттік және графикалық. Формулалық редакторды іске қосу үшін редакторлеу терезесінде тышқанның оң жақ батырмасын шерту жеткілікті. Кішкентай қызыл крестик түріндегі енгізу курсоры осы орынға алып келінеді. Оны ауыстыру курсорының пернелері арқылы ауыстыруға болады. Енгізу курсорын қара қиғаш стрелка түріндегі тышқан көрсеткішімен шатастыруға болмайды.
Енгізу курсоры формулулар жиынтығы - есептеу блоктарын бастауға болатын орынды көрсетеді. Енгізу курсоры орналасқан орнына байланысты өзінің пішінін өзгертеді. Енгізу облысында ол енгізу бағытын және орнын көрсететін көк бұрышқа айналады. Кеңейту үшін қамтылған бұрыш облысында Пробел пернесін қолдануға болады.
Арифметикалық формулуларды есептеу және оларды редакторлеу мысалдары. 2+3 қосындысының түбір астындағы 5 санына қатынасын есептейтін мысалды қарастырайық. Алдымен 2+3 символын енгіземіз. Мұның формулалық блогы 2. 1-суретте көрсетілген. Енгізу бұрышы соңғы операндты қамтып тұрғанына назар аударыңыз.
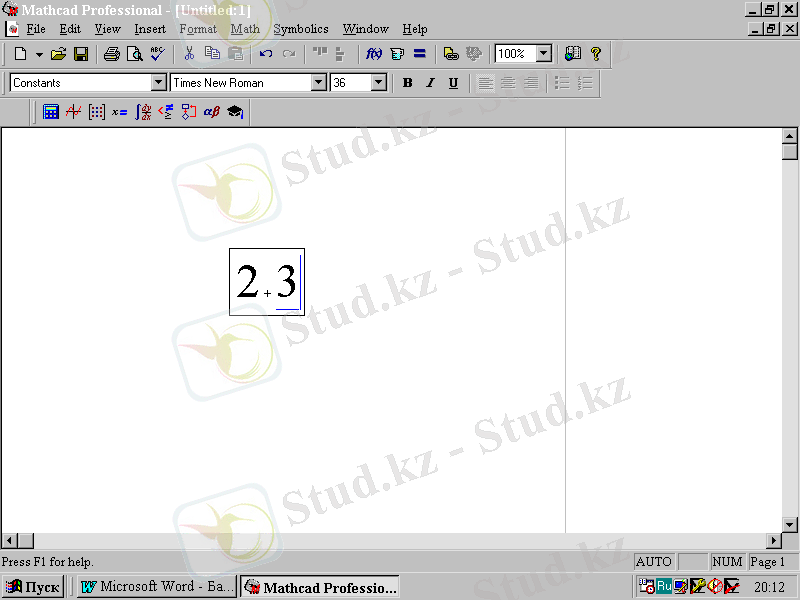 2. 1-сурет.
Формулалық блокты жасау және оған 2+3 қосындысын енгізу
2. 1-сурет.
Формулалық блокты жасау және оған 2+3 қосындысын енгізу
Енді бөлу белгісін енгізу керек. Егер мұны бірден орындайтын болсақ, онда белгі барлық қосындыға қатысты емес, тек соңғы операнд 3 санына ғана қатысты болады. Ол үшін пробел белгісін басу жеткілікті. Шыққан нәтиже 2. 2-суретте көрсетілген.
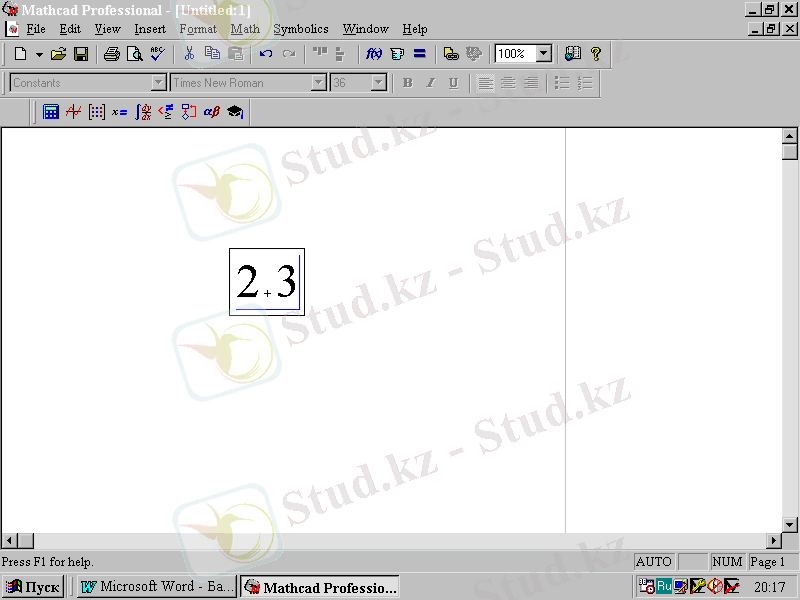 2. 2-сурет.
Барлық қосындыны енгізу курсорымен белгілеу
2. 2-сурет.
Барлық қосындыны енгізу курсорымен белгілеу
Енді бөлу белгісін / белгісіндегі пернені басу арқылы енгізуге болады. Формулалық блок 2. 3-суретте көрсетілген. Сызықша түріндегі бөлу белгісі автоматты түрде қосынды астындағы ұзын көлденең сызықша пайда болғанын, ал оның астында енгізу курсорымен қамтылған қара квадрат түріндегі бөлшек бөлгішін енгізу орны шығады.
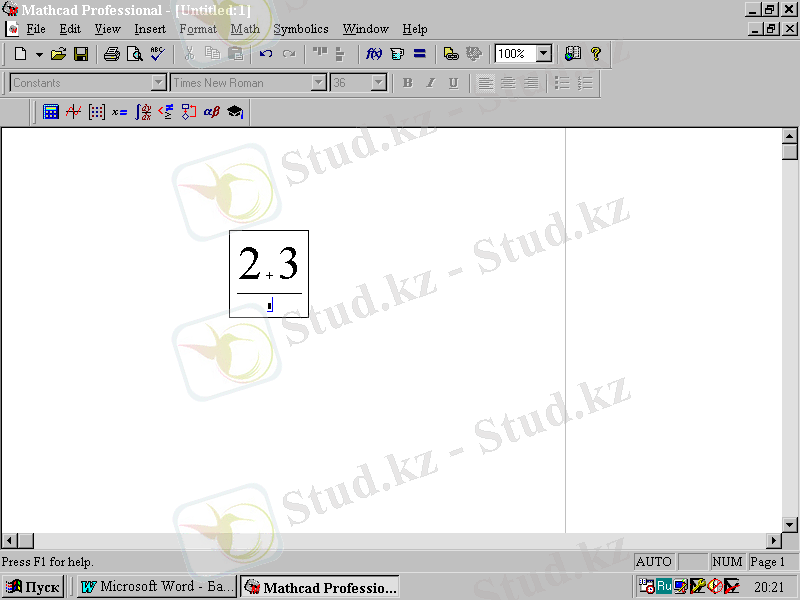 2. 3-сурет.
Бөлу белгісін енгізгеннен кейінгі
2. 3-сурет.
Бөлу белгісін енгізгеннен кейінгі
формулалық блок
Келесі кезең - квадрат түбір белгісін енгізу. Жаңадан үйреніп жүрген қолданушы бұл белгіні Calculate арифметикалық операциясына арналған математикалық белгілер палитрасын қолдану арқылы енгізеді. Мұндай енгізу үшін квадрат түбір белгісінде тышқанды шерту жеткілікті немесе кері сызықша \ белгісіндегі пернені басу жеткілікті. Алынған формулалық блок 2. 4-суретте көрсетілген.
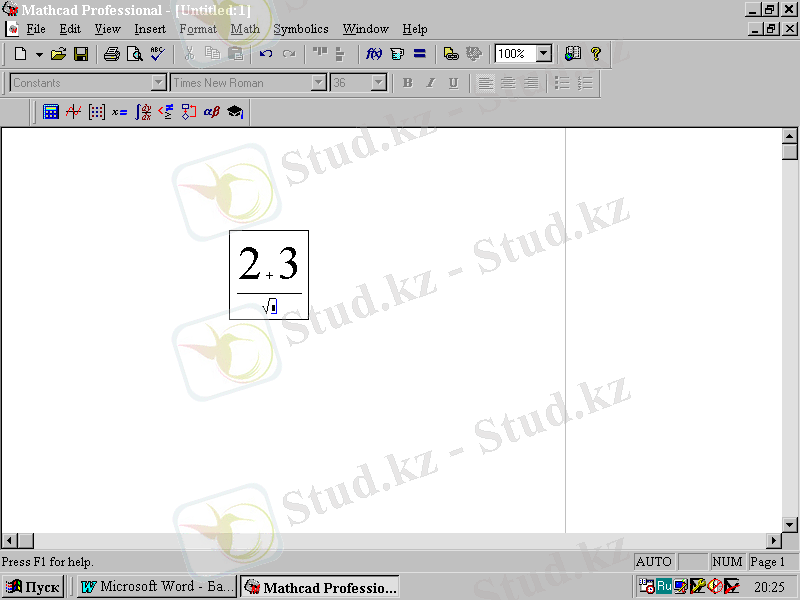 2. 4-сурет.
Квадрат түбір белгісін енгізгеннен кейінгі формулалық блок
2. 4-сурет.
Квадрат түбір белгісін енгізгеннен кейінгі формулалық блок
Келесі кезең түбір астына 5 санын енгізуді құрастыру. Ол үшін 5 пернесін басу жеткілікті. Формулалық блок 2. 5-суретте көрсетілген.
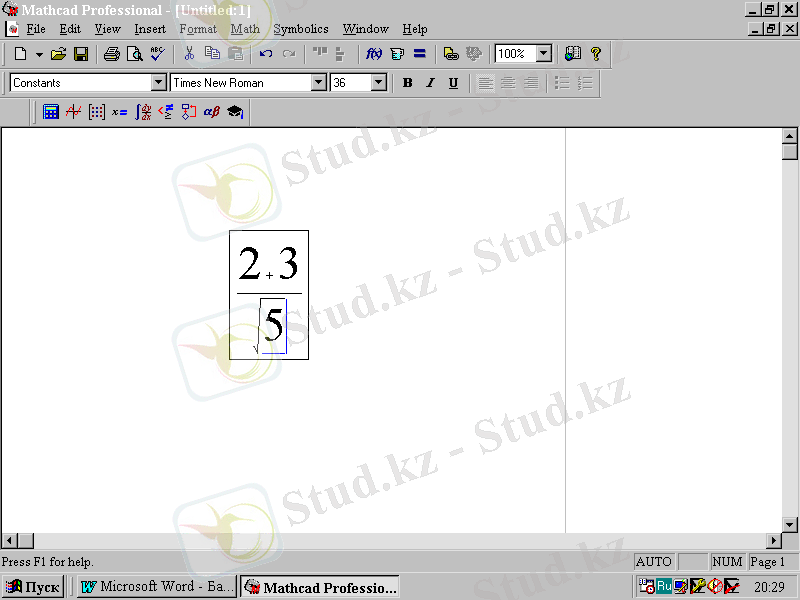 2. 5-сурет.
Берілген теңдеудің формулалық блогы
2. 5-сурет.
Берілген теңдеудің формулалық блогы
Формула толығымен енгізілді, ендігі қалғаны - есептеудің нәтижесін көру. Ол үшін формула соңына шығару операторы - теңдік белгісін = қою керек. Бірақ оны бірден қоюға болмайды, өйткені шығару белгісі соңғы операторға орнатылған. Алдымен барлық формуланы белгілеу керек. Ол үшін Пробел пернесін басқанда, барлық алымы белгіленеді, ал одан кейін Пробел ді тағы да басқанда, барлық формула белгіленеді (2. 6-сурет) .
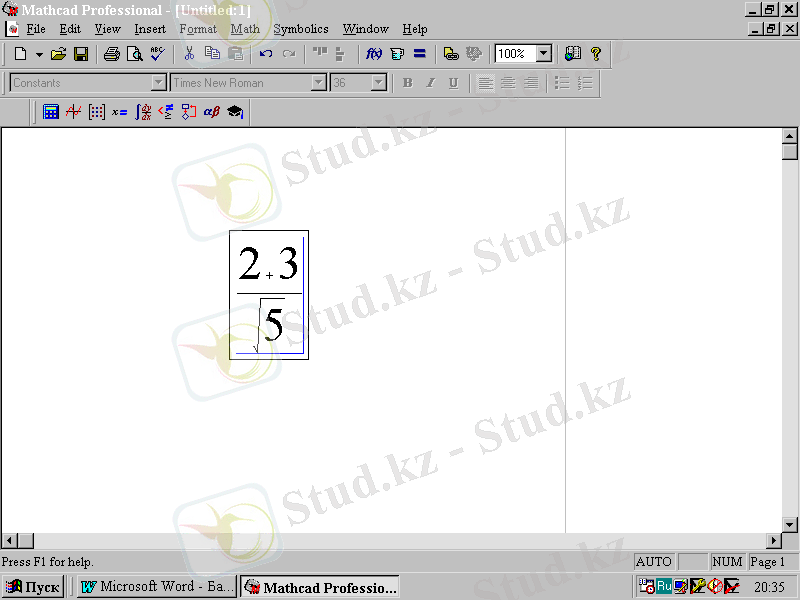 2. 6-сурет.
Теңдеуді толық белгілеу
2. 6-сурет.
Теңдеуді толық белгілеу
Шығару операторын = енгізгенде, Mathcad автоматты түрде есептеудің нәтижесін бейнелейді (2. 7-сурет) .
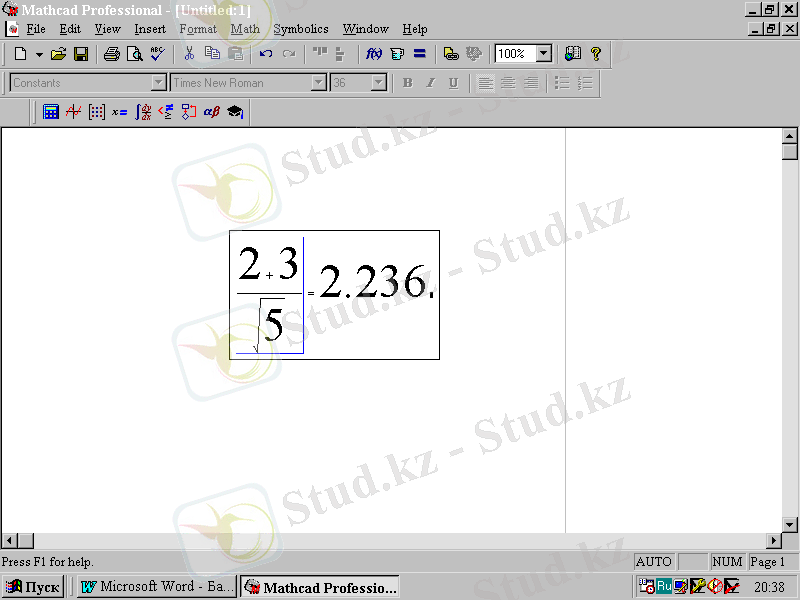 2. 7-сурет.
Шығару операторын енгізгеннен кейінгі формулалық блок
2. 7-сурет.
Шығару операторын енгізгеннен кейінгі формулалық блок
Mathcadты есептеудің түрлі эксперименттерін оңай қолдануға болады. Түбір астындағы 5-тің 1. 25 дәрежесіндегі нәтижені шығарамыз дейік. Ол үшін формуланы қайта жазудың қажеті жоқ. Ол үшін тышқан көрсеткішін 5 санынан кейін орналастырып, тышқанның сол жағын шертіңіз. Сонда енгізу курсоры 5 санын белгілейтінін байқаймыз (2. 8-сурет) .
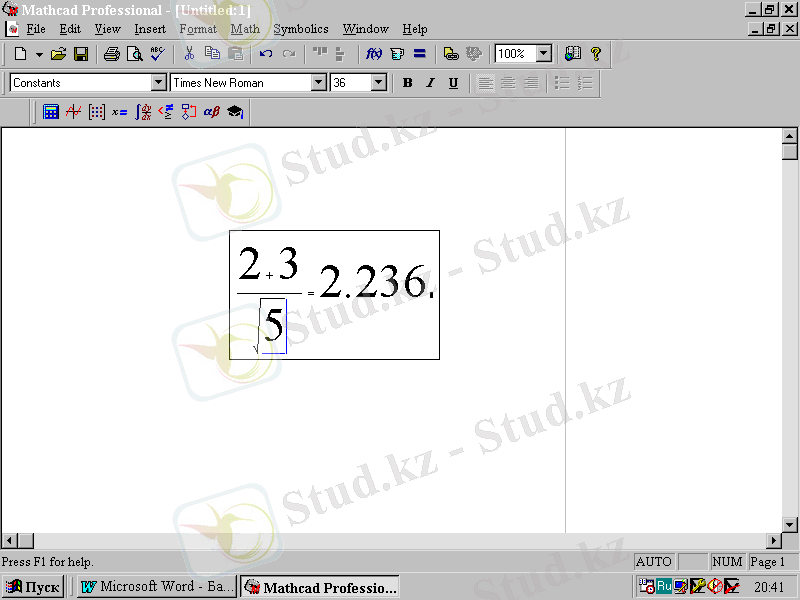 2. 8-сурет.
Формулалық блокта операнданың біреуін өзгерту
2. 8-сурет.
Формулалық блокта операнданың біреуін өзгерту
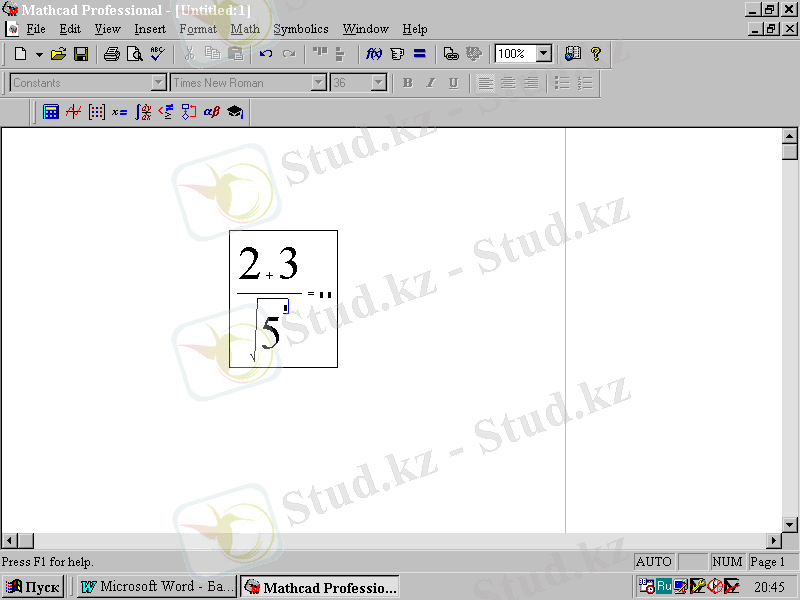 Енді санның дәрежесін шығару белгісін енгіземіз. Оны арифметикалық операциялар палитрасынан енгізуге немесе ^ белгісіндегі пернені басуға болады. Мұндайда формулалық блокта 5 санының дәрежесін жазу шығады (2. 9-сурет) .
Енді санның дәрежесін шығару белгісін енгіземіз. Оны арифметикалық операциялар палитрасынан енгізуге немесе ^ белгісіндегі пернені басуға болады. Мұндайда формулалық блокта 5 санының дәрежесін жазу шығады (2. 9-сурет) .
2. 9-сурет. Дәреже көрсеткіші операторын енгізгеннен кейінгі формулалық блок
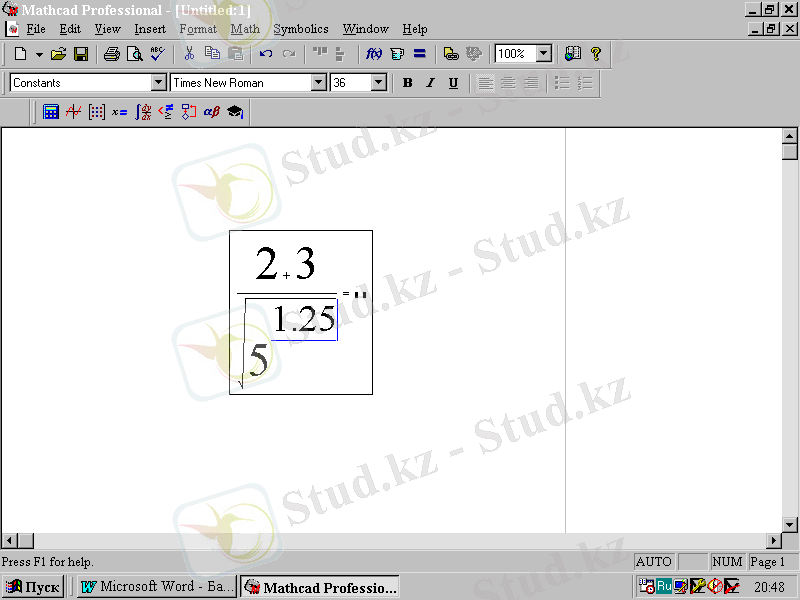 Енді 5 санының дәреже көрсеткішін шығарамыз.
Енді 5 санының дәреже көрсеткішін шығарамыз.
2. 10-сурет. 1. 25 дәреже көрсеткішін енгізгіннен кейінгі формулалық блок
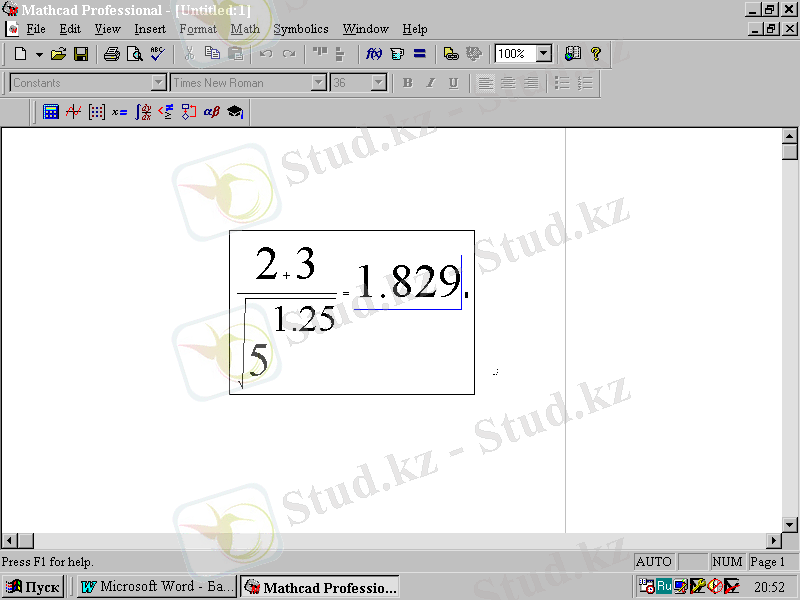 Әзірге енгізу курсоры 1. 25 санын белгілеп тұр (2. 10-сурет) . Есептеу үшін тышқан көрсеткішін формулалық блоктан алып кету жеткілікті. Сол кезде құрылған формула есептеледі (2. 11-сурет) .
Әзірге енгізу курсоры 1. 25 санын белгілеп тұр (2. 10-сурет) . Есептеу үшін тышқан көрсеткішін формулалық блоктан алып кету жеткілікті. Сол кезде құрылған формула есептеледі (2. 11-сурет) .
2. 11-сурет. Берілген формуланың есептелінуі
Бұл мысал математикалық формулалармен жұмыс мәнін көрсету үшін келтірілген.
1. 2. Меншіктеу және шығару операциялары
Кез-келген формуланы есептеу үшін одан кейін шығару операторын (= белгісі) орнату жеткілікті. Мұны бірнеше қарапайым мысалдар арқылы көрсетейік. Ондық сандарды енгізу үшін бүтін және бөлшек бөлімін ажырату ретінде үтір емес, нүкте пайдаланылады.
Енгізу Дисплей экранында
1. 234*2. 345= 1. 234 ⋅ 2. 345 = 2. 894
_1_
1/7= 7 =0. 148
cos(0. 5) = cos(0. 5) = 0. 878
e^2= eҚ = 7. 389
Математикада бірлік (общность) есептеулерді беру үшін берілген нақты типтегі бірнеше қорытылған белгі түріндегі айнымалылыр жиі қолданылады. Айнамалылар атаулары (идентификаторлар) бар, ал оларға мәндерді меншіктеу операциясы тән. Mathcad 2000-да алғашқы меншіктеу операторы ретінде = операторын қолдануға болады. Мұны қарапайым суреттеу түрінде көрсетейік.
Енгізу Дисплей экранында
a=2 a := 2
b=3 b := 3
a+b= a + b = 5
Енді жаңа мәндерді a және b айнымалыларына меншіктеуге әрекет жасағанымен, бұдан ештеңе шықпайды. Айнымалы атынан кейін = белгісін қоюға әрекет жасаймыз, айнымалының бұрынғы мәні шығады.
Енгізу Дисплей экранында
a= a = 2
b= b = 3
Жаңа мәнді айнымалыға меншіктеу үшін стандартты меншіктеу операторын := қолдануға тура келеді.
Енгізу Дисплей экранында
a:1 a := 1
b:1 b := 1
a+b= a + b = 2
Бұл мысалдардағы қарапайым есептеулерді орындауда Mathcad жұмысының кейбір ерекшеліктерін байқауға болады:
- кейбір есептелген операторлар (мысалы :=) бір символмен енеді;
- Mathcad арифметикалық операторларға дейін және одан кейін пробел қояды;
- көбейту операторы жұлдызша түрінде енеді, бірақ жолдың ортасында нүкте түрінде көрінеді;
- бөлу операторы қиғаш сызықша түрінде енеді, көлденең сызықшаға ауысады;
- санның дәрежесін табу операторы ^ белгісімен енеді, бірақ санның дәрежесі жоғарғы индекс ретінде көрінеді;
- келісім бойынша ондық сан бөлгіш нүктеден кейінгі үш белгісі бар түсінікті береді;
- Mathcad кең таралған константаларды, мысалые- натурал логарифм негізін түсінеді, сонымен қатарpі- ді де анықтайды;
- математикалық формулалар редакторлеудің типті қабылдаулары мен енгізу курсорын қолдану арқылы формулалық блок ішінде редакцияланады. 2. 12-суретте қарастырылған қарапайым есептеулер орындалған құжат көрсетілген.
2. 12-сурет Mathcad жүйесінде кейбір қосымша қабылданған жұмыстарды көрсетеді. Мысалы нүктеден кейінгі үш белгілі ондық сан сізге қолайсыз делік. Ол үшін санды форматтауды қолдану керек. Тышқан көрсеткішін санға алып барып, сол жақ батырманы екі рет басамыз. Сонда санды форматтау терезесі шығады. Number of demіcal places аумағында 3-тің орнына 15 санын қойып, ондық нүктеден кейінгі 15 белгілі нәтижені көресіз.
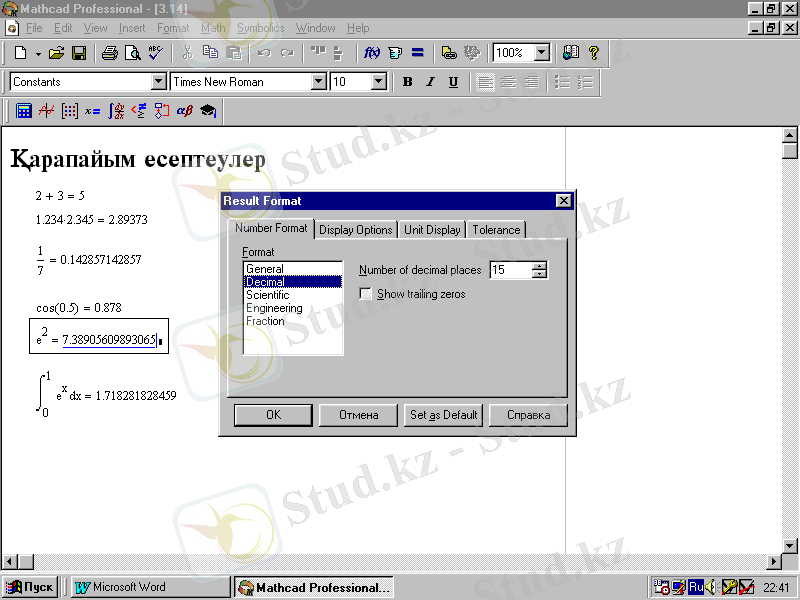
1. 12-сурет. Қарапайым есептеу көрсетілген Mathcad терезесі
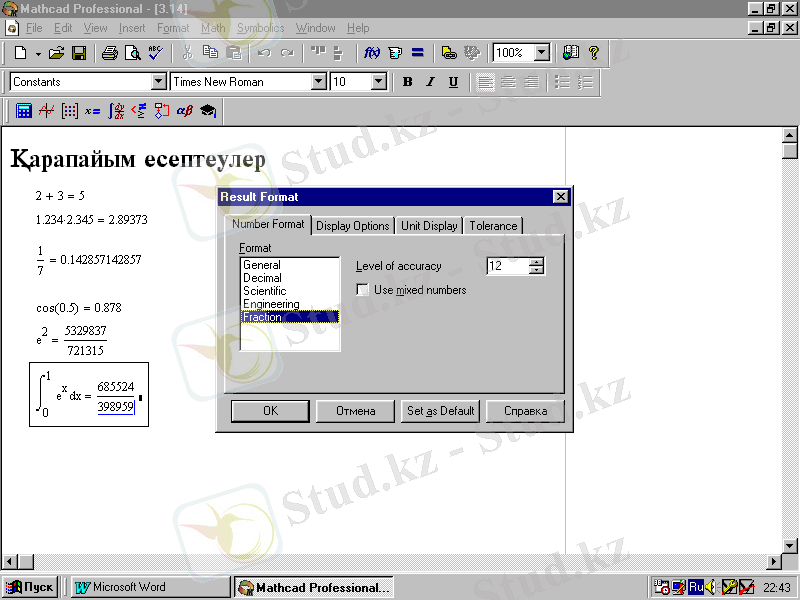 Mathcad 2001 де рационал сандар түріндегі қатемен берілген есептеудің нәтижесінің көрінісі жаңа мүмкіндігі енгізілген. Ол үшін санды форматтау терезесінде
Fractіon
форматын қосымша орнату шығады. Мұны жүзеге асыру 2. 13-суретте көрсетілген. Байқап отырғанымыздай берілген жағдайда Mathcad қарапайым ондық сан орнына бүтін санның қатынасы түріндегі оның мәнін береді (2. 13-сурет) .
Mathcad 2001 де рационал сандар түріндегі қатемен берілген есептеудің нәтижесінің көрінісі жаңа мүмкіндігі енгізілген. Ол үшін санды форматтау терезесінде
Fractіon
форматын қосымша орнату шығады. Мұны жүзеге асыру 2. 13-суретте көрсетілген. Байқап отырғанымыздай берілген жағдайда Mathcad қарапайым ондық сан орнына бүтін санның қатынасы түріндегі оның мәнін береді (2. 13-сурет) .
2. 13-сурет. Рационалды сандар форматында шығаруды демонстрациялау
2. 12, 2. 13-суреттердегі соңғы мысал анықталған интегралды түсіндірейік. Ол үшін Calсulus палитрасының суреттерінде көрсетілген интеграл шаблоны қолданылған. Mathcad үшін қарапайым мектеп оқушысының квадрат түбірін немесе инженердің анықталған интегралын шығару ма бәрібір. Көбейтінді немесе қосынды шаблондарын қолданып, мүшелінің көбейтіндісін немесе қосындысын есептеуге болады.
Массивтер, векторлар және матрицалармен жұмыс
Массивтер, векторлар және матрицалар - Маtһсаd жүйесінде қарастырылатын көптеген мәліметтерді өндеудің маңызды түрі. Бұл сабақта осы мақсатқа арналған тәсілдермен танысамыз.
Массивтер түрлері . Алдын-ала берілген айнымалының вектордан айырмашылығы - оны жеке мәндерде өзгертуге болмайтыңдығында, айталық екінші немесе бесінші - барлығы бірден қолданылады, оның жеке мәндеріне қатынауға болмайды. Бірнеше компонентті айнымалының әрбір мәндеріне қатынау қажетті болған жағдайда ол массив түрінде - бір өлшемді немесе екі өлшемді матрицалар түрінде берілуі қажет. Қатынау вектордың әрбір элементіне немесе массивке мәндер меншіктелуі мүмкін екендігін және әрбір элементке осы мәндерді есептеу арқылы жетуге болатынын білдіреді. Осылай, вектор элементі, мысалы V болса, V i индексті айнымалы болып табылады.
Массивтер сандық мәліметтермен қатар, символдық мәліметтерді де құрауы мүмкін.
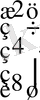 - сандық мәліметтермен берілген вектор бағанасы
- сандық мәліметтермен берілген вектор бағанасы
(а b + с d) - символды мәліметтермен берілген вектор қатары
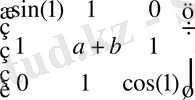 - түрлі типтегі элементті матрица
- түрлі типтегі элементті матрица
Осыған дейін белгілі болғандай, Маthсаd 2001-де векторлар мен матрицалар Маtһсаd-тың бұрынғы версияларындағыдай квадрат жақшада емес, ұзын дөңгелек жақшада беріледі.
Индексті айнымалыларды қолдану . Маthсаd -та массив те кез-келген айнымалы тәрізді атымен беріледі. Элементтің орны вектор үшін бір индекспен немесе матрица үшін екі индекспен беріледі. Индекстеудің төменгі шегі 0 немесе 1 (үнсіз келісім бойынша оның мәні О-ге тең) мәндерін қабылдайтын ORIGIN жүйелік айнымалысымен анықталады. Индекстер тек бүтін оң сандар (және ноль) болуы мүмкін. Индексті енгізу үшін [ - ашылған тік жақша белгісі қолданылады. Индексті айнымалыларды индексінде өзінің аты болатын скалярлы айнымалылармен жаңылыстыруға болмайды. Мысалы І 1 тогы, мұндағы төменгі индекс жай ғана "бірінші ток" дегенді білдіреді, кейбір электрлік схемалардағы 1 бұтақтағы ток. Осы тәрізді индекстер - айнымалы атын көрсететін индекс нүктенің көмегімен енгізіледі, енгізу курсорының көк бұрышы мұндайда индекстің енгізу облысын ғана емес, барлық атын қамтиды. Өкінішке орай, дисплей экранында индексті айнымалылар мен атын көрсететін индексті айнымалылар нашар ажыратылады: жалғыз айырмашылығы - индексі атын көрсететін скалярлы айнымалының индексі пробел арқылы ажыратылады, яғни ол индексті айнымалының индексіне қарағанда оң жақта орналасады. Ол былай көрінеді:
- х1- индексті скалярлы айнымалы;
- х2- индекстелген айнымалы.
Матрица элементтерінің аттары матрица атымен сәйкес келетін индекстелген айнымалы болып табылады. Мысалы, келесі матрицаны алуға болады:
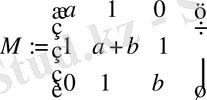
Бұл жағдайда екі индексті көрсетеді: біріншісі - қатар номері үшін, екіншісі - бағана номері үшін. Мысалы, егер көрсетілген М матрицасының орташа элементі ORIGIN =0 М 1, 1 дегенді, ал төменгі оң элементі М 2, 2 дегенді білдіреді.
Векторлар және матрицалар элементтерін енгізу . Векторлар мен матрицаларды олардың элементтерін енгізу жолы - индекстелген айнымалы арқылы беруге болады. Айнымалы атынан кейін қатар астына түсіріліп жазылатын индекстерді көрсету үшін ашылған квадрат жақша белгісі енгізіледі.
Матрица элементтері үшін катар астына түсіріп жазылатын индекстер оларды үтірмен бөлу арқылы енгізіледі.
Векторлар мен матрицаларды беру үшін не Маth (Вычисление - Есептеу) менюінің Маtrices командасын қолдануға, не Ctrl +V пернелер комбинациясын басуға, не матрица шаблоны бейнеленген батырманы шертуге болады. Осы іс-әрекеттердің кез-келген матрицаның өлшемін, яғни оның қатар т және бағана п санын көрсететін диалог терезесін шақырады. Векторлар үшін осы параметрлердің біреуі 1-ге тең болуы керек. m=1 болғанда, вектор кдтарын, ал п=1 болғанда, вектор бағанасын аламыз. Матрица тп элементтер саны бар екі өлшемді массив болып табылады.
Векторлар мен матрицаларды беру . Индекстелген айнымалылар үшін басқа қарапайым айнымалылар тәрізді меншіктеу және шығару ережелері де қолданылады. Массив шаблондарын қолмен толтырмай-ақ, өлшемі мен түрін беру арқылы меншіктеу операторының көмегімен массивті (вектор немесе матрицаны) құруға болады (5. 1-сурет) .
Сонымен қатар, бейнелеудің үлкен өлшемді массивті көрсетуді қамтамасыз ететін айналым сызықтары бар
электронды кесте түріндегі нұсқасы да бар.
ВЕКТОРЛАР МЕН МАТРИЦАЛАРДЫ БЕРУ
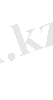
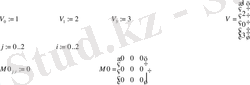

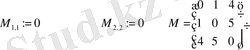 Арнайы матрица
Арнайы матрица
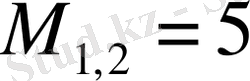
Векторлық және матрицалық операторлар
Маthсаd жүйесі векторлар мен матрицалар жұмысы үшін
операторлар мен функциялар қатарын қолданады. Алдымен,
төмендегідей мағыналарды ұстанатын операторларды
қарастырайық: V - вектор үшін, М - матрица үшін, Z- скаляр төбелер үшін.

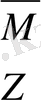

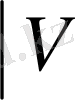
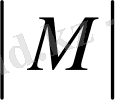
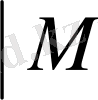

 $ V
$ V
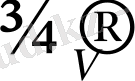
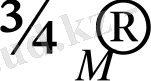
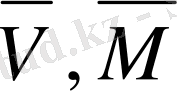
Кейбір операторларды енгізу үшін Сtrl пернесі қолданылатындығын айта кетейік, ал Маthсаd жүйесінің алдыңғы версияларында Аlt пернесі қолданылған болатын (соңғы версиясында Аlt пернесі меню қатарын активтеуге арналған) . Жоғарыда көрсетілген барлық операторларды (соңғысынан басқасын матрицалық операциялар палитрасынан шақыруға болады) .
Векторлау операторы
Келтірілген операциялардың көпшілігі матрицалық есептеудің математикалық аппаратынан белгілі. "Векторлау" түсінігімен қатар кейбір скаляр операцияларды іске асыру векторлау операторларымен белгіленген векторлар мен матрицалардың барлық элементтері түсініледі. Мүны параллель есептеулер мүмкіндігі деп те түсінуге болады.
Векторлау математикалық формулалардың мағынасын, тіпті Маthсаd -тың алдыңғы версияларыңда мүмкін болмайтын формулаларды өзгерте алады. Мысалы, егер V вектор болса, онда соs(V) формуласы мүмкін болмайды, себебі соs функциясының аргументі тек скаляр айнымалы болады. Алайда, соs(V) функциясы векторлау операторымен бастапқы V векторының элементіне сәйкес келетін әрбір элементінде косинусы бар векторды береді.
Маthсаd 8/2000/2001-ге кезекті жетістігі - функция аргументі ретінде матрицалар мен векторларды беруге болатындығы енгізілген. Осындай жолмен, V вектор болған жағдайда, соs(V) формуласы векторлау операторларын қолданбай-ақ мүмкін бола алады. Маthсаd 8/2000/2001 жүйесінде векторлау автоматты түрде орындалады. Осы жағдайда, біздің мысалымызда V векторының элементіне сәйкес келетін әрбір элементі косинусқа тең вектор беріледі.
Векторлау ұзын стрелка белгісі астындағы формуланың орны болып табылады. Мысалыға, егер А және В - векторлар болса, онда А • В осы векторлардың скаляр көбейтіндісін береді. Бірақ, бүл векторлау белгісі астындағы көбейтінді А және В векторларының j - шы элементі көбейтіндісі бар j-шы элементті жаңа векторды құрайды.
Сонымен, векторлау массивті скаляр операторлар және функцияларды қолдануға мүмкіндік береді. Бұл математикалық алгоритмдер жазбасын, әсіресе параллель есептеулерді қамтамасыз ету жазбасын қысқартады.
Векторлық және матрицалық функциялар
Маthсаd сызықтық алгебра және вектор мен матрицалар қосымшаларының баска да сферасындағы тапсырмаларды шешуді жеңілдететін тізілген векторлық және матрицалық функциялар
қатарын құрайды:
- length(V) - вектордың элементтер санын береді;
- last(V) -соңғы элементтің номерін береді;
- тах(V) -вектордың (немесе матрицаның) максимальдыэлементін береді;
- тіп(V) -вектордың (немесе матрицаның) минимальды элементінбереді;
- Rе(V) -вектордың нақты бөлігіндегі комплексті элементтівекторды береді;
- Іт(V) -вектордың жорамал бөлігіндегі комплексті элементтівекторды береді;
- (i, j, k) -үшінші рангың антисимметриялық тензордың бірліктолығы, мұндайдаі, j жәнеk(немесе егер ORIGIN≠0 болса, ORIGIN -нан ORIGIN -ге дейін) болуы керек; егер кез-келген екі аргумент тең болса, нәтиже 0-ге, егер үш аргумент жұп алмастыру (0, 1, 2) болып табылса 1 және егер үш аргумент тақ алмастыру (0, 1, 2) болып табылса, нәтиже -1 болады.
Матрицалык, функциялар . Матрицамен жұмыс істеу үшін сонымен бірге құрамдас функция қатары да бар:
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz