Сызық теңдеуі

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 21 бет
Таңдаулыға:

Жоспар

І. Кіріспе

«Сызық теңдеуі»

ІІ. Негізгі бөлім

а. Сызықтардың теңдеуін геометриялық қасиеттері бойынша құру.

б. Алгебралық сызықтар және оның реті.

Берілген теңдеуді қанағаттандыратын координаталардың екі - екіден алынған мәндерінің (нақты не жорымал) жиындысын сызық деп атаймыз. Осы жиын нақты болса, онда сызық көрнекі болып кескінделеді. Екі мысал келтірейік:

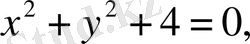
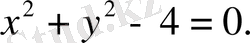
Бастапқы теңдеу х пен у- тің ешбір нақты мәндерінде қанағаттанбайды. Бұл нақты сықызты кескіндемейді. Екінші теңдеу х пен у- тің нақты мәндерін қанағаттандырады. Бұл жағдайда сызық көрнекі түрде кескінделеді.

Аналитикалық геометрияда кейбір сызықтарды нүктелердің геометриялық орындары деп қарастырамыз. Өйткені мұндай ұғымда сызықтың барлық нүктелерінің жалпы геометриялық қаситтері сақталады. Сызықтың декарттық системасындағы кез келген нүктесінің координаталарын х және у десек, осыған лайықты сызықтың барлық нүктелерін қанағаттандыратын х пен у- ті байланыстыратын теңдеуді құрамыз. Бұл теңдеуді сызықтың теңдеуі дейміз, ал осы теңдеуге енетін х пен у- ті сол сызықтың бойында жатқан нүктенің ағымдық координаталары дейміз. Сонымен, сызықтың бойындағы кез келген М(х, у) нүктесінің координаталарын қанағаттандырып, айнымалы х пен у шамаларын байланыстыратын теңдеуді берілген сызықтың теңдеуі дейміз.

Координаталар системасындағы сызықтың бойындағы кез - келген нүктенің х пен у координаталарын қанағаттандыратын теңдеуді былайша белгілейміз:

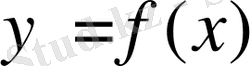
немесе

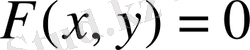
(1) теңдеуде у - тің мәні х арқылы шешілген. Екі айнымалы шаманың байланысы (1) теңдеуімен жазылса, онда мұндай функцияны анықталған функция дейміз. (2) теңдікте екі (х, у) айнымалы шаманың қайсысының функция екендігі белгісіз, яғни бір белгісіз екінші белгісіз арқылы шешілмеген. Мұндай функцияны анықталмаған функция дейміз. (1) және (2) теңдеулерінің жазықтықтағы геометриялык мәндері не түзу сызық, не қисық сызық болады, яғни олар не түзу, не қисық сызықты сипаттайды. Осыған мысалдар келтірейік.

1 - м ы с а л. у = 2х теңдеуі беріл-сін. Осы теңдеудің графигін салайық. Шешуі. Берілген теңдеудегі х- ке әр түрлі мән беріп, сол теңдеу арқылы у -тің мәндерін табамыз, яғни х = 0, у = 0; х=1, у = 2; х= - 1; у =-2 т. с. с. Енді осы нүктелерді декарттық координаталарға саламыз. Ал осы нүктелерден жүргізілген сызық түзу сызықтың графигі екендігін көреміз. у = 2х теңдеуі y= f (х) түрінде берілген. Ал бұл теңдеу F(х, у) = 0 түрінде берілсе, онда былай жазылады: у-2х = 0. Қарастырып отырған мысалымыздағы теңдеу қай түрде берілсе де координаталар системасында бас нүктеден өтетін түзу сызықтың теңдеуі болады.

2-м ы са л. 3 х + 2 y - 6 = 0 теңдеуі берілсін. Осы теңдеудің графигін салайық.

Шешуі. Мұндағы х пен y -тің мәндері мынадай болсын: х = 0 _, у = 3; х=1, y =1, 5; х = 2, y =0; х=3, y =-1, 5. Осыдан құрылған графикке қарағанда, бұл теңдеу бас нүктеден өтпейтін түзудің теңдеуі 3х + 2у - 6 = 0 теңдеуі - анықталмаған түрде [F (х, у) = 0] берілген теңдеу.

3-м ы с а л. у = х ² теңдеуі берілсін. Осы теңдеудің геометриялық. мәні қандай?

Шешуі. х пен y -тің мәндері мынадай болсын: х = 0, у = 0 ; x =1, y=І _; x = 2, у=4; х=-1, у =1; х =-2; y = 4. Осыдан шыққан график 21-сызбада көрсетілген.

Сонымен, теңдеуінің геометриялық мәні - координаталардың бас нүктесінен өтетін қисық сызық. Мұндай қисык сызық парабола деп аталады.

Осы келтірілген мысалдардан мынадай қорытынды шығады. Берілген теңдеуі бойынша декарттық не полярлық координаталар системасындағы түзу және қисық сызықтьщ графиктерін нүктелер арқылы салуға болады. Осы нүктелер неғұрлым жиі алынса, әрбір қисық сызықтың графигі соғұрлым дәл болады. Сонымен, жазықтықтағы геометриялық бейнелерді координаталар системасының методымен берілген теңдеуі бойынша сипаттаймыз. Қысқаша айтқанда х пен у немесе мен координаталарын байланыстыратын теңдеу берілсе, онда осы теңдеуге сәйкес жазықтықтағы сызықты құруға болады.

Математикада қарастырылатын теңдеулер алгебралық және трансценденттік болып екі топқа бөлінеді. Алгебралық теңдеу деп мынадай тендеуді айтамыз: m Мұнда әр түрлі белгімен алынған а, т, п сандары х пен у -ке тәуелді
емес. Барлық т және п - бүтін, оң таңбалы сандар. Алгебралық
емес теңдеулер трансценденттік деп аталады. Мысалы, тригономет-
риялық логарифмдік, көрсеткіштік теңдеулер
у=а ^х - трансценденттік теңдеулер болады. Аналитикалық геометрияда алгебралық теңдеулер қарастырылады да, осыған сәйкес және қисық сызықтар зерттелінеді.

Негізгі бөлім

Cызықтардың теңдеулерін геометриялық касиеттері бойынiа құру. Алдыңғы параграфта сызықтың графигін берілген алгебралық теңдеу бойынша салып көрсеттік. Енді сызықтың теңдеуін берілген геометриялық қасиеттері бойынша құруды үйренейік. Әрбір сызықты нүктелердің геометриялық орындары деп қарастырайық. Сонымен, сызықтың геометриялық қасиеті бойынша бір координаталар системасында кез келген нүктенің ағымдық координаталары арқылы алгебралық теңдеуді құрайық.

1. Бірінші координаталық бұрышты қақ бөлетін биссектрисанын теңдеуін табайық.

Бірінші координаталық бұрыштың биссектрисасы деп, сол бұрыштың қабырғаларынан бірдей қашықтықта болатын нүктелердің геометриялық орындарын айтамыз. Биссектрисаньщ кез келген нүктесін М, оның координаталарын х; у десек, онда жоғарғы айтылған биссектрисаның қасиеті у=х алгебралық теңдеуімен жазылады. Бұл теңдеу - бірінші координаталық бұрышты қақ бөлетін биссектрисаның теңдеуі.

2. Екінші координаталық бұрышты қақ бөлетін биссектрисанын, теңдеуін табайық.

Екінші координаталық бұрыштың биссектрисасы деп, сол бұ-рыштың қабырғаларынан бірдей қашықтықта жататын нүктелердің геометриялық орындарын айтамыз. Биссектрисаның бойындағы кез келген нүктені М\(х, у) десек (24-сызба), онда бұл нүктенің коор-динаталарын мынадай алгебралық теңдеу қанағаттандырады:

Осы екі теңдеудегі (у = х, у=-х) аргументтерге әр түрлі мән беріп,

соған сәйкес у -тің мәнде-рін тауып, нүктелерді қоссақ, биссектрисалардық графиктері шығады (24-сызба) .

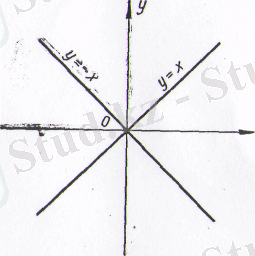
24-сызба

Сонымен, биссектрисалардың тік бұрышты координаталар системасындағы алгебралық теңдеулерін олардың қасиеттері бойынша жаздық.

3. Центрі берілген және радиусы белгілі шеңбердің теңдеуін табайық.

Анықтама. Центр деп аталатын берілген нүктеден бірдей қа-шықтықта жататын нүктелердіц геометриялық орындарын шецбер дейміз.

Шеңбердің центрінің координаталары а, b және радиусы R болсын. Шеңбердің центрін С нүктесімен белгілейік те, оның бойында жатқан кез келген М(х, у) нүктесін алайық.

М және С нүктелерінен абсцисса осіне перпендикуляр түсіріп (25-сызба), С нүктесінен абсцисса осіне параллель сызық жүргізсек, СМF үшбұрышы шығады. 25-сызбадан:

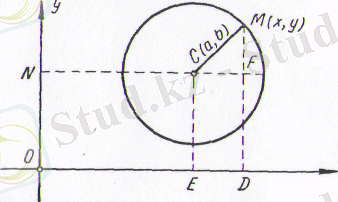
ОЕ = NС = = а, ON=EC=b, CF=OD-OE=NF-NC= х- а, FМ=DМ-DF- ЕС= у-b.

СМF тік бұрышты үшбұрышынан: 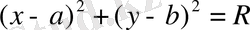, мұндағы СМ =R.

Егер СМ>R, СМ<R болса М(х, у) нүктесі шеңбердің бойында жатпайды. Бұл теңдеуді екі нүктенің арасындағы қашықтықтың

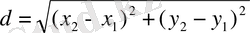
формуласы бойынша да дәлелдеуге болады. Ал 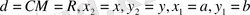мәндерін екі нүктенің арасындағы қашықтықтың формуласына қойсақ, мынадай теңдеу шығады:

(х-а) ² +(у-b) ² = R ² , (3)

мұндағы R - радиус, х, у - шеңбердің бойындағы кез келген нүктеніц агымдық координаталары. Бұл теңдеу шеңбердің нормальдық теңдеуі деп аталады. Енді осы теңдеуді түрлендіріп, шеңбердің жалпы теңдеуін табайық:

х ² - 2ах + а ² + у ² - 2bу + b ² -R ² = 0,

ал

- 2а = А, - 2b=В, а ² + b ² - R ² = С деп белгілесек,

х ² + у ² +Ах + Ву + С = 0 (4)

болады.

Егер шеңбердің центрі координаталардың бас нүктесінде жатса, онда

а = 0, 6 = 0 болады, ал (3) теңдеуден мынадай теңдеу шығады:

х ² +у ² = R ² . (5)

4. 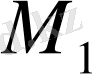( 1 , 1), М ₂ (- 1, 2) нүктелерінен бірдей қашықтықта жатқан нүктелердің геометриялық орындарын сипаттайтын теңдеуді табайық.

Белгісіз геометриялық орындардың бойындағы нүктені М(х, у) деп белгілесек, есептің шарты бойынша мынадай теңдікті жазамыз: М~М ₂ М. Екі нүктенің арасындағы қашықтықтың формуласын колдансақ: 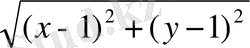= 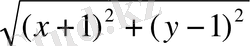немесе х ² -2х+1+у ² -2у+1=х ² + 2х+1+у ² -4у+4, мұнан 4 x -2 y +3=0 теңдеуі шығады. Бұл теңдеу берілген және М ₂ нүктелерінен бірдей қашықтықта жатқан нүктелердің геометриялық орындарын сипаттайды. 4х- 2у +3=0

5. (1, 0) және М ₂ (4, 0) нүктелері берілген. Бір М нүктесі М ₂ нүктесінен гөрі нүктесіне ылғи екі есе жақын қозғалып отырады дейік. Осы М нүктесінің траекториясы қандай?

Шешуі. Белгісіз М нүктесінің ағымдық координаталарын х және у десек, онда M(x, y) болады. Есептің шартында көрсетілген қозғалмалы М(х, у) нүктесінің қасиеті бойынша: 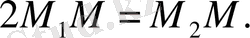Екі нүктенің арасындағы кашықтықтың формуласын қолдансақ:

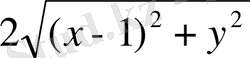
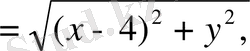
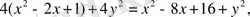
3 х ² + 3 у ² =12, х ² +у ² = 4 теңдеуі шығады. Бұл - радиусы екіге тең, центрі координаталардың бас нүктесінде жататын шеңбердің теңдеуі.

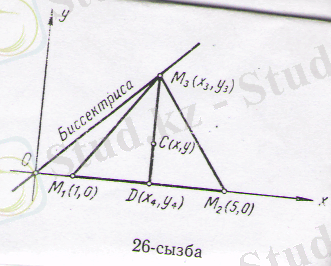
6. Үшбұрыштың екі ( 1 , 0), М ₂ (5, 0) төбесі берілген, оның үшінші төбесі координаталық биссектрисаның бойында жатыр. Осы үшбұрыштың ауырлық центрінің геометриялық орындарын табайық.

Шешуі. Есептің шартына сәйкес сызба салайық (26-сызба) .

Биссектрисаның бойындағы нүктені М ₃ (х ₃ , у ₃ ) деп белгілейік. Осы нүктеден М ₃ D медианасын жүргізіп, D нүктесінің координаталарын деп белгілейік. Үшбүрыштың центрі С медианасын мынадай бөлікке бөледі: немесе . Кесіндіні берілген қатынаста бөлу формуласы бойынша:

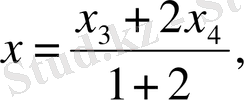
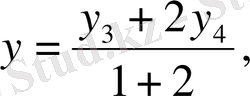
Енді М ₂ кесіндісінен мынау шығады:

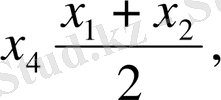
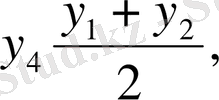
және у ₄ -тің мәндерін жоғарғы теңдіктерге қойып, мынаны табамыз:

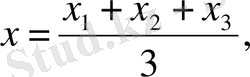
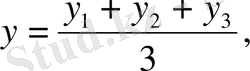(6)

Бұл - үшбұрыштың центрінің координаталарының формуласы. Үш-бұрыштың центрін оның төбелерінің координаталары аркылы табуға болады. (6) формула бойынша:

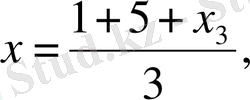
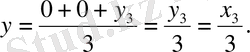
М ₃ нүктесі биссектрисаның бойында жатқандыктан . Соңғы теңдеуден Осы х ₃ -тің мәнін алдыңғы теңдеуге қойып, іздеген геометриялық орындардың теңдеуін табамыз:

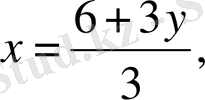3x=6+3y, x-y-2=0

х, у - терді өзінің (*) өрнегімен алмастырған соң 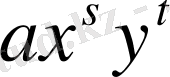мүшенің орнына мынадай өрнек шығарып аламыз:

(* *)

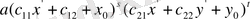және түріндегі өрнектердің қосындысы болады. Демек, 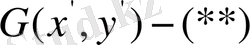және айнымалыларға қатысты көпмүшелік болып табылады.

Егер (**) өрнегіндегі жақшаларды ашып, ұқсас мүшелерін келтірсек, онда 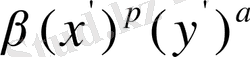түріндегі мүшелердің қосындысын шығарып аламыз, мұнда осындай әрбір мүшенің дәрежесі . Демек,

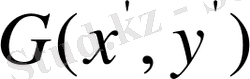дәр. 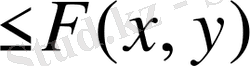дәр. (3)

Енді ескі коордиталар системасы, ал жаңа координалар системасы деп есептейік, дәлелденген бойынша

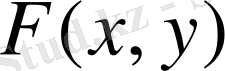дәр. дәр.

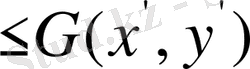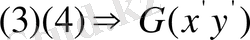дәр. 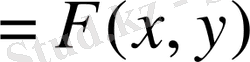дәр. (4)

2. Алгебралық емес сызықтардың шексіз жиыны бар болады. Айталық, тік координаталар системасында теңдеулермен анықталатын сызықтар емес сызықтарға мысал бола алады. Бұл сызықтардың қандай да біреуі (2) теңдеумен, мұнда координаталар системасы болмайды. Шынында, егер ондай репер. бар деп ұйғарсақ, онда реперінен реперіне көшкенде, біздің сызық реперінде (1) теңдеу түрінде анықталар еді, мұндағы - көпмүшелік, бұл әрине шартқа қайшы келеді.

3. Сызықтарды алгебралық, және алгебралық емес сызықтар деп екі классқа бөлу аффиндік координаталар системасының қолданылуына негізделгендігін ескертейік.

Алгебралық сызық және орның реті.

1. Егер қандай болсын бір аффиндік координаталар системасында жазықтықтағы сызықтың теңдеуін

(1)

түрінде беруге болса, онда ол сызықты алгебралық сызық деп атайды, мұнда айнымалысынан алынған көпмүшелік, яғни саны шектеулі 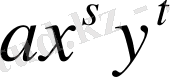түріндегі мүшелердің қосындысы. - теріс емес бүтін сандар) . 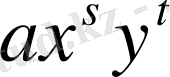мүшесінің дәрежесі деп санын айтады. 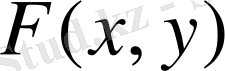көпмүшеліктің дәрежесі деп оның мүшелерінің ең үлкен дәрежесін айтады. ; ол 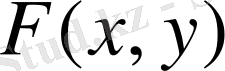дәрежесі деп белгіленеді. 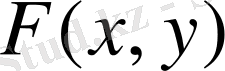көпмүшеліктің дәрежесі (1) теңдеумен анықталатын сызықтың реті деп аталады.

Мысал. Тік бұрышты координаталар системасында шеңбердің

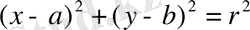
Теңдеумен анықталатынын білеміз. Демек, шеңбер - екінші ретті сызық.

Теорема: Сызықтың реті аффиндік координаталар системасын сайлап алуға тәуелді емес.

Жазықтықта аффиндік координаталар системасы беріліп және осы системада вектор сызығы (1) теңдеумен анықталатын болсын, мұнда F (x, y) - n дәрежелі көпмүше:

F (x, y) дәр. = n

Екінші бір афффиндік координаталр системасын, алайық. Кез келген М нүктесінің ескі координаталары x, y оның жаңа координаталары 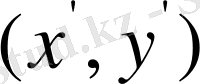арқылы мына

(*)

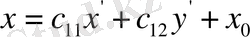
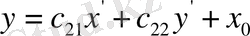формулалар бойынша өрнектеледі. Вектор сызығының реперге қатысты теңдеуін шығарып алу үшін (1) теңдеудегі x, y мәндерін (*) формулалар бойынша алмастырамыз. Сонда мынадай бір теңдеу шығады.

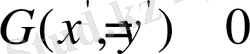(2)

Бірақ та F (x, y) - 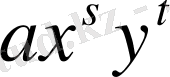түріндегі мүшелердің қосындысы.

Жоспар

І. Кіріспе

Минорлар мен алгебралық толықтауыштар.

ІІ. Негізгі бөлім.

а. Матрица көбейтінділерінің анықтауышы.

б. Лаплас теоремасы.

Кіріспе.

Минорлар мен алгебралық толықтауыштар.

Анықтама. n- ретті анықтауыштың 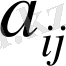элементінің 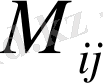миноры деп, осы анықтауыштың і жатық, тік жолдарынсыз алынған (n - 1) - ретті анықтауышты айтамыз, яғни:

Анықтауыштың 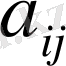элементінің 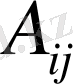алгебралық толықтауышы деп, (-1) 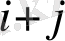таңбасымен алынған осы 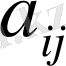элементтің минорын айтамыз, яғни:

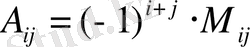
1. 3 - теорема. Егер анықтауыштың - тік (жатық) жолының 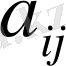элеменінен өзге барлық элементтері нөлге тең болса: 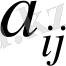=0, . . . , 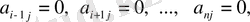онда анықтауыштың мәні 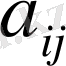элементімен оның 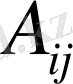алгебралық толықтауышының көбейтіндісіне тең:

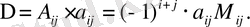
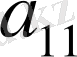Дәлелдеуі. Ең алдымен анықтауыштың элементімен басқа бірінші тік жолының барлық элементі нөлге тең жағдайды қарастырайық:

Анықтауыштың есептеу формуласының әр қосылғышында бірінші тік жолының бір-бір элементтері бар екенін еске онда анықтауыштың есептеу формуласындағы 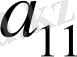элементі бар қосылғыштардан басқа қосылғыштар нөлге тең. Ендеше,

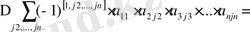
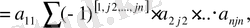
мұндағы индекстері 2, 3, . . . , п мәндерін қабылдайды. Егер де бірінші орында тұрған 1 бірде инверсия құрмайтынын ескерсск, яғни [1, ] = [ ] онда

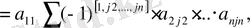
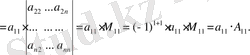
Енді тік жолының элементінен өзге барлық элементтері нөлге тең анықтауышын қарастырайық:

Осы анықтауыштың і жатық жолын і -1 жатық жолымен орын алмастырсақ, одан соң оны і-2 жатық жолымен, және тағы сол сияқты, ең соңында оны бірінші жатық жолымен орын алмастырсақ, анықтауыштың 2-қасиетін ескерсек, онда

Соңғы анықтауыштың - тік жолын -1 тік жолымен, одан кейін оны - 2 жолымен т. с. с. ең соңында бірінші тік жолмен орын алмастырсақ және анықтауыштың 2-қасиетін ескерсек, онда