Rn кеңістігі: метрикалар, нормалар, скаляр көбейтінді және сызықты функционалдар мен операторлар
Мазмұны.
Кіріспе . . . 2
I тарау. n-өлшемді векторлық кеңістік . . . 3
§1. R
n
анықтамасы . . . 3
§2. R
n
кеңістігіндегі метрика . . . 5
§3. R
n
кеңістігіндегі норма . . . 9
§4. R
n
кеңістігіндегі скаляр көбейтінді . . . 11
II тарау. R
n
кеңістігіндегі сызықты функционал
және сызықты оператор . . . 14
§5. R
n
кеңістігіндегі сызықты функционал . . . 14
§6. R
n
кеңістігіндегі сызықты оператор . . . 16
§7. Түйіндес және өзіне-өзі түйіндес оператор . . 20
Қорытынды . . . 23
Пайдаланылған әдебиеттер . . . 24
Кіріспе.
Бұл курстық жұмыста n-өлшемді векторлық кеңістік қарастырылады. Ол 2 тараудан және 7 параграфтан тұрады:
§1-де R
n
векторлық кеңістігінің анықтамасы беріледі.
§2-де Метрика ұғымы енгізіліп, R
n
кеңістігіндегі метриканың 4 түрі көрсетіледі.
§3-те R
n
кеңістігіндегі норма ұғымы енгізіледі. R
n
кеңістігіндегі норманың 3 түрі қарастырылады. Сол 3 норманың эквиваленттілігі айтылады.
§4-те скаляр көбейтіндінің анықтамасы және ортогональ векторлардың анықтамасы айтылады.
§5-те функционал жайлы анықтама беріліп, сол функционалдың сызықты болатыны көрсетіледі. Сызықты функционалдың нормасына да тоқталып, мысалдар келтіріледі.
§6-да R
n
кеңістігіндегі сызықты оператор жайлы айтылады. Ол 2 тақырыптан тұрады:
Сызықты оператордың анықтамасы айтылады.
Rn-ді Rmбейнелейтін сызықты оператордың жалпы түрі қарастырылады.
Сызықты оператордың нормасына да тоқталып кетіледі.
§7-детүйіндес және өзіне-өзі түйіндес операторлар қарастырылады. Мұнда операторды матрица түрінде беріп, сол матрицаға түйіндес матрица табылады. А=A
*
болса, онда А операторы өзіне-өзі түйіндес болатыны айтылады
I-тарау.
n-өлшемді векторлық кеңістік .
§1. R
n
анықтамасы .
Вектор ұғымы математиканың негізгі ұғымдарының бірі болып саналады.
Анықтама: Вектор деп жинақталатын (
\[{\tilde{d}}_{1},{\tilde{d}}_{2},\cdot{\cdot{\tilde{d}}_{n}}\]
) және белгілі бір ретпен орналасқан
\[{\tilde{d}}_{1},{\tilde{d}}_{2},\cdot{\cdot{\tilde{d}}_{n}}\]
(n -
\[\textstyle\bigvee\]
натурал сан) натурал сандар тізбегін айтамыз. Векторды бір әріппен белгілейміз де, ол төмендегідей жазылады
\[{\mathcal Q}\,\]
= (
\[{\tilde{d}}_{1},{\tilde{d}}_{2},\cdot{\cdot{\tilde{d}}_{n}}\]
)
\[{\tilde{d}}_{1},{\tilde{d}}_{2},\cdot{\cdot{\tilde{d}}_{n}}\]
сандарын а векторының координаттары деп атаймыз.
\[{\mathcal Q}\,\]
= (
\[{\tilde{d}}_{1},{\tilde{d}}_{2},\cdot{\cdot{\tilde{d}}_{n}}\]
) және
\[b=(b_{1},b_{2},...,b_{n})\]
векторларын тең деп атаймыз, сонда тек сонда ғана
\[a_{i}=b_{i}\]
болғанда
\[i={\overline{{1,n}}}\]
Барлық координаттары нөлден құралатын векторды нөлдік вектор деп атаймыз да, ол былай белгіленеді Ө.
\[{\mathcal Q}\,\]
және
\[\mathit{\mathcal{I}}\]
векторларының қосындысы деп
\[{\mathcal Q}\,\]
\[-\downarrow\leq{\sqrt{{\cal D}}}\]
векторына айтамыз. Ол төмендегідей формуламен анықталады:
\[{\mathcal Q}\,\]
\[+b=(a_{1}+b_{1},a_{2}+b_{2},...,a_{n}+b_{n})\]
Сол сияқты а векторының
\[\mathcal{A}\]
-нақты санына көбейтіндісі былай анықталады:
(
\[l\;\dot{a}=l\;\dot{a}_{1},l\;\dot{a}_{2},...,\lambda\;\dot{a}_{n}\]
)
Жоғарыдағы анықтамалардан векторлар үшін келесі алгебра заңдары орындалады.
1)
\[\hat{d}+J=D+Q\]
(комутативтік қосынды)
2)
\[(a+b)+c=a+(b+c)\]
(ассоциативтік қосынды)
3)
\[l~(\dot{a}+b)=l~a+\lambda~b\]
(дистрибутивтік көбейтінді
4)
\[(l\leftrightarrow m)\dot{a}=l\ a+\mu a\]
мен қосынды)
5)
\[l~(m\Delta)=(\lambda\mu~)a\]
(ассоциативтік көбейтінді )
6)
\[0^{\times}\dot{a}=\]
ө
7)
Екі вектордың айырымы келесідей анықталады.
\[a-\ b=a+(-1)b\]
Яғни
\[a-\ b=(a_{1}-\ b_{1,},a_{2}-\ b_{2,},...,a-b_{n})\]
Онда осы айырымнан келесі кері қосынды шығады
\[(a-b)+b=a\]
Нөлдік вектордың келесі қасиетке ие екендігін байқаймыз.
\[\tilde{a}+\hat{\imath}\,=a\]
\[\forall a\]
үшін.
Барлық векторлар жиынын n-өлшемді векторлық кеңістік деп атаймыз.
Бұл кеңістікті біз келесіде R
n
деп жазамыз. Барлық n-өлшемді векторлық кеңістіктерді өлшемді деп атаймыз.
R
n
кеңістігінің ортогональ координатасы деп бір координатасы 1-ге тең, ал қалған координаттары нөльге тең векторды айтамыз.
е
1
=(1, 0, …, 0)
е
2
=(0, 1, …, 0)
e
n
=(0, 0, …, n)
\[{}^{\mathrm{t}}\,{\dot{\alpha}}=(a_{1},a_{2},...,a_{n})\in\]
Equation. 3 R
n
векторын мына түрде жаза аламыз.
\[a=a_{1}{}^{\star}e_{1}+a_{2}{}^{\star}e_{2}+\ldots+a_{n}{}^{\star}e_{n}\]
(1)
Олай болса
\[Q_{i}\]
координаттары е
i
бірлік векторында
\[\mathbf{\hat{d}}\]
векторының проекциясының ролін атқарады.
§2. R
n
кеңістігіндегі метрика.
Анықтама 1: Е
\[\mathcal{Y}\]
элементтерден тұратын жиын болсын.
Егер Е жиынның
\[\forall x.y\]
нүктелеріне кейбір
\[\rho\left(x,y\right)\]
теріс емес санды сәйкестендіретін
\[\mathcal{P}\]
:
\[x*x\rightarrow R^{\prime}\]
функция анықталған болып
1)
\[\rho\left(x,y\right)\,\ge0,\]
\[\rho\left(x,y\right)=\ 00\quad x=y\]
2)
\[r\left(x,y\right)=\rho\left(y,x\right),\]
\[{}^{n}\,x,y\in E\]
3)
\[r\,(x,y)\propto\,r\,(x,z)+\rho\,(z,y),\]
\[{}^{\nu}\,\times_{,}\,y_{,}\,z\in E\]
1) -3) шарттарды қанағаттандырса метрика деп атайды.
Анықтама 2: Егер Е жиында
\[\mathcal{P}\]
метрика анықталған болса, онда
\[({\mathcal{X}},\rho\,)\]
-ны метрикалық кеңістік деп атаймыз.
Лемма 1: Егер
\[{\frac{1}{p}}+{\frac{1}{q}}=1\]
болса, онда
\[u^{\ast}v\;\pounds\;{\overset{d^{p}}{p}}+{\frac{v^{q}}{q}}\]
теңсіздігі орындалады.
Дәледеуі:
\[a\;>0\;\mathrm{P}\;\;\;y=x^{a},a\;>1\]
\[y=x^{a},a=1\]
\[\alpha\ <1\]
\[S_{1}=\stackrel{u}{\sim}\int^{a}d x;\]
\[S_{2}=\stackrel{u}{\textstyle\bigcup}^{\frac{1}{\alpha}}d y;\]
\[S_{1}=\frac{x^{a+1}}{a+1}\mid_{0}^{u}=\frac{u^{a+1}}{a+1}\]
\[S_{2}=\frac{y^{a+1}}{4}\mid_{0}^{\nu}=\frac{\nu^{a+1}}{a}\]
\[P=a\ +1\,\mathrm{P}\ \ {\frac{1}{P}}={\frac{1}{a+1}}\]
\[{\frac{1}{q}}=1-{\frac{1}{P}}=1-{\frac{1}{a+1}}{\frac{a}{a+1}}\not\,\textbf{p}q={\frac{a+1}{a}}\]
Лемма 2:
\[{}^{n}\,a,b\in R\]
сандар
\[{\mathfrak{p}}\gg1\]
саны үшін
Дәлелдеуі :
1)
2)
Теорема 1:
\[f\hat{{\imath}}\;\;L_{p},q\hat{{\imath}}\;\;L_{p},\frac{1}{{\cal P}}+\frac{1}{q}=1\]
\[p,q>1\,{\mathrm{P}}\ \ {\mathfrak{Q}}f(x)^{p}d x=L_{p},{\mathfrak{Q}}{\mathrm{e}}(x)^{q}d x=L_{q}\ {\Bigr|}{\Bigr[}f^{*}g{\Bigr]}d x<\infty\]
Гёльдер теңсіздігі . Егер
\[p=q=2\]
болса, онда Коши-Буняковский теңсіздігі келіп шығады.
Теорема 2: Егер
\[q,p>1,{\frac{1}{p}}+{\frac{1}{q}}=1\]
болса
\[\mathop{\stackrel{\mathrm{V}}{\Delta}}^{\textrm{P}}\Big|u_{k}\Big|^{P}<\frac{\Omega}{4}\!\!\Big|\mathcal{V}|^{q}<\infty\]
болса, онда
Енді 1-ші теореманы дәлелдейік.
\[u={\frac{\left|f{\bigl(}x\right)}{\left|\left|f\right|^{p}d x\right|}}\]
\[u^{\ast}v\;\pounds\;{\overset{u^{p}}{p}}+{\frac{v^{q}}{q}}\]
Теорема 3: Егер
\[p>1,f\bar{1}\ \ L_{p},g\in L_{p}\]
болса, онда
\[\left|f+g\right|\in L_{p}\]
және
\[\underline{{{\epsilon}}}_{{\S}}\Im f+g{\vert}^{p}d x_{{\Vert}}^{{\frac{1}{\Omega}}}\pounds\left\{\Im^{p}d x\right\}+\left[\vert{\xi}\vert^{p}d x\right]\]
Минковский теңсіздігі .
Дәлелдеуі:
2-лемма бойынша
\[\left(p-1\right)q=p\]
болғандықтан
Негізгі метрикалық кеңістіктер.
\[\begin{array}{r}{{R^{*}=\left\{x;x=(x_{1},x_{2},\ldots,x_{n})\right\}}}\\ {{1)p_{i}(x,y)={\sqrt{\frac{\hat{\alpha}}{k_{n}}}}(x_{k}\cdot y_{k})}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\\ {{\mathrm{~}}}\end{array}\]
соңғы 4-ті дәлелдейік.
Анықтама : Е жиында
\[p_{1}p_{2}\]
метрикалар анықталған болып
\[{}^{\circ}\,x,y\in E\]
элементтері үшін
\[\mathrm{Sc}_{1},c_{2}>0\]
табылып,
\[c_{1}p_{1}(x,y)\mathbb{E}\ p_{2}(x,y)\leq c_{2}p_{1}(x,y)\]
теңсіздіктері орындалса, онда
\[p_{1}\approx p_{2}\]
эквивалентті R
n
кеңістігінде 1) -4) метрикалар бір-біріне эквивалент.
§3. R
n
кеңістігіндегі норма.
3 өлшемді кеңістіктегі вектордың ұзындығына ұқсас R
n
кеңістігінде де
\[\mathbf{\hat{d}}\]
векторының ұзындығы мен нормасы деген түсінікті енгізуге болады.
Анықтама 1: R
n
кеңістігінде вектордың нормасы деп мына санды айтамыз.
\[\left\|a\right\|={\sqrt{a_{1}^{2}+a_{2}^{2}+\ldots+a_{n}^{2}}}={\sqrt{\sum_{k=1}^{n}a_{k}^{2}}}\]
Норманың басты қасиеттері:
\[\iota^{0}\lVert a\rVert\geq0\]
\[\forall a\]
үшін және
\[\lVert a\rVert=0\ \hat{U}\ \ a=\theta\,;\]
\[\begin{array}{l}{{2^{0}\Vert{\cal L}\,a\Vert=\Vert{\big\Vert}a\Vert,\nonumber}}\\ {{\downarrow}}\\ {{3^{0}\Vert a+D\Vert\,\tilde{\bf z}\Vert a\Vert+\Vert b\Vert}}\end{array}\]
1
0
, 2
0
қасиеттері көрініп тұр. 3
0
-қасиет Минковский теңсіздігінен келіп шығады.
\[p=q=2\]
болған жағдайда
R
n
кеңістігінде норманы басқа да формулалармен көрсетуге болады.
Мысалы
\[\prod_{1\leq i\leq n}\left(|a_{1}|,|a_{2}|,\ldots,|a_{n}|\right)\]
Бұл норманың да 1) -3) қасиеттерін қанағаттандыратынын көрсетейік.
1)
\[\left\Vert a\right\Vert\ \geq0\]
екені көрініп тұр.
Егер
\[\left\Vert a\right\Vert_{1}=0\]
болса, онда
\[\prod_{1\leq i\leq n}\left(|a_{1}|,|a_{2}|,...,|a_{n}|\right)\]
=0 яғни
\[\left|Q_{1}\right|,\left|Q_{2}\right|,\ldots,\left|Q_{n}\right|\]
сандарының ең үлкені нөлге тең. Онда барлық
\[i={\overline{{1,n}}}\]
үшін
\[\left|a_{i}\right|=0\]
яғни
\[{\mathcal Q}\,\]
векторы
\[a_{1}=0,a_{2}=0,...,a_{n}=0\]
координаталардан тұрады.
\[\hat{\mathrm{U}}\ \ a=(0,0,...,0)=\theta\]
нөлдік вектор.
2)
3)
\[\left\|a+b\right\|_{1}=\prod_{1\leq i\leq n}\left(a_{1}+b_{1}|,|a_{2}+b_{2}|,...,|a_{n}+b_{n}|\right)\]
\[i={\overline{{1,n}}}\]
үшін көрініп тұр .
\[\left|a_{i}+b_{i}\right|\mathcal{\leq}\left|a_{i}\right|+\left|b_{i}\right|\]
онда
\[\prod_{1\leq i\geq n}\!\!\!\!\mathrm{\tilde{|}}{a\!\!\!/}_{i}\!\!\mid\!\!a_{i}+b_{i}\!\!\mid\leq\prod_{1\leq i\leq n}\!\!\!\!\!\sf L\!|a_{i}|+\prod_{1\leq i\leq n}\!\!\!\!\!\subset\!\!\!\!\!\!\!\!\int_{i}\!\!\!\!\!\subset\!\!\!\!\!\!\!\!\ S\!\!\!/(b_{i})\]
яғни
\[\displaystyle{\prod_{n k l,K}(a_{1}+b_{1})|a_{2}+b_{2}|....|a_{n}+b_{n}|})\displaystyle{\pi}\,\mathop{\prod_{n:K,K}}\left(\langle a_{1}\rangle|a_{2}|...._{n}|a_{n}|\rangle+\prod_{n k\times{\bf X}}\left(\langle b_{1}|,|b_{2}|,..._{n}|b_{n}|\right)\right)=\left|a_{1}|+\left|b_{1}\right|,...\right|,\]
Демек
\[\left\|a+b\right\|\mathbb{Z}\left\|a\right\|+\left\|b\right\|\]
Келесі мысалда R
n
кеңістігіндегі
\[{\mathcal Q}\,\]
элементінің нормасы функция болуы мүмкін.
\[\left\|a\right\|_{2}=\sum_{i=1}^{n}a_{i}\]
Бұл функция үшін де 1) -3) қасиеттерінің орындалатынын көрсетейік.
1)
\[\sum_{i=1}^{n}a_{i}|=0~{\mathrm{P}}~~a_{i}=0\]
\[i={\overline{{1,n}}}\]
. Яғни
\[a=(0,0,...,0)=\theta\]
;
2)
3)
\[\left\|a+b\right\|_{2}=\underbrace{\partial}_{i=1}^{a}\left|a_{i}+b_{i}\right|\textbf{t}\left.\leq\underbrace{\partial}_{i=1}^{a}\left(a_{i}\right|+\left|b_{i}\right|\right)=\underbrace{\partial}_{i=1}^{a}\left|a_{i}\right|+\sum_{i=1}^{a}\left|b_{i}\right|=\left\|a\right\|_{2}+\left\|b\right\|_{2};\]
Сол себептен
Анықтама 2
:
Кейбір Е сызықты кеңістікте нормалар
\[\left\|{\vec{x}}\right\|_{1}\left\|{\vec{u}}\right\|\]
болып анықталсын.
Егер
\[{}^{n}\,x\ \in E\]
үшін теріс емес с
1
, с
2
сандапы табылып,
теңсіздігі орындалса, онда
\[\left\|{\vec{x}}\right\|_{1}\left\|{\vec{u}}\right\|\]
нормалары
эквивалентті деп аталады.
R
n
кеңістігінде анықталған 3 норма да эквивалентті.
§4. R
n
кеңістігіндегі скаляр көбейтінді.
Анықтама 1: Екі
\[{\mathcal Q}\,\]
және
\[\mathit{\mathcal{I}}\]
векторларының скаляр көбейтіндісі былай жазылады.
\[(a,b)\]
және ол мына формулалармен анықталады.
\[(a,b)=\sum_{i=1}^{n}a_{i}b_{i}\]
(1)
Скаляр көбейтінді үшін келесі қасиеттер орындалады.
\[\begin{array}{c}{{1/(a,b)=(b,a)}}\\ {{2)(a+b,c)=(a,c)+(b,c)}}\\ {{3)(d,b)=\lambda(a,b)}}\\ {{4)(a,b)^{3}~0,^{n}\;a\in R^{*}}}\end{array}\]
олай болса,
\[\left(a,a\right)=0\;\hat{\mathrm{U}}\;\;a=\theta\,;\]
Скаляр көбейтіндінің анықтамасынан
\[\|a\|={\sqrt{(a,a)}}\]
теңдігі келіп шығады.
Анықтама 2: Екі вектор
\[{\mathcal Q}\,\]
және
\[\mathit{\mathcal{I}}\]
ортогональ деп аталады
\[a\ \bot b\]
, егер
\[(a,b)=0.\]
Мысал: е
i
бірлік векторының координаттары қос-қостан ортогональды.
Шынында да
\[\begin{array}{c}{{e_{k}=\left(0,0,...,1,0,...,0\right)}}\\ {{e_{m}=\left(0,0,...,1,0,...,0\right)}}\end{array}\]
онда
\[\left(e_{k},e_{m}\right)=0^{*}0+...+1^{*}0+...+0^{*}1+0^{*}0+...+0^{*}0=0\]
Егер
\[a=(a_{1},a_{2},...,a_{n})\surd\qquad\]
вектор болса, онда
\[(a,e_{i})=a_{i}\]
демек
\[a=\hat{\sum_{i=1}^{n}}a_{i}e_{i}\]
жіктеуін мына түрде жазуға болады.
\[a=\sum_{i=1}^{n}(a,e_{i})_{i}\]
(2)
Егер
\[\|e_{i}\|=1\]
деп алсақ, үш өлшемді кеңістіктегідей
\[(a,e_{i})\]
скаляр көбейтіндіні
\[{\mathcal Q}\,\]
векторының
\[{\mathcal{C}}_{i}\]
бірлік векторына
проекциясын айтуға болады.
\[\forall a_{i}\ j_{i}\]
,
\[i={\overline{{1,n}}}\]
сандары үшін Коши-Буняковский
теңсіздігін мына түрде жазуға болады.
\[\sqrt{\frac{a}{\Delta}\sqrt{\frac{a}{\Delta}\left|{a_{k}\stackrel{\wedge\star}{\Lambda}b_{k}}\right|}}\;\;\leq\sqrt{\frac{a}{\Delta}\stackrel{\star}{a_{k}}\wedge}^{2}\;\approx\sqrt{\sum_{i=1}^{n}J_{k}^{2}}\]
Бұл теңсіздікті былай да жазуға болады.
теңсіздік скаляр көбейтіндінің қасиеттерінің бірін
сипаттайды. Екі вектордың скаляр көбейтіндісінің абсолют шамасы олардың нормаларының көбейтіндісінен асып кетпейді.
Скаляр көбейтіндінің анықтамасынан екі
\[{\mathcal Q}\,\]
және
\[\mathit{\mathcal{I}}\]
векторлар арасындағы бұрыш түсінігін енгізуге болады.
\[\left(3\right){\bf p}\ \left\vert\frac{\left(a,b\right)}{\left|\left|a\right|\right|\left|b\right|}\right\vert\ \leq1\]
модулі 1-ден аспайтын
\[\textstyle\bigvee\]
санға косинусты теңестіруге болады.
\[j\;=\left[0;\pi\right]\]
Сондықтан
\[{\frac{\left(a,b\right)}{\left\|a\right\|\left\|b\right\|}}=\cos\phi\]
\[\mathcal{J}\]
шамасы деп
\[{\mathcal Q}\,\]
және
\[\mathit{\mathcal{I}}\]
векторларының арасындағы бұрышты айтамыз.
Сол себептен
Егер векторлар нөльдік болмаса, онда олардың ортогональдығы арасындағы бұрышты
\[j_{\mathbf{\delta}}=\frac{\pi}{2}\]
екендігін білдіреді.
II тарау.
§5. R
n
кеңістігіндегі сызықты функционал .
Анықтама 1: R
n
кеңістігінде
\[\int_{0}^{x}H_{\mathbf{\delta}}\]
функционал берілсін, егер де
\[\mathrm{\Gamma}_{\ a}\ \in R^{n}\]
векторы
\[{\mathcal{F}}(a)\]
нақты санына сәйкестендірілсе.
Олай болса
\[\int_{0}^{x}H_{\mathbf{\delta}}\]
функционал R
n
кеңістігін R кеңістігіне бейнелейді.
\[\int_{0}^{x}H_{\mathbf{\delta}}\]
функционал сызықты деп аталады, егер
\[\forall a\ \beta\]
сандары мен
\[a,b\in R^{n}\]
векторлары үшін келесі теңдік орындалса.
\[f\left(a\,a+b\,b\right)=a f\left(a\right)+\beta f\left(b\right)\]
(1)
Мысал 1: R
n
кеңістігіндегі
\[{}^{*}a=(a_{1},a_{2},...,a_{n})\]
векторын алайық.
\[f(a)=a_{1}\]
функционалын қарастырайық.
\[a,b\in R^{n}\]
үшін
\[{\mathcal{F}}(a)\]
-ның сызықты функционал болатынын көрсетейік.
1)
\[f(a a+b b)=a\,a_{1}+\beta b_{1}\]
2)
\[f(a)=a_{1}\]
,
\[f(b)\!=\!b_{1}\]
Онда мынау анық
\[f\left(a\,a+b\,b\right)=a f\left(a\right)+\beta f\left(b\right)\]
Мысал 2: R
n
кеңістігінде
\[\tilde{n}=\left(\tilde{n}_{1},\tilde{n}_{2},...,\tilde{n}_{n}\right)\]
тағайындалған вектор болсын.
\[{}^{*}\ a=(a_{1},a_{2},...,a_{n})\in R^{n}\]
векторын аламыз.
\[{\mathcal Q}\,\]
және
\[{\widetilde{\mathcal{U}}}\]
үшін
\[\left(\widetilde{\cal H},Q\right)\]
скаляр көбейтіндіні қарастырамыз.
\[f(a)=(c.a)\]
сызықты функционал екенін көрсету керек.
\[a,b\in R^{n}\]
үшін
\[f(a a+b b)=(c_{s}a a+b b)=\left(c_{s}a a\right)+\left(c_{1}b b\right)=a\left(c a\right)+b\left(c b\right)=a f(a)+\beta f(b)\]
Яғни
\[{\mathcal{F}}(A)\]
- сызықты функционал.
Мысал 3:
R
n
кеңістігінде
\[\displaystyle\mathbf{v}f\]
сызықты функционал болсын.
\[\mathbb{S}c\ \in R^{n}\]
және
\[{}^{n}\,a\ \in R^{n}\]
үшін
\[f(a)=(c.a)\]
екенін көрсету керек.
Шынында да
\[{\mathcal{C}}_{i}\]
-бірлік вектор. Онда
\[{}^{*}\ a=(a_{1},a_{2},...,a_{n})\in R^{n}\]
векторы үшін
\[a=\hat{\sum_{i=1}^{n}}a_{i}e_{i}\]
.
Онда
\[f(a)=f{\big(}a_{1}e_{1}+a_{2}e_{2}+\ldots+a_{n}e_{n}{\big)}=a_{1}f{\big(}e_{1}{\big)}+a_{2}f{\big(}e_{2}{\big)}+\ldots+a_{n}f{\big(}e_{n}{\big)}\]
.
\[f(e_{i})=c_{i}\]
деп белгілесек,
\[\tilde{n}=\left(\tilde{n}_{1},\tilde{n}_{2},...,\tilde{n}_{n}\right)\]
болады. Онда
R
n
кеңістігіне тиісті
\[\mathcal{Y}\]
сызықты функционал үшін, R
n
кеңістігіне тиісті
\[\tilde{n}=\left(\tilde{n}_{1},\tilde{n}_{2},...,\tilde{n}_{n}\right)\]
вектор бар болады да
\[f(a)=(c.a)\]
(2)
2 және 3 мысалдардан (2) теңдеу R
n
кеңістігіндегі сызықтық функционалдың жалпы көрінісі болады.
Анықтама 2:
R
n
кеңістігінде анықталған сызықты функционалдың нормасы деп
\[\|f\|=\operatorname*{sup}_{|a|\geq}|f(a)\]
(3)
санын айтамыз.
R
n
кеңістігінде анықталған сызықты функционалды скаляр көбейтінді түрінде жаза алатынымызды ескерсек
\[f(a)=(c.a)\]
Онда
\[\|f\|=\|c\|\]
екендігін көрсетейік.
Расында да
\[\left\|f\right\|\ \leq\left\|C\right\|\]
теңсіздігі келіп шығады. Ары қарай
\[\scriptstyle a=c\]
деп алсақ, онда
\[f(c)=(c.c){=}\|c\|^{2}=\|c\|_{x}\|\]
бұдан
§6. R
n
кеңістігіндегі сызықты оператор .
Сызықты оператор анықтамасы.
Анықтама 1
: Сызықты оператор деп R
n
кеңістігін
R
m
кеңістігіне бейнелейтін
\[\textstyle\bigvee\]
мына
\[{\cal A}\models{\cal\theta}^{n}\to\mathit{\cal\theta}^{m}\]
бейнелеуді айтамыз.
Ол мына шарттарды қанағаттандырады.
1)
\[A{\bigl(}x+y{\bigr)}=A x+A y,^{*}x,y\in R^{n}\]
2)
\[A(a x)\!=\!a\,A x,^{\nu}\alpha\ \hat{1}\ R,x\in\!R^{\mu}\]
және 2) шарттарды біріктіріп келесі түрде жазуға болады.
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
Ұқсас жұмыстар
Гильберт кеңістігі: скаляр көбейтінді, Грам-Шмид ортогоналдануы және толықтық мысалдары Евклидтік кеңістік: анықтама, скаляр көбейтінді, норма және ортонормаланған базис Евклид және Гильберт кеңістіктері: скаляр көбейтінді, норма, ортогоналдық жүйелер мен базис Евклид кеңістігінің теориясы: скаляр көбейтінді, норма, ортонормалданған базис және изоморфизм Сызықты кеңістіктер: анықтамалар, нормаланған және метрикалық құрылымдар, сызықты операторлар Векторлық алгебра, көпмүшелер теориясы және дискреттік құрылымдар: скаляр көбейтінді, базис, түбірлер, ЕҮОБ/ЕКОЕ, қатынастар және бейнелеулер Сызықты, нормаланған және Гильберт кеңістіктері: операторлар теориясы және Штурм-Лиувилль операторы үшін компакт әдіс Үшінші ретті сызықты дифференциалды операторлардың ядролығы Жойылмалы эллиптикалық операторлар класының оң анықталуы Унитар кеңістіктер және сызықтық операторлар: түйіндес, өзін-өзі түйіндес операторлар мен полярлы жіктелу
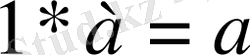
u, v>0, p, q>1 және
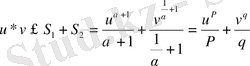
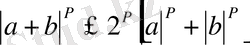
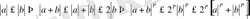
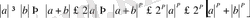
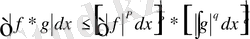
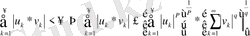
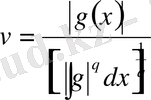
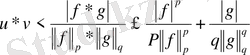
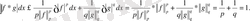
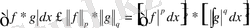
Минковский теңсіздігі .
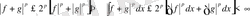
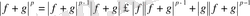
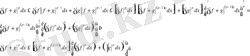
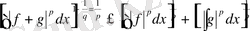
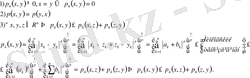
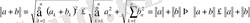
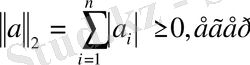
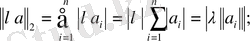
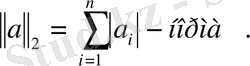
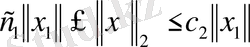
(3)
және
,
.
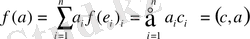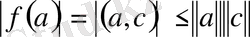теңсіздігінен
.
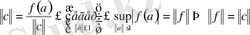