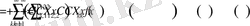Лаплас теңдеуі үшін төртбұрышта және дөңгелекте периодты, антипериодты және жоғарғы ретті туынды қатысқан бейлокал шеттік есептердің шешімділігі


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 65 бет
Таңдаулыға:
ЛАПЛАС ТЕҢДЕУІ ҮШІН КЕЙБІР БЕЙЛОКАЛ ЕСЕПТЕРДІҢ ШЕШІМДІЛІГІН ЗЕРТТЕУ
МАЗМҰНЫ
КІРІСПЕ
Зерттеу тақырыбынының көкейтестілігі. Қәзіргі заманғы авиациялық технологияда самолеттың материалдары көпқабатты пластиналардан құрылған [1, 2] . Мұндай пластинаны екі пластинадан туратын серпімді жүйе есебінде қарастыруға болады. Лагранж принципін қолдана отырып бұл моделді дифференциалдық теңдеулер жүйесіне келтіругеде болады. Осы теңдеулер қойылатын қосымша шарттар бейлокал шарттар болып табылады.
Дербес туындылы дифференциалдық теңдеулер үшін бейлокал есептер классикалық емес есептердің тобына кіреді. Лалпас теңдеуі үшін бейлокал шеттік есепті бірінші болып А. В. Бицадзе және А. А. Самарскийлердің 1969 жылы [3] жұмысында жарияланған. Эллипстік және басқа турдегі дифференциалдық теңдеулер үшін бейлокал есептердің шешілімділігін зерттеу мәселесіне көптеген әдебиеттер арналған. Бұл туралы мәліметтер А. Л. Скубачевскийдың 2007 және 2009 жылдары баспада жарық көрген [1, 2] әдебиеттерінде кеңінен көрсетілген.
Бейлокал есептерде ізделінді функцияның шекарадағы мәні оның есеп қарастырылатын областың ішіндегі мәнімен немесе ізделінді функцияның шекаранің бір бөлігіндегі мәні екінші бөлігіндегі мәнімен байланыста болады. Бұл есептерді моделдеу және бізге белгілі болған математикалық физиканың есептерін математикалық моделін құру кезінде эллипстік тектес теңдеулерді аламыз.
Эллипстік түрдегі теңдеулерге мысал ретінде Лаплас теңдеуін қарастыруға болады. Бұл теңдеу үшін әр түрлі шеттік және тағыда басқа есептерді қарастыруға болады.
Әдетте, қарастырылатын есептер корректі болуы қажет. Есептің корректілігі оның шешімі бар болуы, жалғыз болуы және орнықты болуын талап етеді.
Эллипстік түрдегі теңдеулер үшін классикалық шеттік есептерге Дирихле және Нейман есептері мысал болады . Бұл есептер классикалық болғанымен олар түрлі сыныптарға тиісте. Себебі Дирихле есебі шартсыз шешіледі, ал Нейман есебінің шешімі бар болуы үшін шекаралық функция үшін қосымша шарт талап етіледі, яғни Нейман есебі қосымша шартпен шешілетін есеп болып табылады. Бұл сияқты тұжырымдарды [4, 6] әдебиеттерден қарастыруға болады.
Қарапайым аймақтарда мұндай есептерді шешуде негізгі әдіс спектралдық әдіс болып табылады. Мұнда екінші ретті қарапайым дифференциалдық теңдеулер үшін спектралдық есеп келіп шығады. Бұл есептердің шешімі кейбір оператордың меншікті мәндері және меншікті функцияларын үйрену мәселесін туындатады. Егер қойылған есеп периодты немесе антипериодты (бейлокал есептердің қарапайым жағдайлары) есеп болса, онда есептің меншікті функциялары толық жүйе немесе Гильберт кеңістігінде базис құрайды.
Мұндай есептер шекаралық шартында жоғары ретті туынды қатысқан жағдайындатолық зерттелмеген. Сол себептен осы сияқты мәселені шешу актуалды мәселе болып табылады.
Дипломдық жұмыста Лаплас теңдеуі үшін төртбұрыш және дөнгелек сияқты арнайы областарда бейлокал шеттік есептердің шешілімділігі зерттелінеді.
Нәтижелердің ғылыми жаңалығы . Бұл бағытта негізгі нәтижелер бірінші ретті шекаралық операторлар үшін алынған. Жоғары ретті операторлар үшін мұндай есептер толық қарастырылмаған.
Жұмыстың мақсаты мен міндеті. Лаплас теңдеуі үшін арнайы областарда бейлокал есептердің шешімділігін зерттеу. Негізгі міндеттеріне өтсек, спектралдық әдісті қолданып бейлокал шекаралық шарттарымен берілген есептердің шешімі бар, жалғыз болуы туралы теоремаларды дәлелдеу. Шешімнің интегралдық түрін алу.
Зерттеу әдістері. Бұл ғылыми жұмысты жүргізуде математикалық физика теңдеулері, математикалық талдау, функционалдық талдау, интегралдық теңдеулер әдістері қолданылады.
Дипломдық жұмыстың көлемі мен құрылымы. Дипломдық жұмыс кіріспеден, 2 тараудан, қорытындыдан және әдебиеттер тізімінен тұрады. Негізгі материал 63 бетпен берілген, 11 қолданылған әдебиеттер атаулары келтірілген.
Дипломдық жұмыстың негізгі нәтижелері:
Енді дипломдық жұмыста қарастырылған есептерді баяндауға өтейік.
Жұмыстың бірінші тарауы төртбұрышта периодты және антипериодты шарттарымен берілген бейлокал шеттік есептер зерттеуге арналған. Бірінші және екінші параграфтарда екінші ретті жай дифференциалдық теңдеулер үшін бейлокал есептердің меншікті мәндері мен меншікті функциялары зерттелінеді. Тараудың 1. 3 және 1. 4 параграфтарында Лаплас теңдеуі үшін төртбұрышта периодты және антипериодты шарттарымен берілген шеттік есептер зерттелінеді.
Есептердің қойылымы
1-Есеп
. Айталық
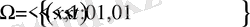 аралығында берілген
аралығында берілген
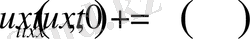
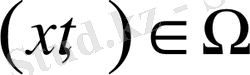 (0. 1)
(0. 1)
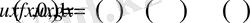
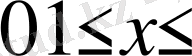 (0. 2)
(0. 2)

 (0. 3)
(0. 3)
есепті қарастырайық
1-есеп үшін негізгі нәтиже
1-Теорема.
Егер
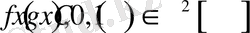 және
және

 шарттарын қанағаттандыратын (0. 1) - (0. 3) есебінің шешімі бар, жалғыз және
шарттарын қанағаттандыратын (0. 1) - (0. 3) есебінің шешімі бар, жалғыз және

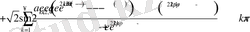
қатар түрінде өрнектеледі.
2-Есеп
. Айталық
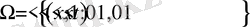 аралығында берілген
аралығында берілген
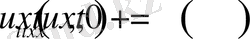
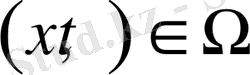 (0. 4)
(0. 4)
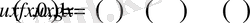
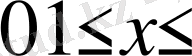 (0. 5)
(0. 5)

 (0. 6)
(0. 6)
2-есеп үшін негізгі нәтижесі
2-Теорема.
Егер
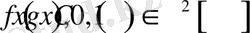 және
және

 шарттарын қанағаттандыратын (0. 4) - (0. 6) есебінің шешімі бар, жалғыз және
шарттарын қанағаттандыратын (0. 4) - (0. 6) есебінің шешімі бар, жалғыз және

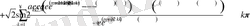
қатар түрінде өрнектеледі.
Екінші тарауда Лаплас теңдеуі үшін жоғарғы ретті туынды қатысқан бейлокал есептердің шешілімділігі зерттелінеді.
Тараудың бірінші параграфында Ω обласында гармониялық болған
u(x) функциясы үшін анықталған

түрінде берілген операторлардың қасиеттері зерттелінеді.
Мұнда С=(с 1 , с 2 , …, с m ) -векторы .
Тарауда қарастырылған негізгі есептер:
Айталық,
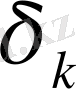 және
және

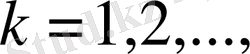 сандар тізбегі берілген болып, олар төмендегі шарттарды қанағаттандырсын:
сандар тізбегі берілген болып, олар төмендегі шарттарды қанағаттандырсын:
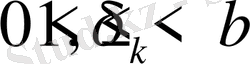
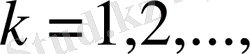
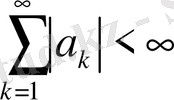 .
.
3-Есеп.
 облысында төмендегі берілген есепті қарастырайық :
облысында төмендегі берілген есепті қарастырайық :
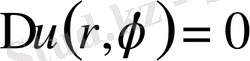 ,
,
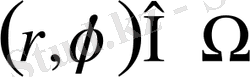 (0. 7)
(0. 7)
(0. 8)
мұнда
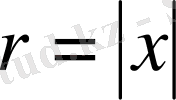 ,
,
 деп есептейміз.
деп есептейміз.
3-есеп үшін мынандай тұжырым орынды.
3-Теорема.
Егер
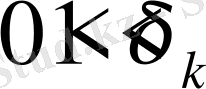 ,
,
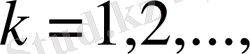 және
және
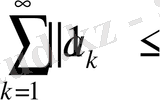 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
1)
жағдайда кез-келген үздіксіз
функциясы үшін
3-есептің шешімі бар және жалғыз болады.
- егержағдайда 1-есептің шешімі бар болуы үшін
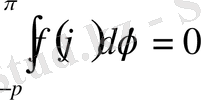 (0. 9)
(0. 9)
теңдіктің орынды болуы қажетті де жеткілікті.
Айталық,
 - дөнгелек,
- дөнгелек,
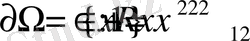 -шеңбер болсын.
-шеңбер болсын.
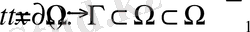 - диффеоморфизм (үздіксіз және кері бейнелеуі бар) және
- диффеоморфизм (үздіксіз және кері бейнелеуі бар) және
 ,
,
 -үздіксіз функция берілген болсын.
-үздіксіз функция берілген болсын.
4-Есеп.
Ω-облысында гармониялық болған,
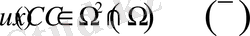 ,
,
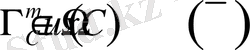 кластарына тиісті және
кластарына тиісті және
,
(0. 10)
шартын қанағаттандыратын
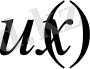 функциясын табу қажет.
функциясын табу қажет.
4-есеп үшін төмендегі тұжырым орынды.
4 - Теорема
. Айталық,
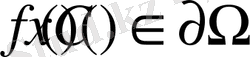 ,
,
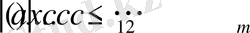 болсын.
болсын.
Онда
1) егер
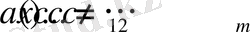 болса 4-есептің шешімі бар және жалғыз болады;
болса 4-есептің шешімі бар және жалғыз болады;
2) егер
 болса 4-есептің шешімі бар болуы үшін
болса 4-есептің шешімі бар болуы үшін
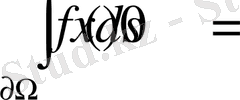
шарты орындалуы қажетті де және жеткілікті;
1. ЛАПЛАС ТЕҢДЕУІ ҮШІН ТӨРТБҰРЫШТА КЕЙБІР БЕЙЛОКАЛ ЕСЕПТЕРДІҢ ШЕШІМДІЛІГІН ЗЕРТТЕУ
1. 1 Жай дифференциалдық теңдеулер үшін периодты шеттік есептердің меншікті мәндері мен меншікті функциялары
Бұл параграфта екінші ретті жай дифференциалдық теңдеулер үшін кейбір бейлокал есептердің меншікті мәндері мен меншікті функциялары зерттелінеді. Осыған орай төмендегі есепті қарастырайық.
1. 1. 1-Есеп . Айталық, төмендегі
 (1. 1. 1)
(1. 1. 1)
 (1. 1. 2)
(1. 1. 2)
есептің (
 (х) ≠0) нөлге тең болмаған шешімін табу қажет болсын.
(х) ≠0) нөлге тең болмаған шешімін табу қажет болсын.
Мұндағы
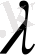 - тұрақты сан.
- тұрақты сан.
Бұл есептің
 (х) ≠0 шешімдері анықтама бойынша есептің меншікті функциялары, ал оларға сәйкес келетін
(х) ≠0 шешімдері анықтама бойынша есептің меншікті функциялары, ал оларға сәйкес келетін
 сандары есептің меншікті мәндері немесе меншікті сандары деп аталады.
сандары есептің меншікті мәндері немесе меншікті сандары деп аталады.
Енді (1. 1. 1), (1. 1. 2) - өрнекпен берілген теңдеудің
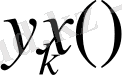 меншікті функциясын және
меншікті функциясын және
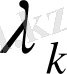 меншікті санын табайық.
меншікті санын табайық.
- теңдеудің сипаттамалық теңдеуі:

түрінде болады.
Осы
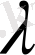 -параметріне сәйкес келетін келесі жағдайларды қарастырайық:
-параметріне сәйкес келетін келесі жағдайларды қарастырайық:
1)
 болсын делік. Онда сипаттамалық теңдеудің шешімі
болсын делік. Онда сипаттамалық теңдеудің шешімі
 болады.
болады.
Олай болса (1. 1. 1) -теңдеудің шешімі, яғни
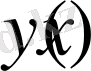 функциясы
функциясы
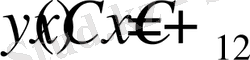 түрінде болады. Осы шешімге (1. 1. 2) - өрнектегі шарттарды қолданатын болсақ, онда бірінші шарттан
түрінде болады. Осы шешімге (1. 1. 2) - өрнектегі шарттарды қолданатын болсақ, онда бірінші шарттан
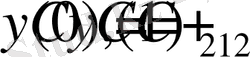
аламыз және
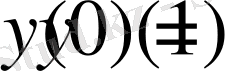 шартын пайдалана отырып
шартын пайдалана отырып
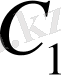 тұрақтысын табамыз.
тұрақтысын табамыз.

Бұдан
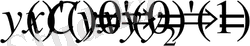
яғни
 тұрақтысы кез келген сан.
тұрақтысы кез келген сан.
Олай болса
 үшін шешім
үшін шешім
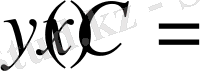 функциясы болады.
функциясы болады.
2)
Екінші жағдайда
 болсын. Онда
болсын. Онда
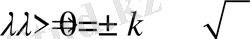 екені белгілі. Олай болса есептің шешімі болатын
екені белгілі. Олай болса есептің шешімі болатын
 функциясын мына
функциясын мына
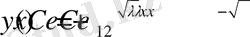
түрде іздейміз
Есептің берілген шарттарын қолдансақ, онда
 ,
,
 (1. 1. 3)
(1. 1. 3)
болады.
 функциясын туындылайтын болсақ, онда
функциясын туындылайтын болсақ, онда
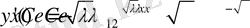
Енді
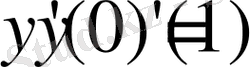 шартынан мынаны аламыз
шартынан мынаны аламыз
(1. 1. 4)
(1. 1. 3) және (1. 1. 4) теңдеулерден
 және
және
 тұрақтыларын табамыз
тұрақтыларын табамыз
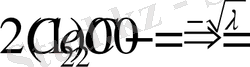
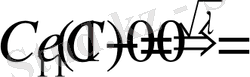
Олай болса
 үшін шешім
үшін шешім
 функциясы болады.
функциясы болады.
3)
Үшінші жағдайда
 болсын. Олай болса
болсын. Олай болса
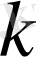 лар комплекс санға тең болады, яғни
лар комплекс санға тең болады, яғни
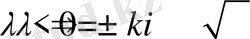 . Ізделінді функция:
. Ізделінді функция:
тең. (1. 1. 2) - өрнектегі шарттарды қолданып
 сандарын табайық
сандарын табайық

 (1. 1. 5)
(1. 1. 5)
Енді
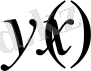 функциясынан
х
бойынша туындыласақ
функциясынан
х
бойынша туындыласақ
келесі шарттады қолдансақ, онда
Бұдан
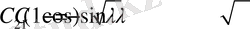 (1. 1. 6)
(1. 1. 6)
(1. 1. 5) және (1. 1. 6) теңдеулерден
 және
және
 тұрақтыларын табайық. (1. 1. 5) теңдеуін
тұрақтыларын табайық. (1. 1. 5) теңдеуін
 , (1. 1. 6) теңдеуін
, (1. 1. 6) теңдеуін
 тұрақтыларына көбейтіп қосайық,
тұрақтыларына көбейтіп қосайық,
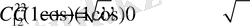
Олай болса келесі теңдеулер келіп шығады
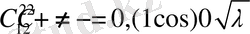
Бұдан

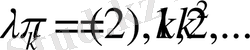 (1. 1. 7)
(1. 1. 7)
(1. 1. 7) меншікті мәндер (1. 1. 2) шарттарын қанағаттандырады.
Енді (1. 1. 5) теңдеуін
 , (1. 1. 6) теңдеуін
, (1. 1. 6) теңдеуін
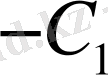 тұрақтыларына көбейтіп қосайық, онда
тұрақтыларына көбейтіп қосайық, онда
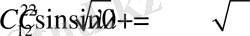
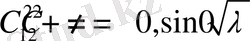
 (1. 1. 8)
(1. 1. 8)
(1. 1. 8) меншікті мәндер (1. 1. 2) шарттарын қанағаттандырмайды.
Сонымен (1. 1. 1), (1. 1. 2) есептен
 меншікті мәндері
меншікті мәндері
 . Ал меншікті функциясы жалпы түрде
. Ал меншікті функциясы жалпы түрде
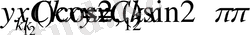
болды, енді жалғыз меншікті функциясын анықтаймыз. Ол үшін
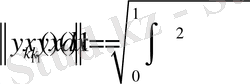
деп алып, С 1 тұрақтысының мәнін есептейміз

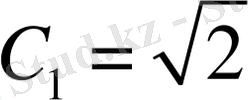
Келесі
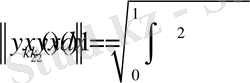
деп алып, С 2 тұрақтысының мәнін есептейміз

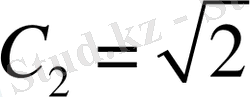
онда (1. 1. 1), (1. 1. 2) есептен
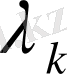 меншікті мәндері
меншікті мәндері
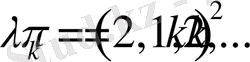 . Ал меншікті функциясы
. Ал меншікті функциясы
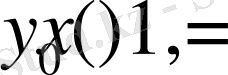
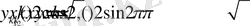
1. 2 Жай дифференциалдық теңдеулер үшін антипериодты шеттік есеп тердің меншікті мәндері мен меншікті функциялары.
Бұл параграфта екінші ретті жай дифференциалдық теңдеулер үшін шеттік шарттары антипериодты есептердің меншікті мәндері мен меншікті функциялары зерттелінеді. Осыған орай төмендегі есепті қарастырайық.
1. 2. 1-Есеп. Айталық, төмендегі
 (1. 2. 1)
(1. 2. 1)
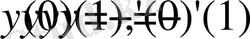 (1. 2. 2)
(1. 2. 2)
есептің (
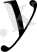 (х) ≠0) нөлге тең болмаған шешімін табу қажет болсын.
(х) ≠0) нөлге тең болмаған шешімін табу қажет болсын.
Мұндағы
 - тұрақты сан.
- тұрақты сан.
Бұл есептің
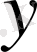 (х) ≠0 шешімдері анықтама бойынша есептің меншікті функциялары, ал оларға сәйкес келетін
(х) ≠0 шешімдері анықтама бойынша есептің меншікті функциялары, ал оларға сәйкес келетін
 сандары есептің меншікті мәндері немесе меншікті сандары деп аталады.
сандары есептің меншікті мәндері немесе меншікті сандары деп аталады.
Енді (1. 2. 1), (1. 2. 2) - өрнекпен берілген теңдеудің
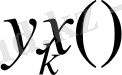 меншікті функциясын және
меншікті функциясын және
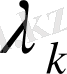 меншікті санын табайық.
меншікті санын табайық.
(1. 2. 1) теңдеудің сипаттамалық теңдеуі:

түрінде болады.
Осы
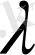 -параметріне сәйкес келетін келесі жағдайларды қарастырайық:
-параметріне сәйкес келетін келесі жағдайларды қарастырайық:
1)
 болсын делік. Онда сипаттамалық теңдеудің шешімі
болсын делік. Онда сипаттамалық теңдеудің шешімі
 болады.
болады.
Олай болса (1. 2. 1) -теңдеудің шешімі, яғни
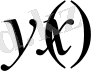 функциясы
функциясы
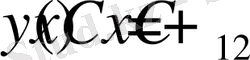 түрінде болады. Осы шешімге (1. 2. 2) - өрнектегі шарттарды қолданатын болсақ, онда бірінші шарттан
түрінде болады. Осы шешімге (1. 2. 2) - өрнектегі шарттарды қолданатын болсақ, онда бірінші шарттан
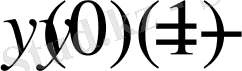
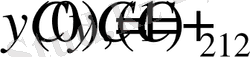
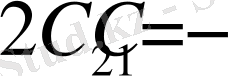
аламыз.
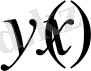 функциясынан туынды тапсақ
функциясынан туынды тапсақ
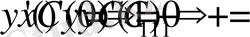
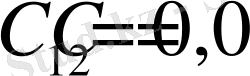
Олай болса
 үшін шешім
үшін шешім
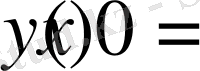 функциясы болады.
функциясы болады.
2)
Екінші жағдайда
 болсын. Онда
болсын. Онда
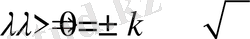 екені белгілі. Олай болса есептің шешімі болатын
екені белгілі. Олай болса есептің шешімі болатын
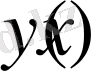 функциясын мына
функциясын мына
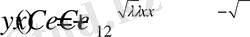
түрде іздейміз
Есептің берілген шарттарын қолдансақ, онда
 ,
,
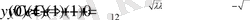 (1. 2. 3)
(1. 2. 3)
болады.
 функциясын туындылайтын болсақ, онда
функциясын туындылайтын болсақ, онда
 .
.
Енді
 шартынан мынаны аламыз
шартынан мынаны аламыз
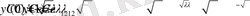
(1. 2. 4)
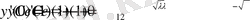
(1. 2. 3) және (1. 2. 4) теңдеулерден
 және
және
 тұрақтыларын табамыз
тұрақтыларын табамыз
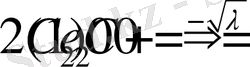
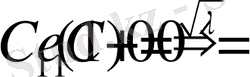
Олай болса
 үшін шешім
үшін шешім
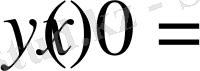 функциясы болады.
функциясы болады.
3)
Үшінші жағдайда
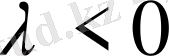 болсын. Олай болса
болсын. Олай болса
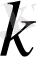 лар комплекс санға тең болады, яғни
лар комплекс санға тең болады, яғни
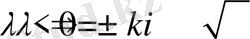 . Ізделінді функция:
. Ізделінді функция:
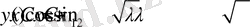
тең. (1. 2. 2) - өрнектегі шарттарды қолданып
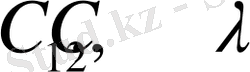 сандарын табайық
сандарын табайық

 (1. 2. 5)
(1. 2. 5)
Енді
 функциясынан
х
бойынша туындыласақ
функциясынан
х
бойынша туындыласақ
келесі шарттады колдансақ, онда
Бұдан
 (1. 2. 6)
(1. 2. 6)
(1. 2. 5) және (1. 2. 6) теңдеулерден
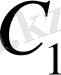 және
және
 тұрақтыларын табайық. (1. 2. 5) теңдеуін
тұрақтыларын табайық. (1. 2. 5) теңдеуін
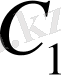 , (1. 2. 6) теңдеуін
, (1. 2. 6) теңдеуін
 тұрақтыларына көбейтіп қосайық,
тұрақтыларына көбейтіп қосайық,
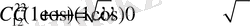
Олай болса келесі теңдеулер келіп шығады
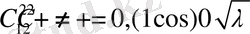
Бұдан

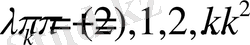 (1. 2. 7)
(1. 2. 7)
(1. 2. 7) меншікті мәндер (1. 2. 2) шарттарын қанағаттандырады.
Енді (1. 2. 5) теңдеуін
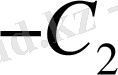 , (1. 2. 6) теңдеуін
, (1. 2. 6) теңдеуін
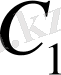 тұрақтыларына көбейтіп қосайық, онда
тұрақтыларына көбейтіп қосайық, онда
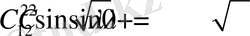
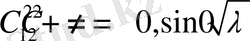
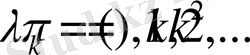 (1. 2. 8)
(1. 2. 8)
(1. 2. 8) меншікті мәндер (1. 2. 2) шарттарын қанағаттандырмайды.
Сонымен (1. 2. 1), (1. 2. 2) есептен
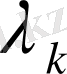 меншікті мәндері
меншікті мәндері
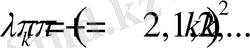 . Ал меншікті функциясы жалпы түрде
. Ал меншікті функциясы жалпы түрде
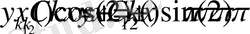
болды, енді жалғыз меншікті функциясын анықтаймыз. Ол үшін
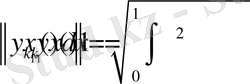
деп алып, С 1 тұрақтысының мәнін есептейміз

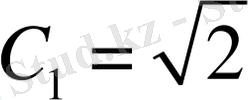
Келесі
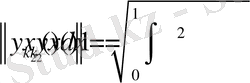
деп алып, С 2 тұрақтысының мәнін есептейміз

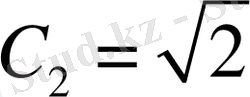
онда (1. 2. 1), (1. 2. 2) есептен
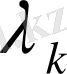 меншікті мәндері
меншікті мәндері
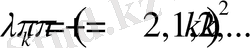 . Ал меншікті функциясы
. Ал меншікті функциясы
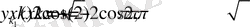
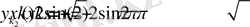
1. 3 Лаплас теңдеуі үшін төртбұрышта периодты шеттік есепті зерттеу.
1. 3. 1-Есеп
. Айталық
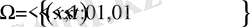 аралығында берілген
аралығында берілген
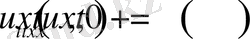
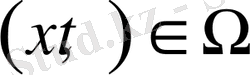 (1. 3. 1)
(1. 3. 1)
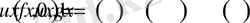
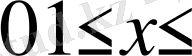 (1. 3. 2)
(1. 3. 2)

 (1. 3. 3)
(1. 3. 3)
есепті қарастырайық. Есептің шешімін екі функция көбейтіндісі, яғни
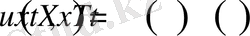 (1. 3. 4)
(1. 3. 4)
түрінде іздейміз. (1. 3. 4) функцияны (1. 3. 1) теңдеуіне қоятын болсақ, онда
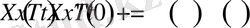
нәтижені аламыз. Соңғы теңдікті
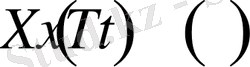 - ға бөліп жіберсек
- ға бөліп жіберсек
 (1. 3. 5)
(1. 3. 5)
теңдік шығады, мұндағы
 - тұрақты сан. (1. 3. 3) шарттарынан келесі теңдеулерді аламыз:
- тұрақты сан. (1. 3. 3) шарттарынан келесі теңдеулерді аламыз:
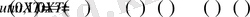
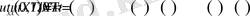
Енді (1. 3. 5) және соңғы шарттардан
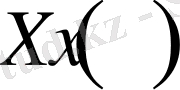 функциясы үшін
функциясы үшін

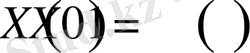
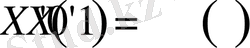 (1. 3. 6)
(1. 3. 6)
есебі шығады. Бұл алынған көмекші (1. 3. 6) - есеп 1. 1 - параграфтағы зерттелінген (1. 1. 1) - есеп болып табылады. Сол себептен (1. 3. 6) есебінің шешімі:
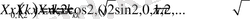
түріндегі функциялар болады.
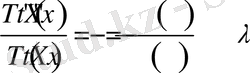
(1. 3. 5) теңдіктен
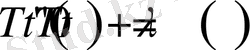 теңдеуінің шешімі
теңдеуінің шешімі
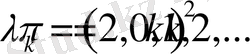 сандарына сәйкес түрде
сандарына сәйкес түрде
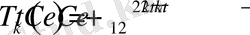
- бұл жалпы шешім. Олай болса (1. 3. 1) - (1. 3. 3) есептің шешімін
қатар түрінде іздеуге болады.
(1. 3. 2) - шартынан
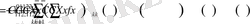
 функциясы
функциясы
 жүйе бойынша Фурье қатарына жіктелетін болып, сол қатар
жүйе бойынша Фурье қатарына жіктелетін болып, сол қатар

(1. 3. 7)
түрінде болсын, мұнда
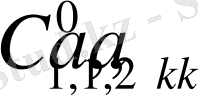 -
-
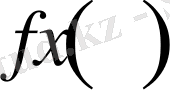 функциясының Фурье коэффициеттері. Онда
функциясының Фурье коэффициеттері. Онда

теңдіктерін аламыз.
Енді біз Фурье коэффициеттерін табу үшін (1. 3. 7) теңдіктің екі жағында
 көбейтіп,
көбейтіп,
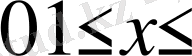 аралығында интегралдаймыз. Нәтижеде
аралығында интегралдаймыз. Нәтижеде
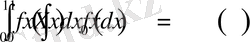
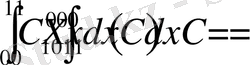


Осы табылған коэффициенттерді орнына қойсақ,
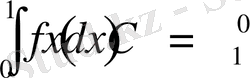
келіп шығады.
(1. 3. 7) теңдіктің екі жағын
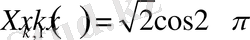 көбейтіп,
көбейтіп,
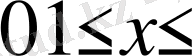 аралығында интегралдап нәтижесінде
аралығында интегралдап нәтижесінде
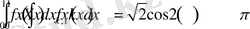
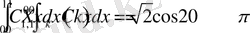

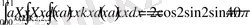
Бұдан табылғандарды орнына қойсақ,
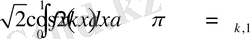
келіп шығады.
Сол сияқты (1. 3. 7) теңдіктің екі жағында
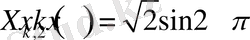 функциясына көбейтіп,
функциясына көбейтіп,
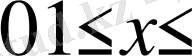 аралығында интегралдасақ
аралығында интегралдасақ
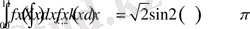
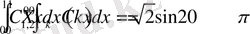
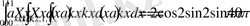

теңдіктерді аламыз.
Сонда табылғандарды орнына қойсақ,
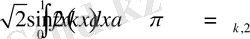
келіп шығады.
 функциясының Фурье коэффициенттері белгілі, келесі де біз
функциясының Фурье коэффициенттері белгілі, келесі де біз
 - тұрақтыларыны анықтауымыз керек. Бізде 4 белгісіз үшін екі теңдеу бар, қалған екі теңдеуді (1. 3. 2) шарттының
- тұрақтыларыны анықтауымыз керек. Бізде 4 белгісіз үшін екі теңдеу бар, қалған екі теңдеуді (1. 3. 2) шарттының
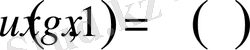 аламыз.
аламыз.
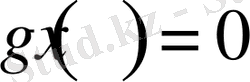 деп алып, дебес жағдайын қарастырайық, онда
деп алып, дебес жағдайын қарастырайық, онда
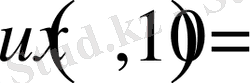
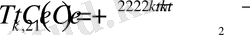
екені белгілі болса,
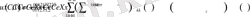 (1. 3. 8)
(1. 3. 8)
болады, онда жоғарыдағы амалдарды тағы қолданатын болсақ
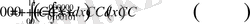
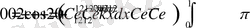
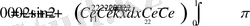
Онда
Енді біз табылған теңдеулер жүйесінен
 тұрақтыларын тапсақ жеткілікті.
тұрақтыларын тапсақ жеткілікті.
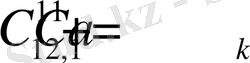
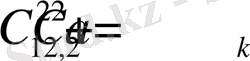
Біз бұл теңдеулер жүйесіні Maple жүйесінде шеше аламыз.
> restart;
> with(LinearAlgebra) :
> #k:=1:
lambda:=2*k*Pi;

> A:=<<1100>, <0011>, <exp(lambda) exp(-lambda) 00>, <00exp(lambda) exp(-lambda) >>;

> Determinant(A) :evalf(%) ;

> b:=<a1, a2, 0, 0>;
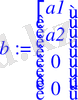
> A1:=A^(-1) ;

> x:=A1. b;

Яғни,

Онда (1. 3. 1) - (1. 3. 3) есептің шешімі

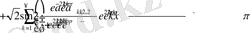
Мұнда,
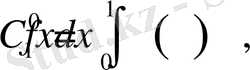
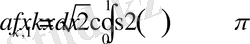
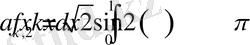
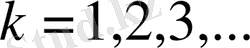
Біз
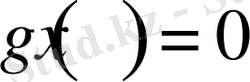 дербес жағдайын қарастырдық, енді жалпы түрде екінші есепті қарастырайық, яғни
дербес жағдайын қарастырдық, енді жалпы түрде екінші есепті қарастырайық, яғни
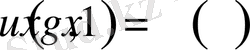 болсын, онда
болсын, онда
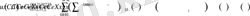 (1. 3. 8)
(1. 3. 8)
болады, онда жоғарыдағы амалдарды тағы да орындайтын болсақ
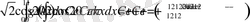
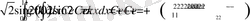
Онда
Табылған теңдеулер жүйесінен
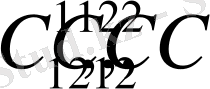 тұрақтыларын тапсақ жеткілікті.
тұрақтыларын тапсақ жеткілікті.
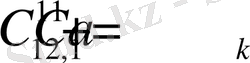
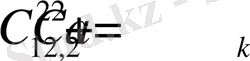
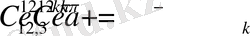
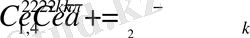
Мұнда,
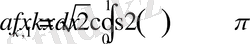 ,
,
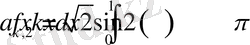 ,
,
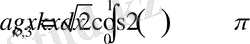 ,
,
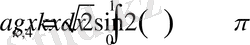
Біз бұл теңдеулер жүйесіні Maple жүйесінде шеше аламыз.
> restart;
> with(LinearAlgebra) :
> #k:=1:
lambda:=2*k*Pi;

> A:=<<1100>, <0011>, <exp(lambda) exp(-lambda) 00>, <00exp(lambda) exp(-lambda) >>;

> Determinant(A) :evalf(%) ;

> b:=<a1, a2, a3, a4>;
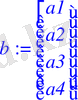
> A1:=A^(-1) ;

> x:=A1. b;

Яғни,

Онда (1. 3. 1) - (1. 3. 3) есептің шешімі



Мұнда,
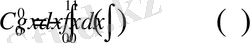
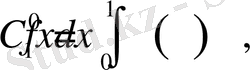
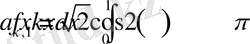 ,
,
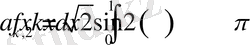
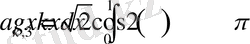
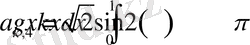
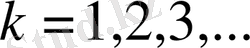
Сонымен (1. 3. 1) - (1. 3. 3) есебі үшін мына теореманы дәлелдедік.
Теорема 1. 3. 1.
Егер
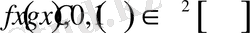 және
және

 шарттарын қанағаттандыратын (1. 3. 1) - (1. 3. 3) есебінің шешімі бар, жалғыз және
шарттарын қанағаттандыратын (1. 3. 1) - (1. 3. 3) есебінің шешімі бар, жалғыз және

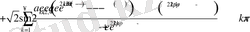
қатар түрінде өрнектеледі.
1. 4 Лаплас теңдеуі үшін төртбұрышта антипериодты шеттік есепті зерттеу.
1-Есеп
. Айталық
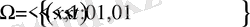 аралығында берілген
аралығында берілген
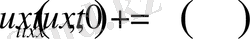
 (1. 4. 1)
(1. 4. 1)
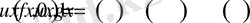
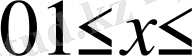 (1. 4. 2)
(1. 4. 2)

 (1. 4. 3)
(1. 4. 3)
есепті қарастырайық. Есептің шешімін екі функция көбейтіндісі, яғни
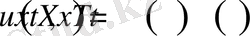 (1. 4. 4)
(1. 4. 4)
түрінде іздейміз. (1. 4. 4) функцияны (1. 4. 1) теңдеуіне қоятын болсақ, онда
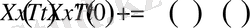
нәтижені аламыз. Соңғы теңдікті
 - ға бөліп жіберсек
- ға бөліп жіберсек
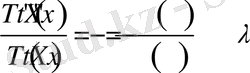 (1. 4. 5)
(1. 4. 5)
теңдік шығады, мұндағы
 - тұрақты сан. (1. 4. 3) шарттарынан келесі теңдеулерді аламыз:
- тұрақты сан. (1. 4. 3) шарттарынан келесі теңдеулерді аламыз:
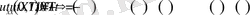
Енді (1. 4. 5) және соңғы шарттардан
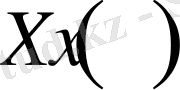 функциясы үшін
функциясы үшін

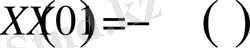
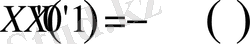 (1. 4. 6)
(1. 4. 6)
есебі шығады. Бұл алынған көмекші (1. 4. 6) - есеп 1. 1 - параграфтағы зерттелінген (1. 1. 1) - есеп болып табылады. Сол себептен (1. 4. 6) есебінің шешімі:
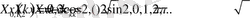
түріндегі функциялар болады.
(1. 4. 5) теңдіктен
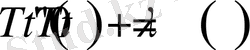 теңдеудің шешімі
теңдеудің шешімі
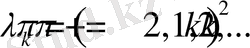 сандарына сәйкес түрде
сандарына сәйкес түрде
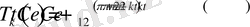
- бұл жалпы шешім. Олай болса (1. 4. 1) - (1. 4. 3) есептің шешімін
қатар түрінде іздеуге болады.
(1. 4. 2) - шартынан
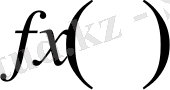 функциясы
функциясы
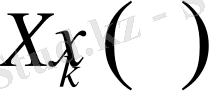 жүйе бойынша Фурье қатарына жіктелетін болып, сол қатар
жүйе бойынша Фурье қатарына жіктелетін болып, сол қатар
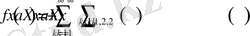
(1. 4. 7)
түрінде болсын, мұнда
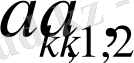 -
-
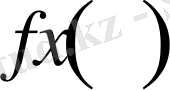 функциясының Фурье коэффициеттері. Онда
функциясының Фурье коэффициеттері. Онда

теңдіктерін аламыз.
Енді біз Фурье коэффициеттерін табу үшін (1. 4. 7) теңдіктің екі жағында
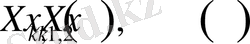 көбейтіп,
көбейтіп,
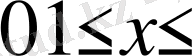 аралығында интегралдаймыз.
аралығында интегралдаймыз.
(1. 4. 7) теңдіктің екі жағын
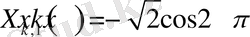 көбейтіп,
көбейтіп,
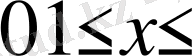 аралығында интегралдап нәтижесінде
аралығында интегралдап нәтижесінде


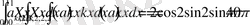
Бұдан табылғандарды орнына қойсақ,
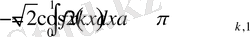
келіп шығады.
Сол сияқты (1. 4. 7) теңдіктің екі жағында
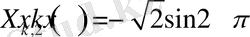 функциясына көбейтіп,
функциясына көбейтіп,
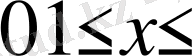 аралығында интегралдасақ
аралығында интегралдасақ
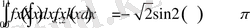
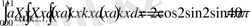

теңдіктерді аламыз.
Сонда табылғандарды орнына қойсақ,
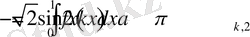
келіп шығады.
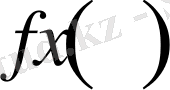 функциясының Фурье коэффициенттері белгілі, келесі де біз
функциясының Фурье коэффициенттері белгілі, келесі де біз
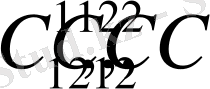 - тұрақтыларыны анықтауымыз керек. Бізде 4 белгісіз үшін екі теңдеу бар, қалған екі теңдеуді (1. 4. 2) шарттының
- тұрақтыларыны анықтауымыз керек. Бізде 4 белгісіз үшін екі теңдеу бар, қалған екі теңдеуді (1. 4. 2) шарттының
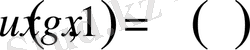 аламыз.
аламыз.
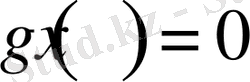 деп алып, дербес жағдайын қарастырайық, онда
деп алып, дербес жағдайын қарастырайық, онда
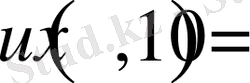
екені белгілі болса,
 (1. 4. 8)
(1. 4. 8)
болады, онда жоғарыдағы амалдарды тағы қолданатын болсақ

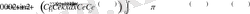
Енді біз табылған теңдеулер жүйесінен
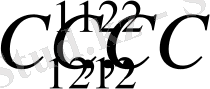 тұрақтыларын тапсақ жеткілікті.
тұрақтыларын тапсақ жеткілікті.
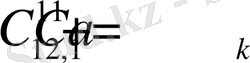
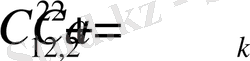
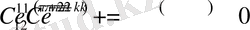
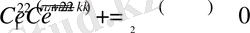
Біз бұл теңдеулер жүйесіні Maple жүйесінде шеше аламыз.
> restart;
> with(LinearAlgebra) :
> #k:=1:
lambda:=Pi+2*k*Pi;
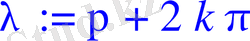
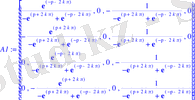
> A:=<<1100>, <0011>, <exp(lambda) exp(-lambda) 00>, <00exp(lambda) exp(-lambda) >>;
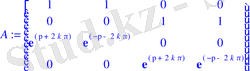
> Determinant(A) :evalf(%) ;

> b:=<a1, a2, 0, 0>;
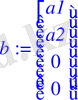
> A1:=A^(-1) ;
> x:=A1. b;
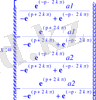
Яғни,


Онда (1. 4. 1) - (1. 4. 3) есептің шешімі


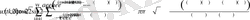
Мұнда,
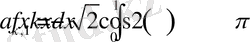
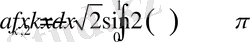
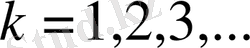
Біз
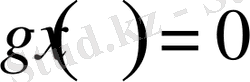 дербес жағдайын қарастырдық, енді жалпы түрде екінші есепті қарастырайық, яғни
дербес жағдайын қарастырдық, енді жалпы түрде екінші есепті қарастырайық, яғни
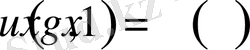 болсын, онда
болсын, онда
 (1. 4. 8)
(1. 4. 8)
болады, онда жоғарыдағы амалдарды тағы да орындайтын болсақ


Табылған теңдеулер жүйесінен
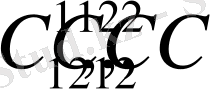 тұрақтыларын тапсақ жеткілікті.
тұрақтыларын тапсақ жеткілікті.
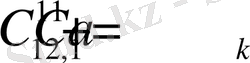
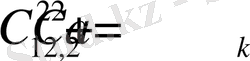
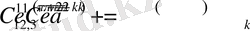
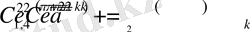
Мұнда,
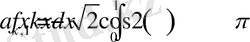 ,
,
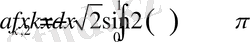 ,
,
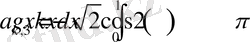 ,
,
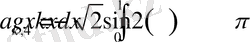
Біз бұл теңдеулер жүйесіні Maple жүйесінде шеше аламыз.
> restart;
> with(LinearAlgebra) :
> #k:=1:
lambda:=Pi+2*k*Pi;
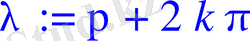
> A:=<<1100>, <0011>, <exp(lambda) exp(-lambda) 00>, <00exp(lambda) exp(-lambda) >>;
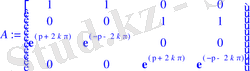
> Determinant(A) :evalf(%) ;

> b:=<a1, a2, a3, a4>;
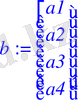
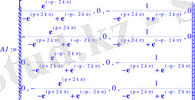
> A1:=A^(-1) ;
> x:=A1. b;

яғни,

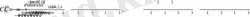
Онда (1. 4. 1) - (1. 4. 3) есептің шешімі
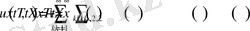
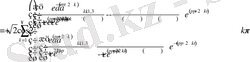
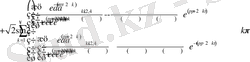

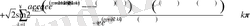
Мұнда,
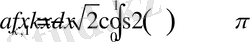 ,
,
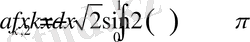
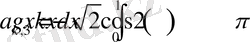
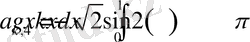
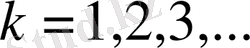
Сонымен (1. 4. 1) - (1. 4. 3) есебі үшін мына теореманы дәлелдедік.
Теорема 1. 4. 1.
Егер
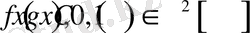 және
және

 шарттарын қанағаттандыратын (1. 4. 1) - (1. 4. 3) есебінің шешімі бар, жалғыз және
шарттарын қанағаттандыратын (1. 4. 1) - (1. 4. 3) есебінің шешімі бар, жалғыз және

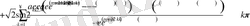
қатар түрінде өрнектеледі.
Мысал. (1. 3. 1) -(1. 3. 3) есеп үшін төмендегі мысалды қарастырайық.
Айталық, (1. 3. 1) -(1. 3. 3) есебінде
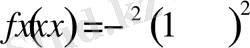 және
және
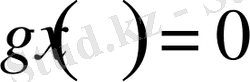 болсын.
болсын.
Бұл функциялар үшін теореманың шарттары, яғни
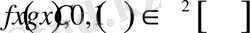 және
және

 шарттардың орынды болатыны айқын.
шарттардың орынды болатыны айқын.
Осы функцияларға сәйкес (1. 3. 1) -(1. 3. 3) есептің шешімін табайық.
> restart;
> f:=x->x^2*(1-x) ^2;
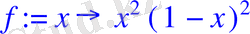
> f(0) ; f(1) ;


> diff(f(x), x) ;

> simplify(2*x*(1-x) ^2-2*x^2*(1-x) ) ;
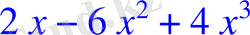
> f1:=x->2*x-6*x^2+4*x^3;
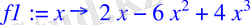
> f1(0) ; f1(1) ;


 шарттар орындалады.
шарттар орындалады.
> Int(f(x), x=0. . 1) =int(f(x), x=0. . 1) ;
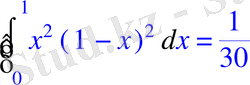
Int(sqrt(2) *f(x) *cos(2*k*Pi*x), x=0. . 1) =int(sqrt(2) *f(x) *cos(2*k*Pi*x), x=0. . 1) ;
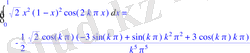
>Int(sqrt(2) *f(x) *sin(2*k*Pi*x), x=0. . 1) =int(sqrt(2) *f(x) *sin(2*k*Pi*x), x=0. . 1) ;
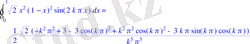
онда,
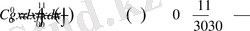
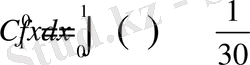
 ,
,

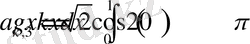
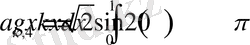
Егер
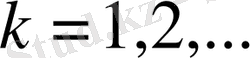 болса
болса
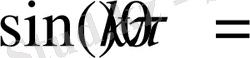 , ал
, ал
> restart;
> ak1:=(-sqrt(2) *cos(k*Pi) /2) *((-3*sin(k*Pi) +(k*Pi) ^2*sin(k*Pi) +3*k*Pi*cos(k*Pi) ) /((k*Pi) ^5) ) ;

> k:=1;
> print(`ak1`) ;

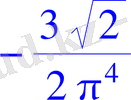
> k:=2;
> print(`ak1`) ;

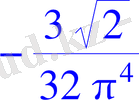
k:=3;
print(`ak1`) ;

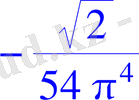
> k:=4;
> print(`ak1`) ;

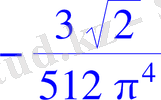
> restart;
> ak2:=(sqrt(2) /2) *((-(k*Pi) ^2+3-3*cos((k*Pi) ) ^2+(k*Pi) ^2*cos((k*Pi) ) ^2-3*k*Pi*sin(k*Pi) *cos(k*Pi) ) /((k*Pi) ^5) ) ;

> k:=1;
> print(`ak2`) ;


> k:=2;
> print(`ak2`) ;


> k:=25;
> print(`ak2`) ;


Сонымен
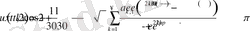

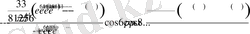
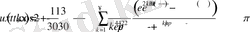
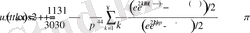
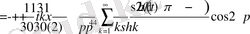
қатар түрінде өрнектеледі.
2 ЛАПЛАС ТЕҢДЕУІ ҮШІН ЖОҒАРҒЫ РЕТТІ ТУЫНДЫ ҚАТЫСҚАН БЕЙЛОКАЛ ЕСЕПТЕРДІҢ ШЕШІЛІМДІЛІГІ.
2. 1 Регуляр функциялар классында анықталған интегро-дифференциалдық операторлар және жалпыланған Дирихле есебі.
Бұл параграфта И. И. Бавринниң [11] жұмысында енгізілген, жеткілікті тегіс функциялар классында анықталған кейбір операторлардың қасиеттері және олардың шеттік есептерге қолданылуы мәселесін қарастырамыз.
Бұл параграфта келтірілетін мәліметтер көмекші мәліметтер болып, олар дипломдық жұмыстың екінші тарауында қарастырылатын негізгі есептер үшін қәжетті болады.
Айталық, Ω =
{х∈ R
2
: x <1}
-дөнгелек, ал
 =
{х∈ R
2
: x =1}
-шеңбер болсын.
=
{х∈ R
2
: x =1}
-шеңбер болсын.
Егер u(x) =u(x 1 , x 2 ) функциясы Ω облысында гармониялық функция болса, онда бұл функцияны [6]
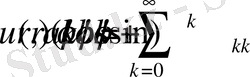
 (2. 1. 1)
(2. 1. 1)
көріністе жазып алуға болады, мұнда
r
=x, tgϕ=
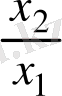 белгілеулері енгізілген.
белгілеулері енгізілген.
Бізге
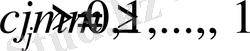 сандары берілген болсын. Осы сандарға сәйкес келетін
С
=(
с
1
, с
2
, …, с
k
) - векторын қарастырайық.
сандары берілген болсын. Осы сандарға сәйкес келетін
С
=(
с
1
, с
2
, …, с
k
) - векторын қарастырайық.
Алдымен m=1 болған, яғни С=с 1 болатын жағдайдан бастаймыз.
Осы С - тұрақтысына сәйкес түрде Ω обласында гармониялық болған
u(x) функциясы үшін
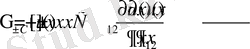
операторларын қарастырайық. Бұл операторлар С- тұрақтысы оң болған жағдайда И. И. Бавринның [2] жұмысында енгізілген.
Теорема 2. 1. 1 . Егер u(x) функциясы Ω облысында гармониялық болса, онда
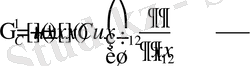
функциясыда Ω облысында гармониялық болады.
Дәлелдеу : Радиусы r=xболған шеңберге сыртқы өткізілген нормал векторы бағыты бойынша туынды

теңдікпен анықталады.
Онда
 операторын
операторын
 (2. 1. 2)
(2. 1. 2)
түрінде жазып алуға болады.
Егер u(x) функциясы Ω дөнгелекте гармониялық функция болса, онда ол (2. 1. 1) қатармен өрнектеледі.
(2. 1. 1) теңдігімен анықталған қатарға
 операторын әсер еттірсек, онда
операторын әсер еттірсек, онда
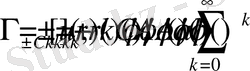 (2. 1. 3)
(2. 1. 3)
теңдігіне ие боламыз.
Шарт бойынша u(x) функцияcы Ω - дөнгелекте гармониялық, онда (2. 1. 2) қатар Ω облысының r=x<1 шартын қанағаттандыратын барлық нүктелерінде жинақты болады және оны жинақталу радиусы R=1 .
Онда
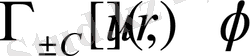 функцияларын анықтаушы (2. 1. 3) қатарыныңда жинақталу радиусыда
R=1
болады.
функцияларын анықтаушы (2. 1. 3) қатарыныңда жинақталу радиусыда
R=1
болады.
Нәтижеде (2. 1. 3) қатары r=x<1 облысында б3р 0алыпты жина0ты, сол себептен оның қосындысы Ω облысында гармониялық функция болады.
Теоерма дәлелденді.
Енді С=(с 1 , с 2 , …, с m ) -векторы берілген болсын деп есептеп

операторларын қарастырайық.
Теорема 2. 2. 2.
Егер
u(x)
функциясы Ω облысында гармониялық функция болса, онда
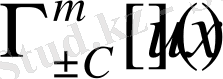 функцияларыда Ω да гармониялық болады.
функцияларыда Ω да гармониялық болады.
Дәлелдеу: 1. 1-теоерманың тұжырымы бойынша
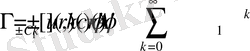 ,
,
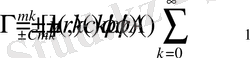 (2. 1. 4)
(2. 1. 4)
теңдіктері орынды болады.
Енді соңғы қатардың жинақталу радиусін табайық. Оның үшін Коши теоермасының нәтижесінен пайдаланамыз.
k индекстің жеткілікті үлкен мәндерінде

Онда

- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz