Күн жүйесі қозғалысы заңдылықтарын оқытудың әдістемелік ерекшеліктері

Кіріспе
I. Күн жүйесі қозғалысының теориялық негіздері
1.1 Күн жүйесі қозғалысының құрылымы
1.2 Планета қозғалысы
1.3 Аспан механикасы элементтері ... ... ..
ІІ.Күн жүйесі қозғалысы тақырыбын оқыту әдістемесі
2.1 Күн жүйесі құрылымы және планета қозғалысы
2.2 Күн жүйесі қозғалысы заңдылықтарын оқыту әдістемесі.. .
Қорытынды:
Әдебиеттер:..

Күн жүйесі деп динамикалық центрі болып табылатын Күнді айнала қозғалатын аспан денелерінің жиынтығын айтады. Күн жүйесіне өзінің серіктерімен 9 үлкен планета, 2300 аса кіші планеталар, көптеген метсориттік денелер (әр түрлі өлшемді тастар) және ұсақ шаң тозаң ағындары кіреді. Үлкен планеталар Күннен мынадай ретпен қашықтықта болады: Меркурий, Шолпан, Жер, Марс, Юпитер, Сатурн, Уран, Нептун және Плутон. Олар өлшемі Жермен өлшемдес шартәрізді қара денелер. Бұларды көбінесе планеталар д.а. Астероидтар пішіндері дұрыс емес формалы, өлшемдері жер диаметрі мен салыстырғанда 10,100,1000 есе кіші қатты денелер. Барлық кіші планеталар Юпитер мен Марс орбиталары аралығында өзіндік бір, астероидтар зонасы немесе белдеуі д.а., сақина құра Күнді айнала қозғалады. Юпитер, Сатрун, Уран, Нептун, Плутон, астероидтар белдеуінен тыс қозғалатын, сыртқы планеталар деп есептеледі. Ал Жер мен Марс, Меркурий, Шолпан ішкі планеталар. Күн мен жарықталынылатындықтан планеталар мен астероидтар көрінеді. Кіші планеталар ішіндегі ең үлкен деген астероидтың өзі тек қана телескоппен көрінеді, және жұлдыз сияқты жарқырауық нүкте сияқты көрінеді, сондықтан астероидтар деп аталған, яғни астероид деген сөз грекше жұлдыз тәрізді объекті деген сөз. Өте қашықтықтағы планеталар Плутон, Нептун, Уран да телескоппен көрінеді, себебі Күнмен жарықталынған әлсіз.

1. Воронцов Вельяминов Б.А., Попов П.И., Куницкий Р.В. Астрономия,
М Просвещение 1977.
2. Перельман Я.И. Занимательная астрономия 7 - 96 б.,155 - 165 б.
М. Наука, 1976
3. Климешин И.А. Астрономия наших дней, 78 - 155 б. М. Наука 1980.
4. Еремеев А. И. Астрономическая картина мира и её творцы,
М. Наука 1980.
5. Юрисов В. А. Учебно-методическое руководство по курсу «Астрономии» М.: Наука. 1980
6. Бакулин П.И. Кононович Э.В. Мороз З.М. Курс общей астрономии
М. Наука 1983.
7. Комаров В.Н. Новая занимательная астрономия, М. Наука , 1983
8. Дагаев М.М. и др. Астрономия, М Просвещение 1983.
9. Михайлов А.А Земля и её вращение. М. Наука, 1984.
10.Белонучкин В.Е. Кеплер, Ньютон и все-все-все... 33 - 58, 177 - 200 б.
М. Наука, 1990 , 5 - 49 бет
11. Воронцов-Вельяминов Б.А. Астрономия, 32 - 52 беттер.
Алматы Рауан, 1992
12.Дагаев М.М. Астрофизика, 5 - 27 б. М. Наука, 1994. 49 - 92 бет.,
155 - 165 бет.
13. Кононович Э. В., Мороз В. И. Общий курс астрономии. М.: Эдитор. 2001.

14. Клищенко А.П., Шупляк В.И. Астрономия.-М.: Новое знания. 2004ж

Пән: Астрономия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 46 бет
Таңдаулыға:

Физика және ФОӘ кафедрасы

Күн жүйесі қозғалысы заңдылықтарын оқытудың әдістемелік
ерекшеліктері

Аннотация
Қысқартылған сөздер мен терминдер

Кіріспе
I. Күн жүйесі қозғалысының теориялық негіздері
Күн жүйесі қозғалысының құрылымы
Планета қозғалысы
Аспан механикасы элементтері ... ... ..
ІІ.Күн жүйесі қозғалысы тақырыбын оқыту әдістемесі
Күн жүйесі құрылымы және планета қозғалысы
Күн жүйесі қозғалысы заңдылықтарын оқыту әдістемесі.. .
Қорытынды:
Әдебиеттер:..

І. Күн жүйесі қозғалысының теориялық негіздері

І.І. Күн жүйесі құрылымы.

Күн жүйесі деп динамикалық центрі болып табылатын Күнді айнала
қозғалатын аспан денелерінің жиынтығын айтады. Күн жүйесіне өзінің
серіктерімен 9 үлкен планета, 2300 аса кіші планеталар, көптеген
метсориттік денелер (әр түрлі өлшемді тастар) және ұсақ шаң тозаң ағындары
кіреді. Үлкен планеталар Күннен мынадай ретпен қашықтықта болады: Меркурий,
Шолпан, Жер, Марс, Юпитер, Сатурн, Уран, Нептун және Плутон. Олар өлшемі
Жермен өлшемдес шартәрізді қара денелер. Бұларды көбінесе планеталар д.а.
Астероидтар пішіндері дұрыс емес формалы, өлшемдері жер диаметрі мен
салыстырғанда 10,100,1000 есе кіші қатты денелер. Барлық кіші планеталар
Юпитер мен Марс орбиталары аралығында өзіндік бір, астероидтар зонасы
немесе белдеуі д.а., сақина құра Күнді айнала қозғалады. Юпитер, Сатрун,
Уран, Нептун, Плутон, астероидтар белдеуінен тыс қозғалатын, сыртқы
планеталар деп есептеледі. Ал Жер мен Марс, Меркурий, Шолпан ішкі
планеталар. Күн мен жарықталынылатындықтан планеталар мен астероидтар
көрінеді. Кіші планеталар ішіндегі ең үлкен деген астероидтың өзі тек қана
телескоппен көрінеді, және жұлдыз сияқты жарқырауық нүкте сияқты көрінеді,
сондықтан астероидтар деп аталған, яғни астероид деген сөз грекше жұлдыз
тәрізді объекті деген сөз. Өте қашықтықтағы планеталар Плутон, Нептун, Уран
да телескоппен көрінеді, себебі Күнмен жарықталынған әлсіз. Уранның
жарқырауы 6м, Нептундікі 8м жуық, Плутондікі 15м. Күнге жақынырақ
планеталар, яғни күн жарығымен молынан жарықталынатын, қарусыз көзбен де
көрінеді. Сондықтан ертедегі халыққа 5 планета белгілі болған: Меркурий,
Шолпан, Марс, Юпитер, Сатурн және олардың жұлдызды аспандағы байқалатын
қозғалысы оларды планета деп аталуға негіз болған(грекше планэтэс-адасқан).
Барлық планеталар мен астероидтар Күн айналасында тікелей деп
есептелетін Жердің қозғалыс бағытында қозғалады, Олар Күн (системасының)
жүйесінің бөлігі болып табылатын планеталар жүйесін құрады. Планеталар
жүйесінің радиусы 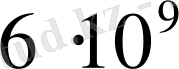км-ге жуық, Күннен Плутонға дейінгі аралық болып
табылады. Ол Күн мен Жердің арақашықтығынан 40 еседей үлкен. Планеталар
жүйесінің радиусы ең жақын деген жарық Центаврге дейінгі қашықтықтан
6900 есе кіші. Кеңістікте көрші планеталар бір-бірінен бірнеше ондаған
жүздеген миллион км қашықтықта болады. Планеталар аспан да зодиак шоқ
жұлдыздары бойымен эклиптика маңайында қозғалады. Бұны олардың
орбиталарының жер орбитасы жазықтығына көлбеуліктерінің өте аздығы
дәлелдейді. Сондықтан планеталар жүйесін жуықтап алғанда жазық деп
есептеуге болады. Плутон орбитасынан басқасы. Плутон орбитасы эклиптикаға
170-қа көлбеген 8.
Оларды бір тұтас система ретінде қарастыру себебіне ең алдымен үлкен
планеталарға тән бірсыпыра ортақ заңдылықтардың бар болуы негіз болып
табылады.
Барлық планеталар Күн айналасында тек қана бір бағытта айналады.
Барлық үлкен планеталардың орбиталары (Плутонды қоспағанда) мейлінше аз
эксцентристетке ие.
Барлық планеталардың орбитасының жазықтығы (Плутоннан басқа) эклиптика
жазықтығына өте аз көлбеулікте болады.
Барлық үлкен планеталардың барлығы дерлік (Уранды және Шолпанды қоспағанда)
өзінің орбиталдық қозғалыс бағытында өз остерінің айналасында айналады.
Көптеген серіктер Күн айналасындағы планеталардың қозғалыс бағытында өз
планеталарының маңайында дөңгелек орбита сызып айналады.
Планеталардың Күннен орташа орналасу ара кашықтығының шамасы Тициус - Бодэ
эмперикалық ережесімен анықталынатын мейлінше дұрыс қатар құрады :

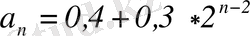
мұндағы n-планеталардың реттік номері 5. (Меркурийден Плутон
бағытында), ал өлшем бірлігі ретінде - Жердің Күнге дейінгі орташа ара
қашықтығы (яғни 1 астрономиялық бірлік) қабылданады. Планеталар
өздерінің физикалық сипаттамаларына қарай: ішкі ( немесе Жер тобы
планеталары деп аталатын) және сыртқы (Юпитер тобы немесе алып планеталар )
болып екі топқа бөлінеді. Ішкіге - астероидтар белдеуінің ішінде орналасқан
орбиталар бойымен қозғалатындар (Меркурий, Шолпан, Жер, Марс ), ал сыртқыға
- бұл белдеудің шектерінен шығып қозғалатындар (Юпитер, Сатурн , Нептун
және өзінің өлшемі жағынан мейлінше кем түсетін Плутон).
Екі әр түрлі топқа жататын планеталар массасы, өлшемі
тығыздығы, ішкі кұрылысы, химиялық құрамы және де серіктер саны бойынша
ажыратылады. Күн жүйесіне жататын табиғи серіктердің тек қана үшеуі ішкі
планеталар үлесіне келеді. Жер маңайында Ай, Марс жанындағы Фобы және
Деймос. Ал, енді Юпитердің он үш серіктері бар (олардың төрт ірілері
Галилейліктер деп аталады), Сатурнда - он, Уранда -бес, Нептунда - екі.

1.2. Планеталар қозғалысы.

Жердегі бақылаушыға планеталардың көрінерлік қозғалысы мейлінше
күрделі болып көрінеді. Егер Күн эклиптика бойымен өзгермейтін бағытта
(аспан сферасының тәуліктік айналысына қарсы) қозғалса, онда планеталар
аспан сферасында эклиптиканың маңайында орын ауыстыра отырып, бірде Күн қай
жаққа қозғалса, сол жаққа қарай (тура козғалыс деп аталады), бірде бұл
бағытқа қарама-қарсы бағытта (шегіне қозғалу) айнымалы жылдамдықпен
козғалады (1.1 сурет). Бұл жағдайда тура және шегіну қозғалыстарының
траекториялары беттеспейді. Осының нәтижесінде планеталар шоқжұлдыздар
ортасында ерекше иректер және тұзақтар сызады. Бұл жағдайда оның орны
тоқырау деп аталады.
Планеталардың тура және шегіне қозғалыстарының себебі планета
мен Жердің орбиталық сызықтық жылдамдықтарын салыстыра қарастыруда.
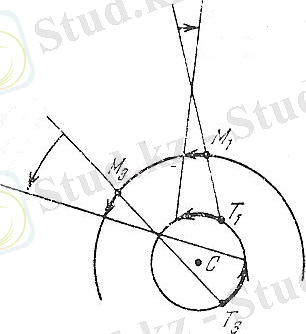
Жоғарғы планета (М3) (1.1-сурет) байланыс маңайында болса, онда
оның жылдамдығы Жердің (Т3) жылдамдығына қарама-қарсы жаққа
бағытталған болады. Жерден қарағанда планета тура бағытта қозғалып
бара жатқан сияқты, яғни оның нақты қозғалыс бағытында оңнан
солға қарай. Және де оның қозғалыс жылдамдығы артатын сияқты
болып көрінеді.
Жоғарға планета қарсы тұру маңайында (М1) болса, онда
планета мен Жердің жылдамдығы бір жаққа қарай бағытталады.
Бірақ Жердің сызықтық жылдамдығы Жоғарға планетаның
сызықтық жылдамдығынан үлкен, сондықтан Жерден қарағанда
планета қарама-қарсы бағытта қозғалып бара жатқан сияқты
көрінеді, яғни солдан оңға қарай шегіне қозғалады.
Осыған ұқсас төменгі планеталар (1.2-сурет) не себепті төменгі
байланыс маңайында (V1) жұлдыздар арасында шегіне
қозғалатындықтан, ал жоғарғы байланыс маңайында (V3 ) тура
қозғалатындығын түсіндіруге болады.
Аспан денелерін Жер бетінен бақылау шарты олардың Жер мен Күнге қатысты
орындарына байланысты. Планеталарды және Айдың Жерге және Күнге қатысты
өзара көрінерлік орналасуы конфигурациялары деп аталады.
1.2-1.3 суреттерде төменгі және жоғарғы планеталарға тән негізгі
конфигурациялар көрсетілген 6.

1.1 сурет Жоғарғы планеталар.
Планеталар мен Күннің эклиптика бойымен өлшенілетін бұрыштық ара
қашықтығы планеталардың элонгациясы делінеді. Күнге ең жақын планеталардың
- Меркурийдың және Шолпанның элонгациясы шектеулі. Сондықтан оларды не Күн
батуынан кейін көп кешікпей не оның шығу алдында

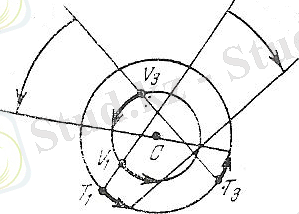
1.2 сурет.
Төменгі планеталардың тура және шегіне қозғалысы аз ғана бұрын
кездерде бақылауға болады. Көне заманда бұл планеталар төменгі планеталар
деп аталатын. Элонгациялары кез-келген мәндерді (0-ден 180° дейінгі)
қабылдай алатын планеталарды жоғары планеталар деп атайды. Оларға: Марс,
Юпитер, Сатурн, Уран, Нептун және Плутон жатады. Планеталардың элонгациясы
нольге тең болатын орыны планеталардың Күнмен тоғысуы делінеді. Жоғарғы
және төменгі тоғысулар бар.
Планеталардың тура қозғалысында байқалған қосылысты жоғарғы, ал
шегіну қозғалысында төменгі деп түсінеміз 14.
Күн жүйесі денелерінің аспандағы өзара көрінерлік орналасуын олардың
конфигурациясы деп атайды. Планеталардың конфигурациясын қарастырайық.
Планета мен Күннің эклиптика бойымен өлшенілетін бұрыштық арақашықтығы
планетаның элонгаиясы деп аталады.Планеталардың элонгациясы 0-ге тең
болатын орны планеталардың Күнмен тоғысуы деп аталады.Оны жоғары және
төменгі тоғысулар немесе байланыстар деп атайды.
Төменгі планеталар конфигурациялары
Меркурий мен Шолпанның элонгациясы шектеулі,сондықтан олар Күннің
маңайында болады.

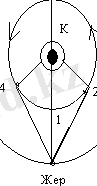
1.3-сурет

Суретте
1 – Планета Күн мен Жердің ортасында орналасқан конфигурацияны
төменгі байланыс деп атайды.
2 – Ең үлкен батыс элонгация
3 – Планета Күннің сырт жағында болғанда жоғары байланыс
4 – Ең үлкен шығыс элонгациясы деп атайды.
Планета орбитасының эллипс формалы болғандығынан ең үлкен элонгация
мәні тұрақты болмайды. Меркурийдің ең үлкен элонгациясы ,Шолпандыкі
аралығында өзгереді. Екі планета да Күннен алысқа кетпейді, сондықтан
түнде көрінбейді. Планеталардың элонгациясы 1800-қа жеткен жағдайдағы орны
қарсы тұру деп аталады. Егер элонгация 900 –қа тең болса,онда планета
квадратурада орналасты дейді.
Жоғары планеталар конфигурациялары
Элонгациясы кез – келген мәндерді қабылдай алатын яғни () қабылдай
алатын планеталар жоғары планеталар деп аталады. Планет 1-ші орында
болғанда конфигурация байланыс, 2-ші орында батыс квадратура, 3-ші орында
қарсы тұру, 4-ші орында шығыс квадратура деп аталады.

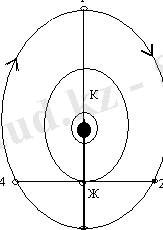
1.3 сурет

Сонымен планеталардың элонгациясы 180° жеткен жағдайдағы орыны қарсы
тұру деп аталады. Егер элонгациясы 90° тең болса, онда планета
квадратурада орналасты делінеді.
Біздерге өздігінен жарық шығармайтын денелерге жататын планеталар
жаркырап көрінеді, өйткені олар өздеріне түскен Күн сәулелерін
шағылыстырады. Сондықтан планеталардың, Жердің және Күннің өзара
орналасуына байланысты, планеталардың Айдікіне ұқсаған әр түрлі фазаларын
байқауға болады. Төменгі планеталардың фазалары жоғарғылардікінен өзгеше.
Төменгі тоғысуда төменгі планеталардың жарықталмаған жарты шары Жерге
қарайды. Ең үлкен элонгациясы ол бірінші ширекте байқалады. Содан кейін
планетаның ең үлкен келесі элонгациясында ол үшінші ширекте байқалады және
т.с.с.
Жоғарғы планеталардың Күнмен қосылысындағы фазасы түгелдей жарықталған
диск түрінде көрінеді. Квадратурада оның аздаған кемуі байқалынады. Толық
диск қарсы тұруда байқалады.
Планеталардың бақыланған қозғалысының күрделілігі олармен бірге Күнді
айналып қозғалатын Жердің орбиталық қозғалысына байланысты түсіндіріледі.
Планеталардың шын (яғни қозғалмайды деп алынған жұлдыздарыменен
байланысты санақ системасында қарастырылатын) қозғалысы Кеплер заңдарымен
сипатталады. Олардың біріншісі, планеталар Күнді фокустарының бірінде Күн
орналасқан эллипстік орбита бойымен айналып қозғалатынын тағайындайды.
Егер, осы фокуспен планетаның қашықтығы минимал болса, онда планета
перигелийде, егер де ол қашықтық максималь болса, онда планета
афелийде тұрады деп атайды (1.4 сурет). Егер полюсі Күн центрінде
орналасқан полярлық координаталарды планета орбитасының жазықтығында алсақ,
онда екінші реттік қисық теңдеуі түрінде Кеплердің бірінші занының
аналитикалық өрнегін беруге болады.

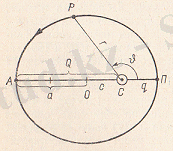
1.4 сурет
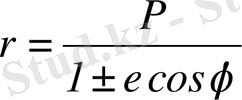(1)
мұндағы : 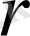- планетаның радиус векторы;
е - эксцентриситет;
Р - эллипс болған жағдайда эллипстің үлкен және кіші осі арқылы
бейнеленген мына түрдегі : 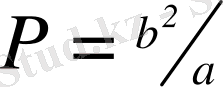екінші реттік қисықтың параметрі ;
а - планетаның Күннен орташа кашықтығы деп қарастыру керек екені
түсінікті. Бұл қашықтықты Жердің Күннен орташа қашықтығы бірлігінде
өрнектеу келісілген. Ұзындықтың осындай бірлігі астрономиялық бірлік
делінеді. Сонда ол:
млн. км
Кеплердің екінші заңы планетаның радиус-векторы бірдей уақыт
аралықтарында тең аудандар сызатындығын тағайындап,онын орбитальдық
қозғалыс жылдамдығын сипаттайды (1.5 сурет).

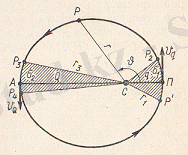
1.5 сурет

Бұл заңды не дифференциалдық:
(2)
не интегралдық түрде
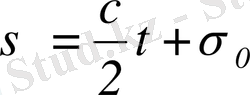немесе
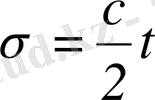(3)

түрде өрнектеуге болады. Мұндағы:
- қарастырған уақыт аралығында планета радиус-векторының сызып
өткен ауданы;
t - уақыт;
с - константасы аудандар тұрақтысы деп аталады. Бұл заңның
дифференциалдық түрін полярлық координаттарда бейнелеуге болады. Сонда (2)
мына түрге келеді:
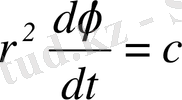(4)
Кеплердің үшінші заңы әр түрлі планеталардың сипаттамаларын
байланыстырады. Оның анықтамасы планеталардың сидерлік (яғни, жұлдыздық)
айналу периодтары квадраттарының қатынасы олардың үлкен жарты осі
кубтарының қатынасына тең болады.
Сонымен, 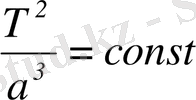яғни планетаның сидерлік айналу периоды квадраттың,
оның орбитасының үлкен жарты осінің кубына қатынасы тұрақты шама және
барлық планеталар үшін бірдей.
Кеплердің үшінші заңында сидерлік айналыс периоды бейнеленеді, ал енді
бақылаулар арқылы синодтық период анықталынады, осыған байланысты, осы
периодтардың өзара қатынасын анықтау қажеттілігі туады. Мұндай қатынас
синодтық теңдеумен тағайындалады 8.
Синодтық қозғалыс теңдеуі. Планеталардың бірдей аттас конфигурациялары
олардың орбиталарының әр түрлі нүктелерінде болады. Планеталардың бірінен
соң бірі болатын екі бірдей конфигурациясы уақыт аралығы S синодтық айналу
периоды деп аталады. Планеталардың орбиталарының бойымен айналу периоды
жұлдыздың жұлдыздық немесе сидерлік айналу Т периоды деп аталады. Егер
Жердің сидерлік айналу периодын Т0 деп белгілесек олардың арсында өзара
байланыс бар,оларды синодтық қозғалыс теңдеуі деп атайды.
Төменгі планетаны қарастырайық.

n, n0 - сәйкес планетаның және Жердің тәуліктік қозғалысы.
Жер мен планетаның бірдей конфигурциясы S синодтық период өткенде
болады,осы уақыт аралығынды Жер (1.6 сурет)

доға жүреді. Ал планета

төменгі планеталар үшін синодтық қозғалыс теңдеуі.

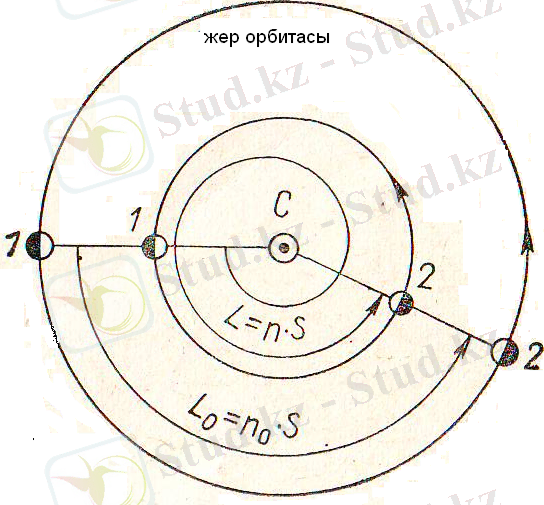
1.6 сурет
Аспан механикасы негіздері. Планеталардың қозғалыс заңдарынан кейін
мұндай қозғалыстың себебі не деген сұрақ тұрады. Бұл сұрақты шешу алдымен
денелердің қозғалыс заңдарын зерттеуді талап етеді. Аспан денелерінің
қозғалысын қарастыратын ғылым аспан механикасы деп аталады. Ол Ньютонның
ауырлық тартылыс заңына негізделген. Кеплер заңдары осы заңның салдарлары
болып табылады.
Ньютонның бүкіл әлемдік тартылыс заңы 1687 жылы жарық көрді.
Ньютон өзінің алдына мынадай сұрақ қойып, оны геометриялық жолмен
шешті. Планета бір фокусында Күн орналасқан эллипстік орбита бойымен
қозғалады, Күн тарапынан планетаға әсер ететін, эллипс фокусына қарай
бағытталған центрге тартқыш күш заңын анықтау қажет1.
Бұл есептің шешімі мынада:
Планетаға түсірілген күш орталық күш деп есептеледі. Кеплердің
екінші заңынан планетаның сектролық жылдамдығы тұрақты:

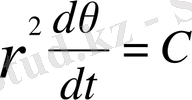
r -планетаның гелиоцентрлік радиус-векторы, Ө-нақты аномалия.
Бұл формуланы мына түрде жазуға болады:

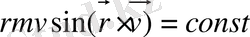
Бұдан сол планетаның Күнге қатысты импульс моментінің модулі:

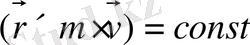
Кеплердің бірінші заңы бойынша планета орбитасы жазық қисық, олай болса
импульс моменті шамасы бойынша ғана емес, бағыты бойынша да тұрақты.

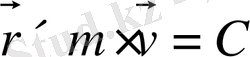
Импульс моменті теоремасы бойынша

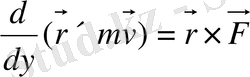
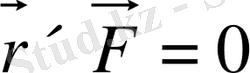
Бұдан планетаның қозғалысы кезінде барлық уақытта және
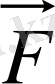векторлары колениарлы, яғни 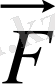күшінің әсер ету түзуі орталық дене (Күн)
арқылы өтеді, яғни күш орталық күш.
Осы күштің шамасын анықтау үшін кинетикалық энергияның
өзгеруі туралы теоремасын қолданамыз:

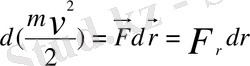
Мұндағы m-планета массасы, v-оның жылдамдығы, -гелиоцентрлік
радиус-векторы, 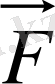-Күн тарапынан планетаға әсер ететін күш. Осы
теңдеуді шеше отырып, F-тың мынадай мәнін аламыз

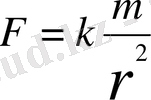
к - пропорционалдық коэффициент.
Күнге планеталардың тарапынан әсер ететін күшінің шамасы:

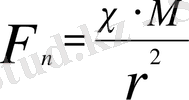
Мұндағы М-Күннің массасы, 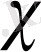- планетаға тән пропорционалдық
коэффициент.
Ньютонның үшінші заңына сәйкес

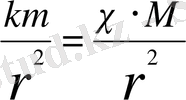
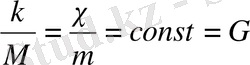
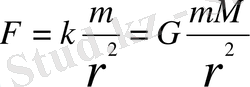
G - гравитациялық тұрақты деп аталады.

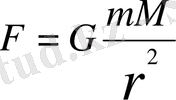
Кез-келген екі материялық бөлшек олардың массаларына тура пропорционал,
ара қашықтығының квадратына кері пропорционал күшпен бір-біріне тартылады.
Екі дене есебі. Табиғи және жасанды аспан денелерінң ілгерілемелі
қозғалысының негізгі заңдылықтарын өзара тартылыс күші әсерінен болатын екі
дене қозғалысын зерттеу нәтижесінде алуға болады.
Егер екі дененің массасы өзара бірдей болатын болса, онда мұндай есеп
жалпы екі дене есебі деп аталады, ал егер бір дененің массасын ескермеуге
болатындай болса, онда шектелген екі дене есебі деп аталады 8.
Практикада бір нүктенің қозғалысын координата басы басқа бір нүктедегі
системаға қатысты қарастырған жеткілікті. Сондықтан Sхуz системасын аламыз,
оның осьтерінің бағыты өзгермейді, және басы массасы М тартатын S
нүктесінде орналасқан болсын. Классикалық механика заңы бойынша m массалы
екінші Р нүктесі үшін Ньютонның теңдеуі былай жазылады:

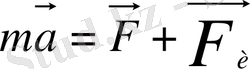
Мұндағы 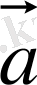-Р нүктесіндегі салыстырмалы үдеуі, 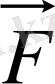-Ньютонның
тартылыс күші, -қандай да бір инерциалды санақ жүйесіне қатысты Sхуz
системасының үдемелі ілгерілемелі қозғалысынан болатын инерция күші.
Ньютонның тартылыс заңы бойынша
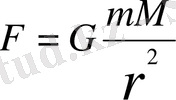Бұл күштің бағыты - бірлік векторы арқылы өрнектеледі.
S нүктесіне қарама-қарсы бағытталған F күші әсер етеді

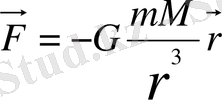
Онда координата системасының ілгерілемелі қозғалыс үдеуі 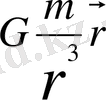. Осы
үдеуді Р нүктесінің m массасына көбейтіп инерция күшін анықтаймыз:

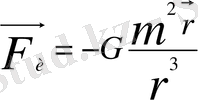
Енді табылған 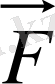және күштерінің мәнін орнына қойып,

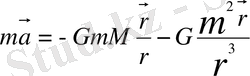
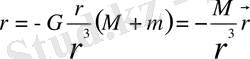(1) аламыз.
Мұндағы
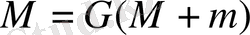
Шектеулі екі дене есебінде mM, олай болса
Кеплердің жалпы заңдары. Мына
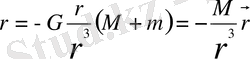(1)
теңдеудің шешімінен шығатын негізгі салдарларды қарастырамыз.
Дифференциялдық (1) теңдеудің мынадай интегралдары бар:
1) Аудан интегралы

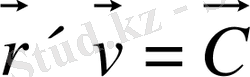(2)
С-импульс моментінің тұрақты векторы. С тұрақты болғандықтан дене
орбитасы жазық қисық болады. Егер осы жазықтықта полярлық r және θ
координаталарын енгізсек, онда аудан интегралын мына түрде жазуға болады:

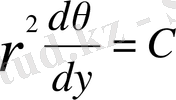(3)
Бұдан Кеплердің екінші заңы шығады.
2)Энергия интегралы
Қозғалыс теңдеуінен (1) энергияның сақталу заңы шығады:
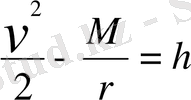
Мұндағы һ-қозғалыстағы дене массасына бөлінген толық механикалық
энергияға тең, тұрақты.
Жалпы түрде орбита теңдеуі (яғни (1) теңдеуінің шешімі)

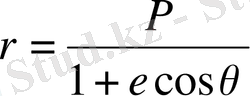(4)
Мұндағы е-эксцентриситет,θ-нақты аномалия.
Эксцентриситеттің шамасы толық энергия мәнімен анықталады және мынаған
тең

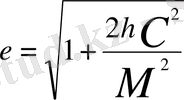(5)
h-қозғалыстағы дене массасына бөлінген толық механикалық энергия.
Фокальдық параметр
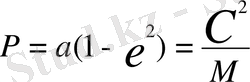(6)

(5) өрнектен траектоияның 3 түрі болатындығы көрінеді.
1)0e1 (h0) немесе (е=0 шеңбер)
2) e=1 (h=0) парабола
3)e1 (h0) гипербола
(4) формула Кеплердің жалпы бірінші заңының аналитикалық түрін
анықтайды.
Кеплердің үшінші жалпы заңы. Эллипстік қозғалыс үшін сидерлік Т
период пен α үлкен ось арасындағы байланысты табуға болады 6.
Эллипстің ауданы
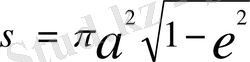, бұны радиус-вектор Т уақытта
сызады. (3) формуладан .
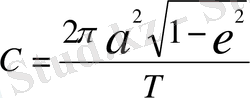Екінші жағынан (6) теңдеуден 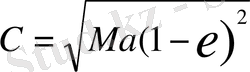. Бұларды теңестіріп
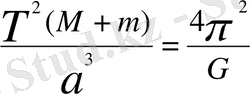аламыз.
Бұл Кеплердің үшінші жалпы заңы.
Егер М1 – Күннің массасы, m 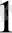- күнді айнала қозғалатын планета
массасы болса, ал М2 басқа бір системадағы планета массасы, ал m 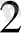оның
серігінің массасы болса, онда
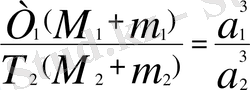егер m1M1 , m2M2 болса, онда
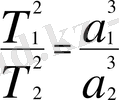Кеплердің үшінші заңы.
1.3. Аспан механикасының элементтері.

Әдетте, аспан механикасын Күн жүйесіндегі денелердің гравитациялық
өрісте қозғалыстарын зерттейтін астрономия бөлімі деп түсінеміз. Сонымен
қатар, ол объектіні зерттеуге қолдануға жарайтын арнайы бейімделген
механика саласы болады. Оның негізгі мәселелері ішінен тура және кері
мәселелерді айыра білу керек. Мәселенің бірінші типінің (яғни, тура)
мақсаты: берілген дененің сипаты бойынша денеге әсер етуші күштерді
анықтау. Кері мәселелердің (динамика негіздері ретінде қарастырылатын)
міндеті, егер оған әсер етуші күштер берілсе, дененің қозғалыс заңын
анықтауға болады 5.
Кеплердің тағайындаған планеталардың қозғалыс заңдарының негізінде
Ньютонның ашқан бүкіл әлемдік тартылыс заңы динамиканың тура мәселелер
шешіміне тамаша мысал бола алады. Кеплердің аналитикалық түрде (1), (3),
(4) өрнектелген зандарын қолдансақ, планетаға әсер етуші күштердің тендеуін
табамыз, (яғни Кеплер заңдарынан бүкіл әлемдік тартылыс заңын шығарып
аламыз). Осы мақсатпен полюсі Күн центріндегі планетаның қозғалыс
жазықтығына енгізілген полярлық координаталар жүйесінде Ньютонның екінші
заңының проекциясын жазамыз:

Ұзындығы тұрақты вектордан (соның ішінде бірлік векторынан) алынған
туынды, осы дифференциалдаушы векторға перпендикуляр және одан вектордың
бұрылу бұрышынан уақыт бойынша алынған туындыға тең көбейткішке
ажыратылған (өзгеше)

мұндағы: ,

вектор екендігін ескере отырып, планетаның полярлық координаталардағы
жылдамдығының теңдеуін оның анықтамасынан табамыз.

Сонымен,

анықтаймыз. Мұндағы: , және айнымалы үстіндегі нүкте
одан уақыт t бойынша алынған туындыны көрсетеді.
Сонда:
Сөйтіп,
(1)
(2)

Кеплердің аудандар заңын уақыт бойынша дифференциалдап-ақ
табамыз, ал олай болса:

(3)

1) теңдеудің сол жағын мына түрге келтіреміз:

(4)

Бұл (4) теңдікті ескергенде мынаны:

көрсетеді.

Сонымен, (1) теңдік мына төмендегідей түрге келеді:

Егер, орнына жаңа айнымалыны енгізсек, онда алдыңғы
теңдеу ықшамдалған түрге келеді:

Соңғы қатынасты Бинэ формуласы деп атайды. Бұған Кеплердің бірінші
заңының теңдеуін

қойсақ,

шығады.

айнымалы r - ге қайта оралғанда бұдан:

аламыз. (5)

Сөйтіп, планетаға әсер етуші күш планетаның массасына
пропорционал, ара қашықтығына кері квадраттық заңы бойынша өзгереді
және оның тек радиал құраушысы ғана болады. Минус таңбасы
бұл күштің таратушы күш екендігін көрсетеді 5.
(5) теңдіктің оң жағына енген коэффициентте планетаның
аудандар тұрақтысы С және орбитаның параметрі бар, демек, бұл
берілген планета үшін тұрақты шама болып келеді. Әр түрлі
планеталар үшін бұл тұрақты шама бірдей бола ма екен?
Әрине, бұл сұраққа жауап беру үшін Кеплердің үшінші заңына назар
аудару қажет (тек осы жерде ғана әр түрлі планеталардың қозғалыс
сипаттамалары бірге қарастырылады). Егер, Кеплердің аудандар заңының
интегралдык түрінде уақыт аралығын планетаның сидерлік айналу периоды Т
деп есептесек, онда ретінде белгілі тең эллипс ауданы деп
қарастыру керек. Осыдан:

тең болады.

Т периодтың табылған мәнін Кеплердің үшінші заңына қоямыз:

Сонда мына өрнек шығады:

Сонымен, Гаусс тұрақтысы деп аталынатын, тұрақты барлық
планеталар үшін бірдей. Сөйтіп, бұл тұрақтының мәні тек Күнге ғана
байланысты бола алады. Сондықтан, оны: деп белгілейміз. Әрі қарай
Ньютонның үшінші заңын ескерсек, планетаның Күнге әсер ету күші
табылғанға сәйкес былай өрнектеледі:

атап айтқанда

Мұндағы тең болу салдарынан екені шығады. Осы
қатынасты теңдіктің екі жағына енген сипаттамалар бір, тек қана бір денеге
қатынасы бар, деп есептеген жағдайдағы түрге келтірсек, былай болады:

Сөйтіп, енгізілген универсал константа гравитациялық
тұрақты делінеді.
Соңғы қатынасты ескерсек күш үшін іздеген теңдеу мына түрге келеді:

(6)

Тұңғыш рет тағайындалған заңның дұрыстығы Айдың центрге тарту үдеуінің
(6) формуласы бойынша есептелінген және "бақыланған" мәндерін салыстыру
арқылы тексеріліп жүзеге асырылады. Бақылау арқылы центрге тартылу үдеуін
белгілі теңдеу бойынша анықтауға болады:

мұндағы R - Жердің Айға дейінгі арақашықтығы;
t - Айдың Жерді айналу периоды; Бұл параметрлер бақылаулардан
анықталады.
Егер, М - Жердің, m - Айдың массасы деп санасақ, онда осы
үдеудің теориялық мәні (6) теңдіктен және Ньютонның екінші заңынан
шығады:

М - мәнін Жер шарының бетіндегі кез-келген дененің салмағын (m,g) (6)
теңдеуден шығатын, берілген жағдай үшін өрнекке теңестіру арқылы
анықтауға болады:

Бұдан

Осыған сәйкес:

және өзара салыстыруы олардың бір - біріне тең болуын
көрсетті, ал мұның өзі бүкіл әлемдік тартылыс заңы деп аталынған (6)
түрдегі тағайындалған заңның универсалды екендігін бірінші рет
дәлелдеді.
Бұл заңның ашылуы Ньютон үшін Ай қозғалысында байқалатын көптеген
ерекшеліктерді, Жердің полюстарда қысынқылығын, тасу, қайту және т. б.
түсіндіруге мүмкіндік береді.
Тамаша француз математигі және механигі Пьер Лаплас Ньютонның
тартылыс заңына сүйене отырып, 1798 жылы мейлінше массалы жұлдыздардан
жарықтың кете алмайтындығын атап қана қойған жоқ (демек, "біз үшін әлемдегі
жарық шығаратын ең үлкен денелер көрінбейтін болады...") сонымен қатар,
мұндай жұлдыздардың гравитациялық радиусы үшін дұрыс теңдікті ала
білді, сөйтіп "қара үнгірлер" ("черные дыры") деген ұғымды алдын ала болжап
таңқалдырды. Ньютон динамиканың тура есептерінің шешімдеріне ие бола
отырып, ол қарапайым түрде қойылған екі дене есептері деп аталынған кері
есептің шешіміне кірісті.
Сөйтіп, бүкіл әлемдік тартылыс заңы белгілі деп есептеп, планетаның
Күннен басқа барлық денелермен өзара әсері ескерілмейді деген болжам
шектеу жасай отырып, қарастырылып отырған осы планетаның орбитасының
формасын іздейміз. Планетаның қозғалысы Күнмен байланысты санақ системасына
қатысты қарастырылады. Күн кеңістікте ілгерлемелі қозғалыста болады деп
жорамалдайды.
Планета мен Күнді m және М массаларға сәйкес Р және S материалдық
нүктелер ретінде есептеп, планетаның салыстырмалы қозғалысының теңдеуін
мына түрде жазамыз:

мұндағы: -- Күннің тарабынан планетаға әсер етуші күш;
- Күнмен байланыстағы санақ жүйесінің үдеуі.
Ньютонның екінші заңы бойынша Күннің үдеуі оған әсер етуші
күшпен және оның массасы шамасымен:

анықталады. Сондықтан алдыңғы теңдеу мына төмендегідей түрде болады:

өрнектеледі.

Жоғарыда көрсетілгендей планетаға әсер етуші күштің
тангенциал
- құраушысы жоқ. Сондықтан, . Бірақ, Бинэ
формуласын қанағаттандырады. Олай болса, соңғы теңдеу мына түрге
келеді:

ал бұл бүкіл әлемдік тартылыс заңы бойынша екінші ретті
дифференциалдық теңдеуге келтіріледі:

(2)
Бұл біртекті емес сызықты дифференциалды теңдеудің жалпы
шешімі - жалпы біртектінің және оң жақ бөлігінің
тұрақты болуы салдарынан оңай табылатын біртекті емес

теңдеулердің екі шешімдерінің қосындысынан тұрады. Сонымен, жалпы
интегралды (7) мына түрде табамыз:

Егер, тұрақты мына шамаларды енгізсек: ;
онда алатынымыз:

Осыдан:

және: (8)

шығады . Алымында тұрған оң таңбалы тұрақтыны Р арқылы , ал - дeri
коэффициентті арқылы белгілеп мынаны аламыз:

(9)

Бұл екінші ретті қисықтың теңдеуі болып саналады. Егер, осы
қисықтың төбесі және оның фокусы арқылы өтетін осы оське
катысты қисық симметриалы болса, онда қисықтың түрін
анықтамайтын, тек оның полярлық оське қатысты бағытталуын сипаттайтын
тұрақты ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.