Меншіксіз интегралдар (I және II түрлері), олардың жинақтылығы және жиындар мен функциялар бойынша практикалық тапсырмалар


I-тектi меншiксiз интегралдар
Шексiз:
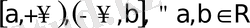 және
және
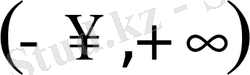 аралықтарынының бiрiнде үзiксiз
аралықтарынының бiрiнде үзiксiз
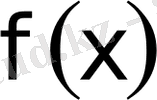 функциясы қаралады. Алғашқы екi жағдайда сәйкес жоғарғы және төменгi шектерi айнымалы анықталған интегралдар
функциясы қаралады. Алғашқы екi жағдайда сәйкес жоғарғы және төменгi шектерi айнымалы анықталған интегралдар
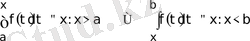
бар болады. Олардың шектерi
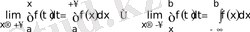 (4. 1)
(4. 1)
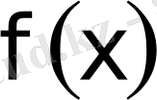 функциясынан алынған шектерi шексiз
(I-тектi) меншiксiз интеграл
деп аталады.
функциясынан алынған шектерi шексiз
(I-тектi) меншiксiз интеграл
деп аталады.
Егер (4. 1) - дiң сол жақтарындағы шектер бар және нақты сандар болса, онда оларға тең меншiксiз интегралдар да бар және жинақты деп аталады. Қарсы жағдайда (шектер жоқ не
 -ке тең) (4. 1) - мен анықталатын меншiксiз интегралдар жинақсыз (тарқамалы) делiнедi.
-ке тең) (4. 1) - мен анықталатын меншiксiз интегралдар жинақсыз (тарқамалы) делiнедi.
Бүкiл сандық осьте үзiксiз функция үшiн шектерiнiң екеуi де шексiз меншiксiз интеграл
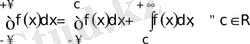 (4. 2)
(4. 2)
қарастыралады. Теңдiктiң оң жағындағы меншiксiз инетгралдардың екеуi де жинақты болса, онда бүкiл сандық ось бойынша алынған меншiксiз интеграл да жинақты. Қосылғыш меншiксiз инетгралдардың кемiнде бiреуi жанықсыз болса, онда (4. 2) - нің сол жағындағы меншiксiз интеграл да жинақсыз.
Сонымен, I-тектi меншiксiз интеграл дегенiмiз интегралдау шектерi
 - ке ұмтылғандағы анықталған инетгралдың шегi. Сондықтан оны есептеу үшiн Ньютон-Лейбниц формуласы қолданылады. Егер
- ке ұмтылғандағы анықталған инетгралдың шегi. Сондықтан оны есептеу үшiн Ньютон-Лейбниц формуласы қолданылады. Егер
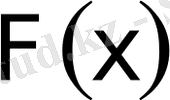 инетгралданушы функияның
инетгралданушы функияның
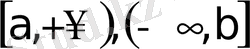 аралықтарындағы төркiн функциясы болса, онда:
аралықтарындағы төркiн функциясы болса, онда:
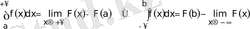 . (4. 3)
. (4. 3)
Ньютон-Лейбництiң жалпыланған формуласын әдеттегiше (3. 15) жаза беруге болады:
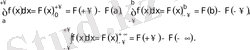
Тек
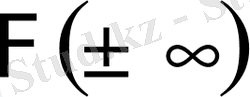 деп төркiн функцияның (4. 3) -тегі сәйкес
деп төркiн функцияның (4. 3) -тегі сәйкес
 -дағы шектерiн түсiну қажет.
-дағы шектерiн түсiну қажет.
Мысал:
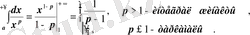
II-тектi меншiксiз интегралдар.
Функция шектелмеген нүкте (екiншi тектi үзiктiк нүктесi) функцияның ерекше нүктесi деп аталады. Интералдау кесiндiсiнiң
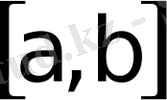 бастапқы
бастапқы
 , соңғы
, соңғы
 және кез келген iшкi
және кез келген iшкi
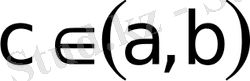 нүктелерi интегралданушы функцияның ерекше нүктелерi болып келген жағдайларды қарастыралық. Функция
нүктелерi интегралданушы функцияның ерекше нүктелерi болып келген жағдайларды қарастыралық. Функция
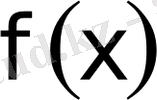 тек кесiндiнiң шеткi нүктелерiнiң бiрiнде ғана шектелмеген болса, онда жеткiлiктi аз
тек кесiндiнiң шеткi нүктелерiнiң бiрiнде ғана шектелмеген болса, онда жеткiлiктi аз

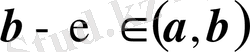 саны үшiн
саны үшiн
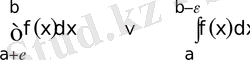 . 3. (4. 4)
. 3. (4. 4)
анықталған интегралы бар. Олардың шектерi
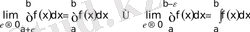 (4. 5)
(4. 5)
шектелмеген
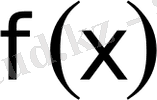 функциясынан алынған
(II-тектi) меншiксiз интеграл
деп аталады.
функциясынан алынған
(II-тектi) меншiксiз интеграл
деп аталады.
Егер
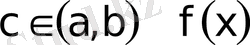 функциясының
функциясының
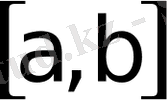 кесiндiдегi жалғыз ғана ерекше нүктесi болса, онда интегралдың аймақ бойынша аддитивтiк қасиетiн пайдалып,
кесiндiдегi жалғыз ғана ерекше нүктесi болса, онда интегралдың аймақ бойынша аддитивтiк қасиетiн пайдалып,
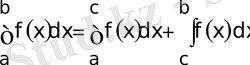 (4. 6)
(4. 6)
деп жаза аламыз. Теңдiктiң оң жағында II-тектi меншiксiз интегралдардың қаралған (4. 5) түрлерi тұр. Олардың жинақты-жинақсыздығы жайында тек I-тектi меншiксiз интегралдар (4. 1-4. 2) туралы айтылғандарды қайталауға болады.
Мысал:
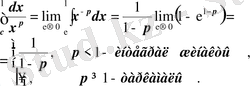
Қаралған мысалдарда
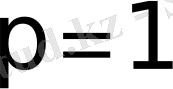 болса:
болса:
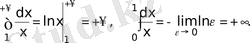
Тиiстi аралықта терiс емес функциядан алынған жинақты меншiксiз интегралдың геометриялық мағынасы бар. Мысалы, (4. 1) және (4. 5) интегралдарының бiрiншiлерi жинақты болса, олардың шамалары жоғарыдан
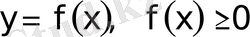 қисығымен шектелген шексiз, бiрақ, квадратталатын қисықсызықты трапециялардың (4
а), б) -сурет)
аудандарына тең. Интегралданушы функцияның интервалда саны шектi
қисығымен шектелген шексiз, бiрақ, квадратталатын қисықсызықты трапециялардың (4
а), б) -сурет)
аудандарына тең. Интегралданушы функцияның интервалда саны шектi
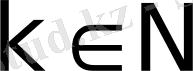 ерекше нүктелерi
ерекше нүктелерi
 бар, бiрақ оның төркiн функциясы
бар, бiрақ оның төркiн функциясы
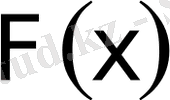 бүкiл
бүкiл
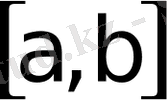 кесiндiсiнде үзiксiз болса, онда II-тектi меншiксiз интегралды есептеу үшiн Ньютон-Лейбниц формуласын (3. 15) түрiнде ерекше нүктелерге көңiл аудармай тұтас кесiндiге
кесiндiсiнде үзiксiз болса, онда II-тектi меншiксiз интегралды есептеу үшiн Ньютон-Лейбниц формуласын (3. 15) түрiнде ерекше нүктелерге көңiл аудармай тұтас кесiндiге
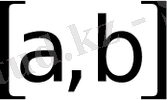 қолдана беруге болады.
қолдана беруге болады.
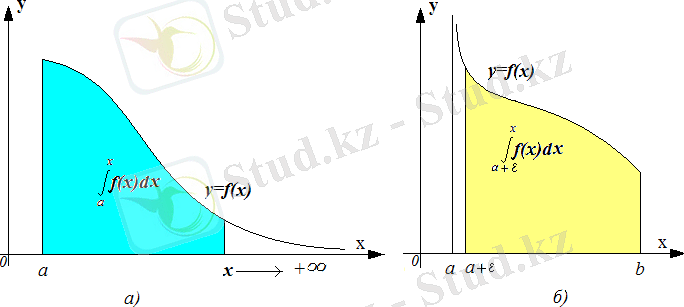 4-cурет
4-cурет
Практикалық сабақтарға нұсқау
1 Сабақ. Жиындар мен математикалық логика элементтері. Нақты сандар және олардың қасиеттері. Бірінің ішінде бірі кесінділер қағидасы. Жиындар. Жиындарға қолданылатын амалдар.
Есептерді шығару тәсілдері.
1 - есеп:
1/2 және 1/3 сандары
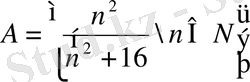 жиынның мүшесі бола ма?
жиынның мүшесі бола ма?
Шешуі:
А- жиынның мүшелері
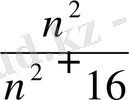 түріндегі бөлшектер болады, n - натурал сан.
түріндегі бөлшектер болады, n - натурал сан.
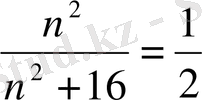 Теңдеуін шешіңіз
Теңдеуін шешіңіз
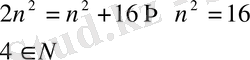 болады
болады
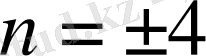
Сонда
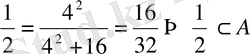
Енді
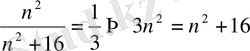
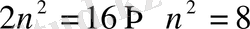
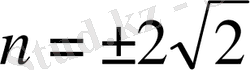
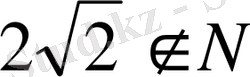 сондықтан
сондықтан
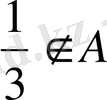 .
.
2 - есеп:
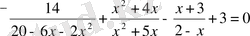 теңдеуінің шешіімдерінің жиынын табу қажет.
теңдеуінің шешіімдерінің жиынын табу қажет.
Шешуі: бөлшектерді ортақ бөлімге келтіріңіз, сонда
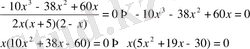
Шешімдері,

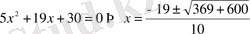
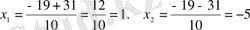
Бұл түбірлердің тек х=1, 2 мәнін теңдеуімізді қанағаттандырады, сонда А={1, 2}
3 - есеп:
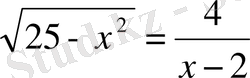 теңдеуін қанағаттандыратын айнымалының мәндерін табу қажет.
теңдеуін қанағаттандыратын айнымалының мәндерін табу қажет.
Шешуі:
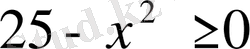 болған жағдайда мағынасы бар болады, яғни, Х∈[-5, 5]
болған жағдайда мағынасы бар болады, яғни, Х∈[-5, 5]
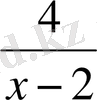 бөлшегін Х≠2 болғанда мағынасы болады. Х∈ (-∞, 2) ∪ (2; + ∞), [-5, 5] және (-∞; 2) ∪ (2, +∞ ) жиындар жолының бөлігі [-5, 2) ∪ (2, 5] жиыны болады.
бөлшегін Х≠2 болғанда мағынасы болады. Х∈ (-∞, 2) ∪ (2; + ∞), [-5, 5] және (-∞; 2) ∪ (2, +∞ ) жиындар жолының бөлігі [-5, 2) ∪ (2, 5] жиыны болады.
4 - есеп.
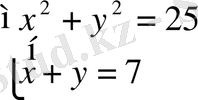 Теңдеулер жүйесіндегі шешімдер жиынын табу қажет.
Теңдеулер жүйесіндегі шешімдер жиынын табу қажет.
Шешуі:
Мұнда А жиыны
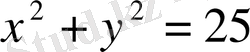 теңдеуін қанағаттандыратын қос сандар жиыны. Ал В-х+у=7 түзуінің бойында жататын нүктелер координаталарының жиыны. Сонда жүйенің шешімі осы екі жиынның қиылысуы болады
А∩В.
Бұл жағдайда графикпен көрсеткен қолайлы. Шеңбер мен түзу М және N нүктелерінде қиылысуы М (3, 4) N (4, 3) сонда
А∩В =
{(3. 4), (4. 3) }
теңдеуін қанағаттандыратын қос сандар жиыны. Ал В-х+у=7 түзуінің бойында жататын нүктелер координаталарының жиыны. Сонда жүйенің шешімі осы екі жиынның қиылысуы болады
А∩В.
Бұл жағдайда графикпен көрсеткен қолайлы. Шеңбер мен түзу М және N нүктелерінде қиылысуы М (3, 4) N (4, 3) сонда
А∩В =
{(3. 4), (4. 3) }
5 - есеп.
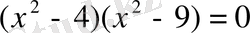 Теңдеуінің шешімдері жиындарын табу керек.
Теңдеуінің шешімдері жиындарын табу керек.
Шешуі: көбейтінді 0-ге тең болады, егер көбейткіштердің бірігуі 0-ге тең болса. Сонда А жиыны
 теңдеуінің шешімдер жиыны.
теңдеуінің шешімдер жиыны.
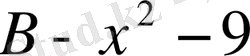 теңдеуінің шешімдер жиыны. А={-2. 2} B={-3. 3} Теңдеуінің шешімдер A∪B = {-3, 2, 2, 3} болады.
теңдеуінің шешімдер жиыны. А={-2. 2} B={-3. 3} Теңдеуінің шешімдер A∪B = {-3, 2, 2, 3} болады.
Есеп - 1: Аудиторияда 25 студент отыр делік. Оның 15 - і шахматпен шұғылданады, 20 - сы футболмен, ал 12 - сі шахмат және футболмен де айналысады. Біз футбол және шахматпен де айналыспайтын студенттер бар ма екенін анықтайық.
Шешуі: А - арқылы жиын берілсе U(А) -ның мүшелерінің санын белгілейміз. Шахмат және футболмен айналысатын студенттер саны 15+20=35 бірақ, бұл жерде шахмат және футболмен де айналысатын студенттер екі рет санаққа алынды. Сондықтан шын мәнінде аудиториядағы студенттер шахмат немесе футболмен айналысып, оны табу үшін 15+20=35 қосындысы екі рет санаққа алынған студенттерді шығарамыз. 15+20-12=23. Ал барлығы 25 болғандықтан 25 -23 =2 студент не шахматқа не футболға бармайды екен. Бұл есепті мына алгоритм шешуге болады. А- шахматшы, В- футболшы жиындар. Сонда
U(A∪B) =U(A) +U(B) -U(A∩B) (1)
U(A) =15 n(B) =20 U(A∩B) =10
U(A∪B) =15+20-10=23
7 - есеп. Институттың бір бөлімінде 6- ағылшын, 6- неміс, 7-француз, 4 - ағылшын және неміс, 3-неміс және француз, 2 - ағылшын және француз және бір үш тілді білетін кісілер жұмыс істейді. Бөлімде неше кісі бар: неше кісі осы үшеуінің тек бір тілін ғана біледі.
Шешуі: А-ағылшын тілін, В-неміс, С- француз тілін білетін кісілер жиындары болсын. Сонда
n(A) =6, n(B) =6, n(C) =7, n(A∩B) =4, n(B∩C) =3.
n(A∩C) =2, n(A∩B∩C) =1
n(A∩B∪C) =n(A) +n(B) +n(C) -n(A∩B) -n(A∩C) -n(B∩C) +n(A∩B∩C) =6+6+7-4-3-1+1=12.
Енді бір тілден көп білетін кісілер саны n(A∩C) +n(A∩B∩C) =4+3+1+1=9 болады. Онда осы үш тілдің тек біреуін ғана білетін кісі саны n(A∪B∪C) -n(A∩B) -n(B∩C) -n(A∩C) -n(A∩B∩C) =12-9=3. Барлығы 12 кісі және оның ішінде 3-і айтылған үш тілден тек біреуін ғана біледі.
Жаттығулар:
1. Сізге белгілі әскер қызметкерлер жиынын атаңыз.
2. Университет құрамының жиынын атаңыздар
3. А - сүт көрсеткішті жиын, В - құс жиыны, С - шыбын - шіркей жиыны.
а) А- жиынның; б) В - жиынның; в) С-жиынның суда өмір сүре алатын мүшелерін атаңыздар.
4. Жиынның 3- мүшесін атаңыздар:
а) 3-ке еселі және 5-ке бөлінбейтін
б) 3-ке еселі және тек 2-ге бөлінетін
в) 5 -ке еселі тек 25 -ке бөлінетін
г)
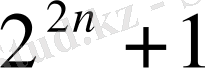 түрінің жай сан болатынын
түрінің жай сан болатынын
д) 2n + 1 түрінің құрамы сан болатынын
5. Егер А - ға бөлінетін сан жиыны болса, ода мына жазғандар дұрыс па?
1) 7€ А, 2) 10€ А, 3) 15€А;
А- жиынның мүшелерінің тізімін жаса.
6.
Егер А жиыны
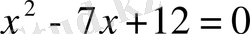 теңдеуінің шешімдер жиыны болса, онда мына жазғандар дұрыс па?
теңдеуінің шешімдер жиыны болса, онда мына жазғандар дұрыс па?
3€ А, -5€ А, 10¢А, 4¢А
А - жиынның мүшелер тізімін жаса.
7. А - барлық үшбұрыштың жиыны. 1 -сурет
а) Бұл жиын неше мүшеден тұрады.
б) Жиында қандай геометриялық фигуралар бар.
8. Ақырлы және ақырсыз жиындар болатын 3 мысал келтір.
9. Берілген қасиеттерді қанағаттандыратын жиын мүшелерін атаңыз.
а)
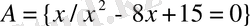 c)
c)
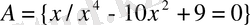
b) A = {x/-12 <x≤-56 x€N} d) A= {x/-1≤x≤8. 56 x€N}
10
.
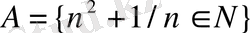
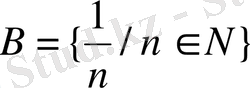
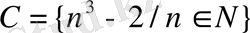
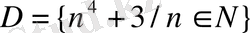 жиындар берілсе:
жиындар берілсе:
а) Әрқайсысынан 3 мүшесін тап.
б) 3, 4, 5, 13, 25 сандары мүше болатын жиынды тап.
в) берілген сандар мүше болмайтын жиынды тап.
11.
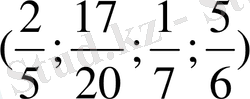 сандардың қайсысы
сандардың қайсысы
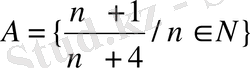
жиындарының мүшелері болады.
12. Б ерілген жиындардың заңдылығын табыңдар.
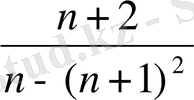
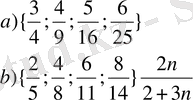
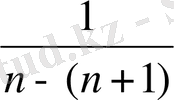
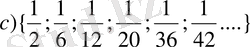
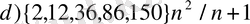
13. Берілген бүтін (жиынның) санды мүшелері жоқтығын дәлелдеңдер.
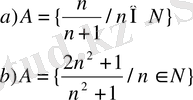
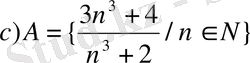
- Берілген жиындардың қайсысы бос болады.
а) Екі қарама - қарсы қабырғалары параллель болатын төртбұрыштар жиыны.
б) Бойы 1, 6 м биік адамдар жиыны.
в)
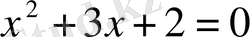 теңдеуін бүтін санды шешімдер жиыны.
теңдеуін бүтін санды шешімдер жиыны.
г) Координаттары натурал сандар болып
 Түзуінің бойында жататын нүктелер жиыны.
Түзуінің бойында жататын нүктелер жиыны.
- Теңдік орындалатын айнымалылардың мәндер жиыны тап.
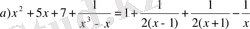
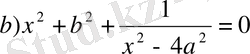
- Теңдеулер шешімінің жиынын тап.

- F(1, -2) нүктесінен және х = 2 түзуін бірдей арақашықтықта жобасын М(ху) нүктелер жиынның теңдеуін табыңдар.
- Шеңбердің теңдеуін жазыңдар, егер:
а) ортасы А(-1, 2) нүктесінде, ал радиусы 5-ке тең болса;
б) ортасы А(3, 1) нүктесінде және шеңбер В(7, 4) нүктесінен өтетін болса.
в) Шеңбер А(4, 6), В(-2, 2) нүктелерден өтеді және радиусы 5-ке тең.
г) Шеңбер АВС үшбұрышқа сырттай сызылған және координаталары А(9, 2), В(7, 6), С(0, -1) болса
д) Шеңбер АВС үшбұрышына іштей сызылған және координаталары А(2, 3), В(7, 4), С(5, 6) болса;
- Жазықтықтың М(х, у) нүктелер жиынын табыңдар, егер олар үшін:
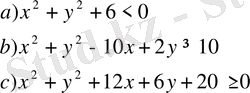
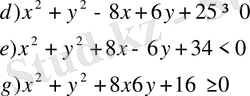
- Жазықтықтың М(х, у) нүктелер жиынын табыңдар, егер олар үшін:
- А - дұрыс көпбұрыштар жиынын В - барлық үшбұрыштар жиыныA∩Bне болатынын табыңдар.
- A∩Bтабыңдар, егер:
а) А = [0, 4], В = [ 1, 5],
б) А = [0, 2], В = [ 3, 7]
в) А - жұп натурал сандар жиынын, В - 3 бөлінетін сандар жиынын
г) А ={x/x =2m+1, m∈N}
д) B = {x/x =3n +2, n∈N }
- Теңдеулер жүйесінің шешімін табыңдар.
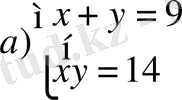
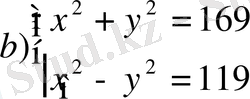
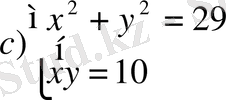
- А-4к+1 түріндегі бүтін сандар жиыны В-4к+3 сандар жиыны. A∪B -жиынын табыңдар.
- А = {2n \, n∈N } B = {2n +1/ n∈N } болғандаA∪B -жиынын табыңдар.
- Теңдеулердің сол жағын көбейткіштерге жіктеп, шешіңдер, жиынын табыңдар.
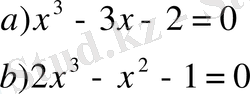
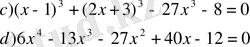
- Теңдеулер жүйесінің шешімін табыңдар:
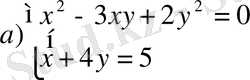
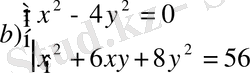
- Жиындарды анықтаңдар:
а) СØ, б) СU в) С А А С А А
29. А= [ 1, 4], В=[2, 6] болса А/В және В/А - ны табыңдар.
30. А= {х/х = 2m-1, m - бүтін сан }
B= {x/x = 4n+1, n - бүтін сан}
А/В-ны табыңдар.
31. A=[1. 6], B=[2. 7], C=[-1. 3] 6 D=[2. 5] болса, табу қажет:
а) A ∪B∪C∪D г) (A∪B) ∩(C∪D)
б) A∩B∩C∩D д) ((A∪B) ∩C) ∪D
в) (A∩B) ∪(C∩D)
32. А- ағылшын тілін оқитын топ жиыны. В - неміс тілін, С - француз тілін оқитын жиындар төмендегі жиындар сипатталады:
а) (A∩B) ∩C, б) A∪(B∩C), в) (A∪B) ∩(B∪C)
33. Эйлер - Венн диаграммасы арқылы
a) С(А∪В) =CA∩CB 6) C(A∩B) =CA∪CB) болатыны көрсетіңіз.
34 . Жиын алгебрасының ережесі бойынша ((А∪С) ∩(А∪В) ) /((А∪В/С) ) ∩А.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz