Екіөлшемді дискретті кездейсоқ шамалар

Жоспар
Кіріспе

Кіріспе
1 Екіөлшемді дискретті кездейсоқ шамалар жәке олардыц үлестіру заңдары
2 Кездейсок, шама функциясы, кездейсоқ шамаларға қолданатын операциялар
3 Екі өлшемді кездейсоқ шамалардың шартты үлестіру
4 Екіөлшемді кездейсоқ шамалардың үлестіру функциялары және үлестіру тығыздығы
5 Екі кездейсоқ шама жүйесінің үлестіру заңы бойынша оны құраушы кездейсоқ шамалардың үлестіру заңдарын анықтау

Осыған дейін айтылған кездейсоқ шамаларды бірөлшемді кездейсоқ шамалар деп те айтады. Сондай-ақ екі өлшемді, үш өлшемді, жалпы, көпелшемді (бірнеше өлшемді) кездейсоқ шамаларды да қарастыруға болады. Бірөлшемді кездейсоқ шамаларды қарастырғанда, олар әр түрлі сандық мәндерді қабылдайтынын, геометриялық кескіні түзу бойындағы нүктелер болатынын байқадық. Осыған орай жазықтықтағы нүктелерді кес-кіндейтін кездейсоқ шамаларды екіөлшемді, ал кеңістіктегі нүктелерді кескіндейтін кездейсоқ шамаларды үш-өлшемді деуге болады. Қездейсоқ шаманың өлшемі үш-тен көп болса, оны геометриялық кескіндеуге болмайтынын ескертеміз.
Сонымен, Х1, X2, ... ,Хп кездейсоқ шамалары берілсе, оны n-өлшемді кездейсоқ шама (фактор) дейміз. Бірөлшемді кездейсоқ шама сияқты көпөлшемді кездейсоқ шамалар да дискретті және үздіксіз болады. Қөрнекілік жағын көздеп негізінде екіөлшемді кездейсоқ шамаларды қарастырамыз. Олар үшін айтылғандарды әрі қарай кепөлшемді кездейсоқ шамаларға тарату қиынға сокпайтынын ескертеміз. Алдымен дискретті кездейсоқ шамалар мен олардың үлестіру заңдарын қарастырудан бастайық.

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 15 бет
Таңдаулыға:

Кіріспе

Осыған дейін айтылған кездейсоқ шамаларды бірөлшемді кездейсоқ шамалар
деп те айтады. Сондай-ақ екі өлшемді, үш өлшемді, жалпы, көпелшемді
(бірнеше өлшемді) кездейсоқ шамаларды да қарастыруға болады. Бірөлшемді
кездейсоқ шамаларды қарастырғанда, олар әр түрлі сандық мәндерді
қабылдайтынын, геометриялық кескіні түзу бойындағы нүктелер болатынын
байқадық. Осыған орай жазықтықтағы нүктелерді кес-кіндейтін кездейсоқ
шамаларды екіөлшемді, ал кеңістіктегі нүктелерді кескіндейтін кездейсоқ
шамаларды үш-өлшемді деуге болады. Қездейсоқ шаманың өлшемі үш-тен көп
болса, оны геометриялық кескіндеуге болмайтынын ескертеміз.
Сонымен, Х1, X2, ... ,Хп кездейсоқ шамалары берілсе, оны n-өлшемді
кездейсоқ шама (фактор) дейміз. Бірөлшемді кездейсоқ шама сияқты көпөлшемді
кездейсоқ шамалар да дискретті және үздіксіз болады. Қөрнекілік жағын
көздеп негізінде екіөлшемді кездейсоқ шамаларды қарастырамыз. Олар үшін
айтылғандарды әрі қарай кепөлшемді кездейсоқ шамаларға тарату қиынға
сокпайтынын ескертеміз. Алдымен дискретті кездейсоқ шамалар мен олардың
үлестіру заңдарын қарастырудан бастайық.

Екіөлшемді дискретті кездейсоқ шамалар жәке олардыц үлестіру заңдары

Біз екіөлшемді кездейсоқ шамалар мен олардын үлестіру заңдарын
қарастыруды мысалдан бастайық.
1 - мысал. Туған жас нәрестенің ұл болуын 1 цифрымен, қыз болуын 0
цифрымен белгілейік. Сонда егіз сәбилер (X, У) екіөлшемді кездейсоқ шама
болады. Мұның қабылдайтын мәндері (1,1), (1.0), (0,1), (0,0).
Осы айтылғандар дәлелді болу үшін тікбұрышты координаттар ұғымын
енгізейік. Сонда жазықтықтағы әрбір нүктені екіөлшемді кездейсоқ шама (Xі,
Ү) деп координаттар жүйесіндей (х1г, уі) (j =1, 2, ...) сандары парымен
өрнектелген координаттарды сол кездейсоқ шама (X, Ү) мәндері деп
қарастыруымызға болады. Бұлар дискретті кездейсоқ шама болғандықтан,
бірөлшемді дискретті кездейсоқ шама сияқты, екіөлшемді дискретті кездейсоқ
шама мәндері шекті де, саналымды шексіз де болуы мүмкіндігін ескертеміз.
Ал әрбір координаттың өзін алсақ, ол бұрыннан мәлім бірөлшемді
кездейсоқ шама. Мұндағы х1 х2, ... , хп және у1, у2, ... , у„ ... мәндері —
сол X және Ү бірөлшемді кездейсоқ шамаларының мәндері. Олай болса,
екіөлшемді кездейсоқ шаманы екі бірөлшемді кездейсоқ шамалар жүйесі деп те
айта аламыз. Сондай-ақ бірөлшемді дискретті кездейсоқ шаманың үлестіру
заңына берілген анықтама сияқты екіөлшемді дискретті кездейсоқ шаманың
үлестіру заңы да сол шаманың хі, уі - мәндері мен оларға сәйкес келетін
ықтималдықтар жиыны арқылы анықталады. Бұл жайт төмендегі 1 және 2-
таблицалардан айқын байқалады. Бұл таблицалардың жолдарында кездейсоқ шама
абсциссалар Х-тің қабылдайтын мәндері, ал бағаналарында кездейсоқ шама
ординаталар У-тің қабылдайтын мәндері көрсетілген. Екіөлшемді кездейсоқ
шама (X, У)-тің мәнін қабылдауын X кездейсоқ шамасының хі мәні мен У
кездейсоқ шамасының уі мәнінің бірден пайда болу оқиғасы деп ұғамыз. Бұл
күрделі оқиға (X =хі, Ү=уі) ықтималдығын ріj деп белгілесек, онда
Ріj=Р(Х = Хі, Ү=Уі) = Р(Хі, у}), і, =1, 2, ...
келіп шығады.
Бағана мен жолдың қиылысуында осы ріj ыктималдығының мәндері
келтірілген. Бұлардың қосындысы 1-ге тең, яғни

P{Хі, Уі)=1, рij=1.
i=1 j=1 i=1 j=1

1-таблица
Y
X y1 y2
X1 P(x1, y1) P(x1, y2) . P(x1)
X2 P(x2, y1) P(x2, y2) . . P(x2)
. . . .
. .
. .
.
P( y1) P( y2) . 1.00
. .

Түсінуге жеңіл болуы үшін (X, Ү) қабылдайтын мәндерді шекті деп
ұйғарамыз, ягни (хi, уj) нүктелеріндегі і индексі 1-ден n-ға дейін,
индексі 1-ден m-ға дейін өзгереді дейміз. Сонда 1-таблицаны 2-таблица
түрінде жазуымызға болады.
2 - т а б л и ц а

Y y1 y2 . . . yj . . .ym Pj=P(x1)
X
Pj=Pyj P(y1) P(y2) . . P(yj) . . P(ym) 1.00
. .

1 және 2-таблицалар (X, Ү) дискретті кездейсоқ шамасының үлестіру заңы
делінеді. Үлестіру заңының графиктік түрде және формула түрінде де
берілетінін ескертеміз. (X, Ү) шамасының үлестіруі бойынша X және У
кездейсоқ шамаларының әрқайсысына тең үлестіру заңын да алуға болады.
Шынында да Х=Хі оқиғасы (Х= y1Ү= y1), (Х=Хі, Ү=у2), (Х = х = Хі, Ү =Ут)
оқиғалары қосындысына тең, өйткені Х=Хі мәнін қабылдауы У-тің қандай
мәндерді кабылдауына байланыссыз. Сонымен қатар бұл оқиғалар үйлесімсіз,
олай болса, қосу теоремасы бойынша Рi=Р(хi=Р(х=Хi) = Р (Хi,у1) +
іР(хi у2)+... + Р(Хi, ут) немесе
m m
Рі = Р (хi, yi) = =pіj
j=1 j=1
Бұл ықтималдықтар таблицаның соңғы бағанасына жа-зылған. Осы сияқты
n n
Рі = Р(yі) =Р(Y = yi) = Р (хi. yi)=р ji
ықтималдықтары таблицаның соңғы жолына жазылған. Бұл айтылғаннан екіөлшемді
дискретті кездейсоқ шаманың үлестіру заңын білсек, онда оның құрамындағы
әрбір кездейсоқ шаманың үлестіру заңын да шығаруға болатынын байқаймыз.
Бұдан бірөлшемді үлестіруден соңғы формулалар бойынша екіелшемді кездейсоқ
ша-маның үлестіруін аламыз деуге болмайды. Оны алу үшін X, Ү кездейсоқ
шамаларының тәуелсіз болуы сияқты қосымша информация қажет болады.
м ы с а л. Нысана үш зонадан тұрады. Атқыш бір рет нысананы дәлдеп оқ
атады. Оқ бірінші зонаға тисе 5 ұпай алады, екіншіге тисе 4 ұпай, үшіншіге
тисе 1 ұпай алады. Бұл зоналарға тию ықтималдықтары сәйкес 0,1; 0,3; 0,5
сандарына тең. Атқыш екінші рет жылжып бара жатқан затты дәлдеп оқ атқан.
Бұл жолы атқыш ныса-наға тисе 4 ұпай алады, ал тигізе алмаса 2 ұпай жоғал-
тады, нысанаға дәл тию ықтималдығы 0,4-ке тең. Үлесті-ру таблицасын (заңын)
анықтау керек.
Ш е ш у і. Ату нәтижесі екіөлшемі кездейсоқ (X, Ү) шамасымен
сипатталады. Мұнда X бірінші рет атылған-да алынған ұпайлар саны да, V
екінші рет атқанда алыи-ған ұпайлар саны. Бұл кездейсоқ шаманың үлестірілу
заңы төменде келтірілген 3-таблица болады. Жолдар мен баганалар қиылысуында
Р(xi yi) ықтималдықтарының мендері жазылған. Осы P(хji, уj) мәндерін
анықтайық. Есептің шарты бойынша
р(Хі) = Р(Х = 5) =0,1; Р(х2)=Р(Х= 4) =0,3; P(х3) = Р(Х=1) =0,5; Р(X=4)
= Р(Х = 0) = 1 - [Р(А = 5) +Р)Х =
=4)+P(X=1)]=0.1 Сондан-ақ Р(у2) =Р(Y = 2) =Р(Ү =4) =0,4.
Р(у2) =Р(Y = -2) =1-Р(Ү =4) =0,6.

Ықтималдықтардың бұл мондері 3-таблицанын, ең сон.ғы бағанасындағы
Р(хj) мәндері мен ең соңғы жо-лындағы Рji(У) мәндері болмақ. Ал
клеткадағы Рji = Р(Х = xi, Ү = уj) мәндерін анықтау үшін Х=хj және Ү
=yі оқиғаларының бір-біріне тәуелсіздігін пайдаланамыз. Сонда формула
бойынша Р (хi уj) = Р (хі)Р (yj) болады. Енді Хі -дің әрбір 5, 4, 1,0
мэндеріне уj-дің сәйкес 4,-2 мәндері бойынша Р(хi у-j
ықтималдығын есептейміз. Сонда хi = 5, уj =4 болғанда P(xj уj) = Р(Х=5,
Ү=4) = Р (x= 5)Р(Ү = 4)=0,1*0,4=0,04. Осы сияқты басқаларын есептейміз,
сонда
Р(х1 у2)= 0,1 *0,6 = 0,06, Р(х2, ух) =0,3*0,4 = 0,12.
Р(х2, y2) =0,3*0,6 = 0,18, Р(x3, у1) =0,5*0,4 = 0,2,
Р(x3, у2) =0,5*0,6 = 0,3, Р(х4, ух) =0,1 *0,4 = 0,04,
Р(x4, у2) =0,1*0,6 = 0,06.
Бұларды 2-таблицаға қойып іздеген үлестіру заңып 3-таблица түрінде аламыз.
3 - т а б л и ц а
Y 4 -2 P(x)
Х
5 0.04 0.06 0.10
4 0.12 0.18 0.30
1 0.20 0.30 0.50
0 0.04 0.06 0.10
P(yj) 0.40 0.60 1.00

Кездейсок, шама функциясы, кездейсоқ шамаларға қолданатын операциялар

Кездейсоқ шамаларға қолданатын операциялардың сандарға қолданатын
операциялардан айырмашылығы бар. Өткен параграфта кездейсоқ шаманың берілуі
оның үлестіру заңымен анықталатынын айттық. Енді кездейсоқ шамалар
ықтималдықтарының үлестіру заңдары арасындағы байланысты көрсетейік. Ол
үшін кездейсоқ шама (аргумент) функциясы ұғымын енгізейік.
Алдымен дискретті кездейсоқ шама функциясын қарастырайық және мұны
кездейсоқ шамаларға қолданатын операцияларға пайдаланайық. 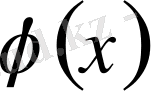кездейсоқ
шама Х-тің барлық мүмкін х мәндері жиынында анықталған функциясы болсын.
Егер X кездейсоқ шамасы х мәнін қабылдағанда Ү кездейсоқ шамасы у =
(х) мәнін қабылдаса, онда Y-ті Х-тің функциясы дейміз, сөйтіп
Ү=(Х) түрінде жазамыз. Әрине 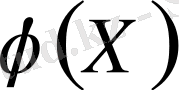әр түрлі формада берілуі мүмкін.
Дискретті кездейсоқ X шамасы 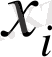мәнін 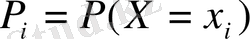ықтималдықпен қабылдаса
(таблицаны қара), онда 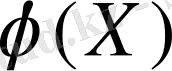функциясының мүмкін мәндері 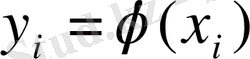болар еді,
бірақ бұларға сәйкес ықтималдықтарды анықтау керек. Х-тің үлестірілу
таблицасы жалпы
4-таблица
x x2 ... xn ...
Pi P1 P2 ... pn ...

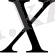
түрінде жазылады, мұнда 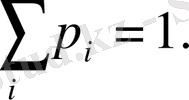Түсінуге қолайлы болу үшін біз алғашқы
мәндерімен шектелеміз.
Ү-тің ықтималдықтарын анықтауда мынадай дербес жағдайлар кездесуі
мүмкін, солардың анықтамасын келтірейік.
1.Кездейсоқ шама X пен тұрақты k-ның көбейтіндісінен шыққан жаңа
кездейсоқ шама Ү=кХ мәндері сол кездейсоқ шама X мәндерін к еселегенге тең
де ықтималдықтары Х-тің ықтималдығындай болады
2. Х-тің қабылдайтын әрбір хі (і=1, 2, ...) мәндеріне сәйкес Ү-тің
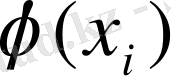мәндері әр түрлі болса да оларға (X пен Ү-ке) сәйкес ықтималдықтар
бірдей болады. Өйткені Х=хі мәнін қабылдағанда ғана Ү =уі=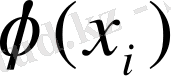мәнін
қабылдайды. Бұл жағдайда X пен Ү шамаларының үлестірілу таблицаларындағы
айырмашылық тек бұлардың қабылдайтын мәндерінде ғана болады да, сәйкес ықти-
малдықтары бірдей болады

5-таблица
kx1 ...
...

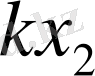
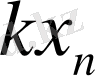
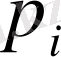
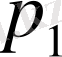
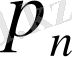
6-таблица
...
...

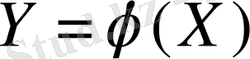
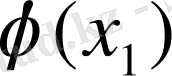
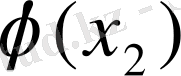
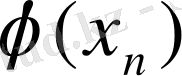
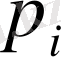
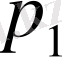
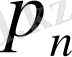
3. Х-тің қабылдайтын әрбір хі мәндеріне сәйкес келетін
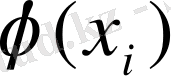мәндерінің ішінде бір-біріне тені болса, онда олардың біреуі ғана жазылып
сәйкес ықтималдықтарын қосу теоремасы бойынша қосылып жазылады.
... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.