Математикалық индукция әдісі: принциптері, дәлелдері және қолданылуы


Қазақстан Республикасы білім және ғылым министрлігі.
Қ. А. Яссауи атындағы Халықаралық Қазақ-түрік университеті.
Математика кафедрасы.
Тақырыбы: Математикалық индукция әдісі және оның
қолдануы
ТҮРКІСТАН-2008ж
Мазмұны:
Кіріспе . . . 3
I тарау Индукция ұғымы . . . 4
1. 1 Математикалық индукция әдісінің түсінігі . . . 4
1. 2 Ньютон биномын дәлелдеу . . . 5
1. 3 Индукция әдісін сандардың бөліну есептерінде қолдану . . . 6
II тарау Индукция тәсілі . . . 7
- Тепе- теңдіктерді дәлелдеу . . . 7
- Теңсіздіктерді дәлелдеу . . . 12
- Математикалық индукция әдісін басқа есептерде қолдану . . . 15
2. 4 Индукция әдісін басқа дәлелдеу жолдармен салыстыру . . . 18
Қорытынды . . . 21
Пайдаланылған әдебиеттер . . . 22
Кіріспе.
Бұл курстық жұмыста алгебра пәні бойынша « Математикалық индукция » тақырыбы қарастырылады . Курстық жұмыстың негізгі мақсаты берілген тақырыпты кең көлемде ұғыну және соған байланысты материалдарды үйрену болып табылады .
Индукцияның қазақша баламасы қорытындылау деген сөзбен тең . Яғни жалқыдан жалпыға өту. Мысалы біз күн сайын күннің шығыстан шығатынын көреміз. Сол себепті сенімді түрде күннің шығыстан шығатынын айтуға болады. Бұл қорытындыны біз ешқандай болжамдарға сүйеніп айтпаймыз, тек күннің қозғалысынан білеміз. Дегенмен бұл индуктивтік қорытынды біз жасаған бақылаумен сәйкес келеді. Бақылаудың тиімді жолы да, тиімсіз жолдары да бар, міне осы жағдайларда индукция әдісін пайдалану тиімді жолы көрсетіледі.
Курстық жұмыс екі тараудан тұрады . I тарауда математикалық индукция ұғымын еңгіземіз . Жиі кездесетін Ньютон Биномын математикалық индукция әдісімен дәлелдеп көрсетеміз . Сонымен қатар
кейбір сандардың бөлінуін математикалық индукция әдісі бойынша дәлелдейміз . II тарауда бұл әдісті тепе - теңдіктерді және теңсіздіктерді дәлелдеуде қолданамыз . Сондай-ақ бұл әдіс қандай жағдайларда қолдануға болады немесе қолдануға тиімсіз жағдайларында көрсетеміз . Сонымен қатар тәжірибелер жүргізетін ғылымдар үшін маңызы көп екенін көрсетеміз . Соңында курстық жұмысты қорытындылаймыз .
I тарау Индукция ұғымы
1. 1 Математикалық индукция әдісінің ережесі.
Математикалық индукция әдісі теоремаларды, тепе- теңдіктерді, теңсіздіктерді дәлелдегенде, сандардың бөлінетіндігін анықтағанда және әртүрлі есептер шығарғанда кеңінен қолданылады. Математикалық индукция принципін төмендегі аксиомамен тұжырымдауға болады.
Натурал n айнымалыға тәуелді А(n) тұжырым сол айнымалының барлық мәндері үшін дұрыс болады, егер төмендегі екі шарт орындалса.
1. n=1 болғанда A(n) тұжырым дұрыс болса.
2. n=k үшін /мұндағы k- кез-келген натурал сан/ A(n) тұжырымды дұрыс деп жорығанда, ол тұжырымның n=k+1 үшін де дұрыс екендігі шығатын болса.
Осы айтылған принципті математика принципі деп атайды. Теорема тікелей математикалық индукцияның аксиомасына байланысты дәлелденеді. Индукция аксиомасы: егер А
 N және 1) 1
N және 1) 1
 А, 2) n
А, 2) n
 A шартынан n+1
A шартынан n+1
 A болса, онда А=N.
A болса, онда А=N.
Сонымен, егер де р(n) тұжырымын барлық n натурал сандары үшін дұрыстығын тексергіміз келсе, онда: біріншіден осы тұжырымның n=1 болғандағы ақиқаттығын; екіншіден, осы тұжырымның n=k үшін дұрыс деген болжаудан, оның келесі n=k+1 саны үшін де дұрыс болатынын тексеруіміз керек. Сонда осы шарттар орындалғанда р(n) тұжырымы, математикалық индукция принципі бойынша, барлық натурал сандары үшін дұрыс болады.
1. 2. Ньютон биномын дәлелдеу.
Математикалық индукция әдісімен математикалық анлизде жиі қолданылатын Ньютон биномы деп аталатын формуланы дәлелдейік.
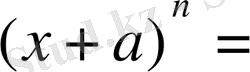
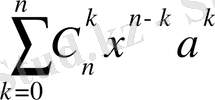 =
=
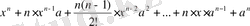
Мұндағы
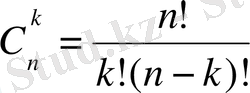 .
.
1. n=1 болса, онда x+a=x+a теңдігінің дұрыстығы шығады.
2. Ньютон биномы n үшін орынды деп жорып, оның n+1 үшін де орындалатынын дәлелдейік.
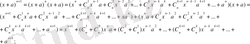
Енді мынаны есептейік:
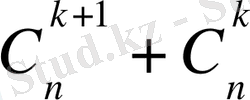 . Сонда,
. Сонда,
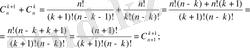
болады, яғни
 Бұл n+1 үшін Ньютон биномы. Қортындыда, барлық натурал n үшін Ньютон биномы орындалады.
Бұл n+1 үшін Ньютон биномы. Қортындыда, барлық натурал n үшін Ньютон биномы орындалады.
1. 3. Индукция әдісін сандардың бөліну есептерінде қолдану.
Мысал 1. Егер n - натурал сан болса, онда n²-n саны жұп екенін дәлелдеу керек.
Шешімі:
1. n=1 болса: 1-1=0 жұп сан болады.
2. n=k үшін дұрыс деп аламыз және k²-k=2m. /мұндағы m -натурал сан/ Енді n=k+1 үшін дұрыс екенін дәлелдейміз: (k+1) ²-(k+1) =k²-
-k+2k=2m+2k=2p болады, яғни n=k+1 үшін де дұрыс екенін көреміз. Сонымен есеп дәлелденді. Енді n²-n саны n натурал сандар үшін әрқашан жұп сан болады деп қорықпай айта аламыз.
Мысал 2.
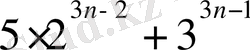
санның 19 ға қалдықсыз бөлінетіндігін дәлелдейік. n - натурал сан.
Шешімі:
Бұл есепті математикалық түрде жазайық:
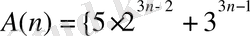 саны 19-ға еселік, n натурал сан
саны 19-ға еселік, n натурал сан
 орындалатындығын көрсетейік.
орындалатындығын көрсетейік.
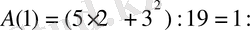
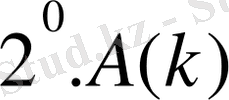 тұжырым орындалсын, яғни
тұжырым орындалсын, яғни
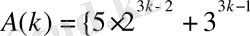 саны 19 ға еселік }, енді A(k+1) 19 ға еселік екендігін дәлелдейік. Шынында,
саны 19 ға еселік }, енді A(k+1) 19 ға еселік екендігін дәлелдейік. Шынында,
 Бұдан жоруымыз бойынша A(k) саны 19 ға еселік, демек бірінші жақшадағы өрнек 19 ға бөлінеді, ал екінші қосылғыштың 19 ға еселік екендігі көрініп тұр. Сондықтан A(k+1) дұрыс. Олай болса кезкелген n натурал сан үшін A(n) орындалады.
Бұдан жоруымыз бойынша A(k) саны 19 ға еселік, демек бірінші жақшадағы өрнек 19 ға бөлінеді, ал екінші қосылғыштың 19 ға еселік екендігі көрініп тұр. Сондықтан A(k+1) дұрыс. Олай болса кезкелген n натурал сан үшін A(n) орындалады.
II тарау Индукция тәсілі
2. 1. Тепе- теңдіктерді дәлелдеу .
Мысал 1. Мына формуланы дәлелдейік:
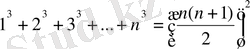 , n натурал сан үшін.
, n натурал сан үшін.
Шешімі:
n=1 үшін тексерейік:
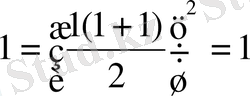 . Енді
. Енді
n=k үшін дұрыс деп ұйғарсақ
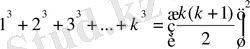 ; Бұдан n=k+1 үшін дұрыс екенін дәлелдейміз:
; Бұдан n=k+1 үшін дұрыс екенін дәлелдейміз:
 Сонымен n=k+1 үшін
Сонымен n=k+1 үшін
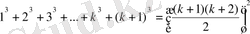 тепе- теңдігін дәлелдедік. Яғни индукция әдісінің шарттарын толығымен қанағаттандырып тұр. Бұдан формула дұрыстығы шығады.
тепе- теңдігін дәлелдедік. Яғни индукция әдісінің шарттарын толығымен қанағаттандырып тұр. Бұдан формула дұрыстығы шығады.
Мысал 2.
n натурал сандар тізбегінің қосындысы
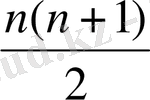 санына тең екендігін дәлелдеңіз.
санына тең екендігін дәлелдеңіз.
Шешімі.
n=1 үшін зерттесек.
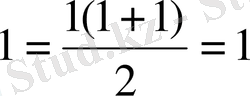 ал бұл теңдікті қанағаттандырады.
ал бұл теңдікті қанағаттандырады.
Тексеруді жалғастырсақ, n=k үшін дұрыс деп алып: 1+2+3+ . . . +k=
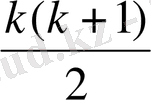 .
.
n=k+1 үшін дұрыстығын дәлелдейміз:
1+2+3+ . . . +k+(k+1) =
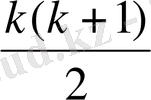 +(k+1) =
+(k+1) =
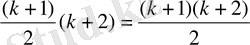 ;
;
Шынында да n=k+1 үшін дұрыс, онда n натурал саны үшін де теңдік орындалады.
Мысал 3.
n натурал сандар тізбегінің квадраттарының қосындысы
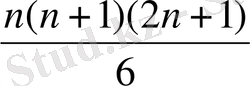 санына тең екендігін дәлелдейміз.
санына тең екендігін дәлелдейміз.
Шешімі:
Бірінші формуланы жазып алайық:
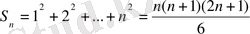 ;
;
1) . n=1 үшін:
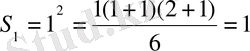 ; Енді екінші адымға өтеміз. 2) . Ол n=k үшін дұрыс деп ұйғаруымыздан шығады.
; Енді екінші адымға өтеміз. 2) . Ол n=k үшін дұрыс деп ұйғаруымыздан шығады.
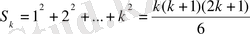 . Ол үшін n=k+1 үшін тексерсек болғаны:
. Ол үшін n=k+1 үшін тексерсек болғаны:

Яғни, n=k+1 үшін дұрыс болғандықтан n кезкелген натурал сандары үшін де теңдік дұрыс орындалады. Сонымен теңдік дәлелденді.
Мысал 4.
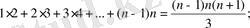 (1) .
(1) .
Теңдігінің дұрыстығын дәлелдейік.
Шешімі:
(1) - өрнекті
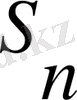 деп белгілеп алайық. 1) . Сонымен n=2 үшін тексерейік:
деп белгілеп алайық. 1) . Сонымен n=2 үшін тексерейік:
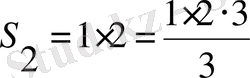 ;
;
2) . Енді n=k үшін
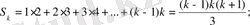 (2) .
(2) .
теңдігін дұрыс деп, n=k+1 үшін
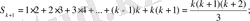 (3) .
(3) .
теңдігін дәлелдейік. (3) - өрнекті дәлелдеу үшін (2) - өрнекті пайдаланамыз:
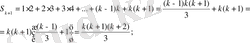
Шыныменде көріп отырғандай (3) - өрнекті дәлелдедік. Сонымен теңдік n натуралдар сандар үшін дұрыс орындалады.
Мысал 5.
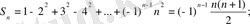
теңдігін дәлелдейік.
шешімі:
Алдымен n=1 үшін тексерейік. Айта кететін жайт бірінші қадамды n=1 үшін деп бастау шартты емес n=2, n=3, … сандары үшін де болады. Тек тексеруге қолайлы және оңай сан алған тиімдірек.
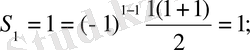 Бірінші қадамымыз дұрыс. Келесі қадамға өтсек.
Бірінші қадамымыз дұрыс. Келесі қадамға өтсек.
n=k үшін жорамалымыз дұрыс деп n=k+1 үшін тексерейік және
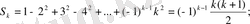
формуласын пайдаланып
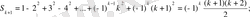
формуласының дұрыстығын дәлелдесек болғаны. Шынында да
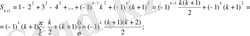
теңдігі орындалады. Ал бұл жорамалымыз шындыққа жанасады.
Сонымен кезкелген n натурал сандар үшін
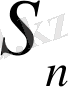 сандар қосындысының формуласы дұрыс екенін дәлелдедік.
сандар қосындысының формуласы дұрыс екенін дәлелдедік.
Мысал 6. Бұл формула комплекіс сандардың дәрежесін есептегенде көп қолданылады. Ал сол формуланың дұрыстығын индукциялық әдіспен дәлелдеп көрейік.
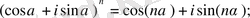 (1) .
(1) .
Дәлелдеу.
1) . n=2 үшін
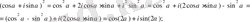
яғни (1) - өрнек n=2 үшін дұрыс екенін дәлелдедік.
2) . n=k үшін дұрыс деп:
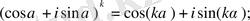 (2) .
(2) .
n=k+1 үшін
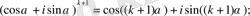 (3) .
(3) .
Сонымен (2) - өрнектің екі жағында
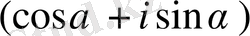 -ға көбейтсек:
-ға көбейтсек:
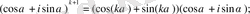 (4) .
(4) .
теңдігі шығады. Енді оң жағының жақшасын көбейтіп ашып ықшамдап жазатын болсақ:
 шығады. Сонымен (3) - өрнектің дұрыс екенін дәлелдедік. Ал бұл дегеніміз (1) - өрнек n- натурал сандар үшін дұрыс болады деген сөз. Теңдік дәлелденді.
шығады. Сонымен (3) - өрнектің дұрыс екенін дәлелдедік. Ал бұл дегеніміз (1) - өрнек n- натурал сандар үшін дұрыс болады деген сөз. Теңдік дәлелденді.
Сонымен қатар индукция әдісін тригонометриялық есептерде қолданып көрейік.
Мысал 7.
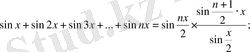 (1) .
(1) .
Теңдігін дәлелдейік.
Шешімі:
1) . n=1 болса
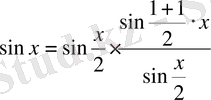

 болады.
болады.
2) . n=k үшін
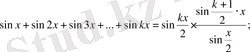 (2) .
(2) .
теңдігін дұрыс деп, n=k+1 үшін
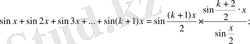 (3) .
(3) .
Теңдігінің дұрыстығын дәлелдейміз. Бұл (3) - теңдікті (2) - өрнектегі теңдікті пайдаланып дәлелдейміз. Олай болса (2) - өрнектің екі жағына
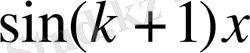
санына қосамыз. Сонда:
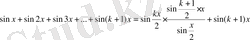
болады. Енді соңғы теңдікті ықшамдасақ:
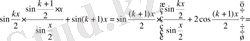

Сонымен (3) - өрнектегі теңсіздік дәлелденді. Бұл дегеніміз n натурал сандар үшін индукця әдісі бойынша (1) - өрнектегі теңдігі де дәлелденді дегеніміз.
2. 2. Теңсіздіктерді дәлелдеу.
Индукция әдісін теңсіздіктерді дәлелдеу тұрғысынан да қолдануға болады.
Әрине теңсіздіктерді басқа жолмен дәлелдеуге болады, бірақ индукция әдісі тиімді және қолайлы. Енді теңсіздіктерді дәлелдеп көрейік.
Мысал 1.
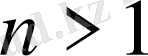 шартын қанағаттандыратын
шартын қанағаттандыратын
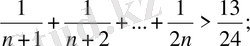
теңсіздігін дәлелдейік.
Шешімі.
Теңсіздіктің сол жағын
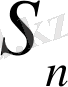 деп белгілеп алайық.
деп белгілеп алайық.
1) . n=2 болғанда:
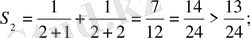 орындалады.
орындалады.
2) . n=k үшін,
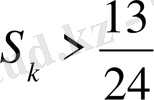 теңсіздігін дұрыс деп n=k+1 үшін
теңсіздігін дұрыс деп n=k+1 үшін
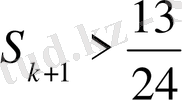 теңсіздігін дәлелдейік. Олай болса:
теңсіздігін дәлелдейік. Олай болса:
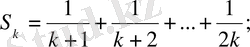
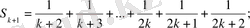
Екеуінің алындысын қарастырсақ:
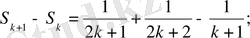 және де
және де
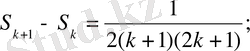
Кезкелген k натурал сандар үшін
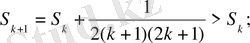
Ал бұл дегеніміз
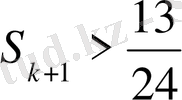 теңсіздігінің дұрыс екенін көрсетеді.
теңсіздігінің дұрыс екенін көрсетеді.
Сонымен теңсіздік
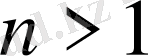 үшін дұрыс болады деген жорамалымызды дәлелдедікте.
үшін дұрыс болады деген жорамалымызды дәлелдедікте.
Мысал 2. Берілген теңсіздіктен қатені табу керек.
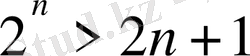
n- натурал сандар.
Шешімі:
n=k үшін теңсіздік дұрыс деп алып
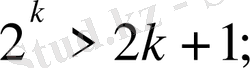 (1) .
(1) .
n=k+1 үшін теңсіздікті тексеріп көрейік. Онда:
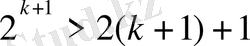 ;
;
Шынында
 саны кезкелген натурал сандар үшін 2 ден үлкен болалмайды.
саны кезкелген натурал сандар үшін 2 ден үлкен болалмайды.
Міне қателік табылды. Нақтылап айтқанда:
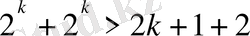 немесе
немесе
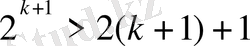 . Сонымен қателік табылды.
. Сонымен қателік табылды.
Тек
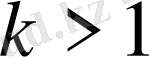 натурал саны үшін орындалады.
натурал саны үшін орындалады.
Мысал 3.
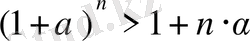 ;
;
теңсіздігін дәлелдеу керек. Егер мына шарттарды қанағаттандырса:
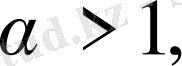
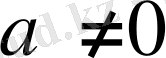 , n натурал сандар және бірден кіші емес.
, n натурал сандар және бірден кіші емес.
Шешімі:
1) . n=2 үшін
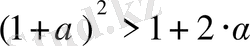

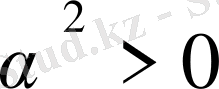
теңсіздігі орындалады.
2) . n=k үшін
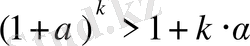 (1) .
(1) .
теңсіздігін дұрыс деп ұйғарып n=k+1 үшін
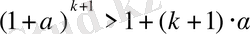 (2) .
(2) .
теңсіздігін дәлелдейік. Шынында
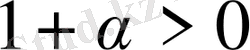 шарты пайдаланып (1) - өрнектің екі жағын да
шарты пайдаланып (1) - өрнектің екі жағын да
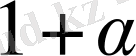 санына көбейтейік. Сонда:
санына көбейтейік. Сонда:
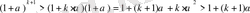
орындалады. Себебі
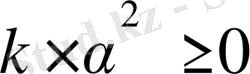 болады. Сонымен (2) өрнектегі теңсіздіктің дұрыстығын дәлелдедік. Ал ол дегеніміз
болады. Сонымен (2) өрнектегі теңсіздіктің дұрыстығын дәлелдедік. Ал ол дегеніміз
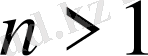 натурал сандары үшін де теңсіздік дұрыс орындалады.
натурал сандары үшін де теңсіздік дұрыс орындалады.
Мысал 4.
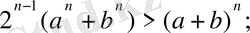 (1) .
(1) .
теңсіздігін дәлелдеу керек, егер
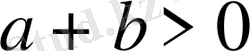 ,
,
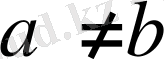 , n натурал сан және бірден үлкен болса.
, n натурал сан және бірден үлкен болса.
Шешімі:
1) . n=2 үшін (1) - өрнектен теңсіздіктің мына түрдегісін көреміз:
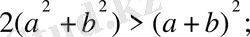 (2) .
(2) .
Сондай-ақ
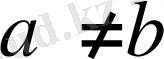 шартынан (2) - өрнек мына түрге келеді:
шартынан (2) - өрнек мына түрге келеді:
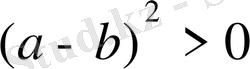 (3) .
(3) .
Және бұл дегеніміз кез-келген санның квадраты нөлден үлкен деген сөз. Расында кез-келген санның квадраты оң сан, оң сан дегеніміз нөлден үлкен сан. (3) - өрнектектің сол жағы оң сан және нөлден үлкен сан болады.
Бұнымен n=2 үшін (1) - өрнектегі теңсіздік дұрыс екендігін дәлелдедік.
2) . n=k үшін (1) - өрнек дұрыс деп
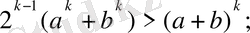 (4) .
(4) .
n=k+1 үшін
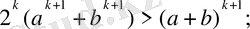 (5) .
(5) .
теңсіздігін дәлелдесек. Сонымен (4) - өрнектің екі жағын да a+b ға көбейтейік. Сонда:
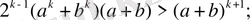 (6) .
(6) .
(5) - өрнектегі теңсіздікті дәлелдеу үшін жәй ғана мына теңсіздікті дәлелдесек болғаны:
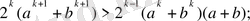 (7) .
(7) .
немесе маңызды теңсіздік:
 (8) .
(8) .
(8) - теңсіздіктен мына теңсіздік шығады:
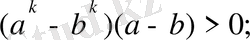 (9) .
(9) .
Егер
 болса, онда
болса, онда
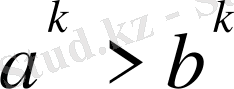 болады. (9) - өрнектегі теңсіздікке қоятын болсақ теңсіздік дұрыс орындалады. Ал егер
болады. (9) - өрнектегі теңсіздікке қоятын болсақ теңсіздік дұрыс орындалады. Ал егер
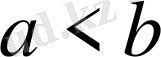 болса, онда
болса, онда
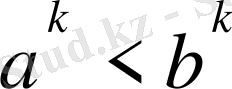 болады. Бұдан
болады. Бұдан
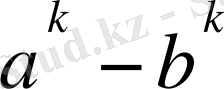 ,
,
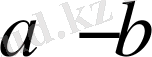 екеуі теріс сан болады, бірақ көбейтіліп оң сан болып кетеді. Сонымен (9) - өрнектегі теңсіздік дұрыс екенін дәлелдедік. Онда (9) - өрнектегі теңсіздік дұрыс болса, (8) - өрнектегі теңсіздікте дұрыс болғаны. (8) - өрнектегі теңсіздік дұрыс болса онда (7) - өрнектегі теңсіздікте
екеуі теріс сан болады, бірақ көбейтіліп оң сан болып кетеді. Сонымен (9) - өрнектегі теңсіздік дұрыс екенін дәлелдедік. Онда (9) - өрнектегі теңсіздік дұрыс болса, (8) - өрнектегі теңсіздікте дұрыс болғаны. (8) - өрнектегі теңсіздік дұрыс болса онда (7) - өрнектегі теңсіздікте
дұрыстығы шығады. Сонымен n>1 үшін (1) - өрнектегі теңсіздік дұрыс екенін дәлелдедік.
2. 3. Математикалық индукция әдісін басқа есептерде қолдану.
Математикалық индукция әдісімен төмендегі өте маңызды тұжырымды дәлелдейік.
Теорема.
Егер саны n саны болатын
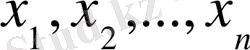 оң сандардың көбейтіндісі бірге тең болса, онда олардың қосындысы сол n санынан кем болмайды, яғни
оң сандардың көбейтіндісі бірге тең болса, онда олардың қосындысы сол n санынан кем болмайды, яғни
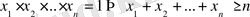
Дәлелдеу.
Алдымен n=2 болғанда тұжырымның орынды екенін, яғни
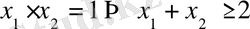
дәлелдейік. Мұнда екі жағдайда қарастырамыз:
1.
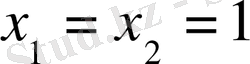 ,
,
онда
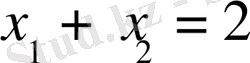 болып тұжырым орындалады.
болып тұжырым орындалады.
2.
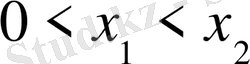 ,
,
Бұл жағдайда
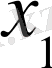 мен
мен
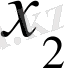 көбейтіндісі бірге тең болғандықтан
көбейтіндісі бірге тең болғандықтан
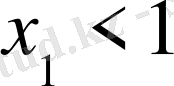 , ал
, ал
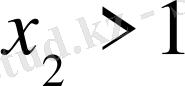 деп алуға болады.
деп алуға болады.
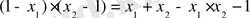
теңдіктен
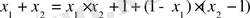 (1) .
(1) .
Енді
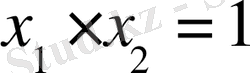 екендігін ескеріп
екендігін ескеріп
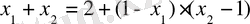
аламыз. Бұдан
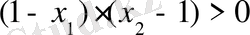 болғандықтан
болғандықтан
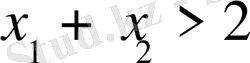 шығады.
шығады.
Сөйтіп n=2 болғанда тұжырым дәлелденді. Сонымен қатар

Болғанда ғана
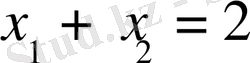 теңдігін орындалатынын, ал
теңдігін орындалатынын, ал
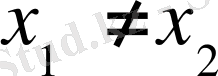
болса
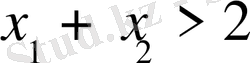 байқаймыз.
байқаймыз.
Енді математикалық индукция принципі бойынша тұжырымды
n=k үшін орынды
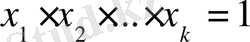
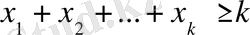
деп жорып, n=k+1 үшін
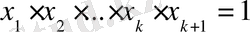 болғанда /
болғанда /
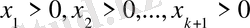 үшін /
үшін /
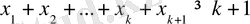
екенін дәлелдейміз.
Алдымен
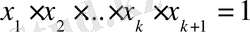 болғандықтан төмендегі екі жағдай болуы мүмкүн екендігін байқаймыз:
болғандықтан төмендегі екі жағдай болуы мүмкүн екендігін байқаймыз:
1/ барлық
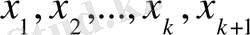 көбейткіштер өзара тең
көбейткіштер өзара тең
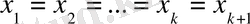 .
.
2/ көбейткіштердің барлығы бірдей өзара тең емес.
Бірінші жағдайда әрбір көбейткіш бірге тең болар еді де, олардың қосындысы k+1 -ге тең болады.
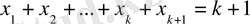 ;
;
Екінші жағдайда
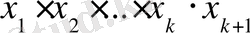 көбейтіндінің көбейткіштерінің ішінен бірден үлкені де, кішісі де табылады /себебі барлық көбейткіш бірден кіші болса олардың көбейтіндісі бірден кіші болар еді /.
көбейтіндінің көбейткіштерінің ішінен бірден үлкені де, кішісі де табылады /себебі барлық көбейткіш бірден кіші болса олардың көбейтіндісі бірден кіші болар еді /.
Мысалы,
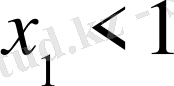 , ал
, ал
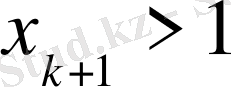 болсын. Онда көбейтіндіні
болсын. Онда көбейтіндіні
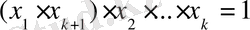
түрде жазып,
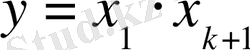 деп алсақ
деп алсақ
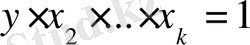 болады. Мұнда k оң сандардың көбейтіндісі бірге тең болғандықтан жоруымыз бойынша олардың қосындысы k -дан кем емес, яғни
болады. Мұнда k оң сандардың көбейтіндісі бірге тең болғандықтан жоруымыз бойынша олардың қосындысы k -дан кем емес, яғни
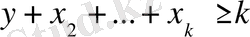
Олай болса
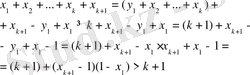
Мысал 1.
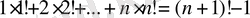 (1) .
(1) .
Тепе- теңдікті дәлелдейік.
Шешімі:
n!=1·2·3·…·n екендігін ескеріп, n=1 деп алсақ 1·1=(1+1) !-1, бұдан 1=1.
n=k болғанда
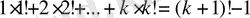
теңдігі орындалады деп алып
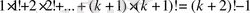
оның n=k+1 болғанда ғы дұрыстығын көрсетейік:
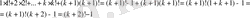
болып (1) өрнектегі теңдік орынды екені келіп шығады.
Мысал 2.
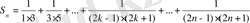 (1) .
(1) .
Қосындыны есептейтін формуланы қорытайық.
Шешімі:
Мұндағы n -інші қосылғышты
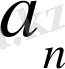 арқылы белгілейік:
арқылы белгілейік:
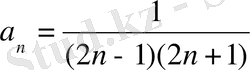
Алдымен математикалық индукция әдісімен төмендегі өрнектің орынды екенін дәлелдейік:
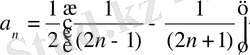 (2) .
(2) .
Шынында, n=1 болсын
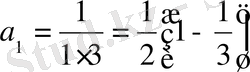
(2) өрнек орынды. Енді n=k үшін болғанда (2) орындалсын дейік, яғни
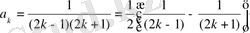
n=k+1 болғанда (2) орынды екенін дәлелдеу үшін
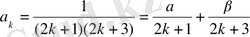 (3) .
(3) .
Деп алайық, мұндағы
 мен
мен
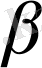 белгісіз сандар. Ол сандарды (3) теңдіктен табамыз
белгісіз сандар. Ол сандарды (3) теңдіктен табамыз
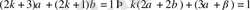
Бұдан k -нің коэффициенттерін теңестіріп
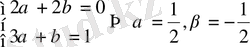 табамыз.
табамыз.
Сонымен, (3) өрнекті былай жазуға болады
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz