Көпжақтардың жазықтықпен және түзумен қиылысуы: теория, проекциялар және қолданбалар


Көпжақтар
Жоспары
Кіріспе
1. 1. Көпжақтың жазықтықпен қиылысуы . . . 3
1. 2. Көпжақтың түзумен қиылысуы . . . 4
1. 3. Екі көпжақтың қиылысу сызығы . . . 6
1. 4. Тәжірибеде көпжақтардың қиылысу сызығын анықтау . . . 9
Қорытынды . . . 14
Қолданылған әдебиеттер . . . 16
Кіріспе
Кеңістікте орналасқан, жазықтықтардың жиынтығынан құрылған, кеңістікті шектейтін бітеу біртұтас геометриялық денені көпжақты беттер дейді. Көпжақты бет дегеніміз - табандары үш немесе одан да көп көпбұрыштардың жиынтығынан құралған геометриялық фигура. Көпжақты беттердің жақтары мен қырлары жəне төбелері болады. Көпжақты беттердің жақтары дегеніміз - беттердің жазықтық болып келетін жағы. Ал көпжақты беттердің қырлары деп беттердің жақтарымен қиылысқан сызығын айтады. Көпжақты беттердің қырлары өзара қиылысып, беттердің төбелерін береді. Көпжақты беттер жақтарының, қырлары мен төбелерінің өзара орнала- суларына байланысты жай жəне дұрыс болып екі түрге бөлінеді.
Дұрыс көпжақты бет деп жақтарының бұрыштары мен аудандары өзара тең болатын беттерді айтады. Кей жағдайда бұл беттерді Платон денелері деп атайды, себебі Платон бұл көпжақтарды зерттеп, олардың атын Алтыншы тарау КӨПЖАҚТЫ БЕТТЕР П0 a) c) b) d) e) 72 қойған. Беттердің жақтарының сандарына байланысты көпжақты беттер төмендегі түрлерге бөлінеді: тетраэдр (жақтары өзара тең үшбұрыш болатын төрт жақты көпжақты бет) октаэдр (жақтары өзара тең үшбұрыш болатын сегіз жақты көпжақты бет) икосаэдр (жақтары өзара тең үшбұрыш болатын жирма жақты көпжақты бет) гексаэдр (жақтары өзара тең төртбұрыш болатын алты жақты көпжақты бет) ) жəне додекаэдр (жақтары өзара тең бесбұрыш болатын он екі жақты көпжақты бет) Жай көпжақты беттер жақтарына байланысты призма (жақтары өзара перпендикуляр орналасқан), пирамида (жақтары бір ғана нүктеге ұмтылатын) жəне призматоид (табаны мен үсті өзара параллель орналасқан, жақтары үшбұрыш немесе трапеция болатын) болып бөлінеді.
- КӨПЖАҚТАР
Көпжақ деп жазық көпбұрыштармен шектелген денені айтамыз. Көпжақтарды шектейтін көпбұрыштарды жақтар деп, ал олардың ортақ қабырғаларын қырлар деп атайды. Қырлардың ортақ нүктелерін төбелер деп аталады.
Көп тараған көпжақтар - призмалар және пирамидалар. Екі жағы табандары деп аталатын параллель көпбұрыштар болатын, қырлары табанына перпендикуляр призманы тік призма деп атайды. Егер тік призманың табаны - тік төртбұрыш болса, оны параллелепипед деп атайды.
Бір жағы - кез келген көпбұрыш болатын, ал қалған жақтары - ортақ төбесі бар үшбұрыш болатын көпжақты пирамида деп атайды.
Көпжақтардың көптеген түрлерінің ішінен ерекше топты дұрыс дөңес көпжақтар құрайды. Дұрыс көпжақтар (Платон денелері) деп жақтары - дұрыс және тең көпбұрыштар, ал төбе бұрыштары тең болатын көпжақтарды атаймыз. Әр дұрыс көпжаққа сырттай немесе іштей сфераны салуға болады.
Бес дұрыс көпжақтар бар:
1. Тетраэдр (төртжақ) бірдей төрт теңқабырғалы үшбұрыштармен шектелген.
2. Гексаэдр (алтыжақ) немесе куб . Оның беті алты тең квадраттардан тұрады.
3. Октаэдр (сегізжақ) . Оның беті сегіз бірдей теңқабырғалы үшбұрыштардан тұрады. Куб және октаэдрдің қырларының саны бірдей. Октаэдрға кубты салуға болады, ал кубқа октаэдрді бір көпжақтың төбелері екіншісінің бүйірінің центрімен сәйкес болатындай салуға болады. Бұндай көпжақтарды өзара сәйкес деп атайды.
4. Додекаэдр (он екі жақ) бірдей және дұрыс бесбұрыштармен шектелген. Әр төбеге үш бесбұрыш қосылған. Додекаэдрге дұрыс жиырмажақ сәйкес келеді.
5. Икосаэдр (жиырмажақ) . Оның беті жиырма бірдей теңқабырғалы үшбұрыштардан құралған, және әрбір төбесі бес үшбұрышты біріктіреді. Икосаэдрге додекаэдрді салса болады. Икосаэдр және додекаэдр өзара сәйкес көпжақтар болып табылады. Тетраэдр өзіне өзі сәйкес келеді.
Әрбір өзара сәйкес көпжақтар жұбының біреуінің жақтар саны, екіншісінің төбелер санына сәйкес келеді, ал қырларының саны тең болады. Дөңес көпжақтардың барлық түрлерінің жақтарының саны (Ж), төбелерінің (Т) және қырларының (Қ) сандарының қатынасын Эйлер жазды:
Кез келген дөңес көпжақтың жақтары мен төбелерінің санының қосындысынан қырлар санының айырмасы екіге тең, яғни
Ж + Т - Қ =2.
Көпжақтын қырларының көрінетіндігі.
Көрінетіндікті анықтау үшін бәсекелес нүктелер әдісі қолданылады (1. 1-сурет) . Көпжақтың проекциясының сыртқы қырлары әрдайым көрінеді. Контурдың ішіндегі қырлардың көрінетіндігін әрбір проекцияда қырлардың өзара орналасуын пайдалана отырып, бөлек анықтау керек.
1. 1-суретте төртжақтың проекциялары берілген. 1 және 2 нүктелері - фронталь-бәсекелес, ал 3 және 4 нүктелері - горизонталь-бәсекелес. Бәсекелес нүктелердің өзара орналасуына қарап фронталь проекцияда АD қыры көрінетінін, ал ВС қырының көрінбейтінін анықтаймыз.
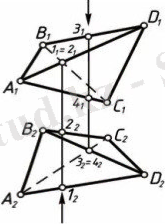
1. 1-сурет
Горизонталь проекцияда BD қыры көрінетін, ал АС - көрінбейтін қыр болады.
1. 1. Көпжақтың жазықтықпен қиылысуы
Көпжақ бетінің жазықтықпен қимасы - жазық көпбұрыш болып табылады. Оның төбелері мен қабырғалары - берілген жазықтықтың берілген көпжақтың жақтарымен және қырларымен қиылысуымен анықталады. Сондықтан қиманы тұрғызу үшін екі түрлі тәсіл қолданылады:
1) қырлар тәсілі - берілген жазықтықтың көпжақ қырларымен қиылысу нүктелерін, яғни қиманың төбелерін табады;
2) жақтар тәсілі - жазықтықтың көпжақ жақтарымен қиылысу түзулерін, яғни қиманың қабырғаларын тұрғызады.
Жақтар тәсілін көпжақ жақтарының проекциялаушы жазықтықтар болған кезінде қолданған тиімді.
Көпжақтың жазықтықпен қимасын табуға бірнеше мысалдар қарастырып көрелік.
1-мысал. Көпжақтың проекциялаушы жазықтықпен қиылысуы. Қиюшы жазықтық проекциялаушы болса, қиманы табу жеңіл. Бұл жағдайда қиманың бір проекциясы проекцияланатын ізбен сәйкес болады. 1. 2-суретте SABC пирамидасының α(α1) фронталь-проекциялаушы жазықтығымен қиылысуы көрсетілген. Қиюшы жазықтық пирамиданың бүйір қырларын D, E, F нүктелерінде қияды: α∩(SA) =D, α∩(SB) =E, α∩(SC) =F. DEF қимасының D1E1F1 фронталь проекциясы қиюшы жазықтықтықтың α1 фронталь ізімен сәйкес болады. Байланыс сызықтарын жүргізіп, қиманың D2E2F2 горизонталь проекциясын табамыз.
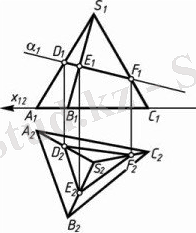
1. 2-сурет
2-мысал. Тік призма мен жалпы жағдайдағы жазықтықтың қиылысуы. 1. 3-суретте тік призма мен қиылысатын екі түзумен берілген α f∩h) жазықтығымен қиылысуы көрсетілген.
1. 3-сурет
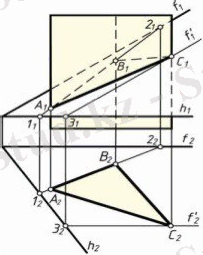
Призманың бүйір жақтары - горизонталь проекциялаушы жазықтықтар болғандықтан қиманың горизонталь проекциясы A2B2C2 белгілі - ол бүйір жақтарының және қырларының проекцияларымен сәйкес болады. Қиманың фронталь проекциясын тұрғызу үшін қиюшы жазықтыққа тиісті А, В, С нүктелерінің фронталь проекцияларын анықтау қажет. А2 және В2 нүктелері арқылы (1, 2) түзуінің - горизонталь (1222) проекциясын жүргізеді. (1, 2) түзуінің фронталь (1121) проекциясында А1, В1 фронталь проекцияларын табамыз. С нүктесінің фронталь проекциясын табу үшін алдымен C2 арқылы f´ фронталінің f´2 горизонталь проекциясын жүргізеді. Ол α жазықтығының h горизонталінің h2 горизонталь проекциясымен қиылысады: f´2∩h=32. f´ фронталінің f´1 фронталь проекциясы 31 нүктесі арқылы f фронталінің f1 фронталь проекциясына жүргізеді. f´1 түзуі призманың сәйкес қырымен қиылысқанда С нүктесінің ізделініп отырған С1 проекциясын табылады.
3-мысал. Пирамиданың жалпы жағдайдағы жазықтықпен қиылысуы.
Көпжақтың жалпы жағдайдағы жазықтықпен қимасын анықтағанда оның екі проекциясын да тұрғызу қажет (1. 4-сурет) . Қиюшы жазықтықтың горизонталь ізі пирамиданың табанын қимайды, сондықтан оның тек бүйір жақтары қиылады. Қиманың пішіні үшбұрыш болуы керек, пирамида қырларының жазықтықпен қиылысу нүктелері - үшбұрыштың төбелері болады.
SC қырының α(f∩h) жазықтықпен D қиылысу нүктесі - фронталь проекциялаушы β(β1) жазықтығының көмегімен табылады. Осындай тәсілмен, қиманың Е нүктесін де табуға болады. Алайда, басқа тәсілді де қолданса болады. Қиюшы α жазықтығының h горизонталі пирамида табанының жазықтығында орналасқан. Сондықтан пирамиданың SАС жағының ізі болып табылатын АС қыры қиюшы жазықтықтың горизонталь ізімен қиылысады. А2С2 түзуінің h2 түзуімен қиылысу нүктесін табады: (А2С2) ∩h2=32. D және 3 нүктелері SАС жазықтығы мен α қиюшы жазықтығының қиылысу сызығына тиісті. D232 түзуінің S2A2 түзуімен қиылысу нүктесін табады: (D232) ∩(S2 A2) =E2. Байланыс сызығы бойымен Е нүктесінің фронталь проекциясын табады.
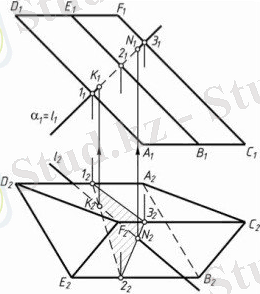
1. 4-сурет
F нүктесін осындай әдіспен тұрғызады, себебі SB қыры арқылы жүргізілген қосымша қиюшы проекциялаушы жазықтық проекцияның профиль жазықтығына параллель болады да, ешқандай шешімге алып келмейді. 4 нүктесі SAB жазықтығының горизонталь ізі мен α қиюшы жазықтығының қиылысу нүктесі болып табылады: (А2В2) ∩h2=42. Е және 4 нүктелері SAB жазықтығы мен α қиюшы жазықтығының қиылысу сызығына тиісті. Е242 түзуінің S2В2 түзуімен қиылысу нүктесін табады: (Е242) ∩(S2В2) =F2. Байланыс сызығы бойымен F нүктесінің фронталь проекциясын табады. DEF үшбұрышы ізделінді қима болып табылады.
1. 2. Көпжақтың түзумен қиылысуы
Көпжақтың түзумен қиылысу нүктелерін табу есебі үш қадамда шешіледі:
- берілген түзу арқылы қиюшы жазықтықты жүргізеді;
2) қиюшы жазықтық пен көпжақтың қиылысу сызығын тұрғызады;
3) берілген түзудің қима контурымен қиылысу нүктелері ізделінді нүктелер болып табылады.
1. 5-суретте үшбұрышты көлбеу призманың l түзуімен қиылысу нүктелері табылған. Алдымен l түзуі арқылы фронталь-проекциялаушы α(α1) жүргізілген. Призма мен α жазықтығының қиылысу сызығы тұрғызылған. Ол үшін призма қырларының α жазықтығымен қиылысу нүктелері табылған: 1=l∩(AD), 2=l∩(BE), 3=l∩(CF) . Қиылысу сызығының фронталь проекциясы l түзуінің l1 фронталь проекциясымен беттеседі. Қиылысу сызығының горизонталь проекциясы l түзуінің l2 горизонталь проекциясымен K2 және N2 нүктелерінде қиылысады. Байланыс сызықтары арқылы ізделінді нүктелердің K1 және N1 фронталь проекциялары табылған.

1. 5-сурет
1. 3. Екі көпжақтың қиылысу сызығы
Екі көпжақтың қиылысу сызығы кеңістік тұйық сынық болып табылады. Кейбір ерекше жағдайларда бұл сынық екі тұйық сыныққа бөлінуі мүкін. Бір көпжақтың қырларының екінші көпжақтың беттерімен қиылысу нүктелері сынықтың төбелері болып табылады. Сынықтың қабырғалары - түзу кесінділері болып табылады, олар арқылы көпжақтардың беттері қиылысады. Егер қиылысатын екі көпжақтың біреуінің жақтары мен қырлары проекциялаушы болса, есепті шешу жеңіл болады. 5. 6- суретте көрсетілген мысалда пирамидамен қиылысатын призманың бүйір жақтары мен қырлары горизонталь- проекциялаушы. Призманың бүйір қырлары нүктелерге проекцияланады, ал бүйір беттері горизонталь проекциялаушы жазықтықтарды анықтайды. Пирамида қырларының призмамен қиылысу нүктелері горизонталь проекцияда анықталып, байланыс сызықтары арқылы нүктелердің фронталь проекциялары тұрғызылады:
1 = (SA) ∩ (EHRF), 2 = (SB) ∩ (EHRF), 3 = (SC) ∩ (EHRF),
4 = (SC) ∩ (DQHE), 5 = (SB) ∩ (DQHE), 7 = (SA) ∩ (DQGT) .
Табандары бір жазықтықта орналасқан екі көпжақтың қиылысу сызығын тұрғызу кезінде, көмекші жазықтық ретінде көбінесе жалпы жағдайдағы жазықтықтарды пайдаланған тиімді:
1) екі пирамида - көмекші жазықтықтар пирамидалар төбелерімен өтуі тиіс;
2) пирамида және призма - көмекші жазықтықтар призманың бүйір қырларына параллель болуы керек және пирамида төбесінен өтуі қажет;
3) екі призма - көмекші жазықтықтар екі призманың бүйір қырларына параллель болуы керек.
1. 6-сурет
1. 7 - суретте табандары бір жазықтықта жататын SABC және PDEF пирамидаларының қиылысу сызығын табу көрсетілген. Пирамидалардың бүйір қырлары мен жақтарының қиылысу нүктелерін анықтау үшін олардың төбелері арқылы SP түзуі жүргізіліп, оның горизонталь ізі K нүктесі табылған. SP түзуі арқылы өтетін көмекші жазықтықтар көпжақтардың жақтарын түзулер бойымен қияды және ол жазықтықтардың горизонталь іздері K нүктесі арқылы өтеді. K2 нүктесі АВС және DEF үшбұрыштарының орналасуына байланысты пирамидалардың қиылысатынын немесе қиылыспайтынын, қиылысса қай қырларының екінші көпжақпен қиылысатынын анықтауға болады. Пирамидалардың табандары L, M, V, R, T, G нүктелерінде қиылысады. Ал қырлардың ішінде РD және РЕ қырлары ғана SABC пирамидасын қияды.
РD қырының SABC пирамидасымен қиылысу нүктесін табу үшін SP және РD түзулері арқылы көмекші жазықтық тұрғызылады. Көмекші α(SP∩РD) жазықтығы SABC пирамидасының SAB жағын S1 түзуі бойымен, ал SAC жағын S2 түзуі бойымен қияды: α∩( SAB) =(S1), α∩(SAC) =(S2) . РD қыры S1 және S2 түзулерімен N және H нүктелерінде қиылысады: (РD) ∩(S1) =N, (РD) ∩(S2) =H. Бұл нүктелер РD қырының SAB және SAC жақтарымен қиылысу нүктелері болып табылады: N=(РD) ∩(SAB), H=(РD) ∩(SAC) .
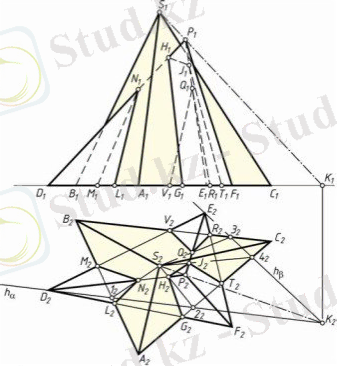
1. 7-сурет
РЕ қырының SABC пирамидасымен қиылысу нүктесін табу үшін SP және РЕ түзулері арқылы көмекші жазықтық тұрғызылады. Көмекші β(SP∩РE) жазықтығы SABC пирамидасының SBC жағын S3 түзуі бойымен, ал SAC жағын S4 түзуі бойымен қияды: β∩(SBC) =(S3), β∩(SAC) =(S4) . РE қыры S3 және S4 түзулерімен Q және J нүктелерінде қиылысады: (РE) ∩(S3) =Q, (РE) ∩(S4) =J. Бұл нүктелер РE қырының SBC және SAC жақтарымен қиылысу нүктелері болып табылады: Q=(РE) ∩(SBC), J=(РE) ∩(SAC) . Пирамидалардың жақтарының қиылысу сызықтарын салу үшін N, H, Q, J нүктелерінен табандардың қиылысу нүктелеріне кесінділер жүргізеді. LNM, GHJT, VQR көпбұрыштары SABC және PDEF пирамидаларының қиылысу сызығы болады.
1. 4. Тәжірибеде көпжақтардың қиылысу сызығын анықтау
Сәулет пен құрылыста көпжақтар кеңінен қолданылады. Ғимараттардың сыртқы пішімі, олардың құрылымдық элементтері көбінесе көпжақтар (призмалар, параллелепипедтер, пирамидалар және т. б. ) болып келеді. Ғимараттардың шатырлары, кеңістік жабындары да әртүрлі көпжақты беттер болып келеді.
Шатыр құламаларының қиылысу сызықтарын салу. Сәулет- құрылыс жобаларында міндетті түрде шатыр жабынының жоспары орындалады. Осы кезде шатыр құламаларының қиылысу сызықтарын салу керек болады. Көбінесе шатыр құламаларының көлбеулік бұрыштары бірдей, ал олардың төменгі ернеулері бір деңгейде болады. 1. 8-суретте планда тіктөртбұрыш болып келетін үйдің шатыр жабынының проекциялары көрсетілген.
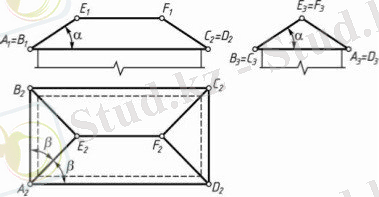
1. 8-сурет
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz