Айналдыру әдісі

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:

Айналдыру әдісі

Жоспары

Кіріспе

1. Сызбаны түрлендіру тәсілдері . . . 3

1. 2. Жазық-параллель ығыстыру тәсілі . . . 4
1. 3. Сызбаны түрлендірумен шығарылатын негізгі есептер . . . 6
1. 4. Проекциялаушы түзуден айналдыру тәсілі . . . 9
1. 5. Деңгейлік түзуден айналдыру тәсілі . . . 10
1. 6. Проекциялар жазықтықтарын алмастыру тәсілі . . . 12

Қорытынды . . . 14

Қолданылған әдебиеттер . . . 16

Кіріспе

Эпюрде геометриялық фигуралардың нақты шамаларын графикалық

тәсілмен анықтауды метрлік есептер шығару дейді.

Эпюрді түрлендіру үшін: берілген геометриялық элементтер мен

проекциялар жазықтықтарының өзара орналасуын немесе проекциялау

бағытын өзгертуге болады. Геометриялық элементтердің проекциялар

жазықтықтары жүйесіне қатысты орналасуын өзгертуге мынадай тәсілдер

көмегімен атқарылады.

Берілген проекциялар жазықтықтары жүйесіне басқа жазықтық енгізіп,

кескінделген нәрсенің дербес жағдайын алу - проекциялар жазықтықтарын

алмастыру тәсілі;

обьектіні кеңістікте қозғай отырып, дербес жағдайға әкелу - жазық параллель

жылжыту және айналдыру тәсілдері.

Тәсілдің негізгі мәні мынада: нүктелердің, түзулердің, жазықтықтардың

кеңістіктегі орны өзгермейді, ал олар қажет жағдайда болу үшін берілген

проекциялар жазықтықтарының біреуі немесе екеуі біртіндеп басқа

жазықтықтарымен алмастырылады. Жаңадан енгізілген проекциялар

жазықтығы ескі жүйедегі проекциялар жазықтықтарының біреуіне

перпендикуляр болуы шарт.

“Аксонометрия” - грек тілінде осьтер бойынша өлшеу деген сөз.

Аксонометриялық проекцияның ортогональ проекциядан негізгі бір

артықшылығы оның көрнектілігі мен өлшеуге қолайлылығында. Сондықтан

аксонометриялық проекциялар кескіндеу техникасында өте кеңінен тараған.

Ортогональ проекцияларда геометриялық денелердің проекциялары негізінен

өзара перпендикуляр екі жазықтыққа түсірілетін. Бұдан алынған проекция

заттың кескінің көрнекті түрде береді, өйткені ол заттың көлемдік проекциясын оңай елестететін үш өлшемінде: биіктігін, ұзындығын және енін бейнелейді.

СЫЗБАНЫ ТҮРЛЕНДІРУ ТӘСІЛДЕРІ

Берілген проекциялары бойынша фигураның жаңа проекцияларын салуды сызбаны түрлендіру деп атайды. Сызбаны түрлендіру екі әдіспен жасалады:

1. Фигураның негізгі π1, π2, π3 проекциялар жазықтықтарына қатысты орнын өзгерту арқылы сызбаны түрлендіру.

2. Қосымша проекциялар жазықтығын енгізу арқылы сызбаны түрлендіру. Проекциялар жазықтықтарын алмастыру тәсілі осы әдіске негізделген.

Фигураның негізгі π1, π2, π3 проекциялар жазықтықтарына қатысты орнын өзгерту арқылы сызбаны түрлендіру әдісінде фигураны есепті шығаруға қолайлы болатындай етіп орналастырады. Фигураның қозғалысына байланысты мынадай тәсілдер болады:

а) жазық-параллель ығыстыру тәсілі;

б) проекциялаушы түзуден айналдыру тәсілі;

в) деңгейлік түзуден айналдыру тәсілі.

1. 1 Жазық-параллель ығыстыру тәсілі

Жазық-параллель ығыстыру деп фигураның нүктелері өзара параллель жазықтықтарда орындарын өзгертетіндей етіп қозғауды айтады. Көбіне проекциялар жазықтықтарының біреуіне параллель бағытта жазық-параллель ығыстыру тәсілін қолданады.

Сызбада фигураның соңғы орнын анықтау үшін түрлендірудің инварианттарын білу керек. Фигураның берілген проекциялары бойынша оның жаңа проекциясын салуға мүмкіндік беретін қасиеттерді түрлендірудің инварианттары деп атайды.

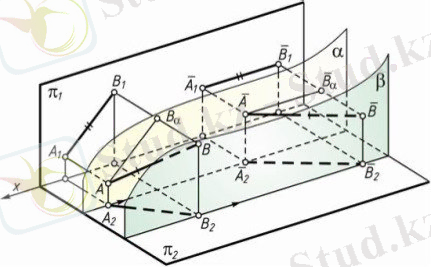
1. 1-сурет

1. 1-суретте АВ кесіндісін π₁ проекциялар жазықтығына параллель жазықтықтарда жазық-параллель жылжыту көрсетілген. А нүктесі α жазықтығында, В нүктесі β жазықтығында қозғалып, АВ кесіндісі π₂ проекциялар жазықтығына параллель орналастырылады. Сонда АВ кесіндісінің π₁ проекциялар жазықтығындағы проекциясы өзінің пішімі мен өлшемдерін сақтап орнын ауыстырады. Ал АВ кесіндісінің π₂ проекциялар жазықтығындағы проекциясы x осіне параллель түзулердің бойымен қозғалады. В нүктесінің α жазықтығындағы проекциясын Вα деп белгілейік. Сонда ( А₁В₁ ) ( A Вα) және А₁В₁ = A Вα болады. АВ кесіндісін π₂ проекциялар жазықтығына параллель етіп орналастырғанда АВ = АВ, ВВα = ВВα, АВα = АВα = А₁В₁ , яғни А₁В₁ = А₁В₁ болады. Ал (А₂ А₂) және (В₂ В₂) түзулері x осіне параллель болады. Дәл осылай π₂ проекциялар жазықтығына параллель жазықтықтарда жазық-параллель жылжытуға болады.

Сонымен жазық-параллель ығыстыру тәсілінің инварианттары мынадай болады:

1) қозғалу бағытына параллель жазықтықтағы проекция өзінің пішінін және өлшемдерін сақтап орнын ауыстырады;

2) нүктелердің қозғалу бағытына перпендикуляр жазықтықтағы проекциялары проекциялық байланыс сызықтарына перпендикуляр түзулердің бойымен қозғалады.

Сызбаны түрлендірумен шығарылатын негізгі есептер

Сызбаны түрлендірумен шығарылатын барлық есептер негізгі төрт есепті шығаруға келіп тіреледі. Осы есептерді жазық-параллель ығыстыру тәсілімен шығарып көрсетейік.

1-есеп. Жалпы жағдайдағы түзуді деңгейлік жағдайға келтіру.

Егер біз l түзуін горизонталь жағдайға келтіргіміз келсе, онда оны π1 жазықтығына қатысты жазық-параллель ығыстыру керек. (1. 2-сурет) . Түзудің бойынан қалауымызша А және В нүктелерін таңдап аламыз. Көлденең түзу салып, оның бойына А´₁В´₁ кесіндісін саламыз: А´₁ В´₁ = А₁В₁ . Оны l´ горизонталь түзуінің жаңа l´₁ фронталь проекциясы реті$нде қабылдаймыз. А және В нүктелерінің жаңа горизонталь проекциялары А₂ және В₂ нүктелері арқылы өтетін көлденең түзулердің бойында табылады. Жаңа А´₁ және В´₁ фронталь проекциялары арқылы А´₂ және В´₂ горизонталь проекцияларын анықтаймыз. Егер l түзуін фронталь еткіміз келсе, оны π₂ жазықтығына қатысты жазық-параллель ығыстыру керек (1. 2-сурет) . Бұл есепті шығару нәтижесінде біз l түзуінің АВ кесіндісінің нақты шамасын (А₂ ' В₂' = A₁ B₁ = AB) және оның π₁ мен π₂ жазықтықтарына көлбеулік α мен β бұрыштарын таптық.

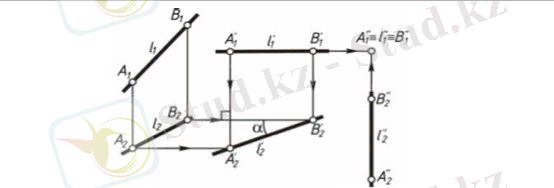
1. 2-сурет

2-есеп. Деңгейлік түзуді проекциялаушы жағдайға келтіру.

Егер l´(l₁´, l₂´) горизонталь түзуі берілсе, оны фронталь проекциялаушы l´´ түзуіне түрлендіру жеңіл (1. 2-сурет) . Ол үшін тік түзу жүргізіп, оның бойына А₂″В₂″ кесіндісін саламыз : А₂″В₂″= А´₂ В´₂ . Оны l₂″ фронталь проекциялаушы түзуінің горизонталь проекциясы ретінде қабылдаймыз. Түзудің l₁″ фронталь проекциясы нүктеге проекцияланады: А₁″≡В₁″≡l₁″.

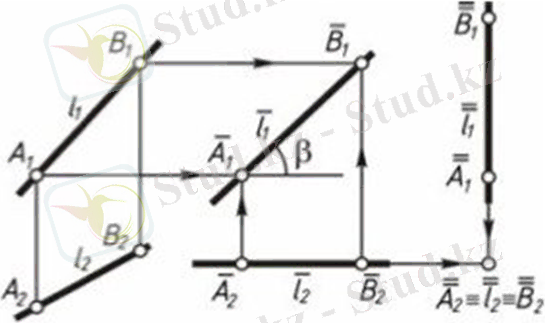
1. 3-сурет

Фронталь l(l ₁, l₂) түзуін горизонталь проекциялаушы l түзуіне түрлендіру ыңғайлы (1. 3-сурет) . Алдымен түзудің жаңа l₁ фронталь проекциясын тік салып, содан соң нүктеге проекцияланатын горизонталь проекциясын саламыз.

3-есеп. Жалпы жағдайдағы жазықтықты проекциялаушы жағдайға келтіру.

Егер α(АВС) жазықтығын горизонталь проекциялаушы жағдайға келтіру керек болса, онда оны π₁ жазықтығына қатысты жазық-параллель ығыстыру қажет (1. 4- сурет) .

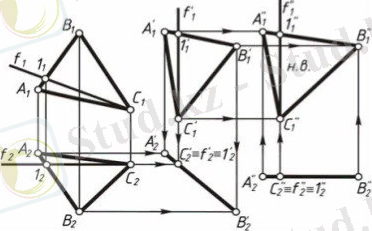
1. 4-сурет

Алдымен α жазықтығының f фронталін жүргізіп, оны горизонталь проекциялаушы f ´ түзуіне түрлендіру керек. АВС үшбұрышының жаңа А´₁ В´₁ С´₁ фронталь проекциясын f₁´ тік орналасатындай етіп саламыз, мұндағы ∆A₁ ' B₁ ' C₁ ' = ∆A₁ B₁ C₁ болады. Бір түзудің бойында табылатын жаңа А₂´, В₂´, С₂´ горизонталь проекцияларын саламыз. Жаңа α´ жағдайында α жазықтығы горизонталь проекциялаушы болды. Егер біз α жазықтығын фронталь проекциялаушы жағдайға келтіретін болсақ, оны π₂ жазықтығына қатысты жазық- параллель ығыстыру керек (1. 5-сурет) .

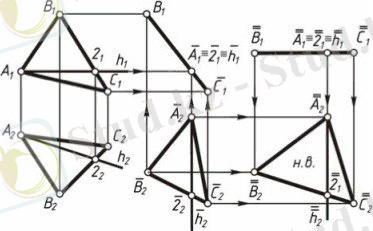
1. 5-сурет

4-есеп . Проекциялаушы жазықтықты деңгейлік жағдайға келтіру. Егер горизонталь проекциялаушы α´ жазықтығы берілсе, оны фронталь жағдайға келтіру үшін π2 жазықтығына қатысты жазық-параллель ығыстыру керек (1. 4-сурет) . Ол үшін алдымен көлденең түзу салып, оның бойына А₂″, В₂″, С₂″ нүктелерін А₂″В₂″= А₂´В₂´ және В₂″С₂″= В₂´С₂´ болатындай белгілейміз. А´₁, В´₁, С´₁ нүктелері арқылы көлденең түзулер жүргізіп, ал А₂″, В₂″, С₂″ нүктелері арқылы тік түзулер жүргіземіз. Аттас проекциялары арқылы жүргізілген түзулердің қиылысуында жаңа А₂″, В₂″, С₁″ фронталь проекцияларын табамыз. Егер фронталь проекциялаушы α жазықтығы берілсе, оны горизонталь жағдайға келтіру үшін π₁ жазықтығына қатысты жазық-параллель ығыстыру керек ( 1. 5-сурет) . Бұл есепті шығару нәтижесінде АВС үшбұрышының нақты шамасын анықтаймыз:

∆A₁′′ B₁ ′′ C₁ ′′ = ∆A₂ B₂C₂ = ∆ABC.

Проекциялаушы түзуден айналдыру тәсілі

Түрлендірудің инварианттары: нүктені проекциялар жазықтығына перпендикуляр осьтен айналдырғанда оның бір проекциясы шеңбер бойымен, ал екіншісі - айналдыру осіне перпендикуляр түзудің бойымен қозғалады. 1. 6-суретте А нүктесі сызатын шеңбер π₂ жазықтығына бұрмалаусыз нақты шамасына, ал π₁ жазықтығына түзу кесіндісі түрінде проекцияланады. Ал егер нүктені фронталь проекциялаушы осьтен айналдырсақ, нүкте траекториясы фронталь проекция жазықтығына шеңбер түрінде, ал горизонталь проекциялар жазықтығына оське перпендикуляр түзудің кесіндісі түрінде проекцияланады.

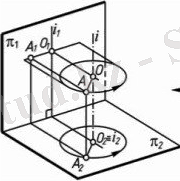1. 6-сурет

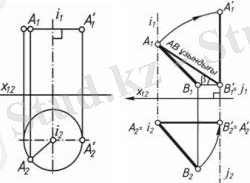
1. 7-сурет

1. 7-суретте жалпы жағдайдағы түзуді алдымен горизонталь проекциялаушы i осінен айналдырып, деңгейлік (фронталь) жағдайға келтірген. Содан соң фронталь проекциялаушы j осінен айналдырып, проекциялаушы жағдайға келтірген, яғни түзу π₂ жазықтығында нүктеге проекцияланады.

1. 3. Деңгейлік түзуден айналдыру тәсілі

Бұл тәсіл көбінесе жазық фигураның сызбасын түрлендіру үшін қолданылады. Жазық фигура дейгейлік жағдайға дейін айналдырылады және сәйкес жазықтыққа бұрмалаусыз проекцияланады.

Түрлендірудің инварианттары:

фигураның кез келген нүктесінің ескі және жаңа проекциялары айналдыру осіне перпендикуляр бір түзудің бойында орналасады;
фигураның кез келген кесіндісінің жаңа проекциясының ұзындығы оның нақты шамасына тең болады.

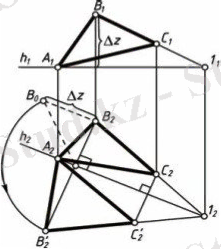
1. 8-сурет

1. 8-суретте АВС үшбұрышымен берілген жазықтықта А төбесі және 1 нүктесі арқылы горизонталь жүргізілген. Горизонтальді айналдыру осі ретінде қабылдаймыз. А және 1 нүктелері айналдыру кезінде қозғалыссыз болады. В және С нүктелері ось төңірегінде шеңбер бойымен қозғалады. Бұл шеңберлердің горизонталь проекциялары ось проекциясына перпендикуляр түзулер болады. Үшбұрыш горизонталь орналасу үшін, В төбесінің айналу радиусы өзінің нақты шамасына проекциялану керек. RВ радиусының ұзындығын тік бұрышты үшбұрыш тәсілімен анықтауға болады. В төбесінің айналу радиусының горизонталь жағдайдағы орнын анықтаған соң, С төбесінің айналу траекториясының проекциясы мен В´1 түзуінің қиылысында С' төбесін анықтаймыз. Табылған АВ´С´ проекциясы АВС үшбұрышының нақты шамасы болады.

1. 4. Проекциялар жазықтықтарын алмастыру тәсілі

Бұл тәсілде қарастырылып отырған фигура қозғалмайды да, проекциялар жазықтықтарының жүйесі жаңа өзара перпендикуляр проекциялар жазықтықтары жүйесімен алмастырылады (1. 9-сурет) . Жаңа проекциялар жазықтықтарының жүйесін берілген фигура дербес жағдайда болатындай етіп қабылдайды.

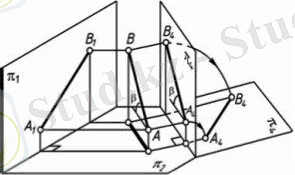
1. 9-сурет (а)

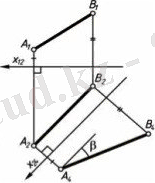
1. 9-сурет (ә)

Түрлендіру инварианттары : нүктенің жаңа проекциясынан жаңа оське дейінгі қашықтық оның ескі проекциясынан ескі оське дейінгі қашықтыққа тең.

Мысалы, АВ кесіндісінің нақты шамасын анықтау керек. Ол үшін АВ түзуін деңгей түзуіне түрлендіру керек. 1. 9, а, ә - суреттерінде жаңа ось АВ түзуінің горизонталь А₂В₂ проекциясына параллель, ал жаңа А₄ проекция жазықтығы АВ түзуіне параллель орналасқан. АВ түзуі А₄ проекция жазықтығына нақты шамасымен проекцияланады. Жаңа А₄ проекция жазықтығы мен х₂₄ осі түзуден кез келген қашықтықта орналасуына болады, оларды түзудің өзімен және оның проекциясымен беттестіріп қабылдаса да болады.

Қорытынды

Проекцияның түрі, оның формасы мен өлшемдері проекцияланушы фигурамен проекция жақығының өзара орналасу жағдайына байланысты. Оның үш түрлі жаздайы болады:

1 жаздайы: фигура проекция жазығына параллельде, перпендикуляр да емес; фигурамен оның проекциясының арасында еш сәйкестік болмайды;

2 жағдайы: фигура проекция жазығына перпендикуляр орналасса, оның проекциясы түзуге айналады;

3 жағдайы: фигура проекция жазығына параллель орналасса, оның проекциясы фигураның өзіне тең.