Позициялық және метрикалық

Пән: Математика, Геометрия
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 16 бет
Таңдаулыға:

Позициялық және метрикалық

Жоспары

Кіріспе . . . 3

1. 1. Позициялық есептер . . . 4

1. 1. 1. Нүкте мен түзу сзықтың өзара орналасуы . . . 4

1. 1. 2. Түзу сызықтардың өзара орналасуы . . . 5
1. 1. 3. Екі жазықтықтың өзара орналасуы . . . 8
1. 1. 4. Түзу мен жазықтықтың өзара орналасулары . . . 9

1. 2. Метрикалық есептер . . . 12

1. 2. 1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы . . . 12

1. 2. 2 Нүкте мен жазықтықтың арақашықтығы . . . 13

Қорытынды . . . 16

Қолданылған әдебиеттер . . . 17

Кіріспе

Метрикалық есеп деп өлшемдерді анықтаумен байланысты есептерді айтамыз. Метрикалық есептерде арақашықтық, бұрыштың шамасы, геометриялық фигуралардың аудандарының натурал шамалары анықталады. Метрикалық есептерді шешу үшін өзара перпендикуляр түзулер мен жазықтықтарды салуға тура келеді.

Өзара перпендикуляр екі түзудің біреуі горизонталь болса, олардың горизонталь проекциялары өзара перпендикуляр болады.

Өзара перпендикуляр екі түзудің біреуі фронталь болса, олардың фронталь проекциялары өзара перпендикуляр болады.

Өзара перпендикуляр екі түзудің біреуі профиль түзуі болса, олардың профиль проекциялары өзара перпендикуляр болады.

Түзу жазықтыққа перпендикуляр болуы үшін сызбада оның горизонталь проекциясы жазықтықтың горизонталінің горизонталь проекциясына, ал фронталь проекциясы жазықтықтың фронталінің фронталь проекциясына перпендикуляр болуы қажет және жеткілікті.

Екі түзудің біреуі арқылы екіншісіне перпендикуляр жазықтық жүргізуге мүмкіндік болса, олар өзара перпендикуляр болады.

Жалпы жағдайдағы түзуі кесіндісінің ортогональ проекциялары әрқашан кесіндінің өзінің ұзындығынан кем болады.

Позициялық (тұрғылықты) жəне метрикалық (өлшем) есептер жалпы сызба геометрияның негізгі есептері болып табылады. Позициялық (тұрғылықты) есептер дегеніміз - геометриялық фигуралардың сызбалары арқылы олардың кеңістіктегі өзара орналасуын анықтайтын есептер. Позициялық есептерге: нүкте мен түзудің, түзу мен түзудің, нүкте мен жазықтықтың, түзу мен жазықтықтың, жазықтық пен жазықтықтықтың, жазықтық пен беттің, екі беттің өзара орналасу есептері жатады.

Метрикалық (өлшем) есептер дегеніміз - геометриялық фигуралардың сызбалары арқылы олардың кеңістіктегі өзара қашықтықтарын, олардың арасындағы бұрышын жəне олардың ауданын, нақты шамасын т. с. с. жағдайын анықтайтын есептер.

Позициялық есептер

Күрделі емес позициялық есептерді шешуде көбінесе жалпы əдістер пайдаланылады. Бұл параграфта кеңістіктегі нүкте мен түзу сызықтың өзара орналасуы, кеңістіктегі түзу сызықтардың өзара орналасуы, кеңістіктегі екі жазықтықтың өзара орналасуы жəне кеңістіктегі түзу мен жазықтықтың өзара орналасулары сияқты позициялық есептерді қарастырамыз.

4. 1. 1 Нүкте мен түзу сызықтың өзара орналасулары

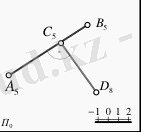
Кеңістікте нүкте мен түзу сызық əртүрлі жағдайда кездесуі мүмкін. Кеңістікте нүкте түзу сызық бойында немесе түзу сызықтан тыс орналасуы мүмкін. Осы тақырыпқа мысал ретінде 1-суреттегі нүктелер мен түзудің өзара орналасуларын қарастырайық. 1-суреттегі С5 нүктесі - А5 В2 түзу сызығынан тыс жатқан нүкте. Ал, D3 нүктесі - А5 В2 түзу сызығының бойында жатқан нүкте, өйткені бұл нүкте түзу сызықтың ен аралыққа бөлгендегі үшінші бөлігіне тең.

Үшінші Е7 нүктесін алсақ, бұл нүкте проекциясы түзу сызық бойында жат- қанымен, түзу сызықтан тыс орналасқан, түзу бойында жатпайтын нүкте. Себебі, Е7 нүктесі түзу сызық бойында жатпайды, 4-енаралық үстінде орналасқанымен, бұл нүктенің сандық белгісі 7-ге тең.

1-сурет

1. 1. 2 Түзу сызықтардың өзара орналасуы

Түзу сызықтар кеңістікте өзара орналасуларына байланысты: параллель, қиылысқан, айқасқан жəне перпендикуляр (тікше) болып келеді.

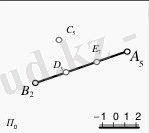
Егер кеңістіктегі екі түзу сызықтың көл денең П0 проекция жазықтығындағы кескіндерінің кескін табандары өзара параллель, ен аралықтары тең жəне сан- дық белгілері бір бағытта өсетін болса, онда мұндай түзу сызықтарды өзара парал лель түзулер дейді. Мысал ретінде 2-cуретте орналасқан А5 В2 жəне С5 D8 түзу сызық тарын қарастырайық. Көлденең П0 жазық- тығында кескінделген А5 В2 түзуіне С5 D8 түзу сызығы параллель орналасқан, өйткені екі түзу сызықтың кескіндері өзара параллель, ен аралықтары тең жəне өсу бағыттары сəйкес келген түзулер.

Егер екі түзудің кескін табандары бір нүк- теде қиылысса жəне осы нүктедегі сандық белгілері бірдей болса, ондай түзулер өзара қиылысқан түзулер деп аталады (38-сурет) . Мысал қарастырайық. Көлденең П0 жазық- тығында өзара қиылысқан А9 В4 түзу сызығы мен С5 D8 түзу сызығының кескіні берілген жəне екі түзу К6 нүктесінде қиылысады. Берілген екі түзу сызықты ен аралықтарға бөлеміз. Бөлінген ен аралықтар алтыншы санында қиылысып жатыр. Демек, бұл екі түзу сызық - өзара қиылысып жатқан түзу сызықтар.

2-сурет

3-сурет

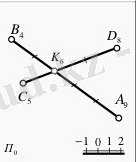
Егер кеңістіктегі екі түзу кескін табандары қиылысқан болса, бірақ ортақ қиылысу нүктесі болмаса жəне түзулердің ен аралықтары əртүр- лі болса, онда мұндай түзулер өзара айқас түзулер деп аталады. Мысал ретінде 4-cуретте орналасқан түзу сызықтарды қарастырайық. Көлденең П0 жазықтығында кескінделген өзара қиылысып жатқан А7 В2 түзуі мен С5 D8 түзу сызықтары берілген. Бұл қиылысып жатқан түзулердің ортақ нүктесі жоқ. Түзулердің ен аралықтары өзара тең емес, яғни бұл түзулер айқасып жатыр. Өзара айқас түзулердің кейде кеңістіктегі кескін табандары өзара параллель болып та келеді, бірақ өсу бағыттары қарама-қайшы болады.

4-сурет

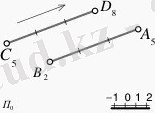
Өзара айқасып жатқан түзулерге тағы бір мысал ретінде 5-cуретті қарастырайық. П0 жазықтығында кескінделген А9 В5 түзуі мен С5 D8 түзу сызықтары берілген. Бұл қиылысып жатқан түзулердің ортақ нүктесі жоқ. Түзулердің ен аралықтары өзара тең емес, яғни бұл түзулер айқасып жатыр.

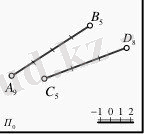
5-сурет

Егер кеңістіктегі орналасқан түзу сы- зықтардың кескін табандары қиылысқан, бірақ түзу сызықтың біреуінің кесінді табаны горизонталь (деңгейлік) түзу болса, ал екінші түзу сызық осы түзу сызыққа (кескін табаны) перпендикуляр орналасса, онда мұндай түзулер өзара перпендикуляр түзулер деп аталады (6-сурет) . Өзара перпендикуляр түзулерге мы- сал ретінде 6-cуретті қарастырайық. 6-cуретте көлденең П0 жазықтығына параллель орналасқан А5 В5 түзуі берілген. Осы түзу сызықтың бойында жатқан С5 нүктесін белгілеп алып, С5 нүктесі арқылы перпендикуляр С5 D8 түзу сызығын жүргіз- сек, онда бұл түзулер өзара перпендикуляр түзулер болады.

6-сурет

1. 1. 3 Екі жазықтықтың өзара орналасуы

Жазықтықтар да түзу сызықтар сияқты өзара параллель жəне қиылысқан болып келеді.

Егер кеңістікте орналасқан екі жазықтықтардың көлбеу масштабы арқылы берілген проекциялары өзара параллель, ен аралықтары тең жəне сандық белгілері бір бағытта өссе (немесе төмендесе), онда мұндай жазықтықтарды өзара параллель жазықтықтар деп атайды.

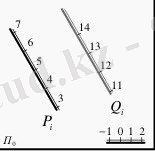
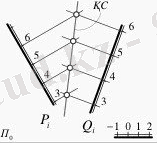
7-суретте Р жəне Q жазықтықтарының көлбеу масштабы арқылы берілген кескіндері көрсетілген. Суретте көрсетілгендей екі жазықтықтардың ен аралықтары мен өсу бағыттары өзара тең. Көлбеу масштабы арқылы берілген жазықтықтардың кескіндері де өзара параллель орналасқан. Егер жоғарыдағы айтылған қағидалар орындалмаса, яғни ен аралықтары мен өсу бағыттары өзара параллель орналаспаған болса, онда мұндай жазықтықтарды өзара қиылысқан жазықтықтар деп атайды (8-сурет) . Жоғарыдағы мысалдағыдай, 8-суретте Р жəне Q жазықтықтарының көлбеу масштабы арқылы берілген кескіні көрсетілген. Жазықтықтардың ен аралық- тары əртүрлі жəне жазықтықтардың кескіндері өзара параллель емес, яғни кеңістікте орналасқан екі жазықтық ортақ қиылысу сызығында қиылысады. Енді осы қиылысу сызығын анықтау үшін, жазықтықтардың ен аралықтарынан жазықтық кескініне перпендикуляр болатындай сəулелер жүргіземіз. Екі жазықтықтан жүргізген өзара аттас сəулелерді өзара қиылысқанға дейін созамыз. Егер осы табылған қиылысу нүктелерін өзара қоссақ, онда табылған сызық екі жазықтықтың қиылысу сызығы болады (8-сурет) .

7-сурет 8-сурет

1. 1. 4 Түзу мен жазықтықтың өзара орналасулары

Кеңістікте түзу сызықтар жазықтыққа параллель, меншікті (жазықтық бойында жатады) жəне перпендикуляр (тікше) қиылысады. Енді осы жағдайларға мысал қарастырамыз.

Егер түзудің екі нүктесі жазықтық бойында жатса, онда мұндай түзу сызық жазықтыққа меншікті болады. Мысал қарастырайық. 9-суретте Р жазықтығының көлбеу масштабы арқылы берілген кескіні көрсетілген. Түзудің А жəне В нүктелері осы жазықтықтың аттас горизонтальдарының бойында жатыр, яғни АВ түзу сызығы Р жазықтығына меншікті болады.

9-сурет

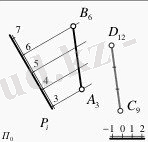Егер жазықтыққа меншікті түзу сызыққа екінші бір түзу параллель болса, онда бұл түзу сызық жазықтыққа параллель болады. Мысал ретінде 10-cуретті қарастырайық. Суретте көлбеу масштабы арқылы берілген Р жазықтығы мен осы жазықтыққа меншікті АВ түзуі берілген. АВ түзуінің А жəне В нүктелері Р жазықтығының аттас горизонтальдар бойында жатыр. АВ түзу сызығына параллель болатын СD түзуін жүргіземіз. Егер СD түзу сызығы АВ түзуіне параллель болса, онда СD түзу сызығы Р жазықтығына да параллель болғаны.

10-сурет

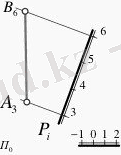
Егер түзу сызық жазықтыққа меншіксіз немесе жазықтыққа параллель болмаса, онда мұндай түзу сызықтар жазықтықпен қиылысады (11-сурет) .

Жазықтықпен түзу сызықтың қиылысу нүктесін табу үшін, 11-суретте көрсетілгендей, А3 В6 түзу сызығы арқылы кез келген проекцияланушы Q жазықтығын жүргіземіз. Бұл Q жазық- тығын жүргізіп отырған себебіміз - екі жазықтықтың қиылысу сызығын анықтау. Ол үшін жазықтықтарды ен аралықтарға бөліп, осы ен аралықтардан горизонталь түзулерін жүргіземіз. Аттас горизонтальдар өзара қиылысып, екі жазықтықтың қиылысу сызығын анықтаймыз. Енді осы табылған қиылысу сызығын берілген А3 В6 түзу сызығына дейін созып, К7 қиылысу нүктесін табамыз (11-cурет) .

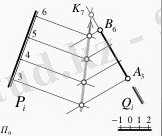
11-сурет

Егер түзу сызықтың проекциясы көлбеулік масштабы арқылы берілген жазық тыққа параллель (немесе жазық- тықтың горизонталына перпендикуляр), ен ара лықтары кері пропорционал болса жəне ен аралықтарының сандық белгілері кері қарай өссе, онда мұндай түзу сызықтарды жазықтыққа перпендикуляр орналасқан түзу сызықтар дейді (12-cурет) .

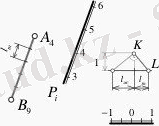
12-сурет

Жазықтыққа перпендикуляр түзу жүргізу үшін, алдымен көлбеулік масштабы арқылы берілген Р жазықтығы мен осы жазықтыққа меншікті А4 нүктесі берілсін. Осы берілген меншікті нүкте арқылы перпендикуляр түзу сызық жүргізу үшін түзудің ен аралығын анықтау қажет. Ол үшін тікбұрышты үшбұрыштар əдісін пайдаланамыз. Түзу сызық бойына жазықтықтың ен аралығын l ж өлшеп салып, 12-суретте көрсетілгендей, масштаб сызғышынан бір бірлікті өлшеп алып, жазықтықтың ен аралығы l ж сызылған сызыққа перпендикуляр түсіріп, К нүктесін табамыз. Осы нүкте арқылы тікбұрышты үшбұрышты саламыз. Табылған үшбұрыштың гипотенузасын К нүктесінен жүргізілген сызық (қызыл сызық) L нүктесінде қиып өтеді. Осы нүкте мен жазықтық (l ж) ен аралығының арақашықтығы түзу сызықтың ен аралығы l т болады. Енді А4 нүктесінен көлбеулік масштабы арқылы берілген Р жазықтығына параллель түзу жүргізіп, осы түзу бойына түзу сызықтың ен аралығын - l т өлшеп саламыз. Бұл табылған түзу сызық жазықтыққа перпендикуляр түзу болып табылады.

1. 2 Метрикалық есептер

Сандық белгісі бар проекциялар горизонталь П0 жазықтығында орындалса да, сызбада тікбұрышты (ортогональ) проекциялар қағидаларымен құрылатын болғандықтан, тікбұрышты проекцияларда қолданылатын əдістердің көбін сандық белгісі бар проекцияларда да пайдалануға болатынын айта кету керек. Сондықтан метрикалық (өлшем) есептерді шешуде жалпы əдістерді пайдаланамыз.

1. 2. 1 Түзу сызықтың нақты шамасы мен жазықтыққа жасайтын бұрышы

Егер түзу сызық кеңістікте жалпы жағ дайда орналасқан болса, онда оның көлденең П0 жа- зық тығындағы проекциясы бұрмаланып, түзу сызық ұзын немесе қысқа болып кескінделеді.

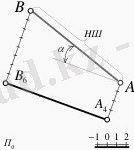
Сандық белгісі бар проекцияларда жалпы жағдайда берілген түзу сызықтың нақты шама сын (ұзындығын) табу үшін, берілген А4 В6 түзуінің А4 жəне В6 нүктелерінен түзуге перпендикуляр сызық жүргіземіз. Осы сызық бойына сан өлшемдерін өлшеп саламыз. Егер табылған А жəне В нүктелерін өзара қоссақ, онда жүргізілген түзу сызық ұзындығы түзудің нақты шамасы болады (13-сурет) .

Енді түзудің жазықтыққа жасайтын бұры шын анықтау үшін, А нүктесінен А4 В6 түзуінің сандық белгісі бар проекциясына параллель түзу жүргіземіз. Осы түзу мен түзудің нақты шамасының арасындағы бұрышы А4 В6 түзу сызығы мен көлденең П0 жазықтықтың арасындағы бұрышы болып табылады.

13-сурет

1. 2. 2 Нүкте мен жазықтықтың арақашықтығы

Жоғарыда айтып кеткендей, метрикалық есептер деп гео метриялық фигуралардың сыз бал ары арқылы олар дың кеңіс тік тегі өзара қашық тықтарын аны қтайтын есептерді айтады.

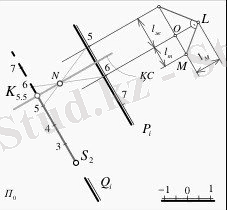
Нүкте мен жазықтықтың ара қашықтығын анықтауға мы сал ретінде 14-суретті қа рас тырайық. Суретте кеңіс тік те орналасқан S2 нүктесі мен көлбеулік масштабы ар қылы Р жазықтығы берілген. Жазықтыққа S2 нүктесі ар қылы перпендикуляр түзу сызық жүргіземіз. Бұл түзу сызықтың ен аралығын анықтау үшін, тікбұрышты үшбұрыш əдісін пай даланамыз. Сызық бойына жазықтықтың ен аралығын l ж өлшеп, О нүктесін анықтаймыз. Осы сызыққа перпендикуляр масштаб сызғышынан бір бірлікті өлшеп салып, L нүктесін табамыз. Табылған көлбеу сызыққа (жасыл сызық) перпендикуляр (қызыл) сызық жүргіземіз. Бұл қызыл сызық бастапқы жүргізілген сызықты М нүктесінде қиып өтеді. М жəне О нүктелерінің арақашықтық перпендикуляр түзу сызығының ен аралығы l т болады. Осы табылған ен аралықты S2 нүктесінен көлбеулік масштабы арқылы берілген Р жазықтығына жүргізілген параллель түзу сызық бойына өлшеп саламыз.

14-сурет

Енді осы түзу сызықтың жазықтықпен қиылысу сызығын анықтау керек. Ол үшін түзу арқылы проекцияланушы Q жазық- тығын жүргіземіз. Осы Q жазықтығы мен көл- беулік масштабы арқылы берілген Р жазықтығының қиылысу сызығын анық- таймыз. Осы қиылысу үшін, екі жазықтықтың аттас горизонтальдарын өзара қосамыз. Барлық өзара қосқан аттас горизонтальдар тек қана бір түзуде қиылысады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.