Алгебра және анализ бастамаларын оқыту барысында математикалық анализдiң негiзгi ұғымдарын есептердi пайдаланып қалыптастыру

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

КІРІСПЕ

Зерттеу тақырыбының көкейкестiлiгi . Қазақстан Республикасының Президенті Н. Ә. Назарбаевтың Қазақстан халқына Жолдауында білім беру реформасы - Қазақстанның бәсекеге нақтылы қабілеттілігін қамтамасыз етуге мүмкіндік беретін аса маңызды құралдардың бірі делінген.

Осыған орай жалпы бiлiм беретiн мектептің көкейкестi проблемаларының бiрi оқыту үдерісі кезiнде оқушылардың танымдық белсендiлiлiгiн, болашақтағы оқу іс-әрекетi үшiн сапалы дайындығын арттыру болып табылады. Оқушылардың танымдық іс-әрекетін белсендiруде есептiң рөлi жоғары, есеп шығару барысында оқушылардың негiзгi математикалық бiлiм, бiлiктілік, дағдылары қалыптасады. Әйгiлi поляк әдіскер-математигi А. С. Крыговская сөзiмен айтсақ, «есеп арқылы оқыту принципi математиканың өзiндiк табиғи салдары».

Есеп арқылы оқыту әдiсi өте ертеден белгiлi болған. Ежелгi грек философы Сократ оқыту барысында есептiң шешiмi арқылы қорытынды жасауға болатындай есептер жиынтығын пайдаланған. Оқушылардың даму мүмкiндiгi тек өзiндiк жұмыстың барысында ғана қалыптасады деген пікір көптеген белгiлi педагогтардың ойларынан шыққан. А. Дистервег оқушылар ұғымды өзбетімен есептерi шығару барысында ашу керек деген.

Есеп шығару барысында оқушылар тек математика курсын белсендi игеріп қана қоймай, олар шығармашылық ойлау икемдiлiгiн меңгереді. Саналы құрылған есептер арқылы оқушылардың есептердi шығарудың тәсiлдерiн білудегі, шешiмдерiн жалпылаудағы, теориялық заңдылықтарды ашудағы ойлау іс-әрекетiн бiр жүйеге келтіреді.

Есеп арқылы оқытуда С. И. Шoхор-Троцкий, Д. Пойа, П. М. Эрдниев, А. М. Фридман, Ж. Икрамов, А. С. Крыговская, Ю. М. Колягин, Я. И. Груденов, отандық педагог математиктерi Б. Баймұханов, Е. У. Медеуов, Д. Рахымбек, С. Е. Шәкілікова және тағы басқалардың зерттеу жұмыстарының нәтижелерi үлкен үлес болып табылады.

Жоғары сыныптардағы алгебра және анализ бастамалары материалдарының абстракциялығынан есептер арқылы оқытудың қажеттілігі артты. Математикалық анализ ұғымдарын оқушыға түсінікті және оның ішкі мазмұнын ашатын оқыту әдісі - есеп арқылы оқыту болса, онда бұл бөлімді оқыту әдістемесіне оқушыларға түсінікті логикалық және интуитивтік аспекті енгізу керек. Кеңес дәуірінде математиканы мектепте оқытуда интуицияның рөлі және оқушы интуициясын пайдалану туралы мәселелермен П. С. Александров, А. А. Ляпунов, Л. Д. Кудрявцев, В. Л. Гончаров, А. А. Столяр, Н. В. Метельский, П. М. Эрдниев және т. б. айланысты. Интуиция психологиялық-педагогикалық әдебиеттерде «Ақиқатты дәлелдеменің көмегіне негіздемей өз көзқарасымен түсінуге қабілеттілік» делінген. Математикалық анализді есептер арқылы оқыту есептің ішкі мазмұнын меңгеруден, есепті түсінудегі логикалық қадамдардан, алынған қортындылар мен бақылау нәтижелерінен шығады.

Математикалық анализдің негізгі ұғымдары шек, шекке көшу, үзіліссіздік, функцияның нүктедегі шегі, туынды, интеграл ұғымдарының жоғары деңгейдегі абстракциялылығы, олардың анықтамасының күрделі логикалық құрылымы, оқу уақытының жеткіліксіздігі және т. б оқыту үдерісіне бірқатар қиындықтар туғызды. Математикалық анализдің негізгі ұғымдарын енгізудің тиімді әдістерін іздестіру бағытында зерттеу жұмыстары өте қажет.

Алгебра және анализ бастамаларын оқытудың сапалы құралы - математикалық анализдiң мазмұнын айқындайтын таңдамалы есептер. Есептер арқылы оқытуға байланысты көптеген жұмыстар жасалғанына қарамастан әлi де бұл проблема толық зерттелмеген: есептер арқылы оқытудың негiзгi заңдылықтары, математикалық анализді есептер арқылы оқыту мүмкiндiгi толық анықталып, есеп арқылы оқытудың нақты әдiстемесi дайындалмаған. Орта мектепте математикалық анализдің негізгі ұғымдарын есеп арқылы оқыту практикасы мынаны: а) математикалық теорияны оқытуда есептерді пайдаланудың стихиялық сипатын; б) математика пән мұғалімдерінде математикалық анализдің негізгі ұғымдарын есеп арқылы оқытуға қажетті тәжірибе жұмыстарының жеткіліксіздігін көрсетті.

Ю. М. Колягиннің теориялық және эксперименттік зертеулерінде көрсетілгендей орта мектепте математикалық анализді оқыту практикасында есептердi пайдаланудың әдiстемесі әлі күнге дейін жасалмаған. Мұндай жағдайда орта мектепте математикалық анализдiң негiзгi ұғымдарын есеп арқылы қалыптастыру қажеттiлiгi мен оны ғылыми-әдістемелік жағынан негіздеудің жеткіліксіздігі арасында қарама-қайшылықтар туындады. Орта мектепте математикалық анализдiң негiзгi ұғымдарын қалыптастыруда есептердi қолданудың әдістемелік жүйесін дайындаудың көкейкестiлiгi зерттеу тақырыбын «Орта мектепте математикалық анализдiң негiзгi ұғымдарын қалыптастыруда есептердi пайдалану әдiстемесi» деп атауға негіз болды.

Зерттеу мақсаты: алгебра және анализ бастамаларын оқыту барысында математикалық анализдiң негiзгi ұғымдарын есептердi пайдаланып қалыптастыруды теориялық тұрғыда негіздеп, оны жүзеге асырудың әдістемесін жасау.

Зерттеу нысаны : орта мектепте математикалық анализдің элементтерін оқыту үдерiсi.

Зерттеу пәнi : алгебра және анализ бастамаларын оқыту барысында математикалық анализдiң негiзгi ұғымдарын есептердi пайдалану арқылы қалыптастыру.

Зертеудің ғылыми болжамы: егер, орта мектепте алгебра және анализ бастамаларын оқыту барысында теориялық материалдардың мағынасын ашатын есептер белгілі бір жүйемен орналастырылып, есеп арқылы оқыту әдістемесі енгізілсе, онда математикалық анализдiң негiзгi ұғымдары саналы түрде қалыптасады, өйткені есептер арқылы оқыту оқушылардың танымдық белсенділігін арттырып, шығармашылық ойлауын дамытады.

Зерттеу жұмысының мақсаты мен болжамына сәйкес мынадай мiндеттердi шешу қажет болды:

- математикалық ұғымдарды есеп арқылы қалыптастырудың теориялық және практикалық жағдайын талдап, оқыту үдерісінде есептi қолданудың психология-дидактикалық аспектiлерiн негiздеу;

- орта мектепте математикалық анализдің негізгі ұғымдарын есептерді қолдану арқылы алдын ала дайындаудың қажеттілігі мен мүмкіндігін айқындау;

- орта мектепте математикалық анализдiң негiзгi ұғымдарын есептердi пайдаланып қалыптастырудың әдiстемесiн дайындау және оған экспериментiк тексеріс жасау.

Зерттеудiң жетекші идеясы: математикалық анализдің негізгі ұғымдарын есеп арқылы оқыту барысында оқушылардың танымдық белсенділігін жанама басқара отырып, өздігінен білім алуға даярлау - жеке тұлға қалыптастырудың құрамдас бөлігі болып табылады.

Зерттеудiң әдiснамалық және теориялық негiзi: таным, білім, жеке тұлға және оның танымдық іс-әрекеті, ақыл-ой белсенділігі, адами құндылықтары туралы философиялық, психология-педагогикалық, дидактикалық, теориялар мен тұжырымдамалар. Зерттеу әдіснамасын дайындауда ақыл-ой әрекетiн сатылап қалыптастыру және дамыта оқыту теориясы басшылыққа алынды.

Зерттеу көздерi: Қазақстан Республикасының Конституциясы, «Білiм туралы» Заңы, Қазақстан Республикасының 2015 жылға дейінгі бiлiм беру жүйесiн дамыту тұжырымдамасы, Қазақстан Республикасының жалпы орта білім берудің мемлекеттік жалпыға міндетті стандарты, педагогтар мен психологтардың еңбектерi, математикалық анализді оқытуда есептердi пайдаланатын орта мектеп мұғалiмдерiнiң озық іс-тәжiрибелерi, автордың өзiнiң педагогикалық тәжiрибесi болып табылады.

Зерттеу әдiстерi: зерттеу проблемасына сәйкес философиялық, психология-педагогикалық, ғылыми-әдiстемелiк әдебиеттерге және орта мектептегі алгебра және анализ бастамаларының мазмұнына талдау жасау; орта мектепте математикалық анализдi оқыту тәжiрибелерiн және оқушылардың оқу іс-әрекеттерiн, сонымен бірге олардың нәтижелерiн талдау; айқындау, iздену, оқыту эксперименттерiн ұйымдастыру және жүргiзу; олардың сандық және сапалық нәтижелерiне өңдеу жасау.

Зерттеудің ғылыми жаңалығы мен теориялық маңызы :

- математикалық анализдің негiзгi ұғымдарын есептерді пайдаланып қалыптастырудың тұжырымдамасы теориялық тұрғыда негiзделді;

- математикалық анализдің негізгі ұғымдарын есептер арқылы қалыптастыру деңгейі және математикалық анализ бастамаларын оқытуда алдын ала дайындықтың мүмкіндігі мен қажеттілігі анықталды;

- жоғары сыныптарда алгебра және анализ бастамаларын есеп арқылы оқытудың әдiстемесi әзірленді.

Зерттеудiң практикалық мәнділігі: Алгебра және анализ бастамаларын есеп арқылы оқытуға арналып әзірленген әдiстемені мұғалiмдер оқушылардың бiлiм сапасын көтеруде, олардың танымдық іс-әрекетiндегі белсендiлігін арттыруда қолданады. Жаңа буынға оқулықтар дайындауда оқулықтар мен оқу құралының авторы пайдалана алады.

Қорғауға ұсынылатын негізгі қағидалар :

- орта мектепте математикалық анализдің негізгі ұғымдарын қалыптастыруда есептерді қолданудың психология-дидактикалық алғы шаттары;

- орта мектепте математикалық анализдің негізгі ұғымдарын есептерді қолданып қалыптастыруда алдын ала дайындаудың рөлі мен атқаратын қызметі;

- орта мектепте математикалық анализдің негізгі ұғымдарын есептер жүйесін қолдану арқылы қалыптастыру әдістемесі.

Зерттеудiң негiзгi кезеңдерi . Диссертация тақырыбына сәйкес зерттелетiн проблема бiрнеше жылда жүзеге асырылды, зерттеу өзара логикалық байланысты үш кезеңге бөлiндi.

Бiрiншi кезеңде (2000-2002. ) диссертация тақырыбына сәйкес зерттелетiн мәселе бойынша психология-педагогикалық және әдiстемелiк әдебиеттерді оқып-үйрену, жоғары оқу орнының оқытушылары мен мектеп мұғалiмдерiнің озық іс-тәжiрибелерi жинақталып, талдау жасалды. Зерттеу тақырыбы бойынша математикалық анализдің негiзгi ұғымдарын оқытуда есептердi қолданудың формасы мен әдiсi анықталды. Мектеп мұғалiмдерімен, студенттермен, жоғары оқу орнының оқытушыларымен әңгiмелесу, сауалнама, бақылау жүргiзілді, соның негізінде проблема нақтыланды, теориялық-эксперименттiң алғы шарттары айқындалды. Бұл кезеңде зерттеудiң ғылыми-әдістемелік негiздемесі және ғылыми аппараттары анықталып, жоспары құрылды.

Екiншi кезеңде (2003-2004) математикалық анализдің негізгі ұғымдарын қалыптастыру үшін алдын ала есеп арқылы дайындаудың мүмкіндіктері анықталып, арнайы әзірленген есептер жүйесіне қойылатын талаптар айқындалды. Зерттеудiң бұл кезеңінде эксперименттiк сыныптарда оқушылардың өзiндiк оқу іс-әрекеттерiн ұйымдастыру шаралары бақыланды. Орта мектепте алгебра және анализ бастамаларының негiзгi ұғымдарын қалыптастыруда есептердi қолданып оқыту эксперименті жүзеге асырылды.

Үшiншi кезеңде (2005-2006) жүргiзiлген педагогикалық экспериментке өңдеу жасалып, оның нәтижесi зерттеу болжамымен салыстырылды, жалпылама қорытынды жасалды. Алынған нәтижелер математикалық статистика мен экспертiк бағалаудан өтті. Зерттеу нәтижесi диссертация түрiнде өрнектелді

Зерттеу нәтижелерінің дәйектілігі мен сенімділігі: зерттеу проблемасы бойынша психологиялық-педагогикалық, оқу-әдістемелік әдебиеттер мен оқу құралдарына, алгебра және анализ бастамаларын оқытудың жайын жан-жақты терең талдай отырып, зерттеу жасалынып, олардың негізге алынуы; зерттеу міндеті мен логикасына сай зерттеу тәсілдерін пайдалану; теориялық талдау мен педагогикалық эксперименттің өзара байланыстылығы, эксперименттік тәжірибе жұмысының нәтижелеріне сапалық және сандық талдау жасалынып, нәтижелері математикалық статистика тәсілдерімен өңдеу арқылы қамтамасыз етілуі.

Зерттеу базасы. I. Жансүгiров атындағы Жетiсу мемлекеттiк университетiнiң математика және информатиканы оқытудың әдістемесі кафедрасында, Талдықорған қаласындағы М. Арын атындағы №24 «Экономика және бизнес» лицейiнде, №18, №19, №4, Еркін ауылындағы №11, Өтенай ауылындағы №21 қазақ орта мектептерінде, Алматы облыстық мұғалiмдер бiлiмiн жетiлдiру институтында жүзеге асырылды.

Зерттеу нәтижелерін сынақтан өткізу және енгізу: зерттеу нәтижелері жалпы білім беретін мектептердің жоғары сынып мұғалімдеріне арналған әдістемелік нұсқау, мақала түрінде оқыту практикасына енгізілді.

І. Жансүгіров атындағы Жетісу мемлекеттік университетінде (Талдықорған, 2002, 2007), Семей мемлекеттік педагогикалық университетінде (Семей, 2009), Шымкент әлеуметтік-педагогикалық университетінде (Шымкент, 2009) өткен ғылыми-практикалық конференцияларында баяндамалар жасалып, талқыланды. Алматы обылыстық педагогикалық оқуларда, І. Жансүгіров атындағы Жетісу мемлекеттік университетінің математика және информатиканы оқыту әдістемесі кафедрасының семинарларында баяндамалар жасалды.

Зерттеу нәтижелері автордың 11 еңбектерінде көрініс тапты: оның ішінде Қазақстан Республикасының Білім және ғылым министрлігінің білім және ғылым саласын бақылау жөніндегі комитет алқасы ұсынған баспаларда: «Қазақстан мектебі» (Алматы, 2004), «Қазақстан мектебі» (Алматы, 2004), «Қазақстан мектебі» (Алматы, 2007), «Ұлт тағылымы» (Алматы, 2005) 4 мақала, халықаралық ғылыми-практикалық конференциялар материалдарының жинақтарында 3 мақала, республикалық ғылыми-практикалық конференциялар материалдарының жинақтарында 1 мақала, республикалық ғылыми-әдістемелік журналында 3 мақала жарияланды.

Диссертацияның құрылымы . Диссертация кiрiспеден, екi бөлімнен, қорытындыдан, пайдаланған әдебиеттер тiзiмi мен қосымшадан тұрады.

Кіріспеде зерттеу тақырыбының көкейкестілігі, зерттеу мақсаты, зерттеу нысаны, зерттеу пәні анықталды, зерттеу болжамы тұжырымдалды, зерттеу міндеттері мен ғылыми жаңалығы нақтыланды.

« Орта мектепте математикалық анализдің негізгі ұғымдарын есептерді пайдаланып қалыптастырудың психология-дидактикалық негіздері » деп аталатын бірінші бөлімде орта мектепте математикалық анализдің негізгі ұғымдарын есептерді қолдану арқылы қалыптастырудың психология-дидактикалық мәні ашылды, математиалық анализдің негізгі ұғымдарын қалыптастырудағы есептердің рөлі мен функциясы негізделді, интуиция мен шындыққа ұқсас талдаудың рөлі анықталды. Математикалық анализдің негізгі ұғымдарын қалыптастыруға есептер арқылы алдын ала дайындауды жүзеге асыру мүмкіндігі айқындалды.

« Математикалық анализдiң негiзгi ұғымдарын есептердi қолдану негiзiнде қалыптастырудың әдiстемесi» деп аталатын екінші бөлімде математикалық анализдің негізгі ұғымдарын есептер арқылы қалыптастыру деңгейі және математикалық анализ бастамаларын оқытуда алдын ала дайындықтың рөлi мен атқаратын қызметі анықталды. Математикалық анализдiң негiзгi ұғымдарын есептердi қолдану негiзiнде қалыптастырудың әдiстемесi жасалып, эксперименттік-тәжірибе жүзінде тексерілді.

Қорытындыда теориялық зерттеулер мен эксперименттік-тәжірибе жұмыстарының қорытындысы бойынша тұжырымдамалар жасалды және осы мәселені ары қарай зерттеудің болашағы бағдарланды.

Қосымшада оқу материалына келтіріліп өңделген есептер жүйесі мен алдын ала оқыту тапсырмалары қарастырылған.

НЕГІЗГІ БӨЛІМ

Психологиялық әдебиеттерде ойлау іс-әрекеттерін ұйымдастыруда есептің орнының ерекше екендігі жөнінде көп айтылған. Есептiң ойлау іс-әрекетiндегi мәнін аша отырып, А. Ф. Эсаулов есептiң психологиялық аспектiсi, есепті шығарушыға оның барлық жеке позициясы мен осыған сәйкес қатынасы сипатында қажетті ойлау туғыза алатын шарттар мен мақсаттарды ұйымдастырушы рөлінде көрінетінін айтқан. Есептiң қойылымы, есептi шығару адамның барлық сатылы-өспелi ой белсендiлiгiн, саналылығын, мақсатты ұмтылысын қамтамасыз етедi. Есептi психологияның категориясы деп қарастырған Г. С. Костюк, Г. А. Балл оқу іс-әрекетiн жетілдіру және оның тиімділігін арттыруда есепті пайдаланудың мүмкіндігін көрсете отырып, есептерді тек зерттеу жұмыстарында ғана емес, сонымен қатар оқыту үдерісін ұйымдастыруда қолдану қажет дейді.

Оқушылар есептi шығару үрдерiсiнде шешiмдердi жалпылау арқылы жаңа бiлiмдердi меңгередi. Психологтар А. А. Смирнов, П. Н. Зинченко егер материалды терең түсiнуге бағытталған оқу әрекетінің белсендi әдiсiн қолданса, есте сақтау өте жоғары болатындығын айтты. Өз күшiнiң арқасында алынған білім есте оңай және көпке дейiн сақталатындығын дәлелдеген.

ТМД және шетел психологтары мен педагогтарының зерттеулері (Л. С. Выготский, А. А. Смирнов, П. Я. Гальперин, В. В Давыдов, Д. Б. Эльконин, А. В. Усова, Ж. Икрамов және т. б) ғылыми ұғымдарды қалыптастырудың жолдары мен әдістерін анықтауға арналған. А. В. Усова ұғымдардың қалыптасуы - ұғым мазмұнына, оқушылардың жалпы даму деңгейіне, олардың бұрынғы іс-тәжірибелеріне, таным қабілеттеріне және т. б байланысты деп есептейді.

Математикалық ұғымды қалыптастыруда логика сияқты интуитивтік түсінік өте қажет. Орта мектепте математикалық анализдің негізгі ұғымдарын есептер арқылы қалыптастырудың басты факторларының бірі интуитивті қабылдау. Ғалым-математик А. Д. Мышкистің пікірінше интуиция дамымайынша білім формальді болады, ол тек ақпараттық-анықтамалық мағынада ғана болады. Сондықтан, оқушының интуитивтік түсінігін пайдаланып ұғым мағынасын жүйелі түрде ашу керек.

Психолог-педагогтардың зерттеулерінде ұғымдарды қалыптастыруда есептерді қолдану үшін оқу мазмұнын есеп түріне келтіру керек делінген.

Есеп арқылы оқыту туралы С. И. Шoхор-Троцкий, Д. Пойа, П. М. Эрдниев, А. М. Фридман, Ж. Икрамов, А. С. Крыговская, Ю. М. Колягиннің еңбектерін оқып-үйрену және талдау нәтижесінде есеп арқылы оқыту әдiсi дегенді - оқушылардың жаңа теориялық материалды белгiлi есептер жүйесiн шығару және оның шешiмдерін жалпылау негiзiнде оқу материалын меңгеруді түсінетін боламыз.

Есептер арқылы оқыту теориялық материалдың мағынасын ашатын есептер жүйесiн дайындау, есептердi мұқият таңдау, оларды белгiлi бiр жүйемен орналастырудан тұрады. Мұғалiм есептерді қолданып оқыту үшін, есептердің мәтіні оқушыға ұғынықты болуы керек, ол проблемалық және ақпараттық сұрақтар, танымдық есептер немесе оқу тапсырмалары түрінде тұжырымдалуы қажет. Оқыту есептерінің жүйесi математикалық обьектiнiң қасиеттерiн анықтайтын тұжырым, жаңа теориялық жағдайдың дәлелдемесi, белгiлi бiр типтегi есептердi шешу алгоритмi болуы мүмкiн.

М. И. Денисовтың зерттеу жұмысында оқыту есептерінің жүйесiн құру үшiн ескерілетін талаптар көрсетілген:

- меңгерiлген бiлiм, бiлiктілік және дағдының жиынтығын алдын ала айқындау;

- өзiндiк таным әрекетiн жетiк ұйымдастыру үшiн iзденiс ситуациясын туғызу;

- жаңа теориялық материалды меңгеру үшiн оқушының оқу түрткiсiн дамыту.

Жоғарыда айтылған талаптарды ескерiп, математикалық анализдің негізгі ұғымдарына байланысты теориялық материалды оқыту есептер жүйесiне келтіріп, қайта өңдеу үшін мыналарды ескеру қажет:

- жаңа оқу материалы жөнiнде терең талдау жасау;

- теориялық материалды есептерді пайдаланып оқыту мүмкiндігін анықтау;

- оқытылатын материалдың курстағы маңыздылығын, пәнішілік байланысын және материалды оқытуға бөлiнген уақытын ескеру;

- оқытылатын материалдың оқу түрткiсi (мотиві) болатын практикалық есептердi құру үшiн оқу материалы мен басқа пәндер арасындағы пән аралық байланысты ескеру;

- жаңа ұғымды сипаттайтын белгілер мен оның қасиеттерiн анықтау;

- оқу материалын оқып-үйрену жоспарын құру, оқу материалы бөлiмдерге бөлініп, әрбiр бөлiмді оқып-үйренгеннен кейiн теориялық тұжырым жасау;

- теориялық материалдың сәйкес бөлiмін оқыту ретіне байланысты есептердi орналастыру.

Есептерді орналастыру кезінде есеп келесi есептердi шығаруға ықпал ететіндей етіп құрылады. Оқушылар оқыту есептері жүйесiндегі есептердiң шешiмдерi кездейсоқ алынбағанына көздерi жетiп, оларды шығарудың қажеттiлiгiн түсiнеді.

Жаңа теориялық білім алуға мүмкіндік беретін практикалық есептерді шығару пайдалы. Практикалық есептер оқушылардың теориялық мағлұматтарға қызығушылығын, зейiнiн ерекше аударады. Ұсынылған есептердiң шешуiн iздестiруге көңiлi ауады, есептердiң шешiмдерiн қорытындылайды, жаңа теориялық білiм алады, теориялық тұжырым жасайды. Мiне, осылайша формальды, жаттанды бiлiм алу жойылады.

Теориялық материалды есеппен немесе есептер жүйесiмен ауыстыру кезінде оқушы теориялық мағлұматтарды игеріп қана қоймай, математикалық бiлiктілік пен дағдыны қалыптастырады. Жаңа материалды бекiтуге арналған есептер санын қысқартуға мүмкiндiк болады. Сонымен қатар математикалық бiлiктілік пен дағдыны қалыптастыруға арналған уақытты үнемдейдi. Оқу үдерісінде оқушылармен жеке жұмыс iстеуге қосымша мүмкiндiктер туады.

Есептер арқылы оқытуда жаңа білімдерді меңгеру әдістерінің бірі есептер шешімдерін жалпылау болып табылады. Есептер математикалық обьектінің мәнін ашатын немесе математикалық обьектінің қасиетттерін көрсететін есеп болуы тиіс.

Математикалық анализдің негізгі ұғымдарын қалыптастырудың тиімділігін артыру үшін негізгі мектептің алгебра және геометрия пәндерін оқыту барысында алдын ала дайындауды жүйелі түрде жүргізу керек. Математикалық анализдің негізгі ұғымдары алдан ала дайындықты қажет ететін математикалық объектілерге жатады. Өйткені әр қадам сайын дербес фактілер мен есептерден жалпыға көше отырып, оқушыларды нақты түсініктерден абстрактылы түсініктерге жетелеуіміз керек. Бұл үдеріс ұзақ мерзімге (6-9 сыныптарда) жүргізіледі, себебі бұл ұғымдар мен бағдарламалық материалдардың арасындағы байланысты анықталып, олардың қолданбалы мәнін көрсетіледі.

Алдан ала дайындық немесе кіріспе шараларының қажеттілігі жөнінде көптеген зерттеулерде жазылған болатын. Д. А. Антоновтың диссертациясында шек ұғымының « » тіліндегі анықтамасына келтіретіндей жаттығулар жүйесін құрастырған. Шек ұғымын мектепте саналы түрде қалыптастыру үшін алдын ала дайындау қажет. Оқушыларды негізгі мектепте шек ұғымының әлі қалыптаспаған тұжырымдамасымен мазмұндық түрде таныстыруға мүкіндік болады. Бұл тек қана мүмкіндік емес, қажеттілік. Өйткені осы кезеңде оқушылардың жас ерекшелігіне қарай интуициялы түрде меңгеруге икемделеді.

Оқушыларды шек және шекке көшу ұғымдарымен 8-сыныпта алғаш рет таныстыруға болады. Мұндай жағдайда қарастыратын мысалдар қарапайым көрнекі-геометриялық сипатта болуы тиіс.

Шек ұғымының мәнін ашуда көрнекі-интуитивтік түрде берілген алдын ала дайындық есебін қарастырайық.

1-мысал. АВС үшбұрышының С төбесі MN түзуінің бойымен бірқалыпты қозғалсын. MN түзуі АВ табанына параллель (1-сурет) . Осындай қозғалыс кезінде АВС үшбұрышының бұрыштарының шамасы, қабырғаларының ұзындығы, периметрі мен ауданының шамасы қандай өзгерістерге түседі?

1сурет - 1-мысалдың геометриялық кескіні

MN түзуінің О нүктесіне қарағанда С нүктесінің абсциссасын 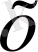әріпімен белгілеп, оның қозғалысын шартты түрде былайша 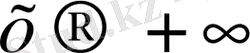жазуға болады.