Бастауышта математикалық білім беру

Пән: Педагогика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 43 бет
Таңдаулыға:

Бастауыш математикалық білім беру ісінің ежелгі замандардағы жайы

Курстың объектісі - тарихи-әдістемелік білім 03. 15 - БОПӘ мамандығы бойынша Қазақстан Республикасы мемлекеттік стандарты талаптарына сәйкес бастауыш сыныптар мұғалімінің жоғары кәсіби педагогикалық білімінің құрамдасы ретінде.

Курстың пәні - бастауыш сыныптар мұғалімінің математиканы оқыту әдістемесінің тарихынан 03. 15 - БОПӘ мамандығы бойынша Қазақстан Республикасы мемлекеттік стандартының талаптарына сәйкес білім, білік және дағдыларын қалыптастыру барысы.

Курстың мақсаты - болашақ бастауыш мектеп мұғалімдеріне әдістемелік-математикалық білімдердің дамуы туралы түсінік беру, бұл тәжірибелерді меңгеру олардың кіші жастағы оқушыларға математиканы оқытып үйретуді және ғылыми ойлаудың логикалық, қатаң түрдегі дағдыларын қалыптастыру болып табылатын кәсіби міндетін орындауға көмектесетіндігін ашып көрсету.

Курстың негізгі міндеті бастауыш мектепте математиканы оқытудың әдістемесінің қалыптасуы мен даму динамикасы туралы білімдерді тереңдете және кеңейте түсу, сондай-ақ өткен кезеңдердегі және кәзіргі күнгі әдістемелік-математикалық ой-пікірдің көрнекті өкілдерінің ғылыми әдістемелік идеяларымен таныстыру болып табылады.

Курс бойынша лекциялар мен практикалық сабақтар, студенттердің өз бетімен орындайтын жұмыстары жүргізіледі.

Лекциялардың басты ерекшелігі, әр сабақта студенттің назары сәйкес кезеңдегі әдістемелік ой-пікірдің даму барысына сипаттама беруге және соның барысында байқалатын жалпы заңдылықтарды ашып көрсетуге аударылады. Практикалық сабақтарда әралуан сипаттағы әдістемелік тапсырмалар (оқу бағдарламаларын, оқулықтарды, әдістемелік құралдарды және т. б. талдау, кіші жастағы оқушыларға математиканы оқытудың әр түрлі жүйелерін, озат ұстаздардың іс-тәжірибелерін талдау, т. с. с. ) орындалады, тарихи-әдістемелік әдебиетпен оны шығармашылық тұрғыда пайдалану бағытындағы жұмыстар жүргізіледі.

Математиканы оқыту пәні ретіндегі пайда болуының негізгі шарты алғашқы қауым адамдарының еңбек әрекетімен қалыптасқан қоғамдық қатынас болып табылады. Бұл балаларды жай қарапайым есептеулер жүргізуге үйретудің практикалық қажеттілігінен туындаған. Осындай білімдерге үйретуге арнайы мекемелер, мектептер құрылды.

Балаларды ұйымдасқан түрде тәрбиелеу мен оқытудың қалыптасуы тарих зерттеулері бойынша, ерте өркениетке ие болған Шығыс елдерінде іске асты. Ерте Шығыста мектептік білім беру тамыры ежелгі дүниеде жатыр. Орта патшалық тұсының (б. э. д. 2050-1700 ж ) өзінде-ақ Мысырда мемлекеттік аппараттың дамуы мен білімді адамдардың қажеттілігінің әлдеқайда өсуінен мектептер пайда болды. Онда балалар жас ерекшеліктері мен білімдеріне байланысты топтарға бөлінді. Мектеп жайлы мәселе Жаңа патшалық (б. э. д 1580-1070 ж. ) дәуіріндегі ескерткіштерде кездеседі. Ежелгі Мысыр мектептерінде арифметика мен геометрияға көп көңіл бөлінген. Мұнда негізінен практикалық есептер басты роль атқарды. Көпшілік жағдайда теориялық түсіндірмелер берілмей, тек мысалдарды жаттап алу және оны практикада қолдану біліктері талап етілді.

Бастауыш білім беру барысында Мысырда математиканы оқуға балалардың көпшілігі тартылғандығын Платон құптады, оның үстіне Платон кезінде (б. э. д. ІVғ. ) білім беру ойын көмегімен іске асырылды. Оқушыларды жаттықтыру үшін оларды қызықтыру, ойнату барысында есептер құрастырылды, олар тікелей практикалық сипатта болған жоқ, тек сондай түрде болды.

Арнайы мекеме түрінде мектептер Вавилонда да Мысырмен шамамен бір уақытта (Орта хандық - б. э. д. ІІІ мыңжылдықтың соңы мен ІІ мыңж. басы ) пайда болды. Ежелгі Вавилонда мектеп «Кесте үйі»деп аталды. Мектептің мақсаты жазғыш мамандығын дайындау болып табылды. Оқушылар сауат ашу, тарих, география, құқық т. б. оқыды. Бұларға қоса математиканы оқу да іске асырылды - ұрпақтан-ұрпаққа оқушылар мысалдардың стандартты жинақтарын көшіріп отырды, ал ол мысалдарда жұмысшыларға ақы төлеу мөлшерін табу, азық-түлікті дұрыс бөлу, егістікті өлшеумен байланысты есептер шешу талап етілді. Негізгі оқытудың әдісі ретінде оқу материалын көшіріп жазу және бірнеше қайталап дауыстап оқудың арқасында жаттау әдісі қолданылды.

Ежелгі уақыттарда Қытайда мектептер пайда болып, беки түсті. Шань-Инь мемлекетінде (б. э. д. ІІ мыңж. ) жоғары дәрежеде дамыған жазу дәстүрі мен соған сәйкес мектептік білім беру негізі өмір сүрді.

Ежелгі Индияда да мектептер дамыды. Ежелгі Индия мәдени дәстүрінің бастауын «Веды»-дан алады. Индия математикасының жоғарғы жетістігі - ондық санау жүйесіндегі қолданылып жүрген қазіргі заманғы цифрларды құру, осылардан арабтар мен еуропалықтардың ондық позициялық жүйелері пайда болған.

Б. э. д. ІV ғ. Мектептер жұмыс істеді, олардың ішінде Платон Академиясы (б. э. д. 428 және 427-348 және 347) және Аристотель Лицейі (б. э. д. 384-322 ж) . Бұларда атақты ғалымдардың айналасына жиналған жас адамдардың аздаған топтары болды және оқыту негізінен ауызша жүргізілді.

Сөйтіп, Ежелгі Грецияда математикалық ғылымның қалыптасуы мен математиканың пайда болуы жеке - дара оқу пәні ретінде іске асты. Осы Грецияда математикадан ірі өзіндік және ерекше еңбектерді туғызған атақты математиктер шықты. Атап айтсақ, Пифагор, Евклид, Евдокс, Архимед, Герон, Диофант т. б. осыларға қарсы, Ежелгі Грецияда математикалық ойдың көрнекті өкілдерінің болғандығын көреміз.

VІІІ - Х ғ. ғ. индия және грек ғалымдарының еңбектері араб тіліне аударылды. ІХ ғ. Ислам елдерінде арифметика және геометрия күшті дамыды.

Л. Н. Гумилевтің айтуына қарағанда, ХVІІІ - ХІХ ғасырлардағы көшпелі тайпалар мәдениетінен көп жоғары болған. Шаруашылықтың әр түрлі салаларын етене ұштастырып отырудың, егіншіліктің, қол өнері мен сәулет өнерінің, әсіресе сауда-саттық ісінің өркендеуі әжептәуір математикалық білім-түсініктерді қажет етті Қазақстан территориясын мекендеген ежелгі халықтарда математиканың бастапқы мағлұматтары қандай деңгейде болғандығы жөніндегі бірсыдырғы тура деректерді көне түріктердің жазба ескерткіштерін талдау арқылы білуге болады.

Түрік тілдес халықтар ерте замандардан бастап-ақ жазба нумерацияны игерген. Мысалы, 1939жылы ертедегі Сарыга қаласының орнын қазу барысында Түркеш қағандығы (699-776ж. ж. ) кезіндегі теңгелер табылған. Соның біріндегі жазуларды аса көрнекті шығыс зерттеушісі А. Н. Бернштам «Затым ” 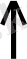“ (он оқ) таңба» деп оқыған. Мұндағы ” 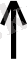“ таңбасы Орхон - Енисей жазбаларында ”оқ“ деп оқылатыны белгілі. Демек, ”=“ - он санының таңбалануы деп топшылауға болады. Майялар қолданған жазбаша нумерация 2000 жыл шамасындай бұрын пайда болған.

Қазіргі қолданылып жүрген цифрлардың шыққан тегі мен отаны туралы әр түрлі пікірлер бар. Ғалымдардың көбісі олардың түп-нұсқасы Үндістаннан шыққан деген пікірді қуаттайды.

Біріншіден, қазіргі цифрлардың түпнұсқасы орал-алтай тілдері тобына жататын халықтардан шыққан. Бұл цифрлар Батыс Европаға түрік ғалымдарының еңбектері арқылы белгілі болған. Екіншіден, ең көне есептеу аспаптарының бірі - абак та осы халықтарда пайда болып, кейіннен Батыс Европаға ауысқан сияқты. Орыс есепшотының түпнұсқасы ХVІ ғасырда Сібірден әкелінген. Ежелгі Қытайда абакқа ұқсас ”суан-пань“ деп аталған есептеу құралы болған. Соған қарағанда абак Сібір мен Қазақстанды мекендеген түрік тілдес халықтарға Қытайдан ауысқан сияқты. Бұл Қазақстан жерін мекендеген ежелгі халықтардың өз шаруашылығы мен тұрмыс-тіршілігіне сай әжептәуір математикалық білім түсініктері болғандығы аңғарылады.

Қытайда Тан династиясы (618-907ж. ж. ) кезінде императорлық академияның оқу жоспарына математика міндетті пән ретінде енгізіліп, шәкірттер оны үзбей 7 жыл бойына оқуға тиіс болған. Шен алу үшін тапсырылатын мемлекеттік емтиханға дайындалу үшін пайдаланылатын оқулықтардың бірі - « Тоғыз кітаптағы математика» атты трактат болған.

«Ұлы жібек жолының» Қазақстан өңірін басып өтуі бір жағынан сауда-саттық ісінің, екінші жағынан Үнді, Қытай, Византия елдерімен мәдени байланыстың күшеюіне ықпал етті. Мысалы, Орта Азияның ұлы ғалымы Ибн-Сина (980-1037) өз жазбаларында жас кезінде әкесінің үнді арифметикасын оқып-үйрену мақсатымен саудагерлерге ілестіріп жіберіп отырғанын баяндайды. Халифаттың орталығы Бағдат қаласында «Бейіт әл-Хикма» («Даналық үйі») құрылып, оған бүкіл шығыс елдерінен атақты ғалымдар шақырылды. «Даналық үйінде» жақсы жабдықталған кітапхана мен астрономиялық обсерватория болды. «Даналық үйінде» Орталық Азия мен Қазақстан өңірінен шыққан ғалымдар әл-Хорезми, Ғаббас, әл-Жауһари, Ферғани, Меруази т. б. жемісті еңбек етті.

2-дәріс. Әдістемелік-математикалық білімдер құрылымындағы

халық педагогикасының орны

Бастауыш қазақ мектебінде математиканы оқыту жөніндегі ғылыми ой-пікірдің қалыптасуының бұлақ-бастауларының бірі - халық педагогикасы болып табылады.

Бабаларымыз өзінің барлық асыл сөз, даналық ойларын мақал-мәтелдер мен нақыл сөздер етіп кейінге қалдырып отырған. Жас жеткіншектерді тәрбиелеу мәселелерімен қатар, білім мен ғылымды игерудің, сондай-ақ математикалық білімнің қажеттігін насихаттау да кең орын алған. «Саны бардың мәні бар», «Есеп, есеп білмеген есек», «Есепсіз дүние жоқ» деп халқымыз текке айтпаған.

Жас балалардың қарапайым математикалық білім-түсініктерін қалыптастыруда санамақтар ерекше рөл атқарған. Қазақтың халық санамақтары, ең алдымен, жас балаға сан үйретудің дидактикалық құралы, әсіресе он көлеміндегі сандардың нумерациясын игертудің әдіс-тәсілдері ретінде қолданылған.

Бір дегенің - білеу. Бір санының таңбасы, яғни бір цифры білеуге ұқсайды.

Екі дегенің - егеу. Қазақта ағаштан ыдыс-аяқ жасағанда оның ішін үңгіп оятын, ұшы қайқы құрал түрі болған. Демек, екі саны егеуге ұқсайтын пішінде таңбаланады.

Үш дегенің - үскі. Үскі - жергілікті тілде бұрғы, тескішсөздерінің синонимі ретінде жұмсалады. Үш санының таңбасы бұрғы тәріздес болатынын бірден байқауға болады.

Төрт дегенің - төсек. Төрт санының таңбасы қазақтың төсек ағашының пішініне ұқсайтыны көрініп тұр.

Бес дегенің -бесік. Бұл жерде бестің таңбалануы ”бесік жамбыға“ұқсас екендігі меңзеліп тұрған сияқты. Бесік жамбы-бесік формасында құйылған күміс не алтын.

Алты дегенің - асық. Алты санының таңбалануы ”асық жамбы“ пішіндес. Асық жамбы - үлкендігі қой асығы көлеміндей алтын яки күміс.

Жеті дегенің - желке . Бұл жерде жеті санының таңбалануы қазақ қолөнеріне қатысы бар желкелік сөзімен байланысты деп ойлаймыз. Желкелік: 1) жүгеннің екі жақтауының желкеде түйісетін ұшы; 2) киім жағасының астына қадалған ілгек (бау) .

Сегіз дегенің - серке. Сегіздің таңбалануын серкенің мүйізіне ұқсату болуы мүмкін.

Тоғыз дегенің - торқа. Тоғыздың таңбалануы оралған матаның кескініне ұқсайды. Торқа - ең қымбат жібек мата.

Он дегенің - оймақ. Оймақ - іс тіккенде саусаққа ине, жуалдызбатпау үшін пайдаланылатын, темірден, жезден, күмістен жасалған құрал. Оймақ кейде былғарыдан, көннен де жасалады, оймақ саусақтың басына кигізіледі. Демек, он саны саусақ пен оның қасындағыоймақ пішіндес ноқат арқылы таңбаланады.

Қазақтың халық педагогикасында жаңылтпаштар мен жұмбақтардың да алатын өзіндік орны ерекше.

Сан мен санау мәселелеріне байланысты болып келетін жаңылтпаштар баланың тілін ширатып, оны дұрыс және айқын сөйлеуге үйретумен бірге, сандардың атауларын дұрыс айта білуін қалыптастыруға да игі әсерін тигізеді. Қазақ арасында есеп сипатында тұжырымдалатын жаңылтпаштар да көптеп кездеседі.

Мәселен,

Сырық-қырық, немесе Үш кіші ішік піштім,

Құрық-қырық, Бес кіші ішік піштім,

Қанша болды, Неше кіші ішік піштім?

Құрық, сырық?

деген сияқты жаңылтпаштар, бір жағынан, балаға сандардың аталуын дұрыс айта білу мақсатымен берілсе, екінші жағынан, есеп шартындағы байланысты аңғара отырып, осының негізінде сәйкес арифметикалық амалды дұрыс таңдап ала алуды талап етеді.

Жұмбақтарды қазақ халқы басқа да тапқырлық сөздер қатарында жас жеткіншектің ойын тапқырлыққа баулу үшін, сонымен бірге оның сан жөніндегі түсініктерін байытып, онан әрі дамытудың әдістемелік құралы ретінде де қолданып отырған.

Ұрпақтан-ұрпаққа жалғасып, осы күнге дейін жетіп отырған халқымыздың ауызша есептерінің жас балаларға математикалық білім берудің өзгеше бір әдістемелік құралы ретіндегі маңызы орасан зор. Мәселен, қазіргі бастауыш мектепте оқушылардан есептерді, көбіне, жазбаша шығару талап етіледі. Ал, қазақ халқының есептерінің мазмұны әрқилы болып келетіндіктен, баланың мұнда дағдылы, үйреншікті әдіс-тәсілдерді қолдануға мүмкіндігі бола бермейді. Бала әрбір жағдайда есепті шығарудың дұрыс, лайықты және ең қолайлы жолын өздігінен табуға тырысады. Бұл тұрғыдан алғанда, қазақ халқының ауызша есептерінің қазіргі мектеп үшін таза әдістемелік жағынан да зор маңызы бар екендігі аңғарылады.

Сонымен, қорыта айтқанда, ата-бабаларымыз ежелгі замандардан бастап-ақ жас балаларға тиянақты тәрбие берумен қатар, олардың математикалық білім-өрісін кеңейтуге де көңіл бөліп отырған. Бұл қазақ отбасында санамақтар, жұмбақтар, жаңылтпаштар, мақал-мәтелдер және ауызша есептер арқылы жүзеге асырылған. Ендеше, қазақ бастауыш мектебінде математиканы оқыту жөніндегі ғылыми ой-пікірдің бастау-бұлақтарының бірі болып табылатын халық педагогикасындағы әдістемелік-математикалық тенденцияларды зерттеп, оған дұрыс ғылыми талдау жасаудың маңызы ерекше.

3-дәріс. Орта Азиялық және қазақстандық ғалымдардың әдістемелік-математикалық көзқарастары

VІІІ ғасырда Орта Азия мен Қазақстанға араб басқыншылары баса көктеп кірді. Арабтар ең алдымен, жергілікті халықтар тұтынған діни нанымдарды түбірімен құртып, оның орнына жаңа мұсылман дінін енгізуге күш салды. Жергілікті тілдерде кітаптар жазуға, мектептер ашуға тыйым салды. Араб тілі халықаралық тілге айналды. Оны білу әрбір мұсылманға міндетті болды. Осының салдарынан жергілікті халықтардың тарихи ескерткіштері, байырғы мәдени және ғылыми мұралары жойылып кетті. Осыған байланысты халифаттың орталығы Бағдат қаласында ”Бейіт әл-Хикма“ ( «Даналық үйінде») құрылып, оған бүкіл шығыс елдерінен атақты ғалымдар шақырылды. «Даналық үйінде» жақсы жабдықталған кітапхана мен астрономиялық обсерватория болды. Онда грек және үнді тілдеріндегі қолжазбаларды араб тіліне аударумен қатар, жаңа бағыттағы ғылыми-зерттеу жұмыстары дұрыс жолға қойылып, араб тілінде ғылыми еңбектер жазу қызуқолға алынды. «Даналық үйінде» Орта Азия мен Қазақстан өңірінен шыққан ғалымдар әл-Хорезми, Ғаббас әл-Жауһари, Ферғани, Меруази т. б. жемісті еңбек етті.

Әл-Хорезмидің ұлы ғалым ретінде даңқын шығарған математикалық мұраларының ішірдегі ең бастылары мына екі кітап: «Китап әл-джәм-уәт тафрик би-хисаб әл-үнді» («Үнді есебі бойынша қосу мен азайту кітабы») және «әл-Китаб әл-мұхтасарфи хисаб әл-джәбр уәл-мүкәбәлә» («әл-джәбр мен уәл-мүкәбәла есебі жөніндегі қысқаша кітап») . Бұлардың біріншісінде арифметика, ал екіншісінде алгебра баяндалған. әл-Хорезмидің бұл екі еңбегі әлемдік математика ғылымының асыл маржандары болып табылады.

«Даналық үйінде» қызмет атқарған басқа ғалымдар ішінен Қазақстан топырағынан шыққан Ғаббас ибн Саид әл-Жауһариды атап өту қажет. Ол ежелгі грек геометрі Евклидтен кейінгі «Екінші Евклид» деген құрметті атаққа ие болған. әл-Жауһари Евклидтің ”Негіздеріне“ түсініктемелер ретінде жазылған трактаттардың авторы және ол шығысматематиктері ішінен бірінші болып Евклидтің атақты бесінші постулатын дәлелдеуге әрекеттенген. М. Ө. Ысқақовтың айтуына қарағанда, ол математика мен астрономиядан көптеген еңбектер жазған. Дүние жүзінің көптеген геометрлері әл-Жауһаридың еңбектерімен жақсы таныс болған және оны өздеріне ұстаз тұтқан.

Қазақстан топырағынан шыққан, дүниежүзілік ғылым мен мәдениеттің дамуына зор ықпал еткен ірі тұлғалардың бірі - Әбунәсір әл-Фараби (870-950ж. ж. ) . Оның сан-салалы трактаттары ғылымның барлық салаларын қамтиды. Ұлы ойшыл шығармаларында педагогика мен психология, сондай-ақ математика мен оны оқытудың әдістемесі мәселелері де ерекше орын алады. «Ғылымдардың классификациясы» деген еңбегінде математика ғылымын жеті тарауға бөлген: 1) Арифметика; 2) Геометрия; 3) Оптика; 4) Астрономия. 5) Музыка. 6) Салмақ туралы ғылым. 7) Айла-әрекет туралы ғылым.

Фарабише, оқу мен оқыту, ойды білдіру, мәселенің мазмұнын баяндау, сұрақ беру мен жауап қайыру жағынан алғанда математика тіл ғылымы, граматика, логика және поэтидан кейін келеді. Ерекше көңіл аударарлық жайт, ол арифметика, геометрия, астрономия және музыканы педагогикалық ғылымдар деп атайды да, олардың тәрбиелік маңызын ашып көрсетеді.

Орта мектепте «Геометрия» пәнін оқыту Фараби айтқандай, «ақылға сәйкес мынадай схема бойынша жүргізіледі: {нүкте} {түзу} {геометриялық фигуралар} {дене}.

Қазақстан өңірінен Фарабиден кейін де ғылымның сан алуан салалары бойынша өзіндік ой-толғаныстарымен мәшһүр болған көптеген ғұламалар шықты. Олардың ішінен әлам ад-Дин әл-Жауһари (Х-ХІғ. ғ. ), Ахмет Фараби (ХІ-ХІІ ғ. ғ. ), Жамал ад-Дин Түркістани (ХІІІ-ХІV ғ. ғ. ) сияқты ғалымдарды ерекше атап өтуге болады.

әлам-ад-Дин әл - Жауһари - қазіргі Оңтүстік Қазақстан жеріндегі Фараб маңындағы Жауһардан шыққан математик, астрономиялық аспаптардың шебері болған. Ол математика саласындағы аса күрделі еңбектерімен, астрономиялық аспаптар жасауда және пайдалануда асқан шеберлігімен танымал ғалым, оның тамаша шығармалары кең таралған.

Ахмет Фараби - Отырар аймағынан шыққан математик, «Китаб тадбир ал-хавз фи тадвир ал-ахваз» ( ”Су алаптарын дөңгелек су алабы етіп салу туралы кітап“) атты еңбегімен белгілі. Оның бұл шығармасы дөңгелекті квадратуралау мәселесіне арналған.

Жамал ад-Дин Түркістани - Түркістаннан шыққан, математика мәселелерімен айналысқан ғалым. Ол 1312 жылы өз заманасы үшін озық деп саналған және медреселерде кеңінен пайдаланылған «Китаб әл-әлайна» («Жоғары математика кітабы») атты трактат жазған.

Орта ғасырларда бастауыш математиканы оқыту жөніндегі ой-пікірдіңжоғары деңгейге көтерілуі әл-Фараби сияқты ”кәсіпқой“ математиктердің әрекеттерімен ғана шектелмейді. Ол сонымен қатар ойшыл ақындардың, сөз зергерлері мен дуалы ауыз даналардың сан-салалы көзқарастарынан да көрініс береді.

Қараханидтер тұсында (ХІ-ХІІ ғасырлар) ислам дінінің таралуынакең жол ашылғанымен, барлық мәселеде үстем болып келген араб тілінің қолданылу аясы тарыла бастады. Сөйтіп қыпшақ, оғыз, қарлұқ және ұйғыр тайпалары мен халықтарының тілдері негізінде Х-ХІІ ғасырларда түрік жазуы қалыптасты. Осының нәтижесінде Ж. Баласағұн, А. Жүйнеки сияқты ойшылдардың тәлім-тәрбиелік мәні зор шығармалары жазылып, кеңінен тарады. Бұлардың ішінде Жүсіп Баласағұнның (ХІғ. ) ”Құтадғу білік“ атты кітабын ерекше атап айтуға болады. Түрік халықтарының мәдени өмірінен, тәлім-тәрбиелік ой-пікір, тәжірибелерінен мол мағлұмат беретін бұл шығармада математикалық білімнің қажеттігін насихаттайтын құнды пікірлер де көптеп кездеседі.

”Құтадғу білік“ математикалық білімнің және оны игерудің қажеттігі тұрғысынан құнды кеңестер келтіріледі. Ең бастысы, математикалық білімнің қоғамдық мән-маңызы жан-жақты ашып көрсетіледі. Әрине, кіпаптағы нақыл-өсиеттерді әдістемелік-математикалық ой-пікір дәрежесінде бағалауға бола қоймас. Солай дегенмен Ж. Баласағұнның математикалық білім алуға шақырған өсиеттерінің зор тәлім-тәрбиелік мәні бар деп білеміз.

4-дәріс. Бастауыш мектепте математиканы оқыту әдістемесінің пайда болуындағы алғашқы қадамдар

ХІХ ғ. басында Батыс Еуропада бастауыш білім беру жүйесінде ірі өзгертулер болды. Джон Локк, Жан-Жак Руссо, Клод Адриан Гельвеций, Дени Дидро және т. б. теоретик - педагогтардың педагогикалық ой-пікірлері оқыту мен тәрбиелеу процесін құрудың жаңа негізін салды. Мектептік білім берудің ірі реформаторының бірі, жоғарыдағылардың ой-пікірлерін тәжірибеге енгізуші Щвейцар педагогы Генрих Песталоцци (1746-1828ж. ж. ) болды. Оқыту процесін түбегейлі жаңартқан Песталоцци арифметиканы оқыту әдістеріне де елеулі өзгерістер енгізді. Оның "Очевидного учения о содержании чисел книга"(үш томдық) 1806ж. және "Азбука очевидности или очевидное учение о содержании мер" (екі томдық) 1807ж. еңбектері бар.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.