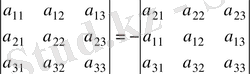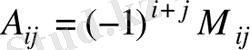Сызықтық алгебра және аналитикалық геометрия негіздері


1. Матрица дегеніміз не? m жатық n тік жолдан құрылған кестені mxn өлшемді матрица деп атайды.
Матрицаны құрайтын сандар матрица элементтері деп аталады. Әдетте матрица латын алфавитінің бас әріптерімен, ал элементтері сәйкес кіші әріптермен белгіленеді:

Қысқаша жазылуы:
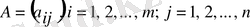
Матрица элементінің бірінші индексі жатық жол нөмірі, ал екінші индексі тік жол (бағана) нөмірін көрсетеді. Мысалы,
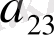 элементі екінші жатық жол мен үшінші тік жол қиылысында орналасқан.
элементі екінші жатық жол мен үшінші тік жол қиылысында орналасқан.
Бір ғана жатық жолдан құралған матрицаны жол-матрица , ал бір ғана тік жолдан құралған матрицаны бағана-матрица деп атайды:
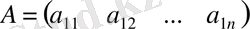 - жол-матрица;
- жол-матрица;
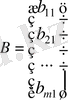 - бағана матрица.
- бағана матрица.
Жол матрица мен бағана матрицаны кейде вектор деп те айта береді.
Жатық жолдар саны мен тік жолдар саны тең болатын матрица квадрат матрица деп аталады,
.
Квадрат матрицаның
 элементтері
диагоналдық элементтер
деп аталады да, матрицаның
негізгі диагоналін
құрайды. Ал
элементтері
диагоналдық элементтер
деп аталады да, матрицаның
негізгі диагоналін
құрайды. Ал
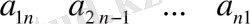 элементтері
қосымша диагоналдық элементтер
деп аталады да, матрицаның
қосымша диагоналін
құрайды.
элементтері
қосымша диагоналдық элементтер
деп аталады да, матрицаның
қосымша диагоналін
құрайды.
Квадрат матрицаның негізгі диагоналінің астындағы немесе үстіндегі элементтері нолге тең болса, матрица үшбұрышты матрица деп аталады,
,
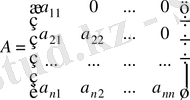
Диагоналды емес элементтерінің бәрі нолге тең болатын квадрат матрица диагоналды матрица деп аталады,
 .
.
Барлық диагоналды элементтері бірге тең болатын диагоналды матрица бірлік матрица деп аталады және оны Е әрпімен белгілейді,
 .
.
Барлық элементтері нолге тең матрица нолдік матрица деп аталады.
МАТРИЦАЛАРҒА ҚОЛДАНЫЛАТЫН АМАЛДАР
1. Матрицаны санға көбейту . Матрицаны санға көбейту үшін оның барлық элементтерін сол санға көбейту керек:

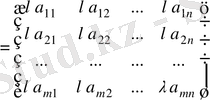
Осыдан матрицаның барлық элементтерінің ортақ көбейткішін матрица алдына шығаруға болатынын аңғару қиын емес.
2. Матрицаларды қосу және алу
.
Өлшемдері бірдей матрицаларды ғана қосуға болады.
 және
және
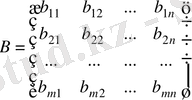 матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:
матрицаларының қосындысы деп элементтері осы матрицалардың сәйкес элементтерінің қосындысы болатын, А + В матрицаны айтамыз:
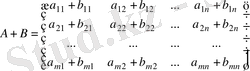 .
.
А матрицасынан В матрицасын алу үшін А матрицасына В матрицасын -1-ге көбейтіп қосу жеткілікті:
A - B = A+(-1) B
немесе А матрицасының әр элементінен В матрицасының сәйкес элементтері алынады. Мысалы А матрицасынан В матрицасын алайық:
3. Матрицаларды көбейту. Бірінші матрицаның тік жолдар саны мен екінші матрицаның жатық жолдар саны тең болған жағдайда ғана екі матрицаны көбейтуге болады. Өлшемі m x k болатын А матрицасы мен өлшемі k x n болатын В матриасы берілсін:
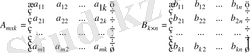
Осы екі матрицаны көбейткенде өлшемі m x n болатын көбейтінді С матрица аламыз:
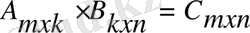
С матрицасының
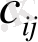 элементі
А
матрицаның
элементі
А
матрицаның
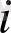 -жатық жол элементтерін
В
матрицаның
-жатық жол элементтерін
В
матрицаның
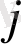 -тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:
-тік жолының сәйкес элементтеріне көбейтіп қосқанға тең болады:
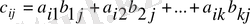 ,
,
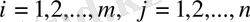 . (1)
. (1)
Қосу және көбейту амалдарының мынадай қасиеттері бар:
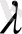 (AB) =(
(AB) =(
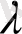 A) B=A(
A) B=A(
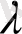 B)
B)
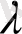 (A+B) =
(A+B) =
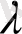 A+
A+
 B
B
Матрицаны транспонерлеу.
Қандай да бір
А
матрицасының жатық жолын сәйкес тік жол етіп жазғаннан пайда болған матрицаны берілген матрицаның
транспонерленген матрицасы
деп атайды да,
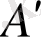 деп белгілейді. Берілген матрицаның өлшемі
m
x
n
болса, оның транспонерленген матрицасының өлшемі
n
x
m
болады
деп белгілейді. Берілген матрицаның өлшемі
m
x
n
болса, оның транспонерленген матрицасының өлшемі
n
x
m
болады
2 Екінші ретті квадрат матрица анықтауышы дегеніміз не?
.
Екінші ретті матрицаның
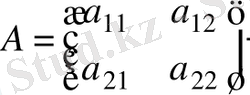 анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады:
анықтауышы немесе екінші ретті анықтауыш деп мынадай санды айтады:
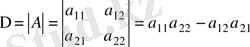
Ал үшінші ретті матрицаға
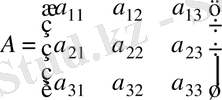 үшінші ретті анықтауыш сәйкес келеді:
үшінші ретті анықтауыш сәйкес келеді:
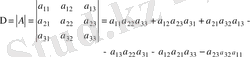 .
.
1-қасиет. Анықтауыштың жатық жолдарын сәкес тік жолдарымен алмастырғаннан, яғни транспонерлегеннен, анықтауыш мәні өзгермейді:
.
Теңдіктің дұрыстығын анықтауыштарды есептеу арқылы тексеруге болады.
2-қасиет. Анықтауыштың қандай да бір жолының ортақ көбейткішін анықтауыш алдына шығаруға болады. Үшінші ретті анықтауыштың екінші жолындағы ортақ көбейткішті анықтауыш алдына шығарамыз:
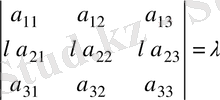
.
Теңдіктің дұрыстығына берілген матрицаны екінші жол бойынша жіктеп тексеруге болады.
3-қасиет. Анықтауыштың екі жолының орнын ауыстырғаннан анықтауыш таңбасы қарама-қарсы таңбаға өзгереді. Үшінші ретті анықтауыштың бірінші және екінші жолдарын алмастырайық:
Теңдіктің дұрыстығын екінші анықтауышты бірінші жол бойынша жіктеп тексеруге болады.
4-қасиет. Егер анықтауыштың екі жолы бірдей болса, онда анықтауыш мәні нолге тең. Үшінші ретті анықтауыштың бірінші және екінші жолдары бірдей болсын:
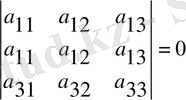 .
.
Теңдіктің дұрыстығын осы екі жолдың орндарын алмастырып 3-қасиетті қолданып тексеруге болады.
5-қасиет.
Анықтауыштың бір жолын қандай да бір санға көбейтіп басқа жолға қосқаннан анықтауыш мәні өзгермейді.
Үшінші ретті анықтауыштың бірінші жолын
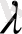 -ға көбейтіп екінші жолға қосайық:
-ға көбейтіп екінші жолға қосайық:
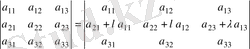 .
.
Теңдіктің дүрыстығын екінші анықтауышты мынадай
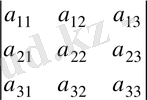 +
+
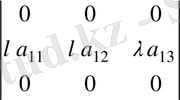
анықтауыштардың қосындысы түрінде жазайық. Сонда бірінші қосылғыш берілген анықтауыш болады да, екінші анықтауыш нолге тең.
6-қасиет. Үшбұрышты матрицаның анықтауышы диагональ бойындағы элементтердің көбейтіндісіне тең:
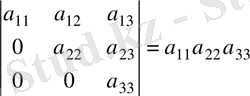 .
.
3. n-ретті квадрат матрица берілген. Осы матрицаның
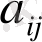 элементінің миноры дегеніміз не?
элементінің миноры дегеніміз не?
n-ретті квадрат матрицаның
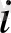 -жатық жолы мен
-жатық жолы мен
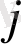 -тік жолын сызып тастағаннан кейін пайда болған (n-1) -ретті анықтауықты
-тік жолын сызып тастағаннан кейін пайда болған (n-1) -ретті анықтауықты
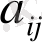 элементінің миноры деп атайды және
элементінің миноры деп атайды және
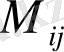 деп белгілейді
.
деп белгілейді
.
Үшінші ретті марицаның
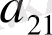 элементінің миноры мынадай екінші ретті анықтауыш болады:
элементінің миноры мынадай екінші ретті анықтауыш болады:
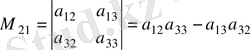 .
.
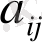 элементінің алгебралық толықтауышы деп мынадай санды айтады:
элементінің алгебралық толықтауышы деп мынадай санды айтады:
Үшінші ретті марицаның
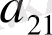 элементінің алгебралық толықтауышы мынадай сан:
элементінің алгебралық толықтауышы мынадай сан:
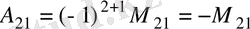
Лаплас теоремасы.
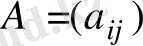
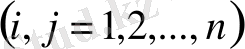 квадрат матрицаның Δ анықтауышы оның кез келген жол элементтерін сәйкес алгебралық толықтауыштарға көбейтіп қосқанға тең:
квадрат матрицаның Δ анықтауышы оның кез келген жол элементтерін сәйкес алгебралық толықтауыштарға көбейтіп қосқанға тең:
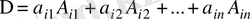
- бұл анықтауыштың i -жатық жолы бойынша жіктелініп есептелуі.
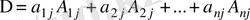
- бұл анықтауыштың j -жатық жолы бойынша жіктелініп есептелуі.
4. n-ретті квадрат матрица берілген. Осы матрицаның кері матрицасы дегеніміз не?
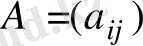
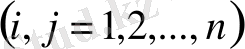 квадрат матрица қарастырайық.
квадрат матрица қарастырайық.
Анықтама. Анықтауышы нолге тең матрица ерекше , ал нолге тең емес матрица ерекше емес матрица деп аталады .
А квадрат матрица үшін мына
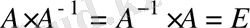
теңдікті қанағаттандыратын
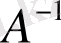 матрица А матрицаның
кері матрицасы
деп аталады
.
матрица А матрицаның
кері матрицасы
деп аталады
.
Кері матрицаны мына формуламен табады:
 ,
,
мұндағы
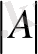 -матрица анықтауышы, ал
-матрица анықтауышы, ал
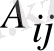 -берілген матрицаның
-берілген матрицаның
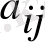 элементтерінің алгебралық толықтауыштары,
i=1, 2, …, n; j=1, 2, …, n.
элементтерінің алгебралық толықтауыштары,
i=1, 2, …, n; j=1, 2, …, n.
Кез келген квадрат матрицаның кері матрицасы бола бермейді.
Теорема
(кері матрица болуының қажетті және жеткілікті шарты) .
Матрицаның кері матрицасы болуы үшін ол ерекше емес (
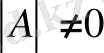 ) матрица болуы қажетті және жеткілікті
) матрица болуы қажетті және жеткілікті
5. n-ретті квадрат матрица берілген. Осы матрицаға жасалатын элементар түрлендірулер дегеніміз не?
Берілген матрицаға кері матрицаны элементар түрлендірулер әдісімен де табуға болады. Бұл әдіс матрицаға элементар түрлендірулер қолдануға сүйенеді . Матрицаның элементар түрлендірулері деп мынадай түрлендірулерді айтамыз:
- Матрицаны транспонерлеу;
- Жолдардың орнын алмастыру;
- Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейту;
- Қандай да бір жолдың барлық элементтерін нолден өзге санға көбейтіп басқа жолдың сәйкес элементтеріне қосу;
- Барлық элементі ноль болатын жолды алып тастау.
Енді кері матрица табу ережесіне көшейік: Берілген
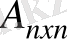 матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда
матрицаның оң жағына бірлік матрица жалғап жазу керек. Сонда
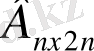 өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында
өлшемді кеңейтілген матрица пайда болады. В матрицаға А матрицасының орнында бірлік матрица пайда болғанға дейін жатық жолдарына элементар түрлендірулер жасалады. Нәтижесінде бірлік матрицаның орнында
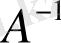 кері матрица пайда болады.
кері матрица пайда болады.
6. Матрица рангсі дегеніміз не?
. Анықтама. Матрицаның нолге тең емес минорларының ең үлкен реті матрица рангісі деп аталады :
r=r(A) = rangA .
Анықтамадан бірден мынадай тұжырымдар жасауға болады:
1.
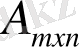 матрицасының рангісі оның өлшемдерінің кішісінен артпайды:
матрицасының рангісі оның өлшемдерінің кішісінен артпайды:
r(A)
 min(m, n) .
min(m, n) .
2. Барлық элементтері ноль болғанда ғана (нолдік матрица) матрица рангісі ноль болады.
3. n-ретті квадрат матрица ерекше емес болғанда матрица рангісі n-ге тең болады.
Матрица өлшемі
n
х
m
, оның рангісі n-тен артпайды,
r(A)
 min
(n, m)
. Егер n-ші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі n-ге тең болады.
min
(n, m)
. Егер n-ші ретті минорлардың ең болмағанда біреуі нолден өзгеше болса, онда матрица рангісі n-ге тең болады.
Теорема. Элементар түрлендірулер матрица рангісін өзгертпейді.
Дәлелдеуі. Матрицаға элементар түрлендірулер жүргізгенде оның анықтауышы не өзгермей сақталады, не нолге тең емес санға көбейтіледі. Яғни, оның реті өзгермейді деген сөз. Олай болса, нолден өзгеше минорлардың немесе матрица рангісінің реті де өзгермейді.
Осы теореманы ескеріп, элементар түрлендірулер жасап, берілген матрицаны барлық диагоналдік элементтері нолден өзгеше болатындай етіп сатылы түрге келтіреміз:
 ,
,
мұндағы
r
 п.
Осы шарттың орындалуын матрицаны транстонерлеу арқылы қамтамасыз етуге болады.
п.
Осы шарттың орындалуын матрицаны транстонерлеу арқылы қамтамасыз етуге болады.
Сонда матрицаның r -ретті нолден өзге миноры

бар болады да, матрица рангісі r- ге тең болады, яғни
r(A) =r.
7. n белгісізді m теңдеуден сызықты теңдеулер жүйесін жаз.
. n белгісізді m теңдеуден тұратын жүйе деп мынадай жүйені айтады: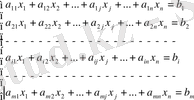 (1)
мұндағы
(1)
мұндағы
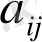 (i=1, 2, …, m, j=1, 2, …, n) -
теңдеу коэффициенттері деп, ал
(i=1, 2, …, m, j=1, 2, …, n) -
теңдеу коэффициенттері деп, ал
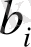 (i=1, 2, …, m) -
бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:
(i=1, 2, …, m) -
бос мүшелері деп аталады. (1) теңдеудің қысқаша жазылуы мынадай:
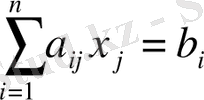 (i=1, 2, …, m)
(1’)
(i=1, 2, …, m)
(1’)
- жүйенің бос мүшелерінің бәрі нолге тең болса,
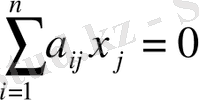 (i=1, 2, …, m)
(2)
(i=1, 2, …, m)
(2)
жүйе біртекті жүйе деп аталады.
Жүйенің әрбір теңдеуін тепе-теңдікке айналдыратын
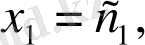
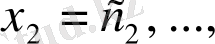
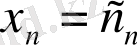
сандар тізбегі
теңдеулер жүйесінің шешімі
деп аталады. Осы шартты қанағаттандыратын барлық
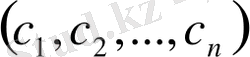 шешімдер
шешімдер жиынын
құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді.
шешімдер
шешімдер жиынын
құрады. Жүйенің шешімдер жиынын табу процесін жүйені шешу дейді.
(1) жүйенің ең болмағанда бір шешімі болса жүйе үйлесімді , ал шешімі болмаса үйлесімсіз деп аталады.
Үйлесімді жүйенің бір ғана шешімі болса, жүйе анықталған , ал шешімі бірден көп болса анықталмаған деп аталады.
Енді (1) жүйеге мынадай белгілеулер енгізейік:
 ,
,
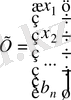 ,
,
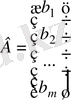
А - жүйе коэффициенттерінен құрылған матрица немесе жүйе матрицасы, Х - жүйенің бос мүшелерінен құрылған бағана матрица, В - жүйенің бос мүшелерінен құрылған бағана матрица. Осы белгілеулерді қолданып (1) жүйені былайша жазуға болады:
АХ=В (3)
(3) теңдеу (1) жүйенің матрицалық жазылуы болып табылады.
Егер жүйе матрицасына бос мүшелер матрицасын жалғап жазсақ,

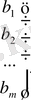 ,
,
жүйенің кеңейтілген матрицасын аламыз.
Кронеккер-Капелли теоремасы. Егер сызықты теңдеулер жүйесінің негізгі матрицасы мен кеңейтілген матрицасының ранглері тең болса, онда жүйе үйлесімді болады.
Теорема бойынша жүйе үйлесімді болуы үшін
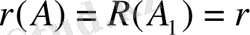 болуы керек. Бұл кезде
r
жүйе рангісі
деп аталады.
болуы керек. Бұл кезде
r
жүйе рангісі
деп аталады.
Үйлесімді жүйенің рангісі жүйедегі белгісіздер санына тең болса (r=n) , онда жүйе анықталған болады, ал егер жүйенің рангісі жүйедегі белгісіздер санынан кем болса (r<n) , онда жүйе анықталмаған болады.
8. n белгісізді n теңдеуден тұратын сызықты теңдеулер жүйесін жаз.
. Бұл әдіс жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n , қолдануға болады. Демек, жүйе түрі мынадай болады:
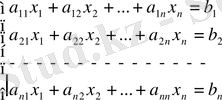 (4)
(4)
Жүйедегі теңдеулер саны мен белгісіздер саны тең, онда жүйе матрицасы квадрат матрица болады. Сол квадрат матрицаның анықтауышын
 деп белгілейік:
деп белгілейік:

Крамер ережесі
.
 -жүйе анықтауышы, ал
-жүйе анықтауышы, ал
 -
-
 анықтауыштың j-тік жолын бос мүшелермен алмастырғаннан пайда болған анықтауыш болсын. Сонда, егер
анықтауыштың j-тік жолын бос мүшелермен алмастырғаннан пайда болған анықтауыш болсын. Сонда, егер
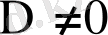 болса жүйенің жалғыз шешімі бар болады және мынадай формуламен табылады:
болса жүйенің жалғыз шешімі бар болады және мынадай формуламен табылады:
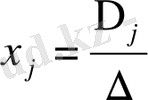 (i=1, 2, …, n)
(i=1, 2, …, n)
9. n белгісізді n теңдеуден тұратын сызықты теңдеулер жүйесін жаз.
Бұл әдіс те жүйедегі теңдеулер саны мен белгісіздер саны тең болғанда, яғни m=n , қолдануға болады. Жүйенің матрицалық жазылуын қарастырайық:
АХ=В,
мұндағы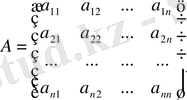 ,
,
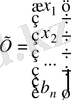 ,
,
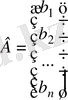 .
.
Айталық
А
ерекше емес матрица болсын, яғни матрица анықтауышы нолге тең емес, олай болса әр уақытта
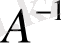 кері матрицасы бар болады. Теңдеуді сол жағынан кері матрицаға көбейтейік,
кері матрицасы бар болады. Теңдеуді сол жағынан кері матрицаға көбейтейік,
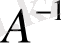 АХ=
АХ=
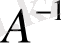 В
В
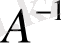 А=E
болатындықтан,
А=E
болатындықтан,
ЕХ=
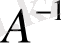 В,
В,
кез келген матрицаның бірлік матрицаға көбейтіндісі сол матрицаның өзіне тең болатындықтан, ЕХ=Х:
Х=
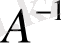 В.
В.
Сонымен, кері матрицалық әдіс бойынша жүйенің шешімін табу үшін бос мүшелерден құралған матрицаны жүйе матрицасының кері матрицасына сол жағынан көбейту керек екен .
10. n белгісізді m теңдеуден тұратын сызықты теңдеулер жүйесін жаз.
n белгісізді m теңдеуден тұратын жүйе қарастырайық,
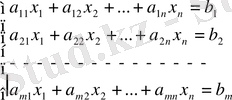 .
.
Гаусс әдісі - жүйедегі айнымалыларды түрлендірулер көмегімен біртіндеп жойып, жүйені сатылы түрге келтіріп, айнымалыларды біртіндеп табатын әдіс. Гаусс түрлендірулері мынадай:
- Кез келген екі теңдеудің орындарын ауыстырып жазу;
- Кез келген теңдеудің екі жағын нолден өзге санға көбейту;
- Қандай да бір теңдеуді нолден өзге санға көбейтіп, басқа теңдеуге сәйкесінше қосу;
- 0=0түріндегі теңдеуді сызып тастау.
Гаусс түрлендірулерін жүйенің өзіне қолданғаннан гөрі оның кеңейтілген матрицасына қолданған ұтымды болады. Олай болса жүйенің кеңейтілген матрицасын қарастырайық,

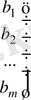 .
.


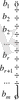
Матрицаның элементтері
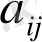 арқылы белгіленіп тұрғанымен, шын мәнінде олар түрлендірулер нәтижесінде өзгерген. Бұл белгілеулер жазуды ықшамдау үшін ғана пайдаланылып отыр.
арқылы белгіленіп тұрғанымен, шын мәнінде олар түрлендірулер нәтижесінде өзгерген. Бұл белгілеулер жазуды ықшамдау үшін ғана пайдаланылып отыр.
Соңғы матрицаға сәйкес келетін теңдеулер жүйесі мынадай:
 (6)
(6)
Соңғы
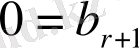 , . . . ,
, . . . ,
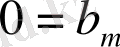 теңдеулеріндегі
теңдеулеріндегі
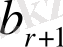 , . . . ,
, . . . ,
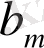 сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады.
сандарының ең болмағанда біреуі нөлден өзгеше болса, онда берілген теңдеулер жүйесі үйлесімсіз, ал бәрі нолге тең болса жүйе үйлесімді болады.
Жүйенің рангісі жүйедегі белгісіздер санынан кем болса, онда жүйе анықталмаған болатыны жоғарыда айтылған. Айталық (6) жүйе үйлесімді және r<n болсын.
Егер
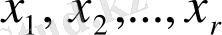 коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда
коэффициенттерінен құрылған анықтауыш нолден өзгеше болса, онда
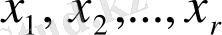 айнымалыларды
базистік (негізгі) айнымалылар
деп, ал басқа
n-r
айнымалыларды
еркін (негізгі емес) айнымалылар
деп атайды.
айнымалыларды
базистік (негізгі) айнымалылар
деп, ал басқа
n-r
айнымалыларды
еркін (негізгі емес) айнымалылар
деп атайды.
Еркін айнымалылары нолге тең болған кездегі шешім
базистік шешім
деп аталады. Базистік шешімдер саны
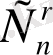 -ден артпайды.
-ден артпайды.
11. Кеңістікте координаталары белгілі
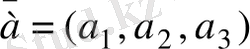 және
және
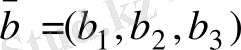 векторлары берілген
.
векторлары берілген
.
. Басы А, соңы В нүктесі болатын бағытталған кесінді вектор деп аталады.
Вектордың ұзындығы оның координаталарының квадраттарының қосындысынан алынған квадрат түбірге тең:
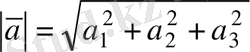
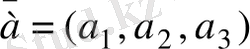 және
және
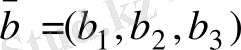 векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады:
векторлары координаталарымен берілген болса олардың қосындысы мынадай түрде анықталады:
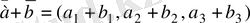
Ал
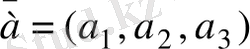 векторын
векторын
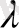 санға көбейту мынадай түрде анықталады:
санға көбейту мынадай түрде анықталады:
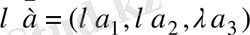
Ал
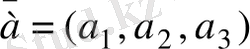 және
және
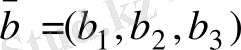 векторларының скаляр көбейтіндісі мынадай:
векторларының скаляр көбейтіндісі мынадай:
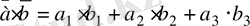
Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусына көбейтіндісіне тең шаманы айтады:
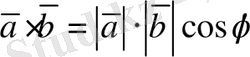
12. v векторды x, y, z, …, u векторларының сызықты комбинациясы, яғни
R сызықты кеңістіктің векторлары x, y, z, …, u болсын. Мынадай
v=
 x+
x+
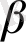 y+
y+
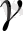 z+…+
z+…+
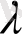 u
u
теңдікпен анықталған
v
векторы осы кеңістікте жатады, мұндағы
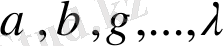 -нақты сандар. Осы
v
векторды
x, y, z, …, u
векторларының
сызықты комбинациясы
деп атайды.
-нақты сандар. Осы
v
векторды
x, y, z, …, u
векторларының
сызықты комбинациясы
деп атайды.
Айталық x, y, z, …, u векторларының сызықты комбинациясы 0 ноль вектор болсын, яғни
 x+
x+
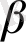 y+
y+
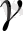 z+…+
z+…+
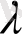 u= 0.
(1)
u= 0.
(1)
Анықтама.
(1) теңдік барлық
 =
=
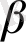 =
=
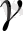 =…=
=…=
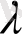 =
0 болған кезде ғана орындалса
х, y, z, …, u
векторлары
сызықты тәуелсіз
деп аталады. Ал егер (1) теңдік
=
0 болған кезде ғана орындалса
х, y, z, …, u
векторлары
сызықты тәуелсіз
деп аталады. Ал егер (1) теңдік
 ,
,
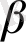 ,
,
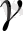 , …,
, …,
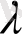 сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса
х, y, z, …, u
векторлары
сызықты тәуелді
деп аталады.
сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса
х, y, z, …, u
векторлары
сызықты тәуелді
деп аталады.
Мынадай тұжырымның дұрыстығына көз жеткізу қиын емес: Егер x, y, z, …, u векторлар сызықты тәуелді болса, онда бұл векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктеледі. Және керісінше, Егер x, y, z, …, u векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктелсе, онда бұл векторлар сызықты тәуелді болады. . Егер x, y, z, …, u векторларының ішінде ноль-вектор бар болса, онда бұл векторлар сызықты тәуелді болады. Шынында да, егер, мысалы, x=0 болса, онда (1) теңдік
 =
1,
=
1,
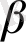 =
=
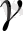 =…=
=…=
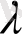 =0 болғанда орындалады.
=0 болғанда орындалады.
2.
Егер x, y, z, …, u векторларының қандай да бір бөлігі сызықты тәуелді болса, онда бұл векторлардың бәрі сызықты тәуелді болады.
Шынында да, мысалы,
y, z, …, u
векторлары сызықты тәуелді болсын десек
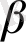 y+
y+
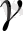 z+…+
z+…+
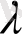 u=0
теңдік
u=0
теңдік
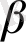 ,
,
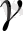 , …,
, …,
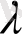 сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол
сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол
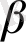 ,
,
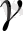 , …,
, …,
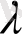 сандары және
сандары және
 =
0 санымен де орындалады.
=
0 санымен де орындалады.
13. Қандай векторлар жиынын базис деп аталады?
п өлшемді векторлық кеңістіктің п сызықты тәуелсіз векторларының жиыны базис деп аталады.
Мынадай тұжырымдар дұрыс болады:
1. Егер қандай да бір векторлар базис құрса, онда осы векторлардың координаталарынан құрылған анықтауыш нолден өзгеше болады.
2. п өлшемді векторлық кеңістіктің әр бір векторы базистік векторлардың сызықты комбинациясы арқылы жазылады және бұл жазу жалғыз болады.
Сонда, егер
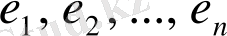 - кеңістіктің базисі болса, онда кез келген
x
- кеңістіктің базисі болса, онда кез келген
x
 R векторы жалғыз түрде былай жазылады:
R векторы жалғыз түрде былай жазылады:
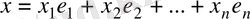 .
.
Демек
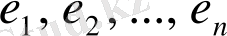 базисінде
х
векторы
базисінде
х
векторы
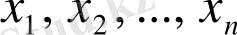 сандарымен жалғыз түрде анықталады.
сандарымен жалғыз түрде анықталады.
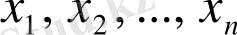 сандар
х
векторының осы базистегі
координаталары
деп аталады.
сандар
х
векторының осы базистегі
координаталары
деп аталады.
, x, y, z векторлары базис құрады екен.
Екінші тұжырым бойынша u векторы ( x, y, z ) базисте жіктеледі және ол жіктелу жалғыз болады:
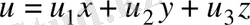 .
.
14. Жазықтықта
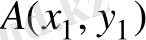 және
және
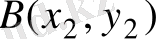 екі нүкте берілсін
. Екі нүкте ара қашықтығы.
Жазықтықта
екі нүкте берілсін
. Екі нүкте ара қашықтығы.
Жазықтықта
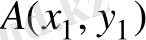 және
және
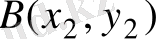 екі нүкте берілсін. Осы екі нүкте ара қашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:
екі нүкте берілсін. Осы екі нүкте ара қашықтығын, немесе АВ кесіндісінің ұзындығын, мына формуламен есептейді:
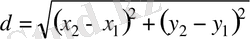 .
.
2. Кесіндіні берілген қатынаста бөлу
. Жазықтықта
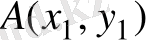 және
және
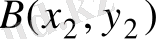 екі нүкте берілсін.
АВ
кесіндісін
АМ:МВ=
екі нүкте берілсін.
АВ
кесіндісін
АМ:МВ=
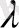 болатындай қатынаспен бөлетін
М(х, у)
нүктесінің координаталары мынадай формуламен есептелінеді:
болатындай қатынаспен бөлетін
М(х, у)
нүктесінің координаталары мынадай формуламен есептелінеді:
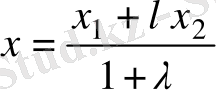 ,
,
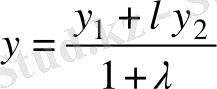 .
.
Дербес жағдайда, АВ кесіндісін тең екіге бөлу керек болса, яғни
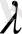 =1:1=1,
формула былай түрленеді:
=1:1=1,
формула былай түрленеді:
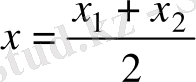 ,
,
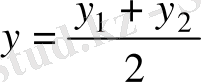 .
.
15. Оу осін
В(0; b)
нүктесінде қиып, Ох осімен
 (0<
(0<
 <
<
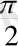 ) бұрыш жасасайтын жазықтықтағы
Оу осін
В(0; b)
нүктесінде қиып, Ох осімен
) бұрыш жасасайтын жазықтықтағы
Оу осін
В(0; b)
нүктесінде қиып, Ох осімен
 (0<
(0<
 <
<
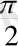 ) бұрыш жасасын. Түзу бойынан қандай да бір М(х, у) нүкте алайық. Түзудің Ох осімен жасаған
) бұрыш жасасын. Түзу бойынан қандай да бір М(х, у) нүкте алайық. Түзудің Ох осімен жасаған
 бұрышының тангенсін ВМК үшбұрышынан табамыз:
бұрышының тангенсін ВМК үшбұрышынан табамыз:
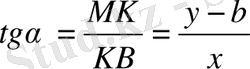 (1)
(1)
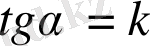 деп белгілеп,
түзудің бұрыштық коэффициенті
деп атау қабылданған. Сонымен:
деп белгілеп,
түзудің бұрыштық коэффициенті
деп атау қабылданған. Сонымен:
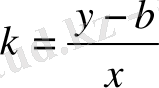 .
.
.
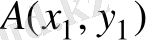 және
және
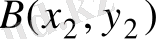 нүктелері берілсін.
АВ
түзуінің теңдеуін жазу үшін
А
нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:
нүктелері берілсін.
АВ
түзуінің теңдеуін жазу үшін
А
нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:
y =k(x - x 1 ) + y 1.
16.
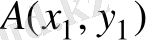 және
және
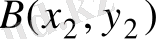 нүктелері арқылы өтетін түзу теңдеуін жазу керек.
нүктелері арқылы өтетін түзу теңдеуін жазу керек.
.
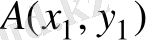 және
және
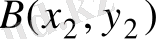 нүктелері берілсін
нүктелері берілсін
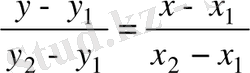
17. Түзудің “кесіндідегі” теңдеуінің жалпы түрі қандай?
 Түзудің “кесіндідегі” теңдеуі.
Түзу
Ох
осінен
а
-ға тең,
Оу
осінен
b
-ға тең кесінді қиып өтсін (8-сурет) . Түзу
А(а; 0)
және
В(0; b)
нүктелері арқылы өтеді деп, (5) теңдеуді қолданайық. Сонда түзу теңдеуі мынадай түрде жазылады:
Түзудің “кесіндідегі” теңдеуі.
Түзу
Ох
осінен
а
-ға тең,
Оу
осінен
b
-ға тең кесінді қиып өтсін (8-сурет) . Түзу
А(а; 0)
және
В(0; b)
нүктелері арқылы өтеді деп, (5) теңдеуді қолданайық. Сонда түзу теңдеуі мынадай түрде жазылады:
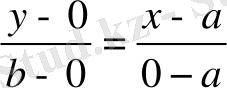
Енді ықшамдасақ, түзудің “кесіндідегі” теңдеуін аламыз:
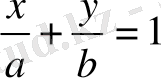
18. Түзулердің паральелдік және перпендикульярлық шарттарын жаз.
Екі түзудің параллелдік және перпендикулярлық шарты.
Егер екі түзу параллель болса, онда
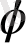 =0 болады да
tg
=0 болады да
tg
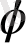 =0. Бұл жағдайда (7) формула мынадай түрге келеді:
k
2
-
k
1
= 0. Осыдан екі түзудің параллелдік шарты шығады:
=0. Бұл жағдайда (7) формула мынадай түрге келеді:
k
2
-
k
1
= 0. Осыдан екі түзудің параллелдік шарты шығады:
k 2 = k 1 , (8)
яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше.
Егер екі түзу перпендикуляр болса, онда
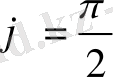 болады да,
болады да,
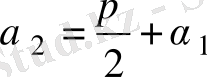 ,
,
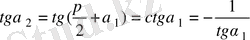 . Осыдан екі түзудің перпендикулярлық шарты шығады:
. Осыдан екі түзудің перпендикулярлық шарты шығады:
k
2
=
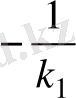 , (9)
, (9)
яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше.
19. Түзудің жалпы теңдеуін жаз.
Нүктеден түзуге дейінгі қашықтық. Тік бұрышты координаталар жүйесінде қандай да бір түзу Ах+Ву+С=0 және түзуден тыс жатқан нүкте М(х 0 , у 0 ) берілсін (10-сурет) .
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz