Шеннон энтропиясы: анықтамасы, қасиеттері және Хартли мен Колмогоров ұғымдарымен байланысы


Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:
Шеннон энтропиясы
Энтропия кайнардың көп болған сайын, көбірек дәреже берілетін кенеттіктің оларға хабарлаулардың ортада, әсіресе белгісізбен хабарлаулардың күтуі келеді.
Алғаш рет осы өлшемді (1. 7) Клод Шеннон ұсынды, оның жұмысының фундаменті «Математикалық негіздің байланыс теориясы» 1948 жылы жарияланды.
Кездейсоқ емес шамалаушы өлшем энтропиямен аталған болатын. (1. 7) формуланың түрі алдындағы алынған термодинамикалық жүйе энтропиясына арналған Вольцман айтылуының нәтижесімен сәйкес келеді.
Хартли өлшемімен Шеннона өлшем өзара байланысын қарап шығамыз, егер қайнарда тең h ықтималдық күй-жағдайларды мүмкін іске асырылған болса онда әрбір ықтималдық олардан
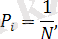 , мына өлшемді есепке ала Хартли қайнар анықтықсыздары
, мына өлшемді есепке ала Хартли қайнар анықтықсыздары
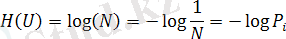 түсіндіруге болады, сан сияқты келуші хабардың бірді дискреттік хабарлау (сондықтан барлық қайнар хабарлаулары хабар тең ықтималдық сандары әрбірде олардан бірдей ) .
түсіндіруге болады, сан сияқты келуші хабардың бірді дискреттік хабарлау (сондықтан барлық қайнар хабарлаулары хабар тең ықтималдық сандары әрбірде олардан бірдей ) .
Шеннон энтропиясы - хабардың орта саны, бірде тең ықтималдық емес күй-жағдайларын ұстанады. Ол хабар қайнар статистикалық қасиеттерін ескеруге рұқсат етеді. Сонымен қатарға Хартли мен Шеннон қаралған өлшемдері хабар сандарының басқа анықтамаға жақын келеді.
Ең қызықтысы, Холмогоровтың ақпараттық концепциясы ең жаңа болып келді, оның негізгі тезисы энтропия анықтамасы негізінде хабар (1. 1. 7) саны Pi шабуылдаулары, өйткені ықтималдықпен байланыстырылады. Ықтималдық ұғымы мәні бар тек жеке актіде хабар бірліктерінің сан бұқаралық құбылыстарымен осымен орайлас және тап осы нәтижемен осымен орайлас назар таныстырушы, бұқаралық құбылыстардың ықтималдықтары арқылы айтылған болады. Мынау ішкі хабар ұстау қайшылығы, сүйенушінің алгоритмнің жалпы теорияларын таңдау концепциясы базада жалғасады.
Осыған сәйкес алгоритмдік энтропия Н ( u, z ) - жорамал ұзындық, жүйеліліктер 0 және 1 бағдарламалар түрінде жазылған, қайсы рұқсат етеді салу объекті u бола өз бұйрықта объекті z.
Сол уақытта негізгі хабар ұғымы ықтималдық теориясына айналдырусыз негізгі бола алады, және де дәл осылай, энтропия ұғымын және хабар санын дара объектілерге қатал қабылдауға болады.
Бірақ Шеннондық өлшем өз-өзімен қызықты емес, ал негіз сияқты қоса салынған байланыс технигінде мүмкіншіліктерді өзгерту және кеңейту туралы теориялар бар болу жорамалдар мүмкіндік беретін, және АТ қарауында жатады.
1. 2 Энтропия қасиеттері
1) Дискреттік ансамбльдің энтропиясы жағымсыз емес
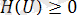
Теңдік нольге (=0) мүмкін оқиғада, қашан Р=1 ықтималдығымен жалғыз хабарлау бір қайнар генерациялайды, басқа хабарлаулардың ықтималдық оқиғасында нольге бірдей.
Мойындамау емес сәйкес, не хабар саны әрбір мүмкін хабарлаулар қайнар айқындарының (1. 5) сәйкестікте жағымсыз емес.
2) N- дискреттік қайнар әліпби көлемі, онда

Бүкіл хабарлау қайнары тең ықтималды болғанда ғана, теңдік орын алады.
Дәлелдеу үшін (1. 2. 2) теңсіздігін қарастырайық,
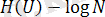 егер барлық хабарлау қайнары u
k
k=1:N оларға P(u
k
) ықтималдығымен сәйкес келсе, онда былай жазуға болады
егер барлық хабарлау қайнары u
k
k=1:N оларға P(u
k
) ықтималдығымен сәйкес келсе, онда былай жазуға болады
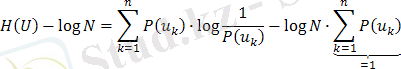
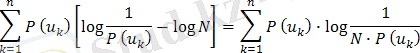
(1. 10)
Келесі дәлелдеулер үшін
 теңсіздікті қолданайық
теңсіздікті қолданайық


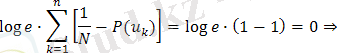
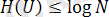
(1. 12)
Дәлелдеу керек осы еді.
Сәйкес (1. 2. 3)
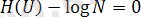 сол жағдайда,
сол жағдайда,
 тең болғанда(бұл теңдіктен шығада:
тең болғанда(бұл теңдіктен шығада:
 ) .
) .
Сонымен, максималды мүмкін N әліпби көлемді дискреттік қайнар энтропиясының мағынасы logN тең және оның барлық хабарлары тең ықтималды болғанда жетеді.
3) хабарлаулардың бірнеше - статистикалық қайнарлардың біріктіру энтропиясы негізгі қайнарлардың энтропия сомасымен бірдей - адетивтік энтропия қасиеті .
Жалпылықтарды жоғалтпай, u және z қараумен әліпби көлемдерімен N және M сәйкес біріктірулерді қанағаттандырамыз.
Екі u және z қайнарының бірігуі деп, (u*z) жалпы хабар қайнарын түсінеді, P( u i z j ) барлық мүмкін комбинациялары, u i - u қайнарының, z i - z қайнарының.
(1. 7) анықтамасына сәйкес жалпы қайнардың энтропиясы:

(1. 13)
Статистикалық u және z тәуелсіздігі жағдайында:

онда


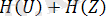
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz