Экономика мен басқаруда қолданылатын математикалық әдістер: тиімді шешімдер, сызықтық бағдарламалау және алгебралық тәсілдер


Мазмұны.
Кіріспе бөлім
Кіріспе . . . 3
Негізгі бөлім
1. 1 Тиімді шешім туралы ұғым . . . 6
1. 2 Алгебра және жоспарлау . . . . . 8
1. 3 Сызықтық емес теңдеулер жүйесінің теріс емес шешімін анықтау…… . . . 14
1. 4 Сызықтық бағдарламалау есебінің негізгі элементтері . . . 20
Қорытынды бөлім . . . 25
Пайдаланылған әдебиеттер . . . 26
Кіріспе.
Қазіргі қоғамның мәдениеті, білімділігі, ой өрісі және ой жүйесі дамыған кезеңде халық шаруашылығының кәсіпорындарының қандай түрі болмасын, оның экономикасын ұтымды басқаруда математикалық әдістер мен компьютерді кеңінен қолдану қажеттігі әркімге белгілі.
Математиканың экономикада және басқа ғылымдарда кеңінен қолданылуы осы ілімнің өзіне тәне ерекшелігі болып табылады. Егер оның осы ерекшелігі түбегейлі экономикалық талдаумен біріктіре отырып пайдаланылса, онда өндірістік жұмыстарды тиімді ұйымдастыруда және басқаруда, яғни әр істен ұтымды табыс табу жолдарында математикалық әдістемелеерді қолдану - бүгінгі таңдағы ең қажетті істің бірі.
Экономикалық жүйелердің әртүрлі деңгейлерінде кездесетін жоспарлау, басқару, шектелген ресурстарды бөлу, өндірістік процесстерді талдау, күрделі обьектілерді жобалау сияқты есептердің ұтымды және оптимизациялық шешімдерін табу - табиғи және ғылыми - техникалық прогресс қажеттіліктерінен туған мәселе.
Экономикада қолданылатын математикалық әдістердің жиынын белгілеу үшін әртүрлі атаулар қолданылды. Алғашқысында мұндай жиын экономикалық кибернетика деп аталды, кейіннен операцияларды (әрекеттерді) зерттеу, одан кейін экономикалық - математикалық әдістер деп аталып жүр.
Экономикада және басқарудағы есептерді шығаруға арналған, қазіргі кездегі математикалық әдістердің аппараттары, өз алдына дамыған ғылымға және қолданбалы аймаққа айналды. Дегенмен де, қолданбалы математикалық оқып - үйренуде, күнделікті өмірде жиі қолдануды қалыптастыруда көптеген қиыншылықтар мен түсінбеушіліктер кездеседі. Халық шаруашылығының көптеген мамандары математикалық әдістердің көкейтестілік мәнісін әлі де болса дұрыс түсінбейді де, олардың қажеттілігін және осы әдістер арқылы әр істе кереметтей нәтижеге жетуге болатынын сезінбейді. Осы айтылғанның дәлелі ретінде мынадай мәселеге көңіл аударайық. Мысалға, кейінгі кезде республикамызда көптеген жоғары оқу орындарында қолданбалы математикалық пәндер халық шаруашылығының әр саласының мамандарын дайындауға арналған мемлекеттік стандарттарға бірде енгізіліп, бірде алынып тасталынады немесе өте аз сағат бөлініп, факультативтік пән ретінде жүргізіледі. Сонымен қатар қазіргі компьютерлік техниканың мүмкіншілігі өсуіне және көптеген қолданбалы математикалық әдістер бойынша компьютерге арналған қолданбалы бағдарламалар пакеттері жасалуына байланысты, олардың математикалық аппараттарын, яғни есепті шығару алгоритмдерін оқып, терең түсіну қажет емес деген сөз де жиі айтылады. Әрине, математикалық әдістерге мұндай қөзқараспен қоғамымызда жуық арада табысты өзгерістерге жету мүмкін емес.
Оптимизациялық есептердің қойылым түрлері әртүрлі математикалық әдістерді тиімді пайдалануға мүмкіндік береді. Математикалық әдістерді пайдалану үшін, ең алдымен, тиімді шешімін таппақшы болған есептің өзінің қойылымын жазуымыз қажет. Математикалық қойылымда берілген ресурстар, өндірістік технология, қорытынды шешімдер және олардың арасындағы байланыстар математикалық өрнектер, теңсіздіктер арқылы көрсетіледі.
Өмірде өзінің кәсібі бойынша әртүрлі құралдарды, жұмыстың сипаты бойынша қолдана алатын адам, әмбебап тәсілдерді меңгерген адамға қарағанда, артық нәтижеге жетеді. Мысалға, бірде ойша немесе қағазға жазып, ал үшінші жағдайда - компьютер арқылы, төртіншіде - арнайы бағдарлама арқылы оптимизациялық есептеулер жүргізген тиімді болуы мүмкін. Сондықтан да әмбебап және жекеленген тәсілдерді білу және қолдана алу, тез және оңай қойылған мақсатқа жеткізеді. Сөйтіп тәжірибелік есептерді математикалық әдістермен шығару алгоритмдерін білу және қолдана алу есептің мәнісін, сонымен қатар мағынасын терең түсініп, ұғуға ықпал жасайды.
Шындығында, қазіргі компьютердің мүмкіншіліктері және оларға арналған бағдарламалық пакеттер, тәжірибелік есептерді шығарудағы мамандардың жұмысын: есепті қойып, оның математикалық формалдау (тәртіптеп, реттеп жазу) әрекеттерін жасағаннан кейін, оны шешу жұмысын тек компьютердегі қолданбалы бағдарламалар пакетін пайдалануына ауыстырады.
Бұл жерде есепте қойылған мәселелерді формалдау (тәртіптеп, реттеп жазу), үлкен қабілеттілікті және көп білімділікті, сонымен қатар қойылған есепті қандай математикалық әдіспен шығаруға болады, ол үшін қандай мәліметтер қажет, қандай талаптар орындалуға тиісті екенін анықтауды қажет етеді.
Математика сипаты және мәселесі қаралатын обьектінің өзімен емес, оның математикалық моделімен жұмыс істейді. Сондықтан қойылған есептің жағдайын математикалық формалдау (тәртіптеп, реттеп жазу) дегеніміз - есепті шешу жолындағы 50% жетістік. Есепті реттеудің қиыншылығы, оны тым ұсақ бөлшектерге бөлмей, маңызды және мәнді жағдайларын сақтап, белгілі бір математикалық әдіспен шеше алатындай, модельдің түрін қалыптастыруда.
Есепті қойып, реттеп - тәртіптеп жазуда, ізделінетін айнымалыларды тағайындау, шектеулі ресурстарды өрнектеу, шығарылған варианттардың оптималдылығын бағалау - бірінші кезекте орындалатын мәселелер. Оптимизациялық есептердің қойылған мақсатқа жеткендегі табылған нәтижелері - басқару шешімдерін қабылдау үшін, негізгі көрсеткіш. Сондықтан талданылатын құбылыстың математикалық моделі нақтылы және шындыққа өте жақын болған сайын басқару шешімі де нәтижелі.
Қазіргі экономика, математикалық бағдарламалар жасау пәнін құрайтын арнайы оптималдау әдістерін: ойындар теориясы, торлық жоспарлау, массаға қызмет ету теориясы және басқа да қолданбалы ғылымдары пайдаланады. Сөйтіп, микроэкономика, макроэкономика және қолданбалы математика пәндерінің дамуы, негізі, математикалық бағдарлама жасау, ойындар теориясы және математикалық статистика ілімдерінен басталады.
1. 1 Тиімді шешім туралы ұғым.
Тиімді шешім табу (ең үлкен немесе ең кіші) мәселесімен ерте заманнан бастап көптеген оқымысты ғалымдар айналысты, сонымен қатар олар табылған әдістерді әртүрлі ғылым салаларында, оның ішінде: математикада, геометрияда, механикада, физикада және т. б. ілімдерде қолдана білді.
Мысалы, атақты ғалым Евклид берілген нүктемен берілген шардың қиылысуынан пайда болатын кесінділердің ең үлкен және ең кіші ұзындықтарын табу жолдарын анықтады. Тиімді шешуін табуға арналған есептер тәжірибе жүзінде өте көп. Бұл есептердің қатарына: берілген қорды дұрыс пайдалана отырып, өндірісті қалай ұйымдастырғанда өнім өндіруі көбейеді, жол қатынасы жұмыстарының шығынын қалай азайтуға болады, тиімді рацион жасау қалай жүзеге асырылады және т. с. с есептер жатады. Бұл айтылған есептердің жоғарыда келтірілген Евклид есебінен көптеген айырмашылықтары бар. Сондықтан бұл есептерді шешуге арналған өзгеше әдістер болуы қажет. Қазіргі таңда осындай әдістердің бірнеше түрі тәжірибеде қолданылуда. Осындай қолданбалы математикалық әдістер біріктіріліп, математикалық бағдарламалау пәнін құрайды.
Сонымен тиімді шешім деп қандай шешімді айтамыз? Бұл сұраққа жауап беру үшін ең қарапайым мәселеден бастайық. “Таңертеңгі киім киіну әрекетін бағдарламалау” есебін қарастырайық. Адам ерте тұрып киінгенде киімді әртүрлі тәртіппен киюі мүмкін. Біреулері ең алдымен шөлкейін, одан соң шалбар, көйлек т. б. кие бастайды. Сонымен ешкім де киімді қай тәртіпте киіну тиімді екендігін ойламайды. Алайда киім киюдің де тәртібі болады, олардың ішінде қарастырмайтын жағдай да болуы мүмкін. Мысалы, көйлекті костюмнің сыртынан, шөлкейді аяқкиімнің сыртынан киюге болмайды емес пе. Міне, осы сияқты қолданылмайтын жағдайларды алып тастағанның өзінде, киім киюдің де көптеген жағдайлары бар, ал бізге осы жағдайдың ішінен ең тиімдісін тауып алу қажет.
Қалай болғанмен де, есепті шешу варианттары аз болмайды, міне, осылардың ішінен ең тиімді (аз уақыт жұмсалатын) шешімді табуға тура келеді. Ол үшін біз алдымен есептің мақсатын, одан кейін осы мақсат орындалу үшін қандай шарттар қажет болатындығын анықтап алуымыз қажет. Алдымызға мақсат қоймай тұрып, тиімді шешім табу мүмкін емес. Біздің жағдайымызда алға қойған мақсатымыз - қойылған шарттарды бұзбай, қай тәртіппен киінгенде, киінуге ең аз уақыт кететіндігін анықтау. Бұл мақсатты математика тілінде жазу үшін, мақсат функциясы деген ұғым енгізуге тура келеді. Сонымен әр түрлі вариантқа сәйкес мақсат функциясының мәнін тауып, оларды салыстыра отырып, ішінен ең тиімдісін табу қажет. Бұл сияқты біртіндеп таңдау әдісі, варианттардың өте көптігіне байланысты, қойылған мақсатқа жету ғана тиімді әдіс емес және ол ең тиімді шешім болмауы да мүмкін. Сондықтан есепті математикалық бағдарламалау әдісімен шешу қажет. Өйткені бұл салада табылған шешімнің ең тиімді шешім беретіндігі математика түрінде дәлелденген.
Есептің бірнеше шешімдері (ең кем дегенде екеу және одан да көп) болған жағдайда ғана, берілген есеп математикалық бағдарламалау есебіне жатады.
Есепті толық шешу үшін, тек мақсат функциясының беріліп қана қойылуы жеткіліксіз. Мақсатты орындау үшін орындалатын шарттар немесе шектеулер болуы керек. Мұны математика тілінде есептің анықталу аймағы немесе есепке қойылатын шарттар дейді. Сөйтіп тиімді шешім табу үшін, алдымен мақсат функциясы және оның анықталу аймағы, басқаша айтқанда, сол мақсатқа орай шешім табу шарттары берілуі қажет.
Қойылған шарттарды орындайтын мақсат функциясының ең үлкен (ең кіші) мәнін берілген есептің (мақсаттың) тиімді шешімі дейді.
1. 2 Алгебра және жоспарлау.
Жоғарыда біз тиімді шешімді табу үшін алдымен алдымызға мақсат қою қажет дедік. Ал ол (мақсат функциясы) берілген жағдайды немесе шарттарды қанағаттандыруы керек. Мақсат функциясына және шарттарға енген белгісіздер өте көп және үлкен дәрежелі болуы мүмкін. Егер есепке енген белгісіздердің дәреже көрсеткіші бірден артпаса, мұндай есептерді сызықтық алгебра есептеріне жатқызады. Мұндай жағдайда есептің берілген шарттары сызықтық теңдеу немесе теңсіздіктер түрінде беріледі. Осындай есептерді қарсатыру үшін, алдымен сызықтық алгебраның кейбір түсініктеріне тоқталайық.
Сызықтық алгебранаң жоспарлау жұмыстарында қолдану жолдарын қарастырайық.
1-мысал. Айталық, цех екі түрлі трансформатор жасайды екен дейік. І-ші түрдегі трансформаторды жасау үшін 6 кг трансформаторлық темір, 4 кг сым, ал ІІ-ші түрдегі трансформаторды жасау үшін 5 кг трансформаторлық темір, 3 кг сым қажет болсын. Егер трансформатор темірінің қолда бар қоры q 1 , ал сымның қоры q 2 болса, осы қорларды пайдаланып, әртүрлі трансформатор-лардың қаншауын жасауға болатындығын анықтайтын формуланы табу қажет.
Бұл есепті шешу үшін, ең алдымен алгебралық теңдеулер жүйесін құрайық. Ол үшін І-ші түрдегі белгісіз трансформатордың санын Х 1 деп, ал ІІ-ші түрдегінің санын Х 2 деп белгілеп аламыз.
Есептің шарты бойынша, егер бірінші түрдегі бір трансформаторға 6 кг темір қажет болса, онда Х 1 трансформаторға 6Х 1 кг темір, ал екінші түрдегі Х 2 дана трансформаторға 5Х 2 кг темір қажет болады. Ендеше, І-ші және ІІ-ші түрдегі трансформаторларды Х 1 және Х 2 данадан жасау үшін қажетті темір көлемі қолда бар трансформатор темірімен тең болуы керек. Демек, төмендегідей теңдеу құрамыз:
6Х 1 + 5Х 2 = q 1
Осы сияқты сым үшін де теңдеу құруға болады:
4Х 1 +3Х 2 = q 2.
Сонымен біз екі белгісізі бар екі алгебралық теңдеу алдық:
6Х 1 + 5Х 2 = q 1 (1. 1)
4Х 1 +3Х 2 = q 2
.
Алгебра тілінде мұндағы берілген 6, 5, 4, 3 сандары белгісіз Х 1 және Х 2 - лердің коэффициенттері деп, ал q 1 , q 2 бос мүшелер деп аталады. Енді (1. 1) теңдеулер жүйесін пайдалана отырып, Х 1 және Х 2 табуға арналған формула табуды қарастырайық. Ең алдымен, әрбір оқырман білетін қарапайым әдістен бастайық. Ол үшін І-ші теңдеудегі Х 1 - ді бос мүше q 1 және q 2 арқылы өрнектелік:
6Х
1
= q
1
- 5X
2
немесе Х
1
=
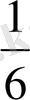 q
1
-
q
1
-
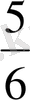 Equation. 3 X
2
(1. 2)
Equation. 3 X
2
(1. 2)
Табылған Х 1 -дің мәнін ІІ-теңдеуге апарып қойсақ, ІІ-теңдеудегі Х 2 - q 1 және q 2 арқылы өрнектеледі:
4
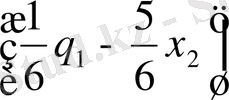 + 3Х
2
= q
2
(1. 3)
+ 3Х
2
= q
2
(1. 3)
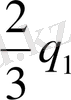 -
-
 X
2
= q
2
X
2
= q
2
Сонымен төмендегідей екі теңдеу аламыз:
x
1
=
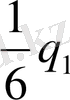 -
-
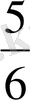 x
2,
x
2,
q
2
=
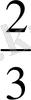 q
1
-
q
1
-
 x
2
(1. 4)
x
2
(1. 4)
Осы жүйедегі теңдеудің екіншісінен Х 2 тауып, біріншісіне қойсақ, іздеп отырған Х 1 және Х 2 - лерді табатын формула аламыз:
1/3X 2 =2/3q 1 - q 2 немесе X 2 =2q 1 - 3q 2 ,
X 1 = 1/6q 1 - 5/6(2q 1 - 3q 2 ) = -3/2q 1 + 5/2q 2 = 5/2q 2 - 3/2q 1 ,
Яғни: X 2 =2q 1 - 3q 2 ,
X 1 =5/2q 2 - 3/2q 1 . (1. 5)
(1. 5) теңдеуде Х 1 және Х 2 бос мүшелер q 1 және q 2 арқылы өрнектелді, демек бұл жүйе Х 1 және Х 2 белгісіздерін табуға арналған формула болып есептеледі. Егер біз қолда бар темір q 1 және сым q 2 қорларын білсек, онда жасалатын трансформаторлар саны Х 1 және Х 2 таба аламыз.
Айталық, темір қоры q
1
=190 кг, сым қоры q
2
=120 кг болсын, онда бұл қорларды пайдалана отырып, І-ші түрдегі трансформатордан: Х
1
=
 120кг -
120кг -
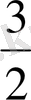 190=560-395=300-285=15 дана, ал ІІ-ші түрдегі трансформатордан: Х
2
=2x190-3x120=380-360=20 дана жасалатынын оңай табамыз.
190=560-395=300-285=15 дана, ал ІІ-ші түрдегі трансформатордан: Х
2
=2x190-3x120=380-360=20 дана жасалатынын оңай табамыз.
Мұндағы ескерте кететін бір жай: жалпы жағдайда алгебралық теңдеулер шешкенде, берілген белгісіздердің коэффициенттеріне және бос мүшенің мәндеріне тәуелді белгісіздердің мәндері оң санда, теріс санда, бөлшек немесе бүтін санда болуы мүмкін. Қарастырып отырған есепте Х 1 және Х 2 мәндері тек оң және бүтін болуы керек. Трансформаторлардың саны теріс болуы мүмкін емес, ол тек нөл немесе нөлден жоғары бүтін сан болуға тиіс. Сондықтан есепті шешуде осындай мәселелерге көңіл аударған жөн.
Енді бұл есептің q 1 =190 кг, q 2 =120 кг болғанда, шешімін график түрінде қарастыралық. Ол үшін тікбұрышты координат жүйесін алып, оның жатық өсін (абцисса) Х 1 арқылы, ал тік өсін (ордината) Х 2 деп белгілейік. Алдымен І-ші теңдеудің графигін сызайық, ол үшін бірінші теңдеудегі Х 1 =0 десек, 5X 2 =190 шығады, осыдан Х 1 =31, 6 шығады. Енді табылған нүктелерді графикке түсірейік (1. 1 - сурет ) .
Геометрияның кез келген екі нүкте арқылы тек бір ғана түзу жүргізуге болады деген теоремасын пайдалана отырып, І-ші теңдеудің графигін аламыз. Сол сияқты екінші теңдеудің графигін табуға болады (Х 1 =30, X 2 =40) .
Екі графиктің (түзу сызықтың) қиылысу нүктесінің координаты М(15, 20) есептің шешуін береді.
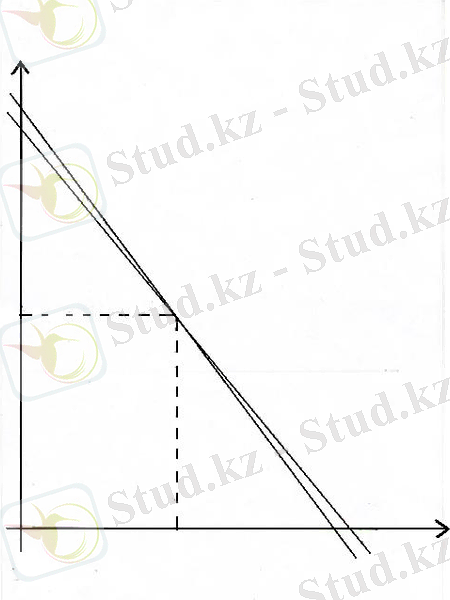 4Х
1
+3Х
2
=120 (0:40) (30:0)
4Х
1
+3Х
2
=120 (0:40) (30:0)
6Х 1 +5Х 2 =190 (0:38) (31, 6:0)
Х 2
І
38
20
0 15 31, 6 Х 1
1. 1 - сурет
2 - мысал. Мал фермасында малды жемдеуде апталық рацион жыл мезгіліне байланысты әртүрлі заттардың (витаминдердің) құрамынан тұратындығы белгілі. Айталық, әртүрлі жемнің құрамында үш түрлі жұғымды (А, В, С) бар болсын. Қарастырылып отырған жемнің 1 өлшем бірлігінде олардың қанша мөлшерде болатыны мына кестеде келтірілсін.
Мұндағы q 1 , q 2 және q 3 бір тәулікте бір бас малға қажетті әртүрлі заттардың мөлшері. Жоғарыда берілгендерді пайдалана отырып, бір тәулік рационға керекті жемдердің көлемін анықтайтын формула табу керек.
Шешуі: Рациондағы бірінші түрдегі жемнің мөлшерін Х 1 өлшем бірлікте деп, екінші түрдегі жемнің мөлшерін Х 2 , ал үшінші түрдегі жемнің мөлшерін Х 3 деп белгілейік.
Бірінші түрдегі жемнің 1 өлшем бірлігінде А заты 6 өлшем бірлік те болса, онда Х 1 өлшемінде - 6Х 1 болады, екінші жемде А заты 3 өлшем бірлікте болғандықтан, Х 2 өлшемінде - 3Х 2 , ал үшінші түрдегі жемде 2Х 3 өлшемді А заты бар, ендеше, бұлардың қосындысы сол заттың керекті мөлшеріне тең болуы керек, яғни:
6Х 1 + 3Х 2 + 2Х 3 = q 1 ,
Сол сияқты қалған заттар үшін де теңдеу құрсақ, олар былай болар еді:
3Х 1 + 4Х 2 + Х 3 = q 2 ,
Х 1 + 2Х 2 + 2Х 3 = q 3 .
Сонымен біз есепті шешуге қажетті үш белгісізі бар үш теңдеулер жүйесін таптық:
6Х 1 + 3Х 2 + 2Х 3 = q 1 ,
3Х 1 + 4Х 2 + Х 3 = q 2 , (1. 6)
Х 1 + 2Х 2 + 2Х 3 = q 3 .
Енді керекті формуланы табу үшін, Х 1 , Х 2 және Х 3 белгісіздерін, бос мүше q 1 , q 2 және q 3 - лер арқылы өрнектеу керек.
Ол үшін (1. 6) жүйенің 3-ші теңдеуінен Х 1 - ді тауып, қалған І және ІІ - теңдеулердегі Х 1 - дің орнына апарып қойсақ:
Х 1 = q 3 - 2Х 2 - 2Х 3 ,
6(q 3 - 2Х 2 - 2Х 3 ) + 3Х 2 + 2Х 3 = q 1 ,
3(q 3 - 2Х 2 - 2Х 3 ) + 4Х 2 + Х 3 = q 2 ,
шығады. Немесе:
Х 1 = q 3 - 2Х 2 - 2Х 3 ,
q 1 = 6q 3 - 9X 2 - 10X 3 (1. 7)
q 2 = 3q 3 - 2X 2 - 5X 3
(1. 7) жүйенің 3-ші теңдеуінен Х 2 -ні тауып, І және ІІ - ші теңдеулердегі Х 2 орындарына қойсақ:
Х
2
=
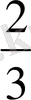 q
3
-
q
3
-
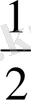 q
2
-
q
2
-
 X
3
X
3
X 1 = -2q 3 +q 2 +3X 3 (1. 8)
q
1
= -
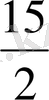 q
3
+
q
3
+
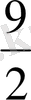 q
2
+
q
2
+
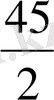 X
3
X
3
Шығады.
(1. 8) жүйенің соңғы теңдеуінен Х 3 - ті тауып, І және ІІ - теңдеулердегі Х 3 - тің орындарына қойсақ, іздеп отырған формуланы табамыз. Яғни:
алдыңғы алгебралық әдіспен есептегенде есептің шешімі
X
1
=
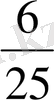 q
1
-
q
1
-
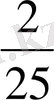 q
2
-
q
2
-
 q
3
,
q
3
,
Х
2
=
 q
1
+
q
1
+
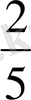 q
2
, (1. 9)
q
2
, (1. 9)
Х
3
=
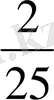 q
1
-
q
1
-
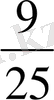 q
2
+
q
2
+
 q
3
q
3
Бұл теңдеулер жүйесінде белгісіз жемнің көлемдері Х 1 , Х 2 және Х 3 - тер бос мүше q 1 , q 2 және q 3 бір тәулікке керекті жағымды заттар арқылы өрнектеледі. Демек, (1. 9) жүйе іздеп отырған формуламызды береді, былайша айтқанда, бұл жүйе арқылы бір тәулікке керекті жемдердің мөлшерін есептеп табуға болады. Мысалы, бір тәулікке қажетті А жұғымды затының шамасы q 1 =96 өлшем бірліктей В затының шамасы q 2 = 68 өлшем бірліктей және С затының шамасы q 3 = 38 өлшем бірліктей дейік те, керекті жемдердің мөлшерлерін (1. 9) формула бойынша есептейік:
Бірінші түрдегі жем
Х 1 = 6/25*96 - 2/25*65 - 1/5*38 = 10 өлшем бірлік;
Екінші түрдегі жем
Х 2 = -1/5*69 + 2/5*68 = 8 өлшем бірлік;
Х 3 = 2/25*96 - 9/25*68+3/5*38 = 6 өлшем бірлік.
Сонымен бұл екі мысалдарды шешкенде, белгісіздерді орнына қою әдісін пайдаланып, бос мүше арқылы өрнектедік. Басқа да әдістермен (1. 1) теңдеу (1. 6) теңдеу түріне және (1. 5) теңдеу (1. 9) теңдеу түріне айналдырылып, нәтижесінде қойылған мақсатқа байланысты тұжырымдалған әмбебап формула құрылады.
Алдыңғы тақырыптардағы сызықтық бағдарламалау есептерін шешу алгоритмдерін жетік түсініп ұғуға дайындық жасау мақсатында алгебрада кездесетін біраз түсініктерге тоқталайық.
1. 3 Сызықтық емес теңдеулер жүйесінің теріс емес шешімін анықтау.
Қазіргі кезде сызықтық алгебралық теңдеулер жүйесін әртүрлі дәрежеде қолданбайтын ғылыми салалар жоқ. Сызықтық теңдеулер жүйелері экономикалық зерттеулерде, оптималдық экономикалық есептерде қалыптастырып, тәжірибе жүзінде шығаруда айрықша қолданылады. Бұл жерде сызықтық бағдарламалау курсының әмбебап симплекс әдісі сызықтық теңдеулер жүйесін шешу әдістеріне және оның ішінде айнымалылардың теріс емес мәндерін ерекше бөлектеп шешетін әдістеріне негізделгені туралы алдын ала айтып кеткеніміз жөн. Сондықтан да осы бөлім, симплекс әдісінің алгоритмінің теориялық негізін баяндауға дайындық жасауға арналған.
Сызықтық теңдеулер жүйесін шешу үшін қолданылатын орнына қою (айнымалыларды бірінен кейін бірін қысқарту) тәсілі және алгебралық қосу тәсілі, сызықтық теңдеулер жүйесінің қасиеттері, сонымен қатар жүйедегі теңдеулердің біріккендігі немесе бірікпегендігі туралы анықтаулар алгебра курсының мектептік бағдарламасында қарастырылады.
Сызықтық теңдеулер жүйесі матрица қалпына келтіріліп, әртүрлі әдістермен (мысалға, Крамер әдісі, Гаусс әдісі және т. б. ) көптеген орыс тілінде жазылған әдебиеттерде келтіріледі. Солардың ішінде сызықтық теңдеулер жүйесі кесте құрып шығару жолдары, сызықтық бағдарламалау курсының симплекс әдісінің алгоритмінің негізін құрайды.
Кесте әдісі.
Кесте әдісінің технологиясын түсіндіру үшін, алдыңғы 1. 2 - тақырыпта көрсетілген екінші мысалдың теңдеулер жүйесін қарастырайық:
6Х 1 + 3Х 2 + 2Х 3 = q 1 ,
3Х 1 + 4Х 2 + Х 3 = q 2 ,
Х 1 + 2Х 2 + 2Х 3 = q 3 .
Бұл теңдеулер жүйесін мына төменгі кесте түрінде жазайық.
1. 1 - кесте
Х 1 Х 2 Х 3
q 1 =
q 2 =
q 3 =
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz