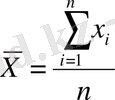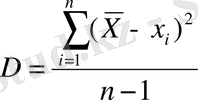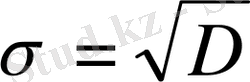Биологиялық статистика негіздері оқу-әдістемелік нұсқау

Пән: Статистика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 60 бет
Таңдаулыға:

ҚАЗАҚСТАН РЕСПУБЛИКАСЫНЫҢ ДЕНСАУЛЫҚ САҚТАУ МИНИСТРЛІГІ
ҚАРАҒАНДЫ МЕМЛЕКЕТТІК МЕДИЦИНА АКАДЕМИЯСЫ

Б.К. Койчубеков, А.С. Букеева
биологиялық статистика негіздері
Оқу-әдістемелік нұсқау

Қарағанды, 2008

ПІКІР БЕРУШІЛЕР:

Ж.Т.Бакеев – ҚММА медициналық биофизика және информатика кафедрасының
доценті, м.ғ.к.;
А.З. Муратова – оқу-әдістемелік орталықтың бастығы, б.ғ.к.

Койчубеков Б.К., Букеева А.С. Биологиялық статистика негіздері. - Оқу-
әдістемелік нұсқау. - Қарағанды. – 2008 ж. - 50 б.

Оқу-әдістемелік нұсқауда әдетте медициналық және бтологиялық
зерттеулерде қолданылатын негізгі анықтамалар және статистикалық
процедуралар, нақты есептердің шешімі келтірілген. Өздігінен тексеру үшін
оқырмандар қосымшадағы есептер мен тестілік сұрақтарды қолдана алады.
Нұсқау медициналық оқу орындарының студенттеріне арналған.
ҚММА Әдістемелік кеңесінде талқыланған және келісілген
№ ___ Хаттама _______________ 200__ ж.
ҚММА Ғылыми кеңесімен бекітілген және ұсынылған
№ ___ Хаттама _______________ 200__ ж.

© Б.К. Койчубеков, А.С. Букеева, 2008 ж.

КІРІСПЕ

Қазіргі кезде сәйкес заңдылықтарды математикалық түрде жазуға тырысу
білімнің барлық салаларына таралды, сонымен қатар биология мен медицинаға
да. Көптеген медициналық-биологиялық құбылыстарға жиынтықтарды зерттеу
кезінде анықталатын статистикалық заңдылықтар тән. Осы жағдай математикалық-
статистикалық әдістерді қолдануды анықтаған маңызды жағдай еді.
Осылайша,көптеген экологиялық, генетикалық, цитологиялық, микробиологиялық,
фармакологиялық және басқа құбылыстар – табиғаты жағынан көп көлемді болып
табылады.
Клиникалық зерттеулерді өткізуге қатысты қарастырсақ, математикалық
статистика мақсат қойғанда, рандомизация әдістерін таңдағанда,
статистикалық мәнді қорытынды алу үшін қажетті пациенттер санын анықтауда,
алынған нәтижелерді талдау өткізгенде көмектеседі. Бұл құрал статистикалық
талдаудың негіздерін түсінуге көмектеседі, және де біз бұл құрал
студенттерді ғана емес, сонымен қатар статистикада өз ағаттықтарын жабуға
кіріскендердің барлығына көмек болады деген сенімдеміз.

СТАТИСТИКАЛЫҚ МӘЛІМЕТТЕРДІҢ ТИПТЕРІ

Кез келген биообъект қандай да бір белгілермен сипатталады. Бұл
сипаттарды өлшеу кезінде статистикалық мәліметтер алынады. Белгілер сандық
және сапалық болады. Сандық белгілердің мәндері үздіксіз (мысалы, салмақ,
бой, артерия қысымы) немесе дискретті (мысалы, пульс, балалар саны, түған
жылы) болу мүмкін.
Сапалық белгілер мәліметтердің түріне байланысты номиналды
(классификациялық) және ординалды (қатарлы) деп бөлінеді.
Номиналды шкалада өлшенетін белгі алдын-ала орнатылған градациялардың
шекті санының бір мәнін қабылдайды. Мысалдар: жынысы (ер, әйел), көздің
түсі (көгілдір, қара, қоңыр, жасыл), жануарлар жіктелуі және т.с.с.
Номинальды шкалада өлшенетін статистикалық мәліметтер, осы немесе басқа
градациялық белгілердің пайда болатын жиіліктері көрінетін кестелер түрінде
көрсетіледі. Номинальды мәліметтер социологиялық сұрауларды өңдеген кезінде
жиі пайда болады. Мысалы: белгілі бір сырқатта кездесетін белгілі бір
белгілердің жиілігі туралы сұрақ қызығушылық тудыруы мүмкін.
Ординалды шкалада өлшенетін сапалық белгілердің мәндері реттелген
болады.
Мысалдар: тесттік баллдар және мектеп бағалары (1,2, 3, 4, 5), өмір
жағдайының сапасы (нашар, орташа, жақсы, өте жақсы), температура (қалыпты,
қызуы көтерілген, жоғары, өте жоғары және т. б.).
Ординалды шкалада өлшенетін белгілер үшін қосып – алынатын
операциялардың ешқандай мағынасы жоқ..Мысалы: емтиханды беске тапсырған
студент статистика бойынша осы пәннен төртке тапсырған студентке
қарағанда бір бірлікке жоғары біледі деп айтуға болмайды. Себебі білімді
өлшейтін өлшем бірлік болмайды. Бірақ бірінші студент екіншісіне қарағанда
статистиканы жақсы біледі деп айтуға болады.
Ординалды белгілердің мәндерін сандық формада көрсету үшін келесі әдіс
қолданады. Белгілердің барлық мәндері өсу тәртібімен қатар түрінде
жазылады. Әрбір мәнге қатардағы номерге тең болатын сәйкес натурал сан
қойылады. Бұл санды ранг деп атайды. Мысалы: өмірдің сапалық жағдайы
(жаман, қанағаттанарлық, жақсы, өте жақсы) рангтармен көрсетіледі 1, 2, 3,
4. Рангтар түрінде көрсетілген ординалды белгілер үшін белгілер
жақындығының дәрежесін өлшеуге (мысалы: рангты корреляция), тарамдалу түрі
болжамды тексеруге және дисперсионды анализ жүргізуге мүмкіндік беретін
арнайы статистикалық әдістер жоспарланған.
Номиналды шкалада көрсетілген мәліметтер үшін қосу және алу
операциялары да анықталмаған. Бұл мәліметтер (ординалды белгілерге
қарағанда) реттелуге келмейді, сондықтан рангілер көмегімен сандық түрге
келтірілген. Арнайы статистикалық әдістерді қолдана отырып, белгілер
тәуелсіздігі туралы болжамды және екі не одан да көп таңдаманың бір түрге
қатысы туралы болжамды тексеруге болады.
Зерттелетін объектілердің барлық жиынтығы генеральды жиынтық деп
аталады. Егер бұл жиынтықта элементтердің саны аз болса, онда генеральды
жиынтықты толық зерттеуге мүмкіндік бар. Бірақ көп жағдайда генеральды
жиынтықта элементтер саны өте көп болғандықтан, немесе оның элементтеріне
жету қиындық туғызса, немесе басқа жағдайлардан генеральды жиынтықтың бір
бөлігі (таңдама) ғана зерттеледі.
Таңдама зерттеу нәтижелері нақты ықтималдық үлеспен барлық генеральды
жиынтыққа таралады.
Бұл жағдайда генеральды жиынтықтың негізгі сипаттамалары таңдама
бойынша бағаланады (яғни жуықтап анықталады). Сәйкес статистикалар таңдама
орташа, таңдама дисперсия және т.б. деп аталады.
Таңдама генеральды жиынтық туралы дұрыс, бұрмаланбаған көрініс беру
керек, немесе репрезентативті болу керек. Мысалы, әлеуметтік-экономикалық
жағдайы жақсы аймақты зерттеп, ішек инфекциясы ауруы туралы жорамалдауға
болмайды.
Егер генеральды жиынтықтың қасиеттері алдын-ала белгілі болмаса, онда
қарапайым кездейсоқ таңдау қолдану керек. Бұл дегеніміз – генеральды
жиынтықтың барлық элементтердің таңдамаға түсу ықтималдықтары бірдей болу
керек.
Мысалы, университет студенттерінен қандай да бір мәселе бойынша сұрау
өткізгенде бірінші курс студенттерінен құрылған таңдама репрезентативті
болмайды. Кездейсоқ таңдау процедурасын мысалға келесідей ұйымдастыруға
болады. Барлық студенттердің фамилияларын картоякаларға жазып аламыз, сосын
жақсылап араластырамыз да, барлық карточкалардың арасынан керек мөлшерін
таңдап аламыз. Осылайша таңдалған студнттердің жауаптары репрезентативті
таңдама құрайды. Егер таңдамада генеральды жиынтық құрайтын әртүрлі
топтардың элементтерін көрсету қажет болса, титі іріктеу процедурасы
қолданылады. Осылайша, егер бірінші курс студенттері университеттің барлық
студенттерінің 15% құрса, онда таңдамада да олар 15% құру керек. Кейбір
жағдайларда курсты ғана емес, сұрау нәтижелеріне әсер етсе сонымен қатар
студенттердің мамандығын да көрсету қажет.

КЕЗДЕЙСОҚ ШАМАНЫҢ ТАРАЛУ ЗАҢЫН ЗЕРТТЕУ

Қазіргі сандық медициналық-биологиялық эксперимент өзіндік жеке
математикалық зерттеу болып табылады. Ол экспериментті жоспарлаудан
басталады да, алынған нәтижелерді статистикалық өңдеумен аяқталады.
Медициналық-биологиялық эксперименттің көптеген сандық нәтижелері
кездейсоқ шамалар болып табылады. Кездейсоқ шама деп тәжірибе негізінде
алдын-ала белгісіз кез келген мәнге ие болатын шаманы айтады: X (x1, x2, x3
... .xi ... ..xn).
Кездейсоқ шаманың тарамдалу заңы деп кездейсоқ шаманың мүмкін мәндері
мен оларға сәйкес келетін ықтималдықтары арасында байланыс орнататын кез-
келген қатынасты айтады. Кезейсоқ шаманың тарамдалу заңы немесе тарамдалуы
осы шаманың мүмкін мәндерін анықтайтын толық сипаттама болып табылады және
түрлі мүмкін мәндердің ықтималдықтарын салыстыруға мүмкіндік береді.
Кезейсоқ шаманың тарамдалу заңы кесте, графика және формула (аналитикалық
түрде) түрінде беріле алады. Биологиялық белгілердің көптеген тарамдалулары
қалыпты заңға бағынады.
Графикалық түрде берілгенде абсцисс осімен кездейсоқ шаманың мәндері
алынады, ал ординаталар осімен кездесушіліктің абсолют жиілігі, таңдаманың
жалпы көлеміне қатысты проценті 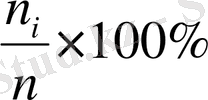, кездесушіліктің салыстырмалы жиілігі
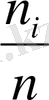(кездейсоқ шама мәндерінің ықтималдықтары) алынуы мүмкін.
Қалыпты таралудың қисығы центрге қатысты симметриялы, қоңырау тәрізді
түрі бар (1 сурет):

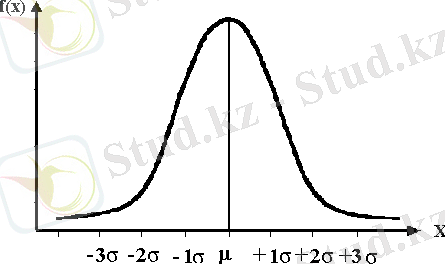
1 Сурет – Қалыпты таралудың қисығы
Таралу заңынан басқа кездейсоқ шамалар статистикалық сипатталармен
сипатталады.

МӘЛІМЕТТЕРДІ КЕСТЕЛЕР МЕН ГРАФИКТЕР ТҮРІНДЕ КӨРСЕТУ

Таңдама үлкен көлемде болғанда, оның элементтері топтарға
(разрядтарға) біріктіріледі, олар топталған статистикалық қатар түріндегі
тәжірибелер нәтижелері болып табылады. Ол үшін таңдаманың барлық
элементтерін қамтитын интервал k қиылыспайтын интервалдарға бөлінеді. Егер
интервалдардың ұзындықтары b=Rk (мұндағы R – кездейсоқ шаманың максимал
және минимал мәндерінің арасындағы айырма) бірдей болса, онда есептеулер
едәуір жеңілдейді. Топтама үшін интервалдар таңдалған соң, жиіліктер
анықталады — i-ші интервалға түскен таңдама элементтерінің ni саны
(интервалдың оң шекарасымен сәйкес келетін элемент келесі интервалға
жатады). Алынатын статистикалық қатардың жоғарғы жолында топтаманың
интервалдарының орталары бар, ал төменгі жолында — жиіліктер ni, (i= 1, 2,
..., k).
Жиіліктермен қатар жинақталған жиіліктер 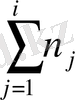, салыстырмалы жиіліктер
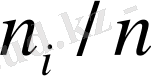және жинақталған салыстырмалы жиіліктер 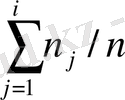, i=1,2 ... ., k
есептеледі. Алынған нәтижелер таңдама топтамасының жиіліктер кестесі деп
аталатын кестеге салынады.
Таңдаманы топтау келесі есептеулерге қателік әкеледі, ол интервалдар
саны азайған сайын өседі. Таңдама көлеміне байланысты интервалдар санын 6-
дан 15-ке дейін таңдайды.
Көрнекілік үшін таңдамалар жиіліктер гистограммасы және жиіліктер
полигонын қолданады.
Топталған таңдаманың жиіліктер гистограммасы деп топтама
интервалдарында тұрақты және олардың әрқайсысында сәйкес 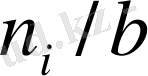, i=1,2 ... ., k
мәндерін қабылдайтын функцияны айтады.
Гистограмма графигінің үстіндегі фигураның ауданы n таңдама көлеміне
тең. Гистограмма мәндері жиіліктердің өздеріне проорционал болғандықтан,
әдетте ордината осі бойына 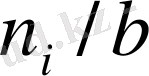мәндері емес, ni жиіліктердің мәндері
қойылады.
Осылайша салыстырмалы жиіліктер гистограммасы анықталады. Ол үшін
сәйкес фигураның ауданы бірге тең. Таңдама көлемі өскен сайын және топтама
интервалы азайған сайын, салыстырмалы жиіліктер гистограммасы генеральды
жиынтықтың f(x) тарамдалу тығыздығының статистикалық аналогы болып
табылады.
Жиіліктер полигоны деп ұштары 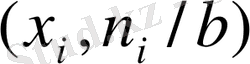, i=1,2 ... ., k нүктелеріндегі
сынықты айтады, ал салыстырмалы жиіліктер полигоны деп ұштары ,
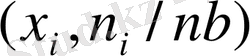i=1,2 ... ., k нүктелеріндегі сынықты айтады
Осылайша, салыстырмалы жиіліктер полигоны жиіліктер полигонын Оу осі
бойынша п рет сыққанда алынады. Гистограмма жағдайындағыдай, полигондарды
құру кезінде ордината осі бойынша жиіліктер немесе салыстырмалы жиіліктер
мәндері қойылады.
Огива (жинақталған жиіліктер көпбұрышы) деп топтаманың интервалдарының
оң шекараларымен сәйкес келетін абсциссалары, және сәйкес интервалдар үшін
жинақталған жиіліктер мәндерімен сәйкес келетін ординаталары бар ұштары бар
сынықты айтады. Егер сынық ұштарының ординаталары ретінде жинақталған
жиіліктердің процентпен алынған мәндері 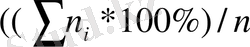қойылса, онда алынған график
проценттік огива деп аталады.
1 мысал. Таңдама берілген. Таңдаманы топтаманың жеті интервалын
қолданып, жиіліктер кестесі түрінде көрсету. Тарамдалу гистограммасы мен
огива құру.
18,3 15,4 17,2 19,2 23,3 18,1 21,9 15,3 16,8 13,2 20,4 16,5 19,7
20,5 14,3 20,1 16,8 14,7 20,8 19,5 15,3 19,3 17,8 16,2 15,7 22,8
21,9 12,5 10,1 21,1 18,3 14,7 14,5 18,5 18,4 13,9 19,1 18,5 20,2
23,8 16,7 20,4 19,5 17,2 19,6 17,8 21,3 17,5 19,4 17,8 13,5 17,8
11,8 18,6 19,1
Таңдама қарқыны R = 23,8-10,2=13,7. Топтама интервалының ұзындығы b =
13,77≈2.
Нәтижелері 1 кестеде және 2 суретте көрсетілген.
1 кесте
1 мысалды шешу нәтижелері
Интервал Интервал Интервал Жиілік Жинақталған Салыст. Жинақт.
нөмірі, шегі ортасы, , ni жиілік, Жиілік, салыст.
I жиілік,

1 10-12 11 2 2 0,0364 0,0364
2 12-14 13 4 6 0,0727 0,1091
3 14-16 15 8 14 0,1455 0,2546
4 16-18 17 12 26 0,2182 0,4728
5 18-20 19 16 42 0,2909 0,7637
6 20-22 21 10 52 0,1818 0,9455
7 22-24 23 3 55 0,0545 1,0000

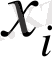
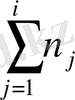
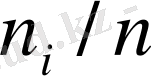
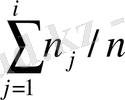
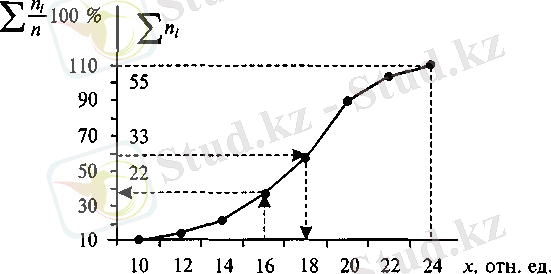
2 Сурет – 1 мысалдың мәліметтері үшін гистограмма және огива

КЕЗДЕЙСОҚ ШАМАЛАРДЫҢ НЕГІЗГІ СТАТИСТИКАЛЫҚ СИПАТТАМАЛАРЫ

Генеральды жиынтықты бірнеше сандық көрсеткіштермен сипаттау жиі
қажет болып тұрады. Таңдама бойынша осы таңдама сипаттамалар
(статистикалық сипаттамалар) деп аталатын сипатамалардың жуықталған
мәндерін (бағаларын) анықтауға болады.
1. Кездейсоқ шаманың орташа мәні (немесе М)

Қалып сипаттамасы болып табылады. Сандық осьтің қай жерінде
зерттелетін таңдама жатқанын көрсетеді. Бұл кездейсоқ шаманың барлық мүмкін
болатын мәндері топтасатын жуықталған шама.
2. Дисперсия – кездейсоқ шаманың шашырау сипаттамасы, оның орташа мәнге
қатысты шашырауы:

Дисперсия өлшемі х өлшенетін шаманың квадрат бірлігінде алынады.
3. Кездейсоқ шаманың қалыпты бірліктерде шашырауын анықтау үшін орташа
квадраттық ауытқу (стандартты ауытқу) шамасы қолданылады.:

4. Мода (Мо) – кездейсоқ шаманың ең жиі кездесетін мәні
11 12 12 13 13 13 14 14 15 16 16
5. Медиана (Ме) – таңдаманы қақ ортасынан бөлетін кездейсоқ шаманың мәні.
Барлық мәндерді ранжрленген қатарға орналастыру керек.
25 28 32 34 38 42 45 47 50
Таңдаманың 50% жоғары не төмен орналасқан мәнді көрсетеді.
6. Минимал мәні
7. Максимал мәні
8. Қадам
9. Орташа қатесі (стандартты) – таңдама көрсеткіштің (статистика) оның
генеральды параметрінен ауытқу шамасы:

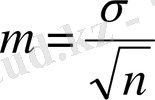
СЕНІМДІЛІК ИНТЕРВАЛЫ

Белгілі нүктелік таңдама сипаттамалар бойынша интервалды баға немесе
сенімділік интервалын құруға болады, онда қандай да бір ықтималдықпен
генеральды паратер орналасады. Белгілі таңдама көрсеткіштер негізіндегі
генеральды параметрлер туралы сенімді түрде айтуға келетін болып есептелген
ықтималдықтар сенімді деп аталады. Әдетте медициналық-биологиялық
зерттеулерде Р=0,95 (95%) сенімділік ықтималдығының мәні қолданылады. Және
де параметрдің нақты мәнінің осы шектерден шығу ықтималдығы 1–0,95=0,05
(5%)-тен аспайды. Сенімділік ықтималдықты толықтыратын шаманы әдетте α деп
белгілейді.
Орталық шекті теоремадан білетініміздей, таңдамалар алынған бастапқы
жиынтықтың тарамдалуына тәуелсіз таңдама орташалар жуықтап алғанда қалыпты
тарамдалуға ие. Осылайша, таңдама орташа мән үшін сенімділік интервалы
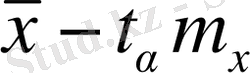және 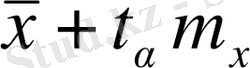мәндерінің арасында орналасқан, мұндағы mx орташаның
стандартты қатесі, tα – Стьюдент коэффициенті, п таңдама көлеміне тәуелді
(немесе сәйкес f бостандық дәрежелірінің саны) шама және сенімділік
ықтималдығының таңдалған деңгейіне тәуелді шама Стьюдент тарамдалу
кестелері бойынша анықталады. tα коэффициент шамасы сенімділік
ықтималдығын 1-ге дейін толықтыратын α деңгейінде кесте бойынша анықталады,
яғни сенімділік ықтималдығы 95% жағдайда интервал симметриясы ескерілгенде
(1-0,95)=0,05 деңгейінде.

СТАТИСТИКАЛЫҚ БОЛЖАМДАР ЖӘНЕ ОЛАРДЫ ТЕКСЕРУ

Салыстырылатын топтардың артықшылықтарын олардың бөлшектері, орташа
бөлшектері немесе басқа көрсыткіштері аласындағы айырмашылықтары арқылы
көреді. Бұл қортынды көрсеткіштің статистикалық және кездеисоқ бағасы болып
келеді. Айырмашылықтардың айқындылығы белгілі статистикалық болжамдарды
тексеру арқылы анықталады.
Клиникалық зертеулерде нолдік болжам Но кеңінен қолданылады. Бұл
болжам салыстырылатын топтардың шешуші көрсеткіштері нолге тең және олардың
арасындағы айырмашылық кездейсоқ сипатқа ие болуына негізделген. Мысалы,
егер бір таңдама 1 және σ1 көрсеткіштерімен ал екіншісі 2 және
σ2 қ корсеткіштерімен қалыпты таратылған жиынтықтан алынса, онда нолдік
болжам 1 = 2, яғни. 1- 2 = 0 болады.
Нолдік болжамға қарама-қарсы – алтернативті болжам. Бұл болжам орташа
көрсеткіштері дұрыс емес 2 - l ≠ 0 (екі жақты тест) немесе
зерттеуші бір әдістің басқа әдістен артықшылығына негізделген, мысалы
1 2 (бір жақты тест). Бұл кезде бар айырмашылықтардың көлемдік
көрсеткіштерін бағалау қажет етпейді, текқана зерттелетін екі топтың түрлі
жиынтықтарға жататынына сену керек. Осындай жағдайда бар айырмаларды сандық
бағалау мақсаты қойылмайды, екі топ та нақты ықтималдықпен түрлі генеральды
жиынтықтарға қатысын тексеру жеткілікті. Басқа статистикалық есептерді шешу
кезінде нольдік болжам басқа түрге ие болады.
Статстикалық болжам тарамдалу функциялары белгілі және табулирленген
шамалардың немесе, басқа сөзбен айтқанда, статистикалардың көмегімен
тексеріледі (мысалы, Стьюденттің t-тарамдалуы, χ2 тарамдалу және т.б.). Бұл
шамалар әрбір нақты жағдайда таңдама көрсеткіштердің айтылған болжамды
қанағаттыратынын анықтауға мүмкіндік береді. Болжамды тексеру процедурасы
таңдама көлеміне (немесе сәйкес f бостандық дәрежелерінің санына) және α
мәнділік деңгейімен байланысты. Мәнділік деңгейі немесе қабылданған
болжамды бағалау кезінде мүмкін болатын І типті қате ықтималдығы басқа
болуы мүмкін (5, 1, 0,1%), бірақ медициналық-биологиялық қосымшаларда егер
арнайы басқа мән қарастырылмаса, ол әдетте 5%-ке тең де алынады. Егер
нәтижелер 1-5% деңгейде мәнді болса, онда әдетте статистикалық болжам бары
туралы айтады, 1% -тен кем деңгейде – жоғары статистикалық мәнділік туралы
айтады.
Мәнділік деңгейімен нольдік болжамға сенімсіздік дәрежесі деп аталатын
шама байланысты. Ол мәнділік деңгейді бірге дейін толықтыратын (1 - α) шама
болып табылады. Нольге жақын мәнділік деңгейі, яғни бірге жақын сенімсіздік
дәрежесі нольдік болжамға қарсы күшті аргумент ретінде қабылданады. Бірге
жақын мәнділік деңгейі сенімсіздік дәрежесінің нольге жақындығын көрсетеді,
яғни Н0 –ге қарсы аргументтер әлсіз, бұл бар мәліметтердің нольдік
болжаммен келісімді екенін көрсетеді.
Нольдік болжамның растығы туралы сұрақ та маңызды болы табылады. Н0
растылықты бағалау үшін р-мән есептеледі. Ол нольдік болжамның рас кезінде,
яғни салыстырылатын топтар арасындай өзгешелік болмағанда, зерттеуді
бірнеше рет қайталап, тура сондай мән немесе одан гөрі экстремалды мән алу
ықтималдығын бағалайды деп айтуға болады. Егер нольдік болжамды тексеру
барысында ол α мәнділік деңгейінде қабылданбаған болса, онда статистикалық
мәнді өзгешеліктер барын көрсету үшін салыстыру нәтижесі р α түрінде
жазылуы мүмкін. Бұл нольдік болжас дұрыс болғанда салыстыру қатесі α•100%-
тен көп емес жағдайда мүмкін, яғни қате болу ықтималдығы аз дегенді
білдіреді.
Бірақ жиі қолданылатын р 0,05 жазуы нәтижелердің мәнділік деңгейі 5%-
тен кем еместігін білдіреді. Мәнділік деңгейі туралы ақпарат, мысалы 0,01
р 0,05 екілік теңсіздік жазуында көбірек болады.
р-мән тек теңсіздікпен ғана беріліп қоймайды. Оның мәнін нақты
есептеуге болады және бұл процедура болжамды тексерудің қарапайым
процедурасына кері болып табылады. Ол үшін тестілік статистика шамасы
есептеледі, сосын, мысалы, осы критерийге қатысты кестелер бойынша (немесе
критерий статистикасының мәнін оның тарамдалу функциясына келтіру
нәтижесінде) тестілік статистиканың бағаланған мәніне сәйкес келетін
ықтималдық деңгейі анықталады. Осындай процедура кезінде, Н0 болжамын
қабылдау (қабылдамау) шешіміне келгенде, біз нольдік болжамды қабылдау
(қабылдамау) жүзеге асатын р-мәнге тең деңгейдің нақты мәнін көрсетеміз.
Нақты р-мәнді көрсету болжамды рα теңсіздік түрінде тексеру нәтижелерін
сипаттаудан гөрі ақпаратты болып табылады..
Клиникалық зерттеулер саласында айырмалардың статистикалық мәнділігі
туралы болжам тексеріледі, бірақ статистикада басқа да варианттар барын
ескеру керек, мысалы тарамдалу келісімдігі (немесе формасы) туралы болжам,
корреляция мәнділігі туралы болжам, тарамдалу параметрлерінің шамасы туралы
болжам және т.б. Болжамның нақты формулировкасына қарамастан статистикалық
болжамдарды тексеру процедурасының типтік кезеңдерінің қысқаша сипаттамасын
беруге болады. Келесі әрекеттер барлық статистикалық тексерулердің
негізінде жатыр:
• α мәнділік деңгейін таңдау;
• нольдік болжам құрастыру Н0 (әдетте қабылдамай қойғымыз келетін
қорытынды ретінде) және міндетті түрде оған сәйкес келетін
альтернативті болжам Н1;
• тестілік статистика таңдау немесе, басқа сөзбен, құрастырылған болжамды
тексеру үшін келетін критерий;
• бар мәліметтер бойынша тестілік статистика мәнін есептеу;
• тестілік статистика тарамдалуының көмегімен немесе әдетте оның
тарамдалуының кестелері бойынша нольдік болжам дұрыс болған жағдайда
кіру ықтималдығы α болатын критикалық облысты анықтау;
• статистиканың есептелген мәнін таңдалған критикалық мәнмен салыстырып,
қорытынды жасау.
Биометрияда болжамдарды тексеру үшін критерийдің екі түрі мүмкін:
параметрлік (осы жиынтықтың параметрлерінің негізінде құрылған) және
параметрлік емес (осы жиынтықтың варианттары және жиіліктері бойынша
құрылған).

ОРТАША МӘНДЕР АРАСЫНДА АЙЫРМАШЫЛЫҚ БАР (НЕМЕСЕ ЖОҚ) ТУРАЛЫ БОЛЖАМДЫ ТЕКСЕРУ
ҮШІН ПАРАМЕТРЛІК КРИТЕРИЙЛЕР

Параметрлік критерийлер қалыпты заңмен тарамдаған кездейсоқ шамалар
үшін қолданылады, параметрлік емес критерийлер сапалы белгілер үшін,
белгісіз тарамдалу кезінде, кішкентай таңдамалар үшін қолданылады.
Сонымен, егер сіздің таңдамаларыңыз қалыпты тарамдалған болса, онда
олардың негізінде статистикалық болжамдарды тексеру үшін параметрлік
критерийлерді қолдануға болады. Салыстырылатын екі орташа мән арасындағы
айырмаларды бағалаудың ең таралған параметрлік әдісі Стьюдент критерийі
немесе t-критерий болып табылады.
Мұнда екі жағдай болу мүмкін: таңдамалар тәуелсіз және тәуелді болса.
Таңдамалар тәуелсіз болған жағдайда, екі орташаның теңдігі туралы
нольдік болжамды тексереміз (яғни екі таңдама бір генеральды жиынтықтан
алынған).
Тексерілетін t-критерий сәйкес таңдама орташалардың айырмасының
осындай айырманың қатесіне қатынасы түрінде өрнектеледі, яғни

Мұнда mx1, mx2 — салыстырылған таңдамалардың орташа мәндерінің
стандарттық қателері. Бұл жерде көңіл аударатыны мынау, екі орташа мәннің
айырмасының дисперсиясы (сумма дисперсиясы сияқты) осы орташа мәндердің
дисперсияларының суммасына тең.
Критерийді тексеру үшін орташа мәндердің теріс таңбасы ешқандай роль
атқармайды, сондықтан тестілік статистиканы есептеу формуласында айырманың
модулі алынады. Бірақ айырма таңбасы салыстыру нәтижелерін интерпретациялау
және салыстыру әдістерінің біреуінің артықшылығы туралы қорытынды жасау
үшін маңызды.
Егер t-критерийдің алынған нақты мәні алынған мәнділік деңгейі және f
() бостандық дәрежелері саны үшін Стьюдент тарамдалуының кестелік
мәнінен асып түссе немесе тең болса, математикалық күту теңдігі болжамы
қаралмайды. Яғни: .
Және де сәйкес мәнділік деңгейінде орташа мәндер арасында
статистикалық мәнде айырмалар бары туралы қорытынды жасалады.
2 мысал. Сау адамдар және гепатитпен ауыратындар тобында қан іркітінде
ақуыз құрамы анықталды. Сау адамдар және гепатитпен ауыратындар тобында
ақуыз құрамындағы айырмашылық барын анықтау, α=0,05.
X1 (қалып) 6,87 6,51 6,9 7,05 7
X2 (гепатит) 7,2 6,92 7,52 7,18 7,25 7,1

Н(0) – сау адамдар және гепатитпен ауыратындар тобында ақуыз
құрамындағы айырмашылық жоқ.
Екі таңдамалар орташа мәндерін есептейміз:

Таңдамалардың орташа квадраттық ауытқулары:
және
Стандарттық қателерді табамыз:
және
t-критерийді есептейміз:

Р=0,95 және (n1-1)+( n2-1)=10 бостандық дәрежелерінің саны үшін
tкрит=2,26 деп анықтадық.
tесеп tкрит (2,652,26), яғни нольдік болжам қабылданбайды.
Қорытынды: Қалыптағы алынған ақуыз құрамы α=0,05 кезінде гепатит
ауруында қанда ақуыз құрамынан статистикалық айырмашылығы бар.

Екі тәуелді таңдаманы немесе жұптаса байланысқан варианттары бар
таңдамаларды салыстыру үшін олардың жұп айырмаларының орташа мәнінің нольге
теңдік болжамы тексеріледі. Бұндай жағдай әрбір пациенттің бізді
қызықтыратын белгісінде өзгерістер туралы мәліметтер болғанда туындайды.
Мысалы, егер пациенттер тобы зерттелетін емдеу тәсілін қолданса және әрбір
пациентте емдеуге дейін және емдеуден кейін белгінің мәні өлшеніп отырса.
Бұл жағдайда терапияны алу нәтижесінде осы белгінің өзгерістерінің нольге
теңдігі туралы нольдік болжамы тексерілу керек. Бұл жағдайда генеральды
орташалар арасындағы айырмаларды бағалау ретінде жұп айырмалар суммасынан
анықталатын орташа айырма алынады. Орташалар айырмасының генеральды
дисперсиясын бағалау болып таңдама дисперсия алынады
Егер генеральды жиынтық мүшелері қалыпты тарамдалса, онда олардың
арасындағы айырмалар да қалыпты тарамдалады. Сондықтан көрсеткіш мәндерінің
өзгерісінің нольге теңдігі туралы нольдік болжамды тексеру үшін тестілік
қатынас есептеледі:

мұндағы - орташа айырма ( — байланысқан варианттардың жұп
айырмалары, п – жұп бақылаулардың саны).
Алынған мәнділік деңгейі және f=п-1 бостандық дәрежелері саны үшін
Стьюдент тарамалуының кестелері бойынша тексеріледі, екі жақты тест
жағдайында таңба қарастырылмайды. Есептелген мән сәйкес кестелік мәннен
асып түссе, осы мәнділік деңгейі үшін нольдік болжам қабылданбайды.
3 мысал. Гипертониямен ауыратын 6 аурудан тұратын топта артериялық
қысымын азайтатын адельфан дәрмегінің әсері зерттелді. Тәжірибе нәтижесінде
систолиялық қысымның 2 вариациялық қатары алынды: біріншісі – дәрмекті
қабылдағанға дейін (бақылау), екіншісі – дәрмекті қабылдағаннан кейін
(тәжірибе):
Бақылау 250 240 210 190 185 170
Тәжірибе 210 195 165 170 155 175

Адельфанды қабылдағаннан кейін систолиялық артериялық қысым қандай
шамаға азаяды? Алынған нәтижелер нақты ма?
Біріншіден, жұп айырмаларды есептеп шығамыз:
xki (бақылау) хoi (тәжірибе) di (қысымдар айырмасы)
250 210 -40
240 195 -45
210 165 -45
190 170 -20
185 155 -30
170 175 5

Айырмалар қатары үшін статистикалық параметрлерді есептейміз:

tесеп анықтаймыз:

Стьюдент кестесі бойынша Р=0,95 және n-1=5 бостандық дәрежелері саны
үшін tкрит=2,57.
tесеп tкрит – яғни нольдік болжам қабылданбайды.
Қорытынды: Адельфан дәрмегін қабылдау Р0,95 ықтималдықпен артериялық
қысымын 29,17207,5*100%=14%-ке төмендетеді.
t-критерийді дұрыс қолдану үшін салыстырылатын таңдамалар алынып
тасталған жиынтықтардың қалыпты тарамдалуы болу керек. Егер бұл шарт
орындалмаса, онда параметрлік емес критерийлер тиімді болады.

ОРТАША МӘНДЕ АРАСЫНДА АЙЫРМАШЫЛЫҚ БАР (НЕМЕСЕ ЖОҚ) ТУРАЛЫ БОЛЖАМДЫ ТЕКСЕРУ
ҮШІН ПАРАМЕТРЛІК ЕМЕС КРИТЕРИЙЛЕР

Орташа мәндерді салыстыру үшін параметрлік емес критерийлердің толық
қатары қолданыла алады, олардың ішінде маңызды орынды рангілі критерийлер
алады. Осы критерийлерді қолдану салыстырылатын топтардың мүшелерін
ранжирлеуге негізделген. Бұнда ранжирленген қатардың мүшелері
салыстырылмайды, олардың реттік нөмірдері немесе рангілері салыстырылады.
Салыстырылатын тәуелсіз таңдамалардың бір генеральды жиынтыққа қатысы
туралы болжамды тексеру үшін Манна—Уитни U-критерийін келтіреміз.
Екі таңдаманың барлық мәндерін бір қатарға өсу ретімен біріктіреміз.
Осы қатардың әрбір элементіне 1-ден N= n1 + n2 –ға дейін номер (ранг)
береміз. Егер қатардың бірнеше элементтері шамалары бойынша сәйкес келсе,
онда әрқайсысына олардың номерлерінің арифметикалық орташасына тең ранг
беріледі. Бірінші таңдаманың R1 рангілерінің суммасын және екінші
таңдаманың R2 рангілерінің суммасын анықтаймыз және статистикаларды
есептейміз:

U критерийі ретінде осы сандардың ең кішісін таңдаймыз. Егер оның мәні
кестеде α мәнділік деңгейінің бойында және f бостандық дәрежелерінің саны
(кіші таңдама көлемі) үшін көрсетілген критикалық мәннен үлкен болса, онда
нольдік болжам қабылданады, яғни таңдамалар арасындағы айырмашылықтар
сенімді емес. Кері жағдайда Н(1) қабылданады.
Егер гольдік болжам дұрыс болса және таңдамалар бір генеральды
жиынтықтан алынса, онда біріккен вариациялық қатардың бір жағынан бір
таңдаманың бақылаулары артық болады дей алмаймыз. Олардың мәндері барлық
жалпыланған қатар бойымен біртекті тарамдалған болу керек. Осылайша, R
статистиканың өте үлкен немесе өте кішкентай мәндері гольдік болжамның
дұрыстығына күмән келтіреді.
4 мысал. Манна-Уитни критерийі көмегімен тәуелсіз таңдамалар бір
генеральдық жиынтықтан шыққан туралы болжамды тексерейік (2 кесте).
2 Кесте
Дәрмек затының қандағы мөлшері, ммольг
1 топ 8 8 9 10 7 7 9 9 11

Жұп айырмашылықтарды бір қатарға ранжирлейміз. Таңбасына қарамастан
келесі қатарды аламыз:
-0,1 0,2 -0,4 0,7 0,8 -0,9 -1,0 1,1 1,3 1,5
1 2 3 4 5 6 7 8 9 10

Жеке түрде оң (Т+) және теріс (Т-) айырмашылықтардың рангілерінің
суммасын есептейміз:
(Т+) = 2+4+5+8+9+10=38, (Т-) = 1+3+6+7=17
Екі жақты Т-критерийін тексеру үшін кіші статистиканы алып Т-=17, оны
n=10 жұп айырмашылықтар саны үшін және мәнділік деңгейі 5% үшін кестелік
мәнмен салыстырамыз. Ондай кестелік критикалық мән 9-ға тең. Есептелген Т-
статистиканың минималды мәні сәйкес кестелік мәнінен асып түсті, яғни
нольдік болжам күшінде қалады.

БЕЛГІЛЕРДІҢ ҚИЫСУ КЕСТЕСІ

Өлшеуге қиын немесе мүлдем мүмкіндік туғызбайтын белгілер, түрлі
құбылыстар және заттар өте көп. Мысалы, мамандық немесе патология түрі
белгілерін қалай өлшеуге болады, осы белгілерді профессионалды ауру туралы
статистикалық көрініс алу үшін қалай салыстыруға болады?
Алдымен, зерттелетін белгілер арасында қандай да бір байланыс барын
анықтау керек, әлде олар бір-біріне тәуелсіз әрекет ете ме.
6 мысал: Екі тәуелсіз пациенттер топтары бар: ауыл тұрғындары және
қала тұрғындары. Осы топтарда анемиямен ауыратын пациенттер үлесі бірдей
ме, яғни анемияның таралуы тұрғылықты орынға тәуелді ме деген сұраққа жауап
табу керек. Нольдік болжамды – анемияның таралуы тұрғылықты орынға тәуелді
емес деп аламыз.
Анемия бар тобында а адамар қала тұрғындары болып келеді, b – ауыл
тұрғындары. Анемия жоқ тобында с адамар қала тұрғындары болып келеді, d –
ауыл тұрғындары (3 кесте).
3 кесте
Анемия таралуының зерттеу нәтижелері
Қасиет Қалалық Ауылдық Барлығы
Анемия бар a b a+b
Анемия жоқ c d с+d
Барлығы n2=b+ d

Бұл жағдайда (хи-квадрат) критерийді қолдануға болады:

Берілген мәнділік деңгейі α және бостандық деңгейлерінің саны f=1 үшін
оның критикалық мәнін анықтаймыз. Егер , онда нольдік болжам
қабылданады, яғни анемияның таралуы тұрғылықты орнына тәуелді емес деп α
ықтмалдықпен айтуға болады.
Егер , онда альтернативті болжам қабылданады.
7 мысал. Қандай да бір дәрмек температураны төмендететіні зерттелді
(тәуелді топтар). Дәрі қабылдауының алдында жоғары температурасы бар
адамдар тобында дәріні қабылдағаннан кейін a адамдардың жоғары
температурасы сақталынды, ал b адамдардың температурасы қалпына келді. Дәрі
қабылдауының алдында жоғары температурасы жоқ адамдар тобында дәріні
қабылдағаннан кейін с адамдардың температурасы көтерілді, ал d адамдардың
температурасы өз қалпында қалды (4 кесте).
4 кесте
Дәрмектің температураға әсері
Кейін температура барКейін температура жоқ
Дейін температураa b
бар
Дейін температураc d
жоқ

Нольдік болжамды – дәрмек температураға әсер етпейді, яғни
температурасы бар және жоқ адамдардың қатынасы дәрмек қабылдаған соң
өзгерген жоқ деп аламыз.
критерий бойынша есептейміз:

Егер онда нольдік болжам қабылданады, яғни дәрмек температураға
әсер етпейді деп α ықтималдықпен айтуға болады.
Егер онда альтернативті болжам қабылданады, яғни дәрмек
температураны азайтады.

БІРФАКТОРЛЫ ДИСПЕРСИЯЛЫҚ ТАЛДАУ

Кездейсоқ шамалардың өзгеруі (вариациясы) бірқатар себептердің
(факторлардың) әрекетінен туындайды. Мысалы, дененің әртүрлі параметрлері
(температура, артериалды қысым) тәулік уақытына байланысты өзгереді, қандай
да бір фармакологиялық дәрмек қабылдағанда өзгереді, т.с.с. Зерттелетін
белгіле қандай да факторлардың әсерін таза түрде бөліп шығару мүмкін емес.
Тәжірибе кезінде жағдайларды максималды түрде біртекті етіп сақтауға
тырысқанмен, түрлі тәжірибелер әртүрлі нәтижелер береді. Бұл осы
факторларға көптеген кездейсоқ жағдайлар, көптеген бақылауға алынбайтын
фаткорлар әсер ететінімен түсіндіреледі. Сондықтан белгінің жалпы
өзгергіштігін құрамды бөліктерге бөлу қажеттілігі туындайды, бір жағынан
нақты факторлармен анықталады, екінші жағынан бақылауға алынбайтын
кездейсоқ себептермен туындайды.
Факторлардың кездейсоқ шама өзгергіштігіне әсерін зерттейтін
статистика бөлімін дисперсиялық талдау деп атайды. Дисперсиялық талдау
мақсаты – кездейсоқ шаманың өзгеруіне әсер ететін факторлар мен олардың
тіркесімін бөліп алу. Ескерілетін факторлар санына байланысты бірфакторлы
және көпфакторлы дисперсиялық талдау болып бөлінеді.
8 мысал. Тамақтану рациондарының жануарлардың салмағының артуын әсері
зерттеледі.
Фактор – ұл тамақтану рационы, оның деңгейлері
• Тек макарондар
• Тек ет
• Тек жемістер
• Қалыпты рацион (бақылау тобы)
Бұл жағдайда зерттеу жаунарлардың 4 тобына жүргізілді. Бірінші
тәжірибенің нәтижелері суретте көрсетіген (3 сурет).

3 Сурет – 1-ші тәжірибедегі тамақтану рациондары бойынша жануарлар
топтарының салмақтарының көрсеткіштері
Суретте көрсетілгендей, топтар ішінде салмақ көрсеткішінің шашырауы
топтар бойынша орташа мәндердің шашырауына қарағанда көбірек.
Яғни келесі болжам жасауға болады: осы топтардағы жануарлар салмағы
тамақтану рационына қатты тәуелді емес, ал топтар ішіндегі шашырауды осы
зерттеудегі қарастырылмаған фокторлармен түсіндіруге болады.
Екінші тәжірибеде басқа мәліметтер алынды (4 сурет):

4 Сурет – 2-ші тәжірибедегі тамақтану рациондары бойынша жануарлар
топтарының салмақтарының көрсеткіштері
Бұл жағдайда орташа мәндердің шашырауы ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.