Интегралдық есептеудің геометриялық және физикалық есептерге қолданылуы

Кіріспе ... ... ... ... ... . 3
1. Интегралдық есептердің гео.
метриялық есептерге қолдануы ... .. 4
1.1. Ауданның анықтамасы ... .. 4
1.2. Жазық фигуралардың ауданын
интеграл арқылы өрнектеу ... ... ... 6
1.3. Доғаның ұзындығы ... ... ... ... 11
1.4. Денелердің көлемін анықталған
интеграл арқылы өрнектеу ... ... ... 14
2. Анықталған интегралдың физикалық
қолдануы ... ... ... ... ... ... .. 22
2.1. Анықталған интегралдың физикалық
есептерге қолданылуы ... ... ... ... 22
2.2. Гульдиннің I теоремасы ... .. 23
2.3. Гульдиннің II теоремасы ... 24
3. Практикалық бөлім ... ... ... ... ... ... ... 31
Қорытынды ... ... ... ... ... ... ... ... ... ... . 33
Қолданылған әдебиеттер

Анықталған интеграл арқылы жазық фигуралардың ауданы, қисық сызықтардың ұзындығы, дененің көлемі мен беті, ауырлық центрінің координаттары, инерция моменттері, берілген күштің атқаратын жұмысы, т.б. жаратылыстану мен техника есептері шешіледі. Интеграл ұғымы көп айнымалысы бар функцияларға да қолданылады. Интегралдық есептеудің аудан мен көлемді табуға байланысты бірқатар есептерін ежелгі грек математиктері шешкен. 9 – 15-ғасырларда Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Бірақ оларды одан әрі дамыта алмады. Тек 16 – 17-ғасырларда ғана табиғаттану ғылымдарының жетістіктері интегралдық есептеудің одан әрі дамуын қажет етті. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. «Интегралдық есептеу» термині мен интеграл таңбасы Лейбництен бастап қолданылып келеді. Интегралдық есептеудің әрі қарай дамуы швейцариялық математик Иоганн Бернуллидің, әсіресе, Леонард Эйлердің есімдерімен тығыз байланысты. 19-ғасырдың басында француз математигі Огюстен Луи Коши шектер теориясы негізінде интегралдық есептеу мен дифференциалдық есептеуді қайта құрды. Интегралдық есептеуді дамытуға 19-ғасырда орыс ғалымдары Михаил Остроградский, Виктор Буняковский және Пафнутий Чебышев үлкен үлес қосты. 19-ғасырдың аяғында және 20-ғасырдың басында жиын теориясының дамуы интегралдық есептеудің негізгі ұғымдарының тереңдеуіне және кеңеюіне себеп болды.

1. О.А.Жәутіков. «Математикалық анализ курсы» , Алматы, «Экономика» баспасы, 2014 жыл.
2. Темірғалиев Н.Т. Математикалық анализ 1,2,3-том. Алматы 1977 ж
3. Әубәкір С.Б. Жоғары математика. 1-2 бөлім. – Алматы, ҚАЗҰУ, 2000 ж.
4. Қасымов Қ., Қасымов Е. Жоғары математика курсы. –Алматы, Санат, 1994ж.
5. Қабдықайыров Қ. Жоғары математика.-Алматы, РБК, 1993.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 36 бет
Таңдаулыға:

Қостанай мемлекеттік педагогикалық институты
Жаратылыстану-математика факультеті
Физика-математика және жалпы техникалық пәндер кафедрасы

Базарбай Ақсұлтан Ерболұлы

Интегралдық есептеудің геометриялық және физикалық есептерге қолданылуы

Курстық жұмыс

Ғылыми жетекші:Доспулова У.К.
аға оқытушы

Қостанай, 2015ж.
Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 3
1. Интегралдық есептердің гео-
метриялық есептерге қолдануы ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 4
1.1. Ауданның анықтамасы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 4
1.2. Жазық фигуралардың ауданын
интеграл арқылы өрнектеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 6
1.3. Доғаның ұзындығы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 11
1.4. Денелердің көлемін анықталған
интеграл арқылы өрнектеу ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 14
2. Анықталған интегралдың физикалық
қолдануы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 22
2.1. Анықталған интегралдың физикалық
есептерге қолданылуы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 22
2.2. Гульдиннің I теоремасы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 23
2.3. Гульдиннің II теоремасы ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 24
3. Практикалық бөлім ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .. 31
Қорытынды ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 33
Қолданылған әдебиеттер ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 34

Кіріспе

Анықталған интеграл арқылы жазық фигуралардың ауданы, қисық сызықтардың ұзындығы, дененің көлемі мен беті, ауырлық центрінің координаттары, инерция моменттері, берілген күштің атқаратын жұмысы, т.б. жаратылыстану мен техника есептері шешіледі. Интеграл ұғымы көп айнымалысы бар функцияларға да қолданылады. Интегралдық есептеудің аудан мен көлемді табуға байланысты бірқатар есептерін ежелгі грек математиктері шешкен. 9 - 15-ғасырларда Орта және Таяу Шығыс ғалымдары Архимед еңбектерін араб тіліне аударып, ежелгі математиканың табыстарын кейінгі ұрпақтарға жеткізді. Бірақ оларды одан әрі дамыта алмады. Тек 16 - 17-ғасырларда ғана табиғаттану ғылымдарының жетістіктері интегралдық есептеудің одан әрі дамуын қажет етті. Интегралдық есептеудің негізгі ұғымдары мен идеялық жүйесін бір-біріне тәуелсіз түрде Исаак Ньютон мен Готфрид Лейбниц жасады. Интегралдық есептеу термині мен интеграл таңбасы Лейбництен бастап қолданылып келеді. Интегралдық есептеудің әрі қарай дамуы швейцариялық математик Иоганн Бернуллидің, әсіресе, Леонард Эйлердің есімдерімен тығыз байланысты. 19-ғасырдың басында француз математигі Огюстен Луи Коши шектер теориясы негізінде интегралдық есептеу мен дифференциалдық есептеуді қайта құрды. Интегралдық есептеуді дамытуға 19-ғасырда орыс ғалымдары Михаил Остроградский, Виктор Буняковский және Пафнутий Чебышев үлкен үлес қосты. 19-ғасырдың аяғында және 20-ғасырдың басында жиын теориясының дамуы интегралдық есептеудің негізгі ұғымдарының тереңдеуіне және кеңеюіне себеп болды.
Зерттеудің өзектілігі: курстық жұмыстың мазмұнының ғылыми құндылығын арттыру және оның негізінде пәнге деген қызығушылығын арттырып, өз бетінше іздену. Білім, білік, дағды алуын қамтамасыз етуге, жеке шығармашылық қабілеті дамуы үшін жағдай туғызу.
Мақсаты: Интегралдық есептердің геометриялық есептерге қолданылуын зерттеу.
Міндеті: - Анықталған интегралдың геометриялық есептерге қолдануы.
- Анықталған интегралдың физикалық қолдануы.
- Анықталған интегралдың геометриялық және физикалық есептерді қолданылуына есептер мен мысалдар қарастыру.
Зерттеу обьектісі: Математикалық талдау.
Зерттеу пәні: Интегралдық есептеудің геометриялық және физикалық есептерге
Зерттеу әдістері: Талдау нәтижесінде алынған мәліметтерді бақылап, тақырып бойынша әдебиеттерді зерттеу.
Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, практикалық жұмыс, қорытынды және қолданылған әдебиеттер тізімінен тұрады.

Интегралдық есептердің геометриялық есептерге қолдануы

1.1. Ауданның анықтамасы

Көпбұрышты облыс немесе тек қана көпбұрыш деп бір немесе бірнеше тұйық сынық сызықтармен қоршалған жазық фигураны айтамыз. Мұндай фигура үшін аудан ұғымы мектепте оқылған геометрия курсынан әрқайсымызға белгілі. Сондықтан осы ұғымды негізге аламыз.
Жазықтықта жатқан бір үздіксіз тұйық сызықты қарайық. Бұл тұйық сызықты (С) деп белгілейік.
Осы айтылған бейнелі тұйық қисық бүкіл жазықтықты екі - ішкі және сыртқы -- облысқа бөлетінін француздың атақты математигі К. Жордан көрсетті.
Қисық сызық (С)-ні облыстың жиегі немесе контуры деп атайды.
Тұйық (С) қисық сызықпен қоршалған облысты, яғни фигураны D арқылы белгілейік.
D облысының ішінде жатқан түрлі-түрлі көпбұрыштарды қарайық, бұл көпбұрыштардың жиынын { арқылы, ал олардың аудандарының шамаларын р деп белгілейік. Мұнымен бірге D облысын өздерінің ішінде тұтып тұратын түрлі-түрлі көпбұрыштар жиынын {В} арқылы, ал олардың аудандарының шамаларын Р деп белгілейік. Сонда, көпбұрыштар қандай болса да, әрқашан р Р, бұл теңсіздіктен біз мынадай қорытындыға келеміз: егер р сандарынан тұратын жиынды {р}, ал Р сандарынан тұратын жиынды {Р} деп белгілесек, онда жиын {р} жоғары жағынан {Р} жиынның кез келген элементімен шектелген. Сондықтан {р} жиынынығы дәл жоғарғы шекаралығы болады, оны u деп белгілейік. Сонда u = Р.
Жиын {Р} төменгі жағынан {р} жиынының кез келген элементімен шектелген, сондықтан {Р} жиынының дәл төменгі шекаралығы болады. Оны v деп белгілейік. Мұнда v = р. Ал u мен v-нің арасындағы қатыс былай болуы керек: u=v. u санын D облысының ішкі. v санын оның сыртқы ауданы деп атауға болады.
Егер осы екі дәл шекаралық v = sup{р} мен v = inf{Р} бір-бірімен тең болса, онда D облысын квадратталынатын фигура деп атайды, ал u = v = Q санын осы фигураның ауданы үшін алады.
Облыс D квадратталынатын фигура болу үшін кез келген оң ε санына сәйкес, облыс D -ні өздерінің ішінде тұтып тұратын көпбұрыш В және облыстың ішінде жататын көпбұрыш А табылып, осы көпбұрыштардың аудандарының айырмасы Р-р берілген ε санынан кіші болуы қажетті және жеткілікті.
Егер облыс D - квадратталынатын фигура болса, онда р u - t2, ал Р u + t2, бұл арадан Р - р ε. Сонымен, біз қажеттілігін дәлелдедік.
Жеткіліктілігін мына теңсіздіктерден
р =u=v= Р
шығаруға болады.
(С) - облыс D - нің контуры болсын. Егер облыс D квадратталынатын болса, онда контур (С), (В -- А) көпбұрыштың ішінде жатады, ал бұл көпбұрыштың ауданы мына теңсіздікті Р - р ε қанагаттандырады, өйткені көпбұрыш (В - А), А мен В көпбұрыштарының контурларының арасында жатады.
Контур (С), ауданы кез келген оң құнарсыз аз ε санынан кіші көпбұрыш (L) -нің ішінде жатады деп ұйғарайық. Егер (L)-дің ауданы R деп белгілесек, онда R ε . Ал екінші жағынан
Р - р = R ε.
Егер берілген (К) қисығын қоршап тұрған көп бұрыштың ауданы мейлінше (құнарсыз) аз болса, онда (К) сызығының ауданы ноль болады дейміз. Осы анықтамадан кейін, облыстың квадратталыну шартын екінші түрде былай тұжырымдауға болады.
Облыс D квадратталынатын фигура болу үшін оның контуры (С)-нің ауданы ноль болуы қажетті және жеткілікті шарт.
Ашық у = f(х), а = х = b немесе х = φ(у), с = у = d теңдеумен берілген әрбір үздіксіз қисықтың ауданы ноль болады.
ε 0 алдын ала берілген оң құнарсыз аз сан болсын. Онда осы ε бойынша δ 0 санын тауып алып, [а,b] аралығын, әрбір бөлшек сегменттің ұзындығы δ санынан кіші болатындай етіп n бөлшек сегменттерге бөлеміз. Функция f (х) = у, [а, b] аралығында үздіксіз болғандықтан, оның әрбір бөлшек сегменттегі тербелісі ωi=Mi-miεb-a болады, мұнда
mi=inffx, Mi=supfx.
{xi,xi+1} {xi,xi+1}
Олай болса, бүкіл қисық у = fx мына [xi,xi+1; mi, Mi] (i=0,1,2,...,n-1) тік төртбұрыштардан тұратын фнгурамен айнала қоршалынады және
P-p=i=0n-1Mi-mixi+1-xi=i=0n-1ωi∆xi εb-a∙b-a=ε.
Сонымен, у = fx теңдеумен кескінделген үздіксіз қисықтың ауданы нө льге болатын болды.
Енді параметрлік теңдеулермен берілген қисықты қарайық:
x=φt, y=ψ(t)
α=t=β
Егер φt және ψt функцияларының бүкіл [α,β] аралығында үздіксіз φʼt жэне ψʼt туындылары болса, бұл параметрлік теңдеулермен берілген сызықты біртегіс қисық деп атайды. Осы тұжырымдалған сөйлемді геометрия тілімен былай айтуға болады: әрбір нүктесінде бағытын үздіксіз өзгертіп отыратын жанамасы бар қисықты біртегіс қисық деп атайды.
Егер біртегіс қисықтұйық болса, онда
φʼα=φʼβ, ψʼα=ψʼβ болады.
Біртегіс қисықтың ауданы да нөль болады.

1.2. Жазық фигуралардың ауданын интеграл арқылы
өрнектеу
1. Жоғарғы жағынан у = fx теңдеумен берілген үздіксіз қисықпен, төменгі жағынан X осімен, ал бүйір жақтарынан х = a және х = b түзулермен қоршалған жазық фигураның ауданын қалай табуды біз білеміз. Мұндай фигураның ауданы тең болады (1-чертеж):

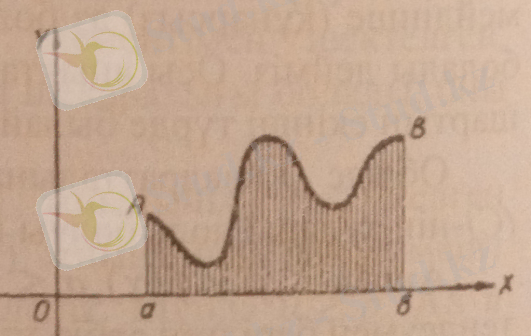
U=abfxdx=abydx. (2)
Егер фигура жоғарғы жағынан y=f1x, (a=x=b) қисықпен, төменгі жағынан y=f2x, (a=x=b) қисықпен бүйір жақтарынан х = а түзулермен қоршалған болса, мұндай фигураның ауданы былай өрнектеледі:
U=ab[f1x-f2x]dx. (3)
Фигураны жоғарғы жағынан қоршап тұрған қисық параметрлік теңдеулермен берілсін:
x=φt,
y= ψt. (α = t = β) (1)
Мұнда біз φt, ψt және φʼt функцияларын [α, β] аралығында үздіксіз, ал және ψt,φʼt функцияларын (α, β) интервалында оң деп ұйғарамыз. Одан басқа φα=a, ψβ=b болуы қажет.
Айнымалы параметр t α -ден β -ға дейін үздіксіз өзгергенде абсцисса x=φ(t) a-дан b-ге дейін өсуі керек.
Мұндай фигураныц ауданы (2) формуламен анықталады деп біз жоғарыда айттық. Айнымалы параметр t-нің а-дан β-ға дейін өсуімен бірге x=φ(t) функция да а-дан b-ға дейін үдейтін болғандықтан, (2) интегралдағы айнымалы х-ті ауыстыруға әбден болады. Сөйтіп, фигураның ауданы
U=αβψtφʼtdt. (4)
болады.
Егер (α, β) интервалында функция ψt оң болып, ал туынды φʼt теріс болса және φα=b, ψβ=a, онда параметр а-дан β-ға дейін өскенде, функция x=φ(t) b-ден а-ға дейін кемиді, Бұл жағдайда фигураның ауданы:
U=αβψtφʼtdt. (5)
болады.
Сонымсн,
U=+-αβψtφʼtdt. (6)
Егер параметр t мен абсцисса х бір бағытта өзгеретін болса, онда интеграл таңбасы алдында плюс алынады, ал егер олардың өзгеру бағыты бір-бірімен карама-қарсы болса, онда иитеграл алдына минус таңбасы алынады.
2. Енді тұйық сызықпен қоршалған фигураның ауданын қарайық. Егер фигуранын контуры (К) координаталар осьтеріне параллель түзулермен екі-ак нүктеде (одан артық емес) қиылысатын болса. онда мұндай фигуранын ауданын табу үшін қисықка у осіне параллель етіп АР және жанамаларды жүргіземіз. Сонда фигураны қоршап тұрған контур (К) екіге бөлінеді: біреуі АСВ, оның кез келген ординатасын у1 деп, екіншісі АDВ, оның кез келген ординатасын у2 арқылы белгілейік (2-чертеж). Былай ұйғарайық:

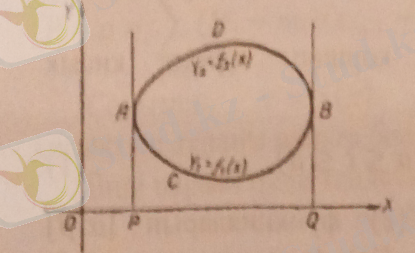
ОР = а, OQ = b, b a.
Қарастырып отырған фигураның ауданы мына формуламен
U=aby2-y1dx.
өрнектелетінін 80-чертеждің өзінен-ақ көрініп тұр, Мұнда у1 мсн у2 қисықтың мына түрде
F(х, у) = 0 (6')
берілген теңдеуінен табуға болады. Ол үшін бұл теңдеуді у бойынша шешу керек. Келесі екі теңдеу системасын
F(х, у) = 0 (7)
ә F(х, у)ә у= 0
х бойынша біріктіріп шешіп а мен b-ні табамыз.
Көбінесе (6') теңдеуді у бойынша тікелей шешу мүмкін болмай қалады. Сондықтан фигураны қоршап тұрған контурдың теңдеуін (6') түрде қарау әрқашан ыңғайлы бола бермейді.
Фигураны қоршап тұрган контур (К). координаталар осьтсріне параллсль түзулермен екіден артық нүктелерде қиылысатын жағдайды қарайық (3 -чертеж).

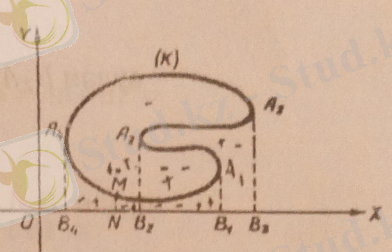
Контурдың теңдеуі параметрлік түрде (1) теңдеулермен берілсін.
φt, ψt функциялар жөнінде келесі ұйғаруларды жасаймыз:
1) φt және ψt, аралығында үздіксіз және осы аралықта үздіксіз туындылары бар функциялар;
2) Параметр t t0- ден T-ге дейін өзгергенде нүкте [φt, ψt] контурды бір ғана рет оң бағытта әліптейді, ягни контурмен қоршалынған облыс D қозғалыс бағытына қарағанда сол жақта қалып қойып отырады;
3) туындылар φˈt және ψˈt бірнеше рет қана нольге айналады.
Кейінгі ұйғаруды мына мағынада түсінуге болады: параметр t -нің тек мына екі t0 және Т мәндерінен басқа әр түрлі мәндеріне контур (К)-ның әр түрлі нүктелері сәйкес келеді және
φt0=φT.
ψt0=ψt.
Контурдың М нүктесі параметрдің t0 жэне Т мәндеріне сәйкес келсін. Контурды бірнеше MA1, A1A2, A2A3, A3A4, A4Μ доғаларға бөлейік. Осы доғалардың бойында функция ψt біркелкі өзгеретін болсын. A1,A2, A3,A4 нүктелерге сәйкес келетін параметр t-нің мәндері t1,t2,t3,t4 мына тәртіппен
t0 t1t2t3t4T
орналассын.
Жоғарыда келтірілген (6) формулаға сүйене отырып мыналарды табамыз:
аудан NM A1 B1=t0t1ψtφˈtdt,
аудан B2 A2 A1 B1=-t1t2ψtφˈtdt,
аудан B2 A2 A3 B3=t2t3ψtφˈtdt,
аудан B4 A4 A3 B3=-3t4ψtφˈtdt,
аудан B4MAN=t4Tψtφˈtdt.
Егер осы теңдіктерді қоссақ, сонда іздеп отырған аудан шығады:
U=-t0Tψtφˈtdt. (8)
Егер фигура толығымен немесе жартылай X осінің төменгі жағында жататын болса, онда координаталардың бас нүктесін көшіріп, облысты X осінің жоғарғы жағында жататындай жағдайға келтіреміз.
х пен у-тің рөлін ауыстырып, фигураның ауданын былай өрнектеуге де болады:
U=+t0Tψtφˈtdt. (9)
(8) және (9) формулаларды бір-бірімен қосып, төмендегі формулаларды табамыз:
U=12tT[φ(t)ψˈt-ψtφˈt]dt. (10)
немесе
U=12tT(xdy-ydx). (10')
Мысал келтірейік.
1-мысал. Астроиданың ауданын табу керек.
Астроида деп төмендегі параметрлік теңдеулермен
x=acos3t
y=asin3t
берілген қисықты айтады (4-чертеж). (5) формуланы қолданып табамыз:
U=-40PI2asin3t∙3acos2t∙sintdt=-12a2 0PI2sin4t∙cos2tdt=-12a20PI2sin4tdt+ +0PI2sin6tdt=-(-3∙14∙2∙PI2+5∙3∙16∙4 ∙2∙PI2)∙12a2=38PIa2.
2-мысал. Декарт жапырағы тұйық бөлігінің ауданын табу керек. Декарт жапырағы деп мына
x3+y3=3axy (11)
теңдеумен берілген қисықпен қоршалған фигураны айтады (4- чертеж).

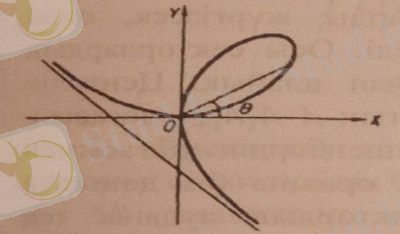
Бұл ауданды табу үшін (11) теңдеуді параметрлік түрге көшіру керек. Параметр t үшін θ бұрышының тангенсін аламыз, яғни t = tg θ мұнда θ бұрышы 0-ден PI2 - ге дейін өзгереді, олай болса, параметр t 0-ден infinity-ке дейін өзгереді. Мұнда tgθ=yx= t, бұл арадан y=tx.
у-тің осы мәнін (11) теңдеуге апарып қойып табамыз:
x3+t3x3=3ax2t,
бұл арадан
x=3at1+t3; y=3at1+t3
Енді (10) немесе (10ʹ) формуланы қолданамыз:
dx=3a∙1-2t3(1+t3)t2dt; dy=3a∙2t-t4(1+t3)t2dt
U=9a220infinityt2t-t4-t2(1-2t3)(1+t 3)3dt=9a220infinityt2dt1+t32=-3a221 1+t2=32a2.
3. Сектор деп бір үздіксіз АВ қисықтың доғасымен, екі ОА және ОВ радиус-векторлармен қоршалған фигураны айтады (5-чертеж). Қисық АВ поляр координаталарда мына

ρ=f(θ)
теңдеумен берілсін.
α және β, ОА мен ОВ радиус - векторлардың поляр осьпен жасайтын бұрыштары болсын.
fθ[α,β] аралығында берілген оң және үздіксіз функция.
α мен β - ның арасындағы мына мәндерді алып:
α=θ0θ1θ2 ∙ ∙ ∙ θiθi+1 ∙ ∙ ∙ θn-1θn=β,
осы бұрыштарға сәйкес радиус-векторларды жүргізсек, онда сектор ОАВ п бөлшек секторларға бөлінеді. Осы секторлардың ішінен біреуін, мәселен ОАіАі+1 секторын алайық. Центрлік ∆θ=θi+1-θi бұрышын өзгертпей қисықтың A AiAi+1 доғасын, радиусы мына санға OAi=f(θi) тең шеңбердің доғасымен ауыстырайық. Сонда OAiАі+1 сектордың орнына біз дөңгелек секторы OAiВi - ді аламыз. Дөңгелек сектордың ауданы тең болады:
12f2θi∆θi.
Осындай дөңгелек секторлардың саны п -1 және олардың аудандарының қосындысы болады:
12i=0n-1f2θi∆θi. (12)
(12) қосынды ОАВ сектордың ауданының жуық мәнін береді, оның дәл мәнін табу үшін барлық ∆θi-лерді нольге ұмтылтып, қосындыдан шек аламыз. Бұл қосынды интегралдық қосынды және оның шегі бар, өйткені fθ -- үздіксіз функция.
Сонымен, сектордың ауданы мынадай болады:
U=12αβf2θdθ=12αβp2dθ. (13)

Мысал. Мынадай теңдеумен
Ax2+2Bxy+Cy2 (AC-B20, C0)
берілгеи эллипстің ауданын табу керек.
Поляр координаталарды енгізіп, яғни мына қатыстарды:
x=ρcosθ
y=ρsinθ
пайдаланып, эллипстің берілген теңдеуін мына түрге келтіреміз:
ρ2=1Acos2θ+2Bsinθcosθ+Csin2θ.
Енді (13) формуланы қолданып табамыз:
U=4∙120PI2dθAcos2θ+2Bsinθcosθ+Csin2 θ=20PI2dtgθCtg2θ+2Btgθ+A=PIAC-B2.

1.3. Доғаның ұзындығы

1. Қисықтың доғасының ұзындығы деп нені айтады, алдымен соған түсінік берейік.
AB- жазықтықта жатқан бір қисық сызық болсын. Оның ұзындығының анықтамасын беру мақсатымен AB доғасын п бөлікке бөлеміз, A=A0,A1,A2, ... An-1,An=B бөлу нүктелері болсын. Осы бөлу нүктелері арқылы A0,A1,A2, ... An-1,An кесінділерін жүргізіп, қисыққа іштей сызылған сынық сызық шығарамыз (6-чертеж). Жаңағы жүргізілген кесінділерді сынық сызықтың звенолары деп атайды.

Егер осы звенолардың саны шексіздікке ұмтылып, әрбір звеноныц ұзындығы нольге ұмтылғанда сынық сызықтың ұзындығы бір тиянақты шекке ұмтылса, ол шекті АВ доғасының ұзындығы деп атайды.
Осы айтылған шек әрбір қисық үшін бола бермейді, олай болса әрбір қисықтың ұзындығы бола бермейді.

Егер қисықтың ұзындығы болса, онда қисықты түзетілетін қисық деп атайды.
Қисық АВ, ХОУ жазықтығында у = f(х) теңдеумен берілсін. Мұнда f(х)[ а,b ] аралығында анықталған үздіксіз және үздіксіз fʹ(х) бар функция.
Бөлу нүктелерінің абсциссалары мына сандар x0, x1, x2,x3, ..., xn-1,xn болсын. Бүл сандардың орналасу тәртібі былай:
a=x0x1x2 ∙ ∙ ∙ xn-1xn=b.
Сынық сызықтың бір номерлі звеносының үзындығы болады:
(yi+1-yi)2+(xi+1-xi)2=[fхi+1-fхi]2+ (xi+1-xi)2.
Бұл сынық сызықтың өзінің үзындығы барлық звенолардың үзындықтарының қосындысына тең:
σ=i=0n-1[fхi+1-fхi]2+(xi+1-xi)2.
Квадрат жақшаның ішінде тұрған айырмаға щекті өсімше жөніндегі Лагранж теоремасын қолданайық:
fхi+1-fхi=xi+1-xifʹξi,
xiξixi+1.
(13) қосынды - интегралдық қосынды.
Анықтама бойынша қисықтың доғасының үзындығы S, (13) қосындының шегіне тең, яғни
S=limi=0n-11+fʹ2(ξi)∙xi+1-xi.
max⁡xi+1-xi--0
немесе
S=ab1+fʹ2(x)dx=ab1+(dydx)2dx. (14)
Егер қисықтың теңдеуі мына түрде берілсе:
x=gy, c=y=d,
мұнда с мен d - А мен B - нің ординаталары. gy -- [с, d] аралығында берілген, осы аралықта үздіксіз және у бойынша үздіксіз туындысы gʹy бар функция. Мұндай қисықтың доғасының ұзындығы былай өрнектеледі:
S=cd1+gʹ2(y)dy=ab1+(dxdy)2dy.
1 - мысал. Мынадай теңдеумен x2=2ρy берілген парабола доғасының ұзындығын мына шекаралықта: 0=x=b есептеп шығару керек
Берілген теңдеуден
y=x22p; yʹ=xp.
(14) формула бойынша
S=0b1+x2p2dx=1p0bp2+x2dx=1px2p2+x2+ p22lnx+p2+x2b0=12pbb2+p2+p2lnb+b2+ p2-p2lnp.
2. AB қисығының бір нүктесі, мәселен A(x0,y0) қозғалмайтын болсын да, ал екінші нүктесі M(x,y) доғаның бойымен үздіксіз қозғалатын болсын. Онда MA доғаның ұзындығы х пен у-ке тәуелді айнымалы шама болып табылады. Ал х пен у өзара мына y=fx немесе x=g(y) теңдеу арқылы байланысты болғандықтан, MA доғаның ұзындығы тек бір ғана х-тің немесе у-тің ғана функциясы болады.
Сөйтіп, қисықтың теңдеуі қай түрде берілді: мына түрде ме y=fx, жоқ мына түрде ме x=g(y), міне соған байланысты
Sx=ax1+(dydx)2dx, (15)
немесе
Sy=ay1+(dxdy)2dy. , (16)
(15) теңдікті x бойынша, ал (16) теңдікті y бойынша дифференциалдан табамыз:
dSdx=1+(dydx)2,
dSdy=1+(dxdy)2.
Бәрібір осы екі жағдайдың екеуінен де мына формула келіп шығады:
dS=dx2+dy2. (17)
dS шаманы доғаның дифференциалы деп атайды.
(17) формуланы доғаның дифференциалының формуласы дейді.
3. Енді қарастырып отырған қисық параметрлік теңдеулермен берілсін
x=φt.
y=ψt. (1)
Мұнда φt және ψt -- [α,β] аралығында үздіксіз және осы аралықта үздіксіз φʹt,ψʹt туындылары бар функциялар деп ұйғарамыз. Туындылар φʹt және ψʹt бір уақыттың ішінде нольге айналып кетпейді. Олай болса, бір кішкентай (t0-δ,t0+δ) аймақта не φt, не ψt біркелкі болады.
(17) формуланы қолданып табамыз:
(dS)2=φʹ2tdt2+ψʹ2tdt2,
немесе
dS=φʹ2t+ψʹ2tdt.
α-дан β-ға дейін интералдан табамыз:
S=α βφʹ2t+ψʹ2tdt=αβ(dxdt)2+(dydt)2dt. (18)
2-мысал. Төмендегі параметрлік теңдеулермен
x=a(t-sint,)
y=a(1-cost) 0=t=2PI
берілген циклоиданың бір арқасының ұзындығын табу керек. Бұл есепті шығару үшін (18) формуланы қолданамыз:
dxdt=a1-cost; dydt=asint;
(dxdt)2+(dydt)2=2a21-cost=4a2sin2t2 .
S=2a02PIsint2dt=-4acost2=8a.
4. Енді қисықтыңтеңдеуі поляр координаталарда берілсін:
p=fθ,
мұнда fθ[θ0,θ1] аралығында үздіксз және осы аралықта θ бойынша үздіксіз fʹθ туындысы бар функция.
Қисық нүктелерінің декарпық координаталар мен поляр координаталарының арасындагы мына қатынастарды
x=pcosθ, y=psinθ
немесе
x=fθcosθ, y=fθsinθ.
аналитикалық геометриядан білеміз.
Кейінгі екі теңдеуді қисықтың параметрлік теңдеулері деп қараймыз. Мұнда параметр θ.
(18) формуланы пайдаланамыз:
dxdθ=cosθdpdθ-psinθ,
dydθ=sinθdpdθ+pcosθ,
бұл арадан
(dxdθ)2+(dydθ)2=p2+(dpdθ)2
S=θ0θ1p2+(dpdθ)2dθ. (19)
Бұл системада доғаның дифференциалы
dS=(dp)2+p2(dθ)2 (20)
болады.
3-мысал. Төмендегі теңдеумен p=a(1+cosθ) берілген кардиоиданың үзындығын есептеп шығару керек (7-чертеж).

Бұл есепті шығару үшін (19) формуланы қолданамыз.
S=2a0PI(1+cosθ)2+sin2dθ=2a0PI2(1+co sθ)dθ=4a0PIcosθ2dθ=8asinθ2PI0=8a.

1.4. Денелердің көлемін анықталған интеграл арқылы өрнектеу

1. Дененің колемін табу туралы есеп еселік интегралдардың ғана көмегімен толық шешіледі. Қазір біз кейбір жағдайлардьп ғана қараймыз.
Үш өлшемді кеңістікте, тұйық бетпен қоршалған кез келген формалы дене берілсін (8-чертеж).

Дененің бі р нүктесі арқылы, Х осіне перпендикуляр етіп жазыктық жүргізсек, онда денеде көлденең қима пайда болады. Осы көлденең қима квадратталынатын фигура болсын. Егер оның ауданын и деп белгілейтін болсақ, онда бұл аудан айнымалы х-тің функциясы болады: и -- и(х). х = а және х = b мәндерге сәйкес келетін екі қиманың арасындағы дененің көлемін есептеп шығарайық. Ол үшін X осіндегі а-дан ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.