Анықталған интегралдарды жуықтап есептеу

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 18 бет
Таңдаулыға:

Қостанай мемлекеттік педагогикалық институты

Жаратылыстану-математика факультеті

Физика-математика және жалпы техникалық пәндер кафедрасы

Тағабай Әділ Қайратұлы

Анықталған интегралдарды жуықтап есептеу

Курстық жұмыс

Ғылыми жетекші:Доспулова У. К.

аға оқытушы

Қостанай, 2015ж

Мазмұны

Кіріспе . . . 3

Лагранждың интерполяциялық полиномы . . . ……. …. 5
Анықталған интегралдарды жуықтапесептеу жолдары…… . . . …… . . . 6Тікбұрыштар тәсілі . . . 6Трапециялар тәсілі . . . 7Симпсон формуласы . . . 8Котес формуласы . . . 9
Жуықтап есептеуде жіберілген қатенің мөлшерін табу . . . 13

Практикалық бөлім . . . 14

Қорытынды . . . 17

Қолданылған әдебиеттер тізімі . . . 18

Кіріспе

Анықталған интеграл ертеректе жазық фигуралардың ауданын табу негізінде туындады. Ал қазір анықталған интеграл барлық техникалық ғылымдардағы аз шаманың үлкен сандарының қосындысын табуға арналған есептерді шешуде қолданылады. Анықталмаған интеграл интеграл(лат. іnteger - бүтін) - математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан - туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады. «Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған; өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама. Біз бұл курстық жұмыста білімнің әр түрлі саласына жататын, бірақ екеуінің де шешуін табу бір математикалық аппаратқа негізделген екі есепті қарастырмақшымыз. Сөз болып отырған математикалық аппарат бірінші қарағанда функцияларды дифференциалдау мен интегралдау мәселесіне тура қатысы жоқ сияқты болып көрінеді.
Тарихта да ұзақ уақыттар бойы бұл аппарат дифференциалдау
және интегралдау операцияларымен байланыссыз өсіп дамыған.

XVII ғасырдың аяғында-ақ бұл циклдегі есептерді шешудің ең
күшті және ең жалпы әдісін оларды интегралдық есептеуде
шешілетін мәселелермен байланыстыру жолында ғана жасауға
болатыны анық болды.

Біздің қарастырмақ болып отырған есептеріміздің бірі жазық фигуралардың ауданын есептеп шығару.

Элементарлық геометрияда тек түзу сызықты кесінділер және
шеңбер доғаларымен шенелген жазық фигуралардың аудандарын
есептеп шығару әдісі беріледі. Кез келген қисық сызықпен шенел-
ген жазық фигураныңа ауданын табу жөніндегі жалпы
геометриялық мәселені тек математикалық анализдің
құралдарының жәрдемімен ғана шешуге болады. Кез келген
жазық фигураның ауданын есептей білудің теориялық және
ешқандай арнайы ыспаттауды керек етпейді.

Зерттеудің өзектілігі: курстық жұмыстың мазмұнының ғылыми құндылығын арттыру және оның негізінде пәнге деген қызығушылығын арттырып, өз бетінше іздену. Білім, білік, дағды алуын қамтамасыз етуге, жеке шығармашылық қабілеті дамуы үшін жағдай туғызу.

Мақсаты: Анықталған интегралды жуықтап есептеудің әдістерін зерттеу .

Міндеті:

-Анықталған интегралды жуықтап есептеуді дәлелдеу және талдау.

-Анықталған интегралды жуықтап есептеу бойынша есептер мен мысалдар.

Зерттеу объектісі: Математикалық талдау.

Зерттеу пәні: Анықталған интегралды жуықтап есептеу әдістерін қолдану

Зерттеу әдістері: Талдау нәтижесінде алынған мәліметтерді бақылап, тақырып бойынша әдебиеттерді зерттеу

Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, практикалық жұмыс, қорытынды және қолданылған әдебиеттер тізімінен тұрады.

1. Лагранждың интерполяциялық полиномы

Айталық, f(x) - [ a, b ] аралығында берілген бір функция.
$\varepsilon$ -алдын ала берілген оң құнарсыз аз сан болсын.

Енді мәселені былай қоялық:

[ а, b ] аралығындағы барлық х-тер үшін төмендегі шартты

$\left f(x) - \varphi(x) \right < \varepsilon$ қанағаттандыратын, f (х) -тен гөрі жабайырақ басқа бір $\varphi(x)$
функциясын табуға бола ма?

Егер мұндай функцияны табуға мүмкін болса, онда функция
$\varphi(x), f(x)$ функцияның дәлдігі $\varepsilon$ -ге дейін жуық мәнін береді.
Кейбір жағдайда функция $\varphi(x)$ функция f(х) -тің тек жуық мәнін
ғана беріn қоймайды, $\varphi(x)$ -тің қасиеті бойынша f(х) -тің қасиетін
білуге болады.

Берілген f(x) функциясын, [ а, b ] аралығында n дәрежелі
көпмүшемен де кескіндеуге болады. Мүндай полином (көпмүше)
үшін, [ а, b ] аралығының алдын ала берілген нүктелерінде f(x)
функциясымен дәлме-дәл келетін полиномды алуға болады.
Мұндай полиномның коэффициенттерінің саны n + 1 , сондықтан
оны табу үшін, оның мәндерін [ а, b ] аралығының n +1
нүктелерінде беру керек.

Сонымен, бұл жөніндегі есепті мына түрде қоюға болады:
берілген функция f(x) үшін [ а, b ] аралығының мына
нүктелерінде $x_{0}, \ x_{1}, \ x_{2}$ _, $x_{2}$ _………., ${\ x}_{n}$ мынадай мәндерді

$y_{0} = f\left( x_{0} \right), y_{1} = f(x_{1})$ , ………, $y_{n} = f(x_{n})$

қабылдайтындай, дәрежесінен жоғары емес полином Р (х) - ті
табу керек.

Мұндай есепті интерполяциялау есебі деп атайды.
Интерполяциялау полиномын мына түрде алуға болады:
P(x) = $\frac{\left( x - x_{1} \right) \left( x - x_{2} \right) \ \ldots. \ \ \left( x - x_{n} \right) }{\left( x_{0} - x_{1} \right) \left( x_{0} - x_{2} \right) \ldots. . \ \left( x_{0} - x_{n} \right) }f\left( x_{0} \right) + \frac{\left( x - x_{0} \right) \left( x - x_{2} \right) \ \ldots\ \left( x - x_{n} \right) }{\left( x_{1} - x_{0} \right) \left( x_{1} - x_{2} \right) \ \ldots\ \left( x_{1} - x_{n} \right) }f(x) + \ldots + \frac{\left( x - x_{0} \right) \left( x - x_{1} \right) \ \ldots\ \left( x - x_{n} - 1 \right) }{\left( x_{n} - x_{0} \right) \left( x_{n} - x_{1} \right) \ \ldots\ \left( x_{n} - x_{n - 1} \right) }f(x)$

Бұл полиномды Лагранждыц интерполяциялау полиномы деп
атайды.

Лагранждың интерполяциялық формуласына бір мысал
келтірейік:

х = 1 болғанда 5-ке тең , х = 2 болғанда 13-ке тең және х = 5
болғанда 17-ге тең мәндерді қабылдайтын екі дәрежелі көпмүшені
табу керек.

n = 2, Лагранж формуласы бойынша

y = P(x) =5 $\frac{(x - 2) (x - 5) }{(1 - 2) (1 - 5) } + 13\ \frac{(x - 1) (x - 5) }{(2 - 1) (2 - 5) } + 17\frac{(x - 1) (x - 2) }{(5 - 1) (5 - 2) } = \ - \frac{5}{3}x^{2} + 13x - \frac{19}{3}.$

2. Анықталған интегралдарды жуықтапесептеу жолдары

2. 1. Тікбұрыштар тәсілі

Механика, физика және техниканың көп мәселелері дәл
мәнін табу мүмкін емес анықталған интегралдарға келтіріледі.
Мұндай интегралдарды есептеп шығару үшін жуық
формулаларды жасауға тура келеді. Бұл формулалардың саны өте
көп. Бірен-сараны ғана болмаса, олардың бәрін бірдей көрсету
мүмкін емес.

Мына

$\int_{a}^{b}{f(x) dx}$

анықталған интегралдың мәнін табу керек, мұнда f(x) - [ а, b ]
аралығында берілген үздіксіз функция. Егер интеграл астында

тұрған функцияның алғашқы функциясы белгілі болса, онда
Ньютон-Лейбниц формуласы бойынша бұл интегралдың дэл
мәнін таnқан болар едік. Бірақ тәжірибелік есептерде кездесетін
көп интегралды көрсетілген формула негізінде есептеn шығару
мүмкін емес, өйткені алғашқы функциялары элементар
функциялар арқылы өрнектелетін интегралдардың саны тіnті
шамалы. Сондықтан, көбінесе анықталған интегралдардың жуық
мәнін іздейді. Мұның бірнеше жолдары бар. Олардың біреуі
мынау: [ а, b ] аралығын бірдей етіn n бөлшек сегменттерге
бөлейік, сонда $\mathrm{\Delta}x_{i} = \ x_{i + 1} - x_{i} = \frac{b - a}{n}$ және интегралдық қосынды
мына түрде болған болар еді:

$\sigma = \frac{b - a}{n}\left\lbrack f(\xi_{0}) + f(\xi_{1}) + \ldots + f(\xi_{n - 1}) \right\rbrack.$

Сонда аныкталған интегралдың жуық мәні
$\int_{a}^{b}{f(x) dx} \approx \frac{b - a}{n}\left\lbrack f(\xi_{0}) + f(\xi_{1}) + \ldots + f(\xi_{n - 1}) \right\rbrack$ (1)

болады.

(1) формуланың геометриялық мағынасы айқын (74-чертеж) .

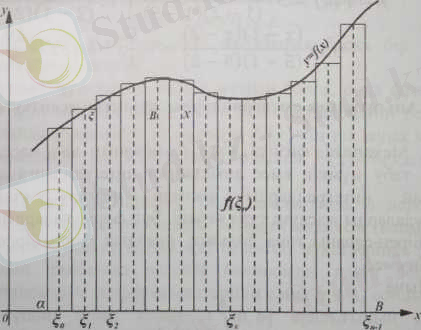
74-чертеж

(1) Формуланы тік төртбұрыштар формуласы деп атайды.

Тәжірибе жүзінде $\xi_{i} -$ ді мынаған теңеп $\xi_{i} = \frac{x_{i} + x_{i + 1}}{2} = x_{i} + \frac{1}{2}$ алады. $D:\..\AppData\Local\Temp\FineReader12.00\media\image2.jpeg$

2. 2. Трапециялар тәсілі

Анықталған интегралдың мәнін табу, геометрия тілімен
айтқанда, жоғарғы жағынан f(х) функцияның графигімен,
төменгі жағынан[ а, b ] кесіндісімен, бүйір жақтарынан

х = а және х = b түзулермен қоршалған фигураның ауданын табу
деген мэселе екенін біз жоғарыда жеткілікті түрде айттық.

Мүндай фигураның ауданын табудың бір жолы мынау:

[ а, b ] аралығын бірдей етіn бірнеше бөлшек сегменттерге
бөлеміз. Бөлу нүктелері a = $x_{0}, x_{1}, x_{2}, \ \ldots, x_{n - 1} = b$ болсын.

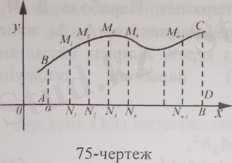
Осы бөлу нүктелері арқылы қисықтың өзімен

түйіскенше ординаталар жүргіземіз де, сонан соң олардың ұштарын бір-бірімен қосамыз. Сонда қисыққа іштейсызылған сынық сызық келіп

шығады(75-чертеж) .

Бастапқы айтылған фигура
ауданының орнына, сынық сызық-
пен қоршалған фигураның ауданын алады. Ал бүл кейінгі
фигураның ауданын алады. Ал бүл кейінгі фигураның ауданы n
траnециялардың аудандарының қосындысына тең. Траnеция-

лардың аудандарының қосындысы

$\frac{1}{2}\left( y_{0} + y_{1} \right) h + \frac{1}{2}\left( y_{1} + y_{2} \right) h + \frac{1}{2}\left( y_{2} + y_{3} \right) h + \ldots + \frac{1}{2}\left( y_{n - 1} + y_{n} \right) h = \left( \frac{1}{2}y_{0} + y_{1} + y_{2} + \ldots + y_{n - 1} + \frac{1}{2}y_{n} \right) h$ болады, мүнда h = $\frac{b - a}{n}$ .

Сонымен, іздеп отырған анықталған интегралдың жуық мәні

мына төмендегідей болады:

$\int_{a}^{b}{f(x) dx \approx} = \frac{b - a}{n}\left( \frac{1}{2}y_{0} + y_{1} + y_{2} + \ldots + y_{n - 1} + \frac{1}{2}y_{n} \right) = \frac{b - a}{n}\left\lbrack \frac{1}{2}f\left( x_{0} \right) + f\left( x_{1} \right) + f\left( x_{2} \right) + \ldots + f\left( x_{n - 1} \right) + \frac{1}{2}f\left( x_{n} \right) \right\rbrack. (2)$

Бүл формуланы траnециялар формуласы деп атайды.

Осы формула арқылы кез келген анықталған интегралдың
жуық мәнін интеграл ішінде түрған функцияның дербес мәндері
бойынша табуға болады.

Мұнда бір айта кететін мәселе мынау: неғұрлым n саны көп
болған сайын, соғұрлым интегралдың мәні дәлірек болады.

2. 3. Симпсон формуласы

Енді алғашқыда айтылған фигураның ауданын табу үшін,
әрбір ординаталар үштарының арасындағы қисықтың доғасын, осі
у осіне nараллель парабола доғасымен ауыстырамыз.

Осьтердің бағытын өзгертпей, координаталардың бас нүктесін
а нүктесіне көшірейік.

Осі у осіне параллель айтып отырған параболаның теңдеуі
мына түрде болсын:

y = $A_{0} + A_{1}x + A_{2}x^{2}$ (3)

Осы парабола В, М ₁ және М ₂ нүктелер арқылы өтетін болсын,
бүл параболамен ВМ ₂ догасын ауыстырамыз. Парабола В, М ₁ және М ₂ нүктелер арқылы өту үшін, коэффициенттер $A_{0}, A_{1}$ және
А ₂ қандай болу керек, соны табуымыз керек. Жаңағы айтылған
нүктелердің координаталары (3) параболатеңдеуін
қанағаттандыруы керек, сондықтан:

$y_{0} = A_{0},$

$y_{1} = A_{0} + A_{1}h + A_{2}h^{2},$

${\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ y}_{2} = A_{0} + {2A}_{1}h + {4A}_{2}h^{2}$ (4)

(3) параболамен, х осімен және ОВ, $N_{2}$ М ₂ ординаталармен
қоршалынған фигураның ауданы

$\int_{0}^{2h}{ydx} = \int_{0}^{2h}{\left( A_{0} + A_{1}x + A_{2}x^{2} \right) dx = 2A_{0}h + {2A}_{1}h^{2} + \frac{{8A}_{2}h^{3}}{3} = \frac{h}{3}\left( 6A_{0} + {6A}_{1}h + 8A_{2}h^{2} \right) ^{2}}$

болады.

Егер (4) теңдеулерді еске алсақ, онда

$\int_{0}^{2h}{ydx} = \left( y_{0} + {4y}_{1} + y^{2} \right) \frac{h}{3}$ (5)

[ а, b ] аралығын бөлшек сегменттерге бөлу саны n = 2m жұn
болсын.

Жаңағы көрсетілген жолмен келесі $N_{2}M_{2}M_{4}N_{4}$ фигураның
ауданын табамыз:

${N_{2}M_{2}M_{4}N_{4}}_{ауд}$ = $\left( y_{2} + {4y}_{3} + y_{4} \right) \frac{h}{3}$ (6)

Міне, осылай етіп әрі қарай соза береміз. Сонда іздеп отырған
фигураның ауданының жуық мәні мынау:

$\int_{a}^{b}{f(x) dx \approx \frac{h}{3}\left( y_{0} + {4y}_{1} + {2y}_{2} + {4y}_{3} + {2y}_{4} + \ldots + {4y}_{2m - 1} + y_{2m} \right) } = \frac{1}{3}\frac{b - a}{2n}\left\lbrack {f(x}_{0}) + 4f\left( x_{1} \right) + 2f\left( x_{2} \right) + \ldots + 4f\left( x_{2n - 1} \right) + f(x_{2n}) \right\rbrack$ (7)

Бұл формуланы Симnсон формуласы деп атайды.

Симпсон формуласы, бұдан бұрынғы формулаларға
қарағанда, дәлірек нәтиже береді.

2. 4. Котес формуласы

Енді Лагранждың интеполяциялық полиномын
пайдаланып, анықталған интегралдардың жуық мәнін табуға
болады, соған біраз тоқтап кетейік.

Айталық, бізге мына анықталған интеграл

$\int_{a}^{b}{f(x) dx}$

берілсін. Осы интегралдағы айнымалыны былай ауыстырсақ:

x=a+(b-a) t,

онда

$\int_{a}^{b}{f(x) dx} = (b - a) \int_{0}^{1}{f\left\lbrack a + (b - a) t \right\rbrack dt. }$

Бастапқы берілген анықталған интегралды осылай түрлендіру,
- координаталардың бас нүктесін а нүктесіне көшірумен парапар.

[ a, b ] аралығын бірдей етіn n бөлшек сегменттерге бөлейік.
Сонда бөлу нүктелерінің абсциссалары мынадай болады:
$x_{0} = a, x_{1} = a + h,$

$x_{2} = a + 2h, \ldots, x_{n - 1} = a + (n - 1) h, \ x_{n} = b$

ал бұларға сәйкесті t-нің мәндері:

$t_{0} = 0, \ \ \ \ \ \ t_{1} = \frac{1}{n}, \ t_{2} = \frac{2}{n}, \ \ldots\ \, t_{n - 1} = \frac{n - 1}{n}, t_{n} = 1.$

f(x) функция графигінің жоғарыдағы нүктелерге сәйкес
келетін ординаталары:

$y_{0} = f\left( x_{0} \right), \ y_{1} =$ ( $x_{1}), \ \ldots\ \, y_{n - 1} = f\left( x_{n - 1} \right), \ y_{n} = f(x_{n})$

Енді у = f(x) қисықтың орнына мына төмендегі теңдеумен

Y= $A_{0} + A_{1}x + A_{2}x^{2} + \ldots\ + A_{n}x^{n}$
кескінделетін және берілген қисықтың жоғарыда көрсетілген
n + 1 нүктесі арқылы өтетін қисықты аламыз.

Лагранж формуласы бойынша:

y= $y_{0}\frac{\left( t - \frac{1}{n} \right) \left( t - \frac{2}{n} \right) \ldots\ (t - 1) }{\left( 0 - \frac{1}{n} \right) \left( 0 - \frac{2}{n} \right) \ldots\ (0 - 1) } + y_{1}\frac{(t - 0) \left( t - \frac{2}{n} \right) \ldots\ (t - 1) }{\left( \frac{1}{n} - 0 \right) \left( \frac{1}{n} - \frac{2}{n} \right) \ldots\ \left( \frac{1}{n} - 1 \right) } + \ldots + y_{n}\frac{(t - 0) \left( t - \frac{1}{n} \right) \ldots\ \left( t - \frac{n - 1}{n} \right) }{(1 - 0) \left( 1 - \frac{1}{n} \right) \ldots\ \left( 1 - \frac{n - 1}{n} \right) }$ (5)

y=f(x) қисықпен қоршалынған ауданның орнына, (5)

қисықпен қоршалған ауданды алсақ, сонда
$\int_{a}^{b}{f(x) dx \approx (b - a) \int_{0}^{1}{ydt}}$

Немесе

$\int_{a}^{b}{f(x) dx \approx (b - a) \left\lbrack y_{0}\frac{\int_{0}^{1}{\left( t - \frac{1}{n} \right) \left( t - \frac{2}{n} \right) \ldots\ (t - 1) dt}}{\left( 0 - \frac{1}{n} \right) \left( 0 - \frac{2}{n} \right) \ldots\ (0 - 1) } + y_{1}\frac{\int_{0}^{1}{(t - 0) \left( t - \frac{2}{n} \right) \ldots\ (t - 1) dt}}{\left( \frac{1}{n} - 0 \right) \left( \frac{1}{n} - \frac{2}{n} \right) \ldots\ \left( \frac{1}{n} - 1 \right) } + \ldots + y_{n}\frac{\int_{0}^{1}{(t - 0) \left( t - \frac{1}{n} \right) \ldots\ \left( t - \frac{n - 1}{n} \right) }}{(1 - 0) \left( 1 - \frac{1}{n} \right) \ldots\ \left( 1 - \frac{n - 1}{n} \right) } \right\rbrack = (b - a) \left\lbrack c_{n^{0}}y_{0} + c_{n^{1}}y_{1} + \ldots + c_{n^{n}}y_{n} \right\rbrack, }$

мұнда

$C_{n^{i}}\frac{\int_{0}^{1}{(t - 0) \left( t - \frac{1}{n} \right) \ldots\ \left( t - \frac{i + 1}{n} \right) \ldots(t - 1) dt}}{\left( \frac{i}{n} - 0 \right) \left( \frac{i}{n} - \frac{1}{n} \right) \ldots\ \left( \frac{i}{n} - \frac{i + 1}{n} \right) \ldots\left( \frac{i}{n} - 1 \right) }$ .