Математикалық талдаудың тура және кері есептері


Жұмыс түрі: Дипломдық жұмыс
Тегін: Антиплагиат
Көлемі: 82 бет
Таңдаулыға:
ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ
ҒЫЛЫМ МИНИСТРЛІГІ
А. Ясауи атындағы Халықаралық қазақ-түрік университеті
Қорғауға жіберілді
Д И П Л О М Д Ы Қ Ж Ұ М Ы С
НАБИШЕВ ДИЛМУРАТ МУХАМАТСАЛИЕВИЧ
Жаратылыстану факультетінің 4-курс
ЖМА-912 тобының студенті
ТАҚЫРЫБЫ: МАТЕМАТИКАЛЫҚ ТАЛДАУДЫҢ ТУРА ЖӘНЕ КЕРІ ЕСЕПТЕРІ
Ғылыми жетекшісі:
ф. -м. ғ. д. Турметов Б. Х.
Түркістан - 2013 жыл
Қазақстан Республикасы Білім және ғылым министрлігі
А. Ясауи атындағы халықаралық қазақ-түрік университеті
Математика кафедрасы
«Қорғауға жіберілді»
Кафедра меңгерушісі
профессор Ә. С. Мұратов
ДИПЛОМДЫҚ ЖҰМЫС
Тақырыбы: Математикалық талдаудың тура және кері есептері
5В060100 - « Математика» мамандығы бойынша
Орындаған Набишев Д. М.
Ғылыми жетекшісі
ф. м. ғ. д., аға оқытушы Турметов Б. Х.
Түркістан 2013
Мазмұны
Математикалық талдаудың кейбір күрделі қасиеттерге
ие болған функцияларын құру . . .
Кіріспе
Зерттеу тақырыбынының көкейтестілігі. Математика саласында жазылатын мақалалар және монографияларда, студенттерге математикалық пәндер бойынша оқытылатын лекцияларда және өқулықтарда теориялық материалдарды толық түсінтіру үшін әдетте көптеген тура және кері мысалдар көрсетіледі [1-7] .
Олардың ішінде кері мысалдарды зерттеу өте маңызды болып табылады. Себебі мұндай мысалдар арқылы теориялық курстарда дәлелденген теоремалардың кейбір шарттары орындалмаған жағдайды зерттеу арқылы берілген шарттардың маңызыдлығын толығынан түсінуге болады. Математикалық талдау курсында оқытылатын тақырыптарға сәйкес кері мысалдар құру өте күрделі мәселе. Сол себептен бұл дипломдық жұмыста осы тақырпқа тиісті проблемалар қарастырылады.
Дипломдық жұмыста негізгі мақсаты бір және көп аргументке тәуелді функциялар теориясының кері мысалдарын қарастыру. Математикалық талдаудың осы тақырыптарға тиісті негізгі теоремаларын талдау жасау, берілген шарттары орындалмаған жағдайларға сәйкес кері мысалдар құру болып табылады.
Сондай-ақ жұмыста қарапайым қасиеттерге ие болған кұрделі функцияларды құру мысалдарыда келтіріледі.
Дипломдық жұмстың құрылымы :
Жұмыс Кіріспе, 9 параграфқа бөлінген 3 тарау, қорытынды және пайдаланылған әдебиеттер тізімінен турады.
Бірінші тарауда бір аргументке тәуелді функциялардың қасиеттеріне байланысты кері мысалдар келтіріледі. Мұнда функция қасиеттері туралы кері теоремалар, функцияның шегі және үзілісіздігі, функцияның туындысы және интегралдау теориясымен байланысты кері есептері сияқты тақырыптар қамтылған.
Екінші тарауда көп аргументке тәуелді функцияларды зерттеуге арналған кері мысалдар қарастырылады. Мұнда көп айнымалы функциялар, олардың шегі, үзіліссіздігі көп айнымалы функциялардың дифференциалдық есептеуі, еселі және қисық сызықты интегралдар туралы кері есептер сияқты тақырыптарға сәйкес келетін мысалдар көрсетілген.
Үшінші тарауда кұрделі функцияларды құру мысалдары көрсетілген.
1 Бір аргументке тәуелді функциялар теориясының кері теоремалары
1. 1 Функция қасиеттері туралы кері теоремалар
1. Әрі жұп, әрі тақ болған функция.
Функцияның зерттеу барысында біз оның жұп, тақ немесе жұпта емес тақта емес болатынын білеміз. Бірақ, бір уақытта жұпта, тақта болатын функция да бар болатынын көрсетейік.
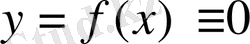 функциясы үшін
функциясы үшін
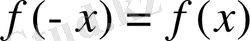 ,
,
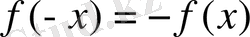 ,
,

теңсіздіктері орындалатыны белгілі. Демек
,
 функция әрі жұп, әрі тақ болады. Мұндай қасиеттке ие болған басқа функция жоқ. Шындығында да, егер симметриялы
Е
жиынында берілген
функция әрі жұп, әрі тақ болады. Мұндай қасиеттке ие болған басқа функция жоқ. Шындығында да, егер симметриялы
Е
жиынында берілген
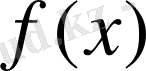 үшін
үшін
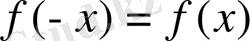 Equation. 3,
Equation. 3,
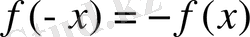 Equation. 3,
Equation. 3,
 Equation. 3
Equation. 3
болса, онда
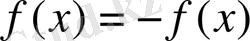 Equation. 3,
немесе
Equation. 3,
немесе
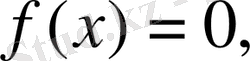 Equation. 3
Equation. 3
 Equation. 3
Equation. 3
болады.
2. Монотонды функциялардың қосындысы монотонды функция болмаған жағдайға мысал .
Егер
 функциялары бір уақытта монотон өспелі немесе монотон кемімелі болса, олардың қосындысы да монотонды болама деген сұраққа жауап берейік.
функциялары бір уақытта монотон өспелі немесе монотон кемімелі болса, олардың қосындысы да монотонды болама деген сұраққа жауап берейік.
Айталық,
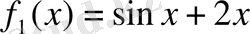 ,
,
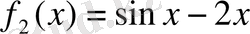 ,
,
 ,
,
болсын. Алдымен
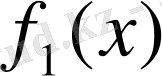 функциясының монотонды екендігін көрсетейік. Барлық
функциясының монотонды екендігін көрсетейік. Барлық
 үшін
үшін
 теңсіздігі орынды (бұл теңсіздіктің орынды болатынын функциялардың графиктарынан байқаса болады) .
теңсіздігі орынды (бұл теңсіздіктің орынды болатынын функциялардың графиктарынан байқаса болады) .
Олай болса, кез келген
 нүктелері үшін
нүктелері үшін

қатынастың орынды болатынын байқаймыз. Соңғы теңсіздіктен
немесе

Сонда, кез келген
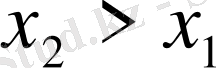 нүктелері үшін
нүктелері үшін
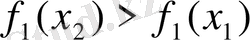 болатынын көреміз.
болатынын көреміз.
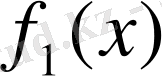 өспелі функция. Осыған ұқсас
өспелі функция. Осыған ұқсас
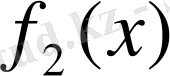 функциясыныңда монотонды (кемімелі) екендігін көрсету мүмкін. Бірақ олардың қосындысы
функциясыныңда монотонды (кемімелі) екендігін көрсету мүмкін. Бірақ олардың қосындысы
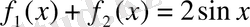 функциясы монотондылық қасиетке ие емес.
функциясы монотондылық қасиетке ие емес.
3. Ең кіші оң периоды болмайтын периодты функция.
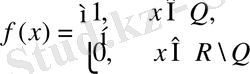 Equation. 3
Equation. 3
Дирихле функциясын қарастырайық. Кез-келген рационал сан бұл функцияның периоды болады. Шынында да,
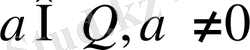 Equation. 3 болса,
Equation. 3 болса,
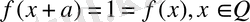 Equation. 3
Equation. 3
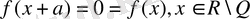 Equation. 3
Equation. 3
тепе-теңдіктер орынды болады. Демек, барлық
 , үшін
, үшін
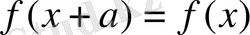 , теңдігі орындалады және
, теңдігі орындалады және
 саны Дирихле функциясының периоды болады. Сондықтан бұл функция периодты, бірақ ең кіші оң периоды жоқ.
саны Дирихле функциясының периоды болады. Сондықтан бұл функция периодты, бірақ ең кіші оң периоды жоқ.
4. Периодты функциялардың қосындысы периодтты функция болмайтын жағдайға мысал.
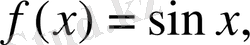 Equation. 3
Equation. 3
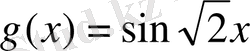 Equation. 3
Equation. 3
болсын.
 Equation. 3 функциясының периоды
Equation. 3 функциясының периоды
 Equation. 3,
Equation. 3,
 Equation. 3 функциясының периоды
Equation. 3 функциясының периоды
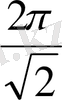 Equation. 3 тең.
Equation. 3 тең.
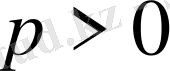 саны
саны
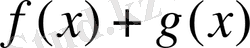 функциясының периоды деп есептейік. Бұл жағдайда барлық
функциясының периоды деп есептейік. Бұл жағдайда барлық
 үшін төмендегі теңдіктер орындалады:
үшін төмендегі теңдіктер орындалады:
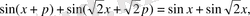
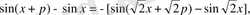
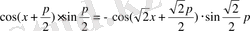
Егер
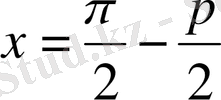 деп алсақ, соңғы теңдіктің сол жағы 0 ге тең және осыдан
деп алсақ, соңғы теңдіктің сол жағы 0 ге тең және осыдан
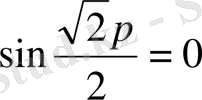 болады.
болады.
Демек,
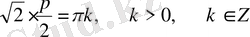 . (1)
. (1)
Енді
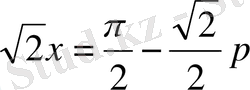 деп алсақ, яғни
деп алсақ, яғни
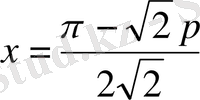 болса, теңдіктің оң жағы 0 ге тең және
болса, теңдіктің оң жағы 0 ге тең және
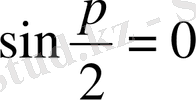 болады. Осыдан
болады. Осыдан
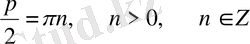 (2)
(2)
(1) және (2) теңдіктерге сәйкес
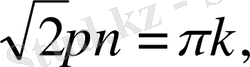
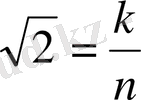 болады. Бірақ,
болады. Бірақ,
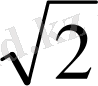 иррационал сан. Сол себептен
иррационал сан. Сол себептен
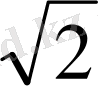 санын
санын
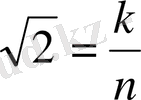 түрінде жазуға болмайды. Демек,
түрінде жазуға болмайды. Демек,
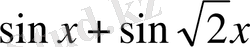 функциясы периодты болмайды.
функциясы периодты болмайды.
5. Анықталу облысының барлық нүктелері маңайында шектелмеген функция.
Төмендегі функцияны қарастырамыз.

Кез келген
 нүктені аламыз. Егер
нүктені аламыз. Егер
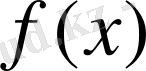 функциясы қандайда бір
функциясы қандайда бір
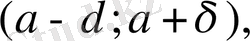
 аралықта шенелген болсаа, онда осы аралықта барлық
аралықта шенелген болсаа, онда осы аралықта барлық
 түріндегі бөлшектердің
түріндегі бөлшектердің
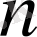 бөлімдері шектелген және осыдан бөлшектердің
бөлімдері шектелген және осыдан бөлшектердің
 алымдарыда шенелгендігі шығады. Нәтижеде
алымдарыда шенелгендігі шығады. Нәтижеде
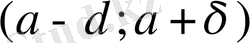 аралығында рационал болған
аралығында рационал болған
 бөлшектердің саны шектеулі болады. Мұндай қорытынды рационал сандар жиынының кез-келген аралықта тығыз болуы қасиетіне қайшы.
бөлшектердің саны шектеулі болады. Мұндай қорытынды рационал сандар жиынының кез-келген аралықта тығыз болуы қасиетіне қайшы.
1. 2 Функцияның шегі және үзілісіздігі
1. Шексіз және шенелген болып, шегі жоқ тізбектер.
Төмендегі тізбекті қарастырамыз:
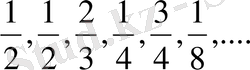
Мұнда тақ орындарда орналасқан элементтер
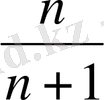 ,
,
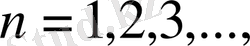 жұп орындарда орналасқан элементтер
жұп орындарда орналасқан элементтер
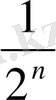 ,
,
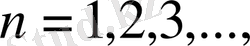 формулалар арқылы өрнектелген. Көріп тұрғанымыздай, мұндай тізбек шенелмеген және шегі жоқ екені анық. Сонымен бірге 0 және 1 сандары оның дербес шектері болады.
формулалар арқылы өрнектелген. Көріп тұрғанымыздай, мұндай тізбек шенелмеген және шегі жоқ екені анық. Сонымен бірге 0 және 1 сандары оның дербес шектері болады.
2. Бірі біріне орналасқан сегменттер тізбегі туралы.
Мынадай
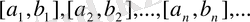 сегменттер тізбегі берілген болсын.
сегменттер тізбегі берілген болсын.
Егер


қатынастар орынды және
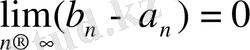
болса, онда мұндай тізбектер бірі біріне орналасқан сегменттер тізбегі деп аталады.
Бірі біріне орналасқан сегменттер теоремасы бойынша сегменттердің бір ғана ортақ нүктесі болады. Жоғарыда енгізілген шек әрқашан бар болады себебі
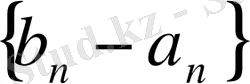 тізбегі кемімелі және төменнен 0 -мен шенелген.
тізбегі кемімелі және төменнен 0 -мен шенелген.
Егер
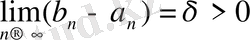
деп жорысақ, онда сегменттердің қиылысуының ұзындығы
 -ға тең сегмент болады.
-ға тең сегмент болады.
Егер сегменттердің орнына бірі біріне орналасқан интервалдарды алсақ, жоғарыдағы теорема орынды болмайды. Шынында да,
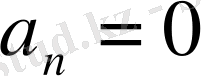 ,
,
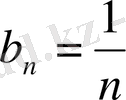 ,
,
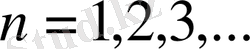
болсын. Бұл жағдайда
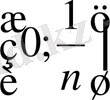 интервалдардыдың қиылысуы бос жиыннан тұрады.
интервалдардыдың қиылысуы бос жиыннан тұрады.
3. Шенелмеген болып, шексіз үлкен болмаған тізбек.
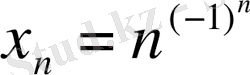 ,
,
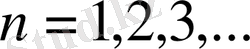
тізбегі үшін
 ,
,
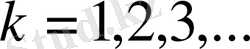 болғанда
болғанда
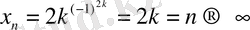 , егер
, егер
 . Демек, берілген тізбек шенелмеген болады. Бұл тізбек шексіз үлкен болуы үшін
. Демек, берілген тізбек шенелмеген болады. Бұл тізбек шексіз үлкен болуы үшін
 да
да
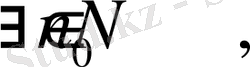
 -дер үшін
-дер үшін
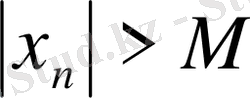 теңсіздігі орынды болуы керек екені белгілі. Бірақ,
теңсіздігі орынды болуы керек екені белгілі. Бірақ,
 ,
,
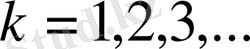 тақ сандар үшін
тақ сандар үшін
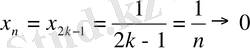 егер
егер
 .
.
Демек, берілген тізбек шексіз үлкен емес.
4. Анықталу облысының кез-келген нүктесінде шегі болмайтын функция.
Жоғарыда қарастырылған
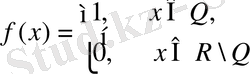 Equation. 3
Equation. 3
Дирихле функциясын аламыз. Кез-келген
 нүктесі
нүктесі
 жиынының да,
жиынының да,
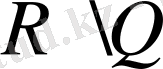 жиынының да шек нүктесі болады және
жиынының да шек нүктесі болады және
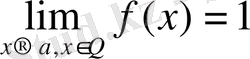 ,
,
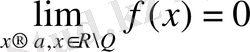
Демек, Дирихле функциясы шегінің жалғыздығы туралы қасиетке сүйеніп ешбір нүктеде шекке ие емес.
5. Салыстыру мүмкін болмаған шексіз аз функциялар
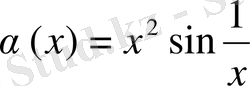 ,
,
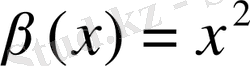 ,
,
 да шексіз аз болады, яғни
да шексіз аз болады, яғни
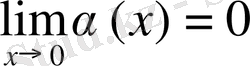 ,
,
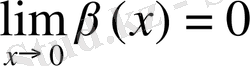
Олардың 0 -ге ұмтылу жылдамдықтарын салыстырамыз,
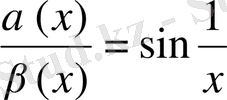
болады.
 да
да
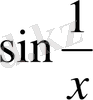 функциясының шегі жоқ, себебі
функциясының шегі жоқ, себебі
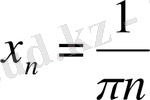
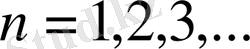 үшін
үшін
 да
да
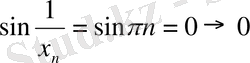 ,
,
 , бірақ
, бірақ
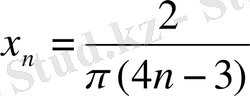 ,
,
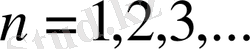 үшін
үшін

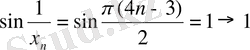 ,
,
 . Демек,
. Демек,
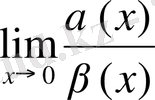 шек болмайды, яғни
шек болмайды, яғни
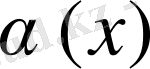 және
және
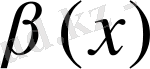 функцияларын салыстыру мүмкін емес.
функцияларын салыстыру мүмкін емес.
6. Анықталу облысының барлық нүктелерінде үзіліске ие болған функция.
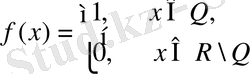 Equation. 3
Equation. 3
Дирихле функциясы кез келген нүктеде үзіліске ие болады.
7. Анықталу облысының бір ғана нүктесінде үзіліссіз болған функция.
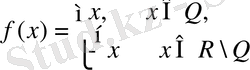
болсын. Егер
 болса, онда
болса, онда
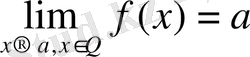
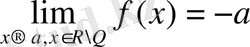
Демек, кез-келген
 нүктеде функция үзіліске ие болады.
нүктеде функция үзіліске ие болады.
Егер
 болса,
болса,
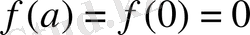 және
және

 ,
,
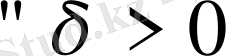 ,
,
 теңсіздігінен
теңсіздігінен
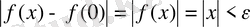
келіп шығады. Мұнда
 деп алсақ жеткілікті. Демек,
деп алсақ жеткілікті. Демек,
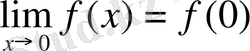 , яғни
, яғни
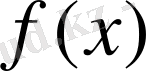 функция
функция
 нүктесінде үзіліссіз.
нүктесінде үзіліссіз.
8.
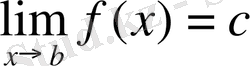 ,
,
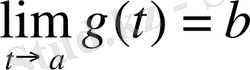 ,
,
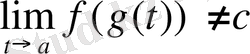 қатынастарды қанағаттандыратын үзіліссіз күрделі функция.
қатынастарды қанағаттандыратын үзіліссіз күрделі функция.
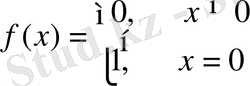
 ,
,
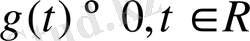
болсын. Бұл жағдайда
 үзіліссіз функция болады.
үзіліссіз функция болады.
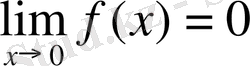 ,
,
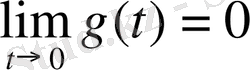 екені белгілі, бірақ
екені белгілі, бірақ
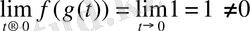
Келтірілген кері мысалдың бар болуы
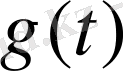 функция үшін
функция үшін
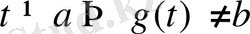
шартының жетіспегендігінен келіп шығады. Екінші жағынан, күрделі функцияның үзіліссіздігі туралы теореманы ескерсек, берілген қатыстарда
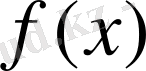 функцияның
функцияның
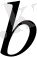 нүктедегі, яғни мысалды алсақ
нүктедегі, яғни мысалды алсақ
 дегі үзіліссіздік шарты жетіспейді.
дегі үзіліссіздік шарты жетіспейді.
9. К. Вейерштрасс теоремасы туралы.
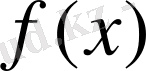 функциясы
функциясы
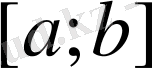 кесіндіде үзіліссізболса, ол осы кесіндіде шенелген және өзінің ең жоғары және ең төменгі шегіне жететіндігі белгілі.
кесіндіде үзіліссізболса, ол осы кесіндіде шенелген және өзінің ең жоғары және ең төменгі шегіне жететіндігі белгілі.
Теоремадағы
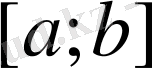 кесінді және
кесінді және
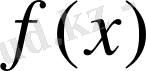 функциясының үзіліксіздігі маңызға ие. Сондай-ақ,
функциясының үзіліксіздігі маңызға ие. Сондай-ақ,
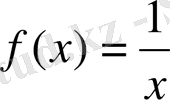 функция
функция
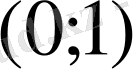 да үзіліссіз, бірақ шенелмеген болады. Сонымен қатар,
да үзіліссіз, бірақ шенелмеген болады. Сонымен қатар,
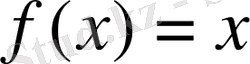 функция
функция
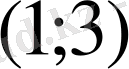 да үзіліссіз болып,
да үзіліссіз болып,
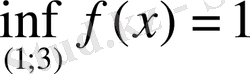 ,
,
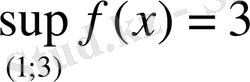
мәндерін
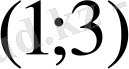 да қабылдай алмайды. Төмендегі
да қабылдай алмайды. Төмендегі
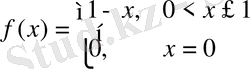
функциясы
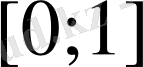 кесіндіде берілген болып,
кесіндіде берілген болып,
 да үзіліске ие
да үзіліске ие
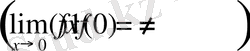
Бұл функция
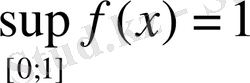
мәнін
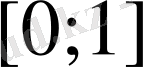 Equation. 3 да қабылдай алмайды.
Equation. 3 да қабылдай алмайды.
10. Больцано-Коши теоремасы туралы.
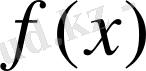 функциясы
функциясы
 кесіндіде үзіліссіз болып,
кесіндіде үзіліссіз болып,
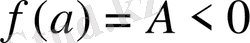 ,
,
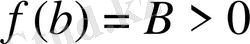 болса, онда
болса, онда
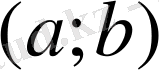 да ең болмағанда бір
да ең болмағанда бір
 нүктесі табылып,
нүктесі табылып,
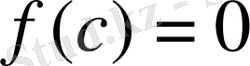 болады және
болады және
 қанағаттандыратын
қанағаттандыратын
 үшін
үшін
 табылып,
табылып,
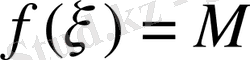 болатындығы белгілі.
болатындығы белгілі.
Егер
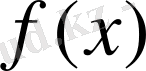 функциясы үзіліссіз болмаса, теореманың қортындысы дұрыс емес болуы мүмкін. Мысалы,
функциясы үзіліссіз болмаса, теореманың қортындысы дұрыс емес болуы мүмкін. Мысалы,
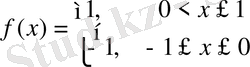
функция
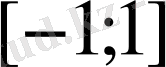 кесіндіде берілген болып,
кесіндіде берілген болып,
 де үзіліске ие.
де үзіліске ие.
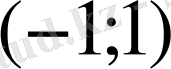 аралығында
аралығында
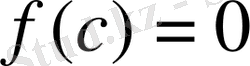 теңдігін қанағаттандыратын
теңдігін қанағаттандыратын
 нүктесі де
нүктесі де
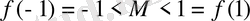 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
 үшін қайсыбір
үшін қайсыбір
 (
(
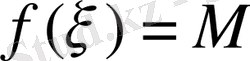 болатын) нүкте жоқ екендігі айқын.
болатын) нүкте жоқ екендігі айқын.
11. Бірқалыпты үзіліссіз функциялардың көбейтіндісі бірқалыпты үзіліссіз функция болмайтын жағдайға мысал.
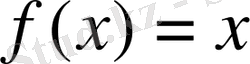 ,
,
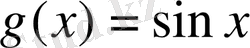 ,
,

болсын.
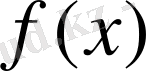 функция бірқалыпты үзіліссіз болуы белгілі.
функция бірқалыпты үзіліссіз болуы белгілі.
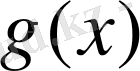 функциясы үшін
функциясы үшін
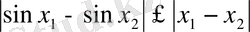 ,
,
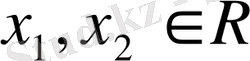 қатынасы орынды. Осыдан
қатынасы орынды. Осыдан
 деп алсақ, онда
деп алсақ, онда
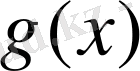 функциясы да бірқалыпты үзіліссіз болады. Функциялардың көбейтіндісі үшін төмендегі екі тізбекті аламыз:
функциясы да бірқалыпты үзіліссіз болады. Функциялардың көбейтіндісі үшін төмендегі екі тізбекті аламыз:
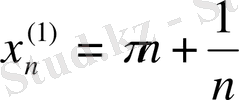 ,
,
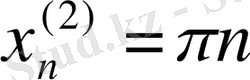 ,
,
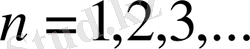 ,
,
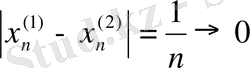 ,
,

екені белгілі, бірақ
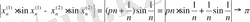 ,
,

Демек,
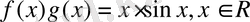 бірқалыпты үзіліссіз функция емес.
бірқалыпты үзіліссіз функция емес.
Функциялардың анықталу аймағы және
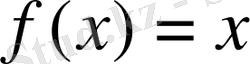 функция шенелмегендігі мұндай кері мысалдың шығуының себебі болады. Бірқалыпты үзіліссіз функция лар қосындысы әрқашанда бірқалыпты үзіліссіз функция болатынын айтып өту керек.
функция шенелмегендігі мұндай кері мысалдың шығуының себебі болады. Бірқалыпты үзіліссіз функция лар қосындысы әрқашанда бірқалыпты үзіліссіз функция болатынын айтып өту керек.
12. Кантор теоремасы туралы.
 кесіндіде үзіліссіз болған функция бірқалыпты үзіліссіз болатыны белгілі. Егер кесіндінің орнына
кесіндіде үзіліссіз болған функция бірқалыпты үзіліссіз болатыны белгілі. Егер кесіндінің орнына
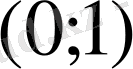 интервалын алсақ, теореманың қортындысы дұрыс емес болуы мүмкін. Мысалы,
интервалын алсақ, теореманың қортындысы дұрыс емес болуы мүмкін. Мысалы,
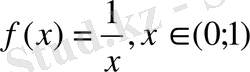
болсын.
 функция
функция
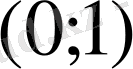 да үзіліссіз. Ол бірқалыпты үзіліссіз болсын деп ойлайық, яғни
да үзіліссіз. Ол бірқалыпты үзіліссіз болсын деп ойлайық, яғни
 , (
, (
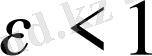 ),
),
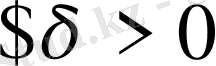 ,
,
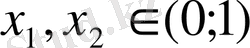
және
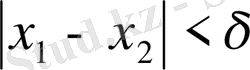 дан
дан
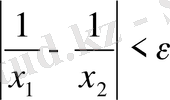 болады. Біз
болады. Біз
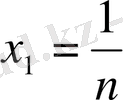 ,
,
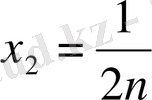 ,
,
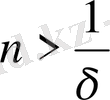 деп алуымыз мүмкін, себебі
деп алуымыз мүмкін, себебі
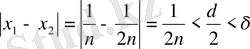
Бұл жағдайда
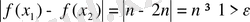 болады. Бұл теңсіздік ойлағанымызға қайшы, сондықтан
болады. Бұл теңсіздік ойлағанымызға қайшы, сондықтан
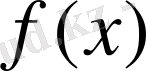 функция бірқалыпты үзіліссіз болмайды.
функция бірқалыпты үзіліссіз болмайды.
1. 3. Функцияның туындысы
1. Функцияның үзіліссіз болуы үшін туындының бар болуының қажет еместігі.
Функцияның үзіліссіз болуы үшін туындының бар болуы тек жеткілікті шарт болып, функция бірер нүктеде үзіліссіз болса, ол осы нүктеде туындыға ие болмауы да мүмкін. Мысалы,
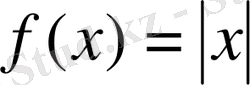 ,
,
 функция
функция
 нүктеде үзіліссіз, бірақ
нүктеде үзіліссіз, бірақ
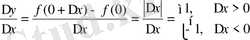 ,
,
яғни
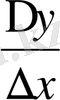 қатынасының
қатынасының
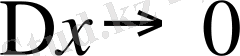 ғы шегі жоқ. Демек,
ғы шегі жоқ. Демек,
 да функцияның туындысы жоқ.
да функцияның туындысы жоқ.
2. Үзіліссіз және дифференциалданатын болып, туындысы үзілісті болған функция.
Мына
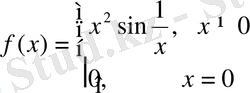
функцияны қарастырайық.
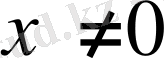 нүктелерде
нүктелерде
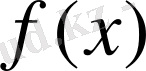 функцияның туындысы бар екендігі белгілі:
функцияның туындысы бар екендігі белгілі:
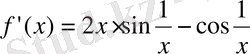 ,
,
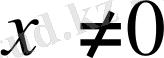
 нүктесінде
нүктесінде
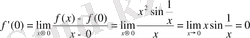
Демек,
 функция барлық нүктелерде туындыға ие және оның туындысы
функция барлық нүктелерде туындыға ие және оның туындысы
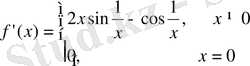
 функция
функция
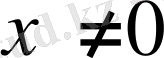 нүктелерде үзіліссіз болады, ал
нүктелерде үзіліссіз болады, ал
 нүктесінде үзіліске ие. Шынында да,
нүктесінде үзіліске ие. Шынында да,
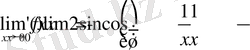
шек жоқ. Себебі
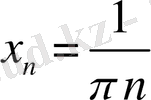 нүктелерін таңдап алсақ, онда
нүктелерін таңдап алсақ, онда
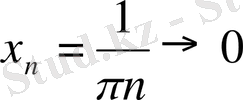 ,
,
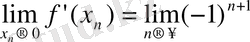
Соңғы тізбектің шегі болмайды.
3. Туындысы жұп функция болған жұпта емес және тақта емес функция.
Әдетте функция жұп немесе тақ болса, оның туындысы керісінше тақ немесе жұп болады . Ал жұпта емес, тақта емес функция берілсе жағдай қандай болады деген сұрақ туындайды.
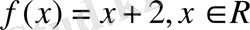 функциясы жұпта немесе тақта емес. Ал оның туындысы
функциясы жұпта немесе тақта емес. Ал оның туындысы
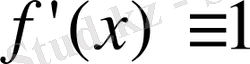 жұп функция болады.
жұп функция болады.
4.
 нүктеде туындысы шексіз болған үзіліссіз функция.
нүктеде туындысы шексіз болған үзіліссіз функция.
1 мысалға байланысты
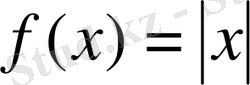 функция
функция
 нүктесінде үзіліссіз, бірақ туындысы болмайды. Енді
нүктесінде үзіліссіз, бірақ туындысы болмайды. Енді
 де үзіліссіз және туындысы шексіз болған функцияға мысал келтіреміз.
де үзіліссіз және туындысы шексіз болған функцияға мысал келтіреміз.
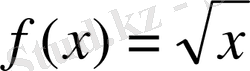 ,
,

болсын.
 нүктесінде
нүктесінде
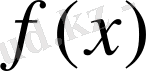 функция үзіліссіз болады (оң жағынан) . Сонымен бірге
функция үзіліссіз болады (оң жағынан) . Сонымен бірге
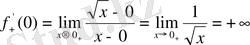
яғни
 нүктесінде функцияның туындысы (оң жағынан) бар және шексіз болады.
нүктесінде функцияның туындысы (оң жағынан) бар және шексіз болады.
Дифференциалдық есептеудің негізгі теоремалары және қолданылуы
Дифференциалдық есептеудің негізгі теоремаларын келтірейік .
Теорема (
Ферма)
.
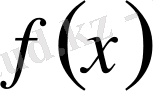 функциясы
функциясы
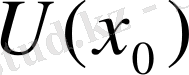 - де анықталып және осы маңайда өзінің ең үлкен және ең кіші мәндерін қабылдасын. Егер
- де анықталып және осы маңайда өзінің ең үлкен және ең кіші мәндерін қабылдасын. Егер
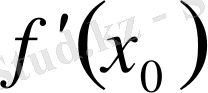 бар болса, онда
бар болса, онда
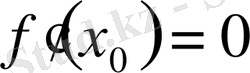 теңдігі орындалады.
теңдігі орындалады.
Теорема (
Ролль)
.
 функциясы
функциясы
1.
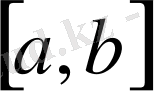 сегментінде үзіліссіз;
сегментінде үзіліссіз;
2.
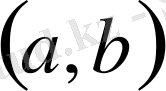 интервалында дифференциалдансын;
интервалында дифференциалдансын;
3.
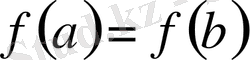 болсын, онда
болсын, онда
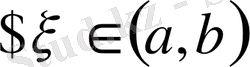 :
:

теңдігі орындалады.
Теорема (
Лагранж
) .
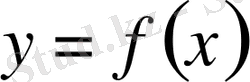 функциясы
функциясы
1.
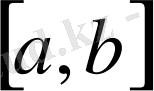 сегментінде үзіліссіз;
сегментінде үзіліссіз;
2.
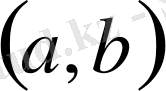 интервалында дифференциалдансын, онда
интервалында дифференциалдансын, онда
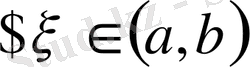 :
:
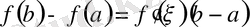
теңдігі орындалады.
Теорема (
Коши
) .
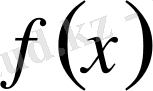 және
және
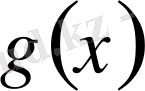 функциялары
функциялары
1.
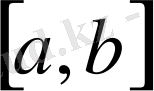 сегментінде үзіліссіз;
сегментінде үзіліссіз;
2.
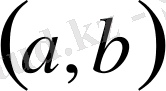 интервалында дифференциалдансын;
интервалында дифференциалдансын;
3.
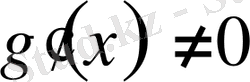 ,
,
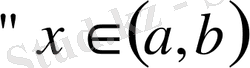 болса, онда
болса, онда
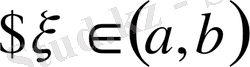 :
:
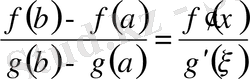
теңдігі орындалады.
5. Ферма теоремасы жайында.
Егер
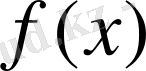 функция
функция
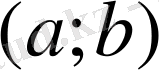 аралығында анықталған және қайсыбір ішкі
аралығында анықталған және қайсыбір ішкі
 нүктесінде ең үлкен (ең кіші) мәнге ие болса және осы нүктеде ақырлы
нүктесінде ең үлкен (ең кіші) мәнге ие болса және осы нүктеде ақырлы
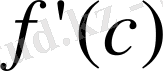 туындысы бар болса, онда
туындысы бар болса, онда
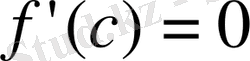 болады. Бұл нәтиже Ферма теоремасынан келіп шығады.
болады. Бұл нәтиже Ферма теоремасынан келіп шығады.
Кері теорема орынды емес, яғни
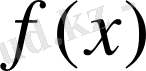 функциясының қайсыбір ішкі
функциясының қайсыбір ішкі
 нүктесіндегі туындысы
нүктесіндегі туындысы
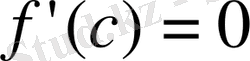 болсада, бұл нүктеде функция ең үлкен (ең кіші) мәніне ие болмауы мүмкін. Мысалы,
болсада, бұл нүктеде функция ең үлкен (ең кіші) мәніне ие болмауы мүмкін. Мысалы,
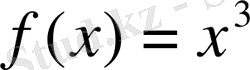 ,
,
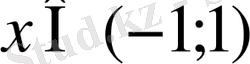 аралығында анықталған болсын. Бұл функция үшін,
аралығында анықталған болсын. Бұл функция үшін,
 нүктесінде
нүктесінде
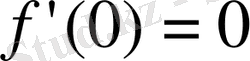 болады. Бірақ, функцияның бұл нүктедегі мәні
болады. Бірақ, функцияның бұл нүктедегі мәні
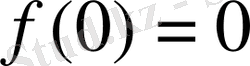 оның
оның
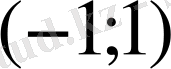 аралығындағы ең үлкен немесе ең кіші мәні болмайды.
аралығындағы ең үлкен немесе ең кіші мәні болмайды.
6. Ролл теоремасы жайында.
Егер
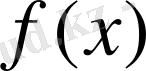 Equation. 3 функция
Equation. 3 функция
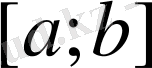 Equation. 3 кесіндіде берілген болып,
Equation. 3 кесіндіде берілген болып,
1)
аралығында үзіліссіз;
2)
аралығында дифференциалданатын;
3)
болса,
онда
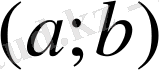 аралығында оның туындысы
аралығында оның туындысы
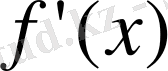 нолге тең болатын кем дегенде бір
нолге тең болатын кем дегенде бір
 нүкте табылады (яғни
нүкте табылады (яғни
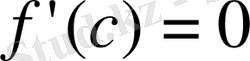 ,
,
 ) . Ролл теоремасындағы 1) - 3) шартардың біреуі орындалмаса, онда бұл функцияның туындысының мәні
) . Ролл теоремасындағы 1) - 3) шартардың біреуі орындалмаса, онда бұл функцияның туындысының мәні
 үшін нолге тең болмауы мүмкін. Бірақ, барлық шарттар орындалмаған жағдайда да
үшін нолге тең болмауы мүмкін. Бірақ, барлық шарттар орындалмаған жағдайда да
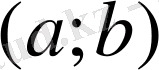 аралығында туынды 0 ге тең болатын нүктелер бар болуыда мүмкін, яғни теоремада берілген шарттар жеткілікті болып, қажетті емес.
аралығында туынды 0 ге тең болатын нүктелер бар болуыда мүмкін, яғни теоремада берілген шарттар жеткілікті болып, қажетті емес.
Мысалы,
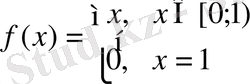
болсын. Бұл функция үшін Ролл теоремасында көрсетілген 2) және 3) -ші шарттар орындалып, 1) -ші шарт, яғни үзіліссіздік шарты орындалмайды. Сонымен бірге
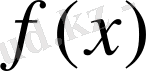 функциясының туындысы
функциясының туындысы
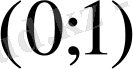 аралығында нолге тең емес;
аралығында нолге тең емес;
Келесі
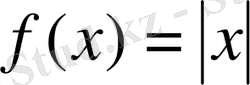 ,
,

функция үшін 2) -ші шарт орындалмайды (
 де туындысы жоқ) және
де туындысы жоқ) және
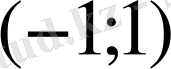 аралықта
аралықта
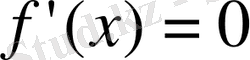 теңдігін қанағаттандыратын нүкте жоқ;
теңдігін қанағаттандыратын нүкте жоқ;
Егер
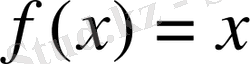 ,
,

болса, бұл функция үшін теореманың 3) -ші шарты орындалмайды (
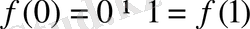 ) және
) және
 үшін
үшін
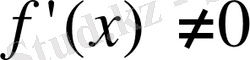 болады.
болады.
Келесі
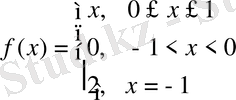
функция үшін Ролл теоремасының барлық шарттар орындалмайды, бірақ
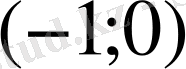 аралығының кез-келген нүктесінде
аралығының кез-келген нүктесінде
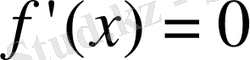 болады.
болады.
7. Лагранж теоремасы жайында.
Егер
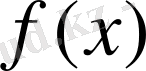 функция
функция
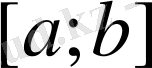 кесіндіде үзіліссіз және
кесіндіде үзіліссіз және
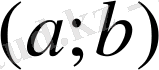 аралығында дифференциалданатын болса,
аралығында дифференциалданатын болса,
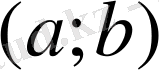 аралығында кем дегенде бір
аралығында кем дегенде бір
 нүкте табылып, төмендегі теңдік орынды болады:
нүкте табылып, төмендегі теңдік орынды болады:
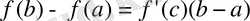 ,
,

Бұл нәтижені Лагранж теоремасы деп атайды.
Бұл теорема нақты мәнді функциялар үшін орынды. Шынында да
 функциясының мәндері комплекс сандар болсын деп есептейік.
функциясының мәндері комплекс сандар болсын деп есептейік.
Мысалы,
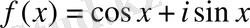 ,
,
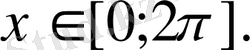
болсын.
Бұл жағдайда Лагранж теоремасының шарттары орындалып, қорытындысы дұрыс емес болады. Шынында да,
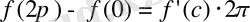
теңдігінен
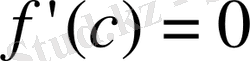 яғни
яғни
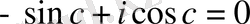 келіп шығады. Соңғы теңдік бір мезгілде
келіп шығады. Соңғы теңдік бір мезгілде
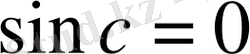 ,
,
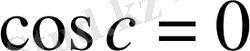 болғанда ғана орындалады. Ал бұл нәтиже негізгі тригонометриялық тепе теңдікке қайшы болған қорытынды.
болғанда ғана орындалады. Ал бұл нәтиже негізгі тригонометриялық тепе теңдікке қайшы болған қорытынды.
Лагранж теоремасындағы шарттардың біреуі орындалмаса, теореманың қорытындысы дұрыс болмауы мүмкін.
Мысалы,
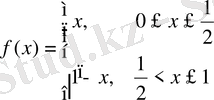
функция
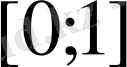 да үзіліссіз болып,
да үзіліссіз болып,
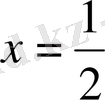 нүктеде туындысы болмайды.
нүктеде туындысы болмайды.
Сонымен бірге
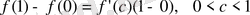
теңдік, яғни
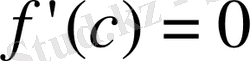 теңдік
теңдік
 үшін орындалмайды.
үшін орындалмайды.
8. Тейлор формуласы көмегімен e санының иррационалдығын дәлелдеу.
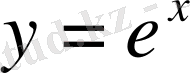 ,
,
 функциясы үшін Тейлор формуласы төмендегі көріністе жазылатындығы белгілі:
функциясы үшін Тейлор формуласы төмендегі көріністе жазылатындығы белгілі:
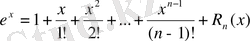
Мұндағы
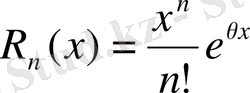 ,
,
 Лагранж формасындағы қалдық мүше деп аталады. Әдетте жоғарыдағы формуланы Маклорен формуласы деп те айтады.
Лагранж формасындағы қалдық мүше деп аталады. Әдетте жоғарыдағы формуланы Маклорен формуласы деп те айтады.
Егер
 болса, төмендегі теңдікке ие боламыз:
болса, төмендегі теңдікке ие боламыз:
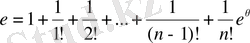 ,
,

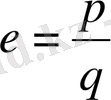 - рационал сан болсын деп есептейік.
- рационал сан болсын деп есептейік.
 болғандықтан
болғандықтан
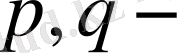 натурал және
натурал және
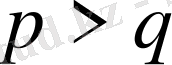 болады. Демек,
болады. Демек,
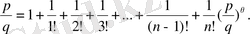 (*)
(*)
Теңдіктің екі жағын
 -ға көбейтсек төмендегі теңдікті аламыз:
-ға көбейтсек төмендегі теңдікті аламыз:
 . (**)
. (**)
Бұл жерде
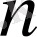 санын
санын
 дан үлкен деп алуымыз мүмкін. Бұл жағдайда
дан үлкен деп алуымыз мүмкін. Бұл жағдайда
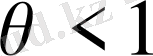 ,
,
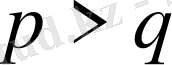 болғандықтан
болғандықтан
болады. Сондай-ақ,
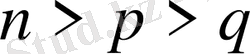 болғандықтан (*) теңдіктің сол жағы бүтін сан болады. (*) теңдіктің оң жағы (**) теңдікке сәйкес бірден кіші оң сан болады. Демек,
болғандықтан (*) теңдіктің сол жағы бүтін сан болады. (*) теңдіктің оң жағы (**) теңдікке сәйкес бірден кіші оң сан болады. Демек,
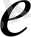 санын рационал сан деп есептегеніміз қайшылыққа алып келеді. Сондықтан,
санын рационал сан деп есептегеніміз қайшылыққа алып келеді. Сондықтан,
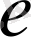 саны рационал сан болады.
саны рационал сан болады.
9. Лопитал ережесі жайында
Егер
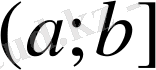 аралығында үзіліссіз
аралығында үзіліссіз
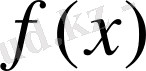 және
және
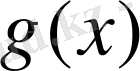 функциялары берілген болып,
функциялары берілген болып,
1)
Equation. 3 да
Equation. 3 және
Equation. 3 бар және
Equation. 3 ;
2)
Equation. 3
3)
бар болса,
онда
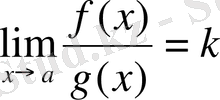
болады.
Лопитал ережесінде
 түрдегі анықталмағандық беріліп, жоғарыдағы
түрдегі анықталмағандық беріліп, жоғарыдағы
1) -3) шарттар орындалса, функциялар туындысының қатынасынан шек алынып, берілген функциялар қатынасының шегі табылады. Берілген функциялар қатынасының шегі 3) шарт орындалмаса да бар болуы мүмкін, яғни 3) шарт жеткілікті болып, қажетті емес.
Мысалы,
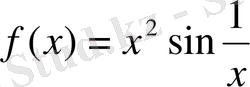 ,
,
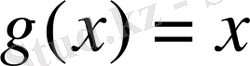
функциялар
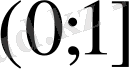 аралығында 1), 2) шарттарды қанағаттандырады және
аралығында 1), 2) шарттарды қанағаттандырады және
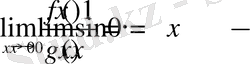
Бірақ,
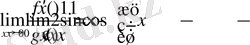
шек жоқ.
10. Туындысы қайсыбір нүктеде оң болып, бұл нүктенің маңайында монотонды болмаған дифференциалданатын функция.
Егер
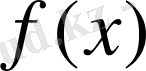 функциясы қандайда бір
функциясы қандайда бір
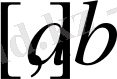 аралықта дифференциалданатын және монотонды өспелі (кемімелі) болса, онда
аралықта дифференциалданатын және монотонды өспелі (кемімелі) болса, онда
 болады.
болады.
Кері теорема орынды емес, яғни
 болса
болса
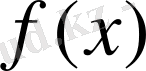 функциясы монотонды болуы шарт емес. Мысалы
функциясы монотонды болуы шарт емес. Мысалы
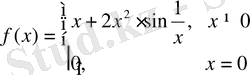
болсын.
 функциясы барлық нүктелерде туындыға ие және
функциясы барлық нүктелерде туындыға ие және
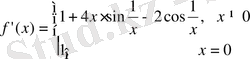
Демек,
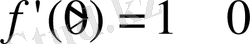 болады. Төмендегі
болады. Төмендегі
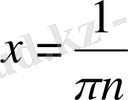 ,
,
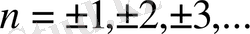
нүктелерде туындының мәндерін есептейміз:
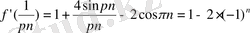 ,
,
Демек,
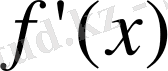 функциясы,
функциясы,
 нүктенің маңайында әрі оң, әрі теріс мәндерді қабылдайды. Осыдан
нүктенің маңайында әрі оң, әрі теріс мәндерді қабылдайды. Осыдан
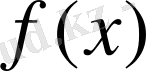 функциясының өзі
функциясының өзі
 -дің маңайында туындысы бар, бірақ монотон функция еместігі келіп шығады.
-дің маңайында туындысы бар, бірақ монотон функция еместігі келіп шығады.
11. Дифференциалданатын және шенелген болып, туындысы шенелмеген функция.
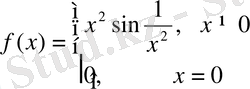
функциясы
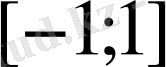 кесіндіде төмендегі шекті туындыға ие
кесіндіде төмендегі шекті туындыға ие
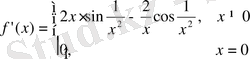
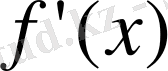 функциясы
функциясы
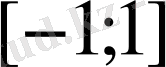 кесіндіде шенелмеген болады. Шынында да,
кесіндіде шенелмеген болады. Шынында да,
 нүктенің маңайында
нүктенің маңайында
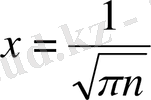 ,
,
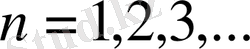 нүктелерде
нүктелерде

12. Күдікті нүктеде экстремумға ие болмаған функция.
Анықтама.
Егер
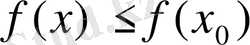 (
(
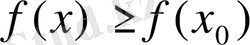 ),
),
 теңсіздігі орындалса, онда
теңсіздігі орындалса, онда
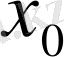
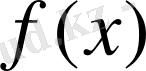 функциясының максимум (минимум) нүктесі деп аталады.
функциясының максимум (минимум) нүктесі деп аталады.
Функцияның максимум және минимум нүктелерін функцияның экстремумдары деп атайды.
Теорема. (экстремумның қажетті шарты) .
Егер
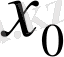 нүктесі
нүктесі
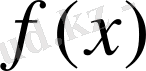 функциясының экстремум нүктесі болса, онда
функциясының экстремум нүктесі болса, онда
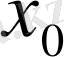 нүктесінде
нүктесінде
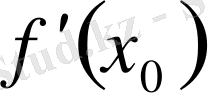 туындысы жоқ немесе
туындысы жоқ немесе
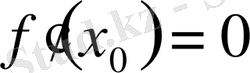 .
.
 болатын нүктелерді күдікті нүктелер деп атаймыз.
болатын нүктелерді күдікті нүктелер деп атаймыз.
Берілген функция күдікті нүктелерде максимал немесе минимал мәндеріне ие болу шарт емес.
Мысалы,
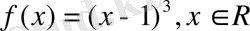
функция үшін
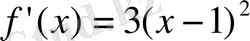 ,
,
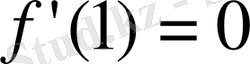 және
және
 күдікті нүкте болады. Бірақ,
күдікті нүкте болады. Бірақ,
 нүктенің қайсыбір маңайында
нүктенің қайсыбір маңайында
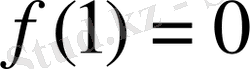 шама бұл функцияның ең кіші немесе ең үлкен мәні болмайды. Бұл нүктенің кез-келген маңайында функцияның нолден кіші және нолден үлкен мәндері қалауынша табылады.
шама бұл функцияның ең кіші немесе ең үлкен мәні болмайды. Бұл нүктенің кез-келген маңайында функцияның нолден кіші және нолден үлкен мәндері қалауынша табылады.
13. Экстремум нүктенің қайсыбір жағының маңайында туындысының таңбасы сақталмайтын дифференциалданатын функция.
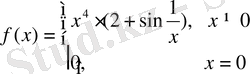
функция
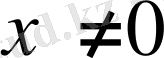 де оң мәндерді қабылдайды. Сондықтан
де оң мәндерді қабылдайды. Сондықтан
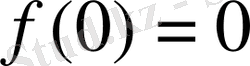 мәні оның экстремум(минимумы) болады. Бұл функцияның туындысы
мәні оның экстремум(минимумы) болады. Бұл функцияның туындысы
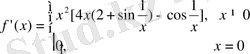
 нүктенің кез-келген маңайында әрі оң, әрі теріс мәндерді қабылдайды. Шынында да,
нүктенің кез-келген маңайында әрі оң, әрі теріс мәндерді қабылдайды. Шынында да,
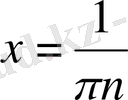 лар үшін
лар үшін
Демек,
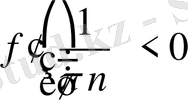 Equation. 3, егер
Equation. 3, егер
 Equation. 3,
Equation. 3,
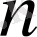 Equation. 3 - жұп сан.
Equation. 3 - жұп сан.
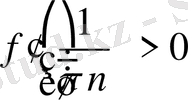 Equation. 3, егер
Equation. 3, егер
 Equation. 3,
Equation. 3,
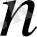 Equation. 3 -тақ сан
Equation. 3 -тақ сан
болса. Осыдан
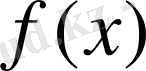 функция
функция
 -дің оң жақ маңайында монотонды бола алмайтындығынан келіп шығады. Осыған ұқсас
-дің оң жақ маңайында монотонды бола алмайтындығынан келіп шығады. Осыған ұқсас
 - дің сол жақ маңайында да
- дің сол жақ маңайында да
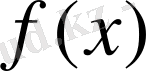 функциясының туындысының таңбасы сақталмайды және монотонды болмайды.
функциясының туындысының таңбасы сақталмайды және монотонды болмайды.
14. Күдікті нүктенің сол жағынан оң жағына өткенде туындысының таңбасы “ - ” тан “ +” ке өзгерседе бұл нүкте максимум нүктесі болатын функция.
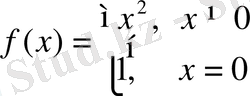
функция үшін
 Equation. 3 экстремум(максимум) нүктесі болады. Шынында да,
Equation. 3 экстремум(максимум) нүктесі болады. Шынында да,
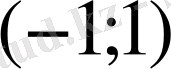 интервалының нүктелері үшін
интервалының нүктелері үшін
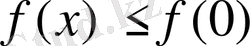 теңсіздігі орынды болады. Демек,
теңсіздігі орынды болады. Демек,
 максимум нүктесі болады. Сонымен қатар
максимум нүктесі болады. Сонымен қатар
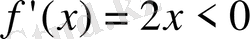 , егер
, егер
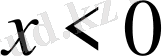
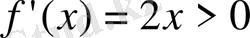 , егер
, егер

болса, яғни
 ден солдан оңға өткенде туындының таңбасы минустан плюске өзгереді.
ден солдан оңға өткенде туындының таңбасы минустан плюске өзгереді.
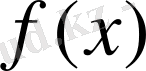 функция кризистік нүктеде үзіліссіз болса, туындысының таңбасы минустан плюске өзгергенінен осы нүкте
функция кризистік нүктеде үзіліссіз болса, туындысының таңбасы минустан плюске өзгергенінен осы нүкте
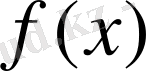 үшін минимум нүкте болатындығын атап өтуіміз керек.
үшін минимум нүкте болатындығын атап өтуіміз керек.
15. Экстремум нүктенің сол жағынан оң жағына өткенде туындысының таңбасы өзгермейтін функция.
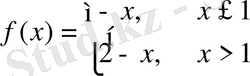
функция үшін
 экстремум (минимум) нүкте болады. Шынында да,
экстремум (минимум) нүкте болады. Шынында да,
 -нің
-нің
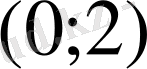 маңайындағы барлық нүктелер үшін
маңайындағы барлық нүктелер үшін
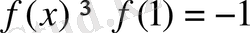
теңсіздігі орынды болады. Сонымен қатар
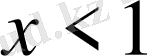 және
және
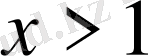 нүктелер үшін
нүктелер үшін
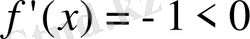 , яғни туынды таңбасын өзгертпейді. Осындай кері мысалдың пайда болуына
, яғни туынды таңбасын өзгертпейді. Осындай кері мысалдың пайда болуына
 функция
функция
 нүктеде үзіліссіз болмайтындығы себеп болады.
нүктеде үзіліссіз болмайтындығы себеп болады.
16. Қисық сызықтың иілу нүктесі туралы.
Анықтама.
 функциясы
функциясы
 интервалында анықталсын және
интервалында анықталсын және
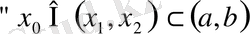 нүктесі үшін
нүктесі үшін
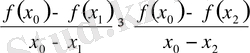
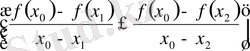
теңсіздігі орындалса,
 функциясы
функциясы
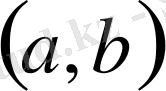 - да дөңес (ойыс) функция деп аталады.
- да дөңес (ойыс) функция деп аталады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz