Қатты денелер қирау табиғатын кинетикалық бағытта зерттеу

Кіріспе.
1.1. Беріктілік проблемаларды шешуде статикалық және кинетикалық көзқарастар.
1.2 Қатты денелердің жарамдылық мерзімі және беріктілік кинетикалық концепциясының негіздері.
1.3. Жарамдылық мерзімді анықтау тәсілі.
1.4 Күрделі жағдайда материалдардың жарамдылық мерзімін анықтау тәсілдері.
2.1.Жарамдылық мерзімнің жалпы теңдеуі және жылулық қозғалыстың механикалық қираудағы негізгі рөлі.
2.2. Жылулық флуктуация және қирау процесінде оның ролі.
2.3. Қатты денелерді қирататын элементар акт процестері жөнінде.
Қорытынды.

Денелердің беріктілігін зерттеу проблемасы қайтадан қаралу барысына негізделген. Қайтадан қараудың екі негізгі себебі бар:
-біріншіден, дене қирау мәселесін жаңа көзқараспен қарастырудың дамуы, қирау процесінде атом және молекулалардың жылулық козғалысын есепке алу, яғни қирауды кинетикалық процесс деп түсіну;
-екіншіден, әр түрлі физикалық және физика-химиялық әдістер атом-молекулалық деңгейде жүктелген денелерде өтетін құбылыстарды анықтауда кеңінен қолдана басталуы.
Әрине, беріктілік ғылымының дамуына материалдарға қойылатын талап пен қолдану мүмкіншіліктері тез өзгеруі, беріктілікті интенсивті түрде зерттеуге өзінің әсерін тигізеді және ғылыми нәтижелерді практикада қолдануды қажет етеді.
Осы айтылған мәселелерді ескере отырып, беріктілік физикасын ғылымның ары қарай даму саласына жатқызуға болады. Жиналған эксперименттік мәліметтерге сүйене отырып, дененің механикалық қирауын кинетикалық деуге негіз тудыратынын қарастырып, осы бағыттағы проблемаларды талдау, беріктіліктің кинетикалық концепциясының ары қарай дамуын және басқа проблемаларды қарастыру, осы арнайы курстың мақсатына жатады.

1. Я.И. Френкель, Кинетическая теория жидкостей, изд-во АН СССР, 1945.
2. Я.И. Френкель, Введение в теорию металлов, Физматгиз, 1958.
3. С.Н. Журков, Вестн. АН СССР, №11, 78 (1957).
4. С.Н. Журков, Изв. АН СССР, сер «Неорг.материалы» 3, 1767 (1967).
5. С.Н. Журков, Вестн. АН СССР, №3, 46 (1968).
6. С.Н. Журков, Т.П.Санфилова, Докл. АН СССР, №101, 237 (1955).
7. С.Н. Журков, Т.П.Санфилова, ЖТФ 28, 1721 (1958).
8. A.A. Griffith, Phil. Trans. Roy. Soc. 221A, 163 (1921).
9. А.Ф. Иоффе, М.В. Кирпичева, М.А. Левицкая, ЖРФХО, ч. Физич.56, 489. (1924).
10. А.Ф. Иоффе, Физика кристаллов, Росиздат, 1929.
11. E. Orawan, Nature 154,341 (1944).
12. J.B. Murgatroid, Nature 154, 51 (1944).
13. J.B. Murgatroid, R.F. Sykes, Nature 156, 716 (1945).

Пән: Физика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 38 бет
Таңдаулыға:

Ф-ОБ-001033
Жұмыстың мақсаты.
Академик С.Н.Журковтың материалдардың қирау кинетикалық концепциясында
әрбір материалдың құрылым сезімтал коэффициенті материялдың бастапқы күйіне
байланысты тұрақты болып, материялды өңдеу арқылы полимерлерге оларды
ориентациялау, пластификациялау т.б. металдарға және олардың қоспаларына
термикалық өңдеу т.б. арқылы өзгереді, ал әрбір материалдың қирау
активациялық энергиясы жоғарыда көрсетілген өңдеулер әсер етпейтіндігі
дәлелденген. Дегенмен, Журков теңдеуіндегі құрылым сезімтал коэффициенті
қирау температурасына, жарамдылық мерзімге тәуелді емес. Осы есептеу ең
болмағанда теориялық деңгейде дискуссиялық мәселе. Шынында да, біріншіден
жүктелген материалдың атомаралық байланыстың қирауына байланысты жүктелген
жүк қирамаған байланыстарға таралып кернеудің өсуі, екіншіден нақты денеде
жүктелген жүк атомаралық байланыстарға біртекті әсерін тигізбейтіндігі
белгілі, себебі кез келген денелерде әртүрлі ақаулар кездеседі, олай болса,
бұл екі фактор үлгінің жарамдылық мерзіміне әсерін тигізуі керек. Бұл
факторлардың қаншалықты жарамдылық мерзімге және Журковтың ұсынған
теңдеуіне әсерін тигізуін нақтылау осы жұмыстың негізгі мақсаты болып
есептеледі.

Кіріспе.
Денелердің беріктілігін зерттеу проблемасы қайтадан қаралу барысына
негізделген. Қайтадан қараудың екі негізгі себебі бар:
-біріншіден, дене қирау мәселесін жаңа көзқараспен қарастырудың дамуы,
қирау процесінде атом және молекулалардың жылулық козғалысын есепке алу,
яғни қирауды кинетикалық процесс деп түсіну;
-екіншіден, әр түрлі физикалық және физика-химиялық әдістер атом-
молекулалық деңгейде жүктелген денелерде өтетін құбылыстарды анықтауда
кеңінен қолдана басталуы.
Әрине, беріктілік ғылымының дамуына материалдарға қойылатын талап пен
қолдану мүмкіншіліктері тез өзгеруі, беріктілікті интенсивті түрде
зерттеуге өзінің әсерін тигізеді және ғылыми нәтижелерді практикада
қолдануды қажет етеді.
Осы айтылған мәселелерді ескере отырып, беріктілік физикасын ғылымның
ары қарай даму саласына жатқызуға болады. Жиналған эксперименттік
мәліметтерге сүйене отырып, дененің механикалық қирауын кинетикалық деуге
негіз тудыратынын қарастырып, осы бағыттағы проблемаларды талдау,
беріктіліктің кинетикалық концепциясының ары қарай дамуын және басқа
проблемаларды қарастыру, осы арнайы курстың мақсатына жатады.
Беріктілік қатты денелердің негізгі қасиеттерінің бірі болып
есептелетіндігі белгілі. Беріктілік сыртқы жүктелген механикалық жүкке
төзімділігін сипаттайтын шама.
Беріктілік физикасының дамуын бірнеше этапқа белуге болады. Бірінші,
негізгі даму этабына, денелерді серпінді не болмаса тұтқыр-серпінді
біртұтас орта деп қарастырудан, денелер атом-молекулалық жүйе деп
қарастыруға өтуі жатады. Қатты денелерді бір-бірімен белгілі күшпен
байланысқан атомдардан құралған деген көзқарас, денеге жүк жүктелген
кездегі құбылысты таза механикалық түрде қарастыру, яғни жүктелген жүк
денедегі барлық атомдар арасындағы байланысқа бөлініп, оларды кернейді.
Дененің тұрақтылығы, денеге әсер етуші механикалық күш шамасы мен атомдар
арасындағы байланыс күш шамасының қатынасына байланысты. Егер әсер етуші
күш, атомдар арасындағы байланыс күштен аз шамада болса, денеде тек
серпінді деформация ғана болады. Егер тең не болмаса көп болса дене қирайды
не болмаса қайтымсыз (пластиктивті) деформацияланады. Қатты дененің
механикалық күш әсеріне реакциясының шамасын анықтау мақсатында дененің
серпінді шегі, ағу шегі және беріктілік шегі деген шамалар енгізілген. Осы
шамалардың енгізілуі атомдар жүйесімен жүктелген сыртқы
күш арасындағы әсерлесу таза механикалық әсерлесудің айғағы деп
айтуға болады. Сол себепті атомдар жүйесінің жүктелуіне байланысты тепе-
теңсіздікке өтуі критикалық түрде өтуін көрсетеді.
Бірақ, көптеген жинақталған эксперименталды мәліметтерге қарағанда
ендірілген шектер шамасы тұрақты емес, олар өлшеу жүргізу талаптарына
байланысты. Бұл, әсіресе, қатты денелердің механикалық қасиеттерін кең
аралықта денені жүктеу жылдамдығы, сынау температурасы өзгергенде
периодикалық және вибрациялық жүктеулерде т.б. жағдайларда анық байқалады.
Шектердің тұрақсыздығы, қабылданған механикалық модельдің (жүктелген
жүктеменің атом байланыстарын бірдей кернейтіні) толық еместігі шектердің
тұрақсыздығын түсіндіретін жалпы бір физикалық құбылыстар бар екендігін
байқатады. Ол физикалық құбылыс атомдардың жылулық қозғалысымен байланысты.
Бірақ қатты денелердің беріктілігін зерттеуде, зерттеушілер көп уақытқа
дейін атомдардың жылулық қозғалысын ескермей, атом-молекулалық қирау
концепциясын құрған. Атомның жылулық қозғалысын ескерсек, атом кинетикалық
қирау концепциясы болар еді. Шынында да сыртқы жүктелген күш статикалық
жүйемен әсерлеспей, жылулық тербелісте қозғалатын бөлшек жүйесімен
әсерлесуі керек деп қарастыруға болады. Сол тербелістің арасында атомдар
байланысын кернейтін шама локальді жиі өзгеріп тұрады. Локальді кернейтін
шаманың өзгеруіне аса маңызды роль атқаратын атом жылулық қозғалысының
біртексіздігі, яғни энергетикалык флуктуация. Бұл атом аралықтағы жылулық
флуктуация механикалық құбылыстың сипатын қатты өзгертеді, сонымен бірге
механикалық процестің энергетикасын және оның денелердің басқа
қасиеттерімен байланысын өзгертеді.
Атомдардың жылу қозғалысын ескеріп, денелердің физика-механикалық
проблемаларын қарастыру негізіне молекула-кинетикалық концепция жатады.
Жалпы бұл концепцияны кинетикалық деп атайды.
Бұл қатты денелер беріктілігінің физикалық табиғатын кинетикалық
бағытта зерттеуге эксперименттік және теориялық зерттеулер өткен ғасырда
негізі қаланған. Сол зерттеулердің ішінде Я.И.Френкельдің 1930 жылдары
сұйықтықтар мен қатты денелерде атомдардың жылулық қозғалысы теориясы болып
есептеледі. Бұл теория сол кезде-ақ конденсирланған ортаның көптеген
кинетикалық касиеттерін сипаттауға мүмкіндік тудырған. Атап айтқанда,
тұтқырлық, ағу, диффузия, булану т.б. Бірақ жылулык қозғалыс теориясының
мүмкіншіліктерін беріктіліктің физикалық табиғатын және қатты денелердің
қирау механизмдерін анықтауға көпке дейін қолданбай, дененің беріктілігін
зерттеу механикалық бағытта жалғастырылып дами берген. Қатты денелер қирау
табиғатын кинетикалық бағытта зерттеу тек 1950 жылдары басталған. Ол
академик С.Н.Журков басшылығымен бұрынғы Ленинградтың, қазіргі Санкт-
Петербург қаласындағы А.Ф.Иоффе атындағы физика-техникалық институтында
басталған. Бұл зерттеулер механикалық қирау құбылысына және қатты денелер
беріктілік табиғатына деген бұрынғы көзқарастарды толығымен өзгертті. Бұл
зерттеулер денелердің атомаралық байланысын денеге жүктелген күш
үзбейтіндігін, ол тек жылулық флуктуацияның үзуіне мүмкіндік тудыратынын
дәлелдеді. Сонымен денелердің қирау табиғаты термофлуктуациялық процесс
екендігі анықталды. Яғни, беріктілік шегі деген түсінікті қирау
процесінде қолдануға болмайтындығын көрсетті. Осымен денелердің қирау
кинетикалық теориясы толығымен жетілді деп айтуға болмайды. Әлі де
көптеген анықталмаған және дискуссиялы мәселелер көп. Олар
беріктілік физикасының ары карай даму жолдарын анықтайды және келешекте
қирау кинетикалык концепциясын береді.

1.1. Беріктілік проблемаларды шешуде статикалық және кинетикалық
көзқарастар.
Көп уақытқа дейін қатты денелердің беріктілік физикасының табиғатын
олардың критикалық қирау түсінігімен қарастырып келгенін айтып өттік. Осы
көзқараспен ақауы жоқ идеал дененің морт қирауын қарастырайық. Бұл денеге
жүктелген жүк сол дененің теориялық беріктілігіне жеткенде, ол дене
бірденінен атомдарға шашылып кеткен болар еді. Реал жағдайда денелер
бірнеше бөлікке ғана бөлінетінін және жүктелген жүк шамасы теориялық
беріктілікке жетпей қирайтыны белгілі (Гриффис теориясы). Бұл теорияның рас
екендігін А.Ф.Иоффе өзінің экспериментінде дәлелдеген (NaCl кристалын су
ертінді ортасындағы беріктілігі теориялық беріктілікке жақын болғаны
байқалған). Бірақ Гриффис пен Иоффенің теориясы реал беріктілігінің шамасы
теориялық беріктілік шамасынан төмен екендігін және денелер қирау барысында
2-3 бөлікке ғана бөлінетінін түсіндіргенімен, жүктелген жүктің әсер етуші
уақыт мерзімі сол, жүктелген дененің беріктілік шамасына әсерін тигізуін
түсіндіре алмайды. Мысалы, егер үлгі аз уақыт арасында жүктеліп, оның
беріктілік шегі сол денеден жасалған үлгіні көп уақыт аралығында
жүктелгендегі беріктілік шегіне қарағанда әлдеқайда жоғары екендігі
байқалған. Бұл материалдың статикалық шаршауы деп аталады.
Денелердің статикалық шаршауын көптеген зерттеушілер силикат шыныларда,
полимерлерде, металдарда, ионды кристалдарда т.б. материалдарда байқаған.
Материал беріктілігіне жүктеу уақытының әсерін, әр түрлі жылдамдықпен
жүктегенде немесе деформациялағанда беріктіліктің шегі өзгеруінен,
жылжығыштық тәсілі және ұзақ мерзімді беріктілігін анықтау барысында
байқауға болады. Уақыт мерзімінің дене беріктілігіне әсерін дененің
критикалық қирау сипаттамасымен біріктіруге болмайды. Шынында да бір
жағынан денеге жүктелген жүк белгілі шегіне жеткенде ғана қирайтын болса,
екінші жағынан сол дененің беріктілік шегінің денені жүктеу мерзіміне
(уақытына) тәуелділігі бір-біріне қайшы. Бұл қайшылыққа көптеген
зерттеушілер көңіл аударғанымен, оны түсіндіру барысында статикалық
көзқараста қалып қоя берген. Яғни, дене беріктілік проблемаларының шешімі
болмаған. Мысалы, шыны материалдары беріктілігінің уақытқа тәуелділігін,
Ораван Гриффистің теориясын қолдана отырып, ауадан ылғалды copy арқасында
беттік керілу коэффициентінің төмендеуімен түсіндірген:

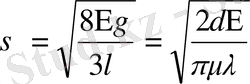
мұндағы Е - Юнг модулі, μ - Пуассон коэффициенті, λ - сызат ұзындығы, γ,δ
- беттік керілу (δ1).
Ораван теориясы бойынша, үлгі тез мерзімде жүктелсе, жаңа пайда болған
сызат ылғалды сорып алуға үлгермейді, сызатта беттік керілу болмайды,
сондықтан да беріктілік жоғары. Ал үлгі көп уақыт мерзімде жүктелген болса,
жаңа сызат ылғалды сорып алуға үлгереді, беттік кернеу сына (клин) ретінде
әсерін тигізіп беріктілік шамасын төмендетеді.
Маргетройд шыны беріктілігіне жүктеу мерзімінің әсерін, шыны екі
фазадан тұруымен байланысты деп түсіндірген. Шыны гетерогенді жүйеден
тұрады деп есептеп (квазитұтқырлы және серпінді элементтерден тұрады),
уақыт мерзімі өткен сайын тұтқырлы пластиктив микробөлшектерде релаксация
өтуі нәтижесінде серпінді элементінде кернеулік өсіп отырады. Бұл процесс
серпінді элементіндегі кернеулік материалдың беріктілік шегіне жеткенше
өседі де, материал қирайды, яғни материалдың беріктілігіне уақыт мерзімінің
әсерін материалдың ішіндегі кернеуліктің таралу процесімен (релаксация)
байланыстырылады. Бұл гипотезаны кейбір зерттеушілер, материал беріктілік
шамасының уақыт мерзіміне тәуелділігін осы күнге дейін осылай түсіндіреді.
Мысалы, поликристалды металдар үшін, әр түрлі физика-химиялық қасиеттері
бар материалдарда олардың беріктілігіне уақыт мерзімі әсерін тигізетіндігі
Ораванның теориясы орынсыз екендігін дәлелдейді. Мысалы, резина,
пластмасса, фарфор, металдар, ионды кристалдар т.б. материалдар зерттелген.
Олардың қирауына және беріктілігіне орта әр түрлі әсер ететіндігі бізге
белгілі.
Сонымен, материалдың беріктілігі уақыт мерзіміне тәуелділігіне зерттеу
жүргізу, ортаға байланысты емес екендігі анықталды. Оған қосымша дәлел,
кейінгі кездегі вакуумда және инертті ортада жүргізген зерттеулер
беріктіліктің уақыт мерзіміне тәуелділігін көрсетеді.
Ораван мен Маргетройдтың теориясы әр түрлі болғанымен, екі теория да
әрбір материалдың беріктілік шегі барлығына қарсы емес. Яғни, беріктіліктің
статикалық концепциясы сақталады, материалдың қирауы критикалык түрде өтеді
деп есептеді. Беріктіліктің уақыт мерзіміне тәуелділігін сыртқы қосымша
процестермен байланыстырады. Алдағы қарастырылатын феноменологиялық және
жүктелген денедегі өтетін элементар процестерді зерттеу нәтижесінде дене
беріктілігінің уақыт мерзіміне тәуелділігі сыртқы қосымша процестермен
байланысты болмай, беріктіліктің уақытқа тәуелділігі - тікелей дененің
қирау механизмімен байланысты екендігін дәлелдеді.
Сонымен, беріктіліктің уақытқа тәуелділігі, қатты денелердің қирау
заңдылығы, жалпы физикалық табиғаты бар және сол табиғатпен тікелей
байланыстылығын көрсетеді. Дене беріктілік проблемасына кинетикалық
көзқараспен қарау, дене қирауы уақытқа байланысты дене ішінде қирау процесі
жүріп, олардың жинақталуымен байланыстыру қажет. Олай болса, бұл
процестерді анықтаудың ең оңай жолы – қатты денелердің жарамдылъқ мерзімін
тұрақты температурада және тұрақты кернеуде анықтау. Яғни, дене жүктелген
уақыттан бастап, сол дененің сол жүктің астында қирау үшін кеткен уақытты
анықтау болып табылады. Материалдың механикалық беріктілігін анықтауда,
кинетикалық қирау концепциясы бойынша материалдың жарамдылық мерзімі -
фундаментальді шама болып есептеледі. Бұл шаманы қирау процесінде орташа
қирау жылдамдығына кері пропорционал деп алуға болады:

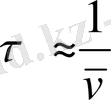
Әрбір материалдың беріктілік қасиетін және олардың қирау табиғатын
кинетикалық көзқараспен анықтау үшін, ол материалдың жарамдылық мерзімінің
жүктелген кернеулікке және үлгіні сынау температурасына тәуелділігін
анықтау қажет:

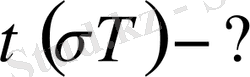
1.2 Қатты денелердің жарамдылық мерзімі және беріктілік кинетикалық
концепциясының негіздері.
Жүктелген қатты денелердің жарамдылық мерзімін, негізінде, үлгіні бір
бағытта созу арқылы анықтаған. Ол үшін үлгіні пленкадан немесе фольгадан не
болмаса топталған талшықтардан арнайы жасайды. Үлгі полимер пленка тәрізді
болса, металл жұқа фольга тәрізді болса, арнайы пышақ арқылы жасалады:
Топталған талшық болса:

Ал кристалдардан талшық параллелепипед жасалып (арнайы пышақ арқылы)
желімге отырғызылады.
Жасалған үлгілерді былай сынайды: белгілі температурада үлгіні, белгілі
кернеулікпен жүктейді. Үлгі жүктелген кезден бастап, үлгі қирағанға дейінгі
уақытты, яғни жарамдылық мерзімін анықтайды. Әр түрлі температурада және
кернеулікте (80-90) үлгілердің жарамдылық мерзімі анықталады, бірақ үлгі
үшін кернеу де, температурада тұрақты болуы қажет.
Арнайы қондырғы, үлгіні созу барысында оның деформациялануына қарамай,
үлгі қирауына дейін жүктелген кернеуді тұрақты етіп ұстайды. Осы
қондырғылардың арқасында жарамдылық мерзім 10 рет аралығында анықталған (10-
3 с - бірнеше ай аралығында).
Жарамдылық мерзімнің температураға, жүктелген кернеулікке тәуелділігі
көптеген материалдар үшін анықталған. Олар: поликристалды металдар -
Санфирова, Бетехтин; әр түрлі монокристалдар - Бақтыбаев; металл емес
қоспалар - Регель, Левин; полимерлер — Журков, Нарзуллаев, Аббасов; металды
қоспалар – Бетехтин, Петров, Бақтыбаев; күрделі компазитты материалдар –
Регель, Бетехтин, Бақтыбаев; цемент тастар, бетондар - Бақтыбаев,
Кадырбеков.
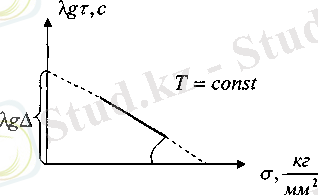
Барлық зерттелген материалдар үшін температура тұрақты болған кезде,
жарамдылық мерзімнің кернеулікке тәуелділігін былай жазуға болады:
(1)
осы материалдың тұрақты шамасы:

Жарамдылық мерзім ортаға байланысты емес екенін дәлелдеу үшін,
зерттеуді вакуумда не болмаса инертті ортада жүргізген. Бұл формуланы
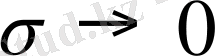болған кезде қолдануға болмайды, себебі сызықты 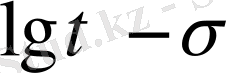тәуелділік
орындалмайды. Оның себептерін кейін карастырамыз.
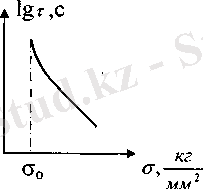
Кейбір зерттеушілер, мысалы, И.А.Одинг және басқалар 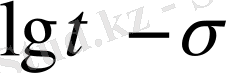қисығы
асимтотикалық ординатаға жетпей, ординатаға параллель оське жақындайды,
қауіпсіздік кернеу деп есептеген. Бұл көзқарасты тексеру өте қиын,
өйткені кездегі жарамдылық мерзімі өте үлкен шама. Бұл
көзқарас теорияға қарсы болмағанымен дискуссиялық көзқарасқа жатады. Сол
үшін біз қазірше тек 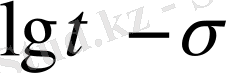тәуелділіктің тура сызықты жағын қарастырамыз.
Барлық зерттелген материалдарға бұл теңдеудің орындалуы, жарамдылық мерзім
жүктелген денеде өтетін қирау процесінің жинақталуына кетеді деп есептеуге
болады. Бұған дәлел, үлгіні жүктеуді бірнеше рет тоқтатып, қайтадан сол
шамаға жүктеген кездегі қирауға кеткен жарамдылық мерзім, тоқтаусыз үзбей
жүктеген кездегі жарамдылық мерзімге қарағанда аз болғаны дәлел бола алады.
Енді жүктелген денедегі өтетін процестер, сол дененің қирауына алып
келетін болса, сол процестің табиғатын анықтау мақсатында жарамдылық мерзім
шамасына температураның әсерін анықтау қажет. Сонымен, тәуелділігін
әр түрлі температурада анықталған. Әр температураның тәуелділігі тура
сызықты, температура өскен сайын қисығы енкіштігі ұлғайып, температура
төмендеген сайын сызығы тік сызыққа жақындайтыны байқалған. Бұны
график түрінде былай көрсетуге болады:

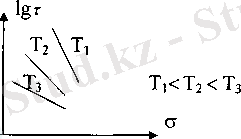
Белгілі бір жарамдылық мерзім шамасында барлық сызықтар бір
нүктеге қосылатындығы байқалған. Ол жарамдылық мерзім тең.
Сызықтардың қосылатын нүктесін полюс деп атаған. График түрде былай
көрсетуге болады:

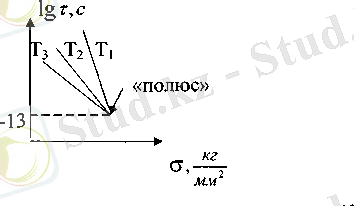
Жарамдылық мерзімнің полюстағы шамасы
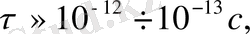
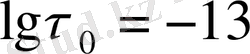
Жарамдылық мерзімнің Т, тәуелділігін аналитик түрде былай жазуға
болады:
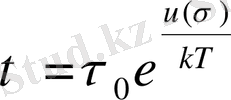(2),
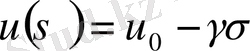
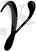және и0 - тұрақты шамалар, олардың физикалық мәнін кейін
қарастырамыз. Екінші формуланың экспериментті нәтижелерді тура
түсіндіретінін тексеру үшін, бұл формуланы былай жазуға болады:
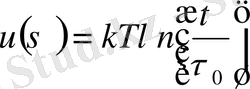(3)
Бұл формулаға қарағанда барлық тура сызықтар бір сызыққа:
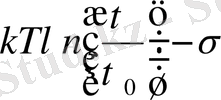жинақталуы қажет. Дененің қирау табиғатын (2)-формуланы талдау арқылы
анықтауға болады. Бұл формула жарамдылық мерзімнің негізгі теңдеуі болып
есептеледі.

1.3. Жарамдылық мерзімді анықтау тәсілі.
Жоғарыда айтылғандай материалдың жарамдылық мерзімін бір бағытта үлгіні
тарту (созу) арқылы анықталады. Ол үшін үлгі біртекті деформацияланып,
көлемі өзгермейтін жағдайда үлгінің көлденең кескіні деформацияның
арқасында былай азаяды:

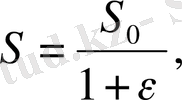
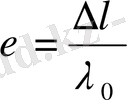
Олай болса, үлгіге әсер етуші кернеу өсуі 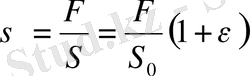болады. Үлгіге әсер
етуші кернеу тұрақты болу үшін, жүктелген күш деформация барысында былай
кемуі керек:

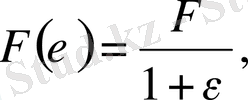
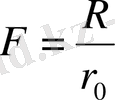
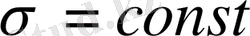болу үшін ілінген Р жүктің иығы 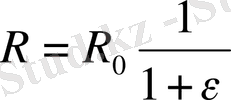шамаға өзгеріп тұруы керек. R-
дің деформация барысында мұндай өзгеруін Э.Е.Томашевский және А.И.Слуцкер
есептеп тапқан рычаг фигурасының профилі, полярлық координат бойынша былай
болу қажет:

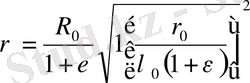
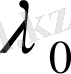- үлгінің бастапқы үзындығы.

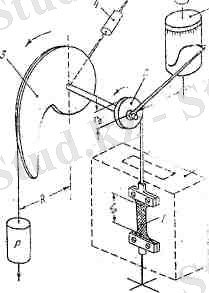
1-сурет. Жарамдылық мерзімді анықтайтын қондырғының схемасы. 1-үлгі, 2-
блокпен иілгіш, 3-фигуралы рычаг, 4-фигуралы рычагты теңестіретін ауырлык,
5-ішінде сағат механизмі бар барабан, жылу излояцияланбайтын камера.
Рычагтың (1-сурет) негізгі параметрі 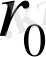сыналатын материалдың
қасиетіне байланысты. Егер материалдың деформациясы көп болмаса,
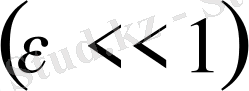
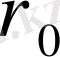радиусты үлгі ұзындығы 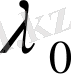тең етіп алуға болады. Егер деформация
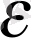
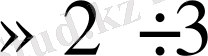болса .
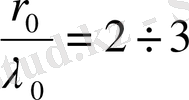Практикада рычагты деформация барысында 2700 бұрышқа бұру мүмкін.
Рычагты дайындау дәлдігін асыру мақсатында рычаг өлшемдері үлкен болуы
қажет. Сол себепті 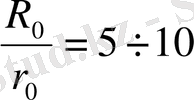аралығында болады.
Бұл қондырғы арқылы жарамдылық мерзімді бірнеше секундтан, бірнеше ай
аралығында анықтауға болады. Жарамдылық мерзімді анықтауда төменгі жағынан
шектеулі қондырғының конструкциясына байланысты, үлгіні жүктеуге кететін
уақыт 2-3 секундты талап етеді. Ал жарамдылық мерзімнің Т-ға
тәуелділігін дәл анықтау үшін, жарамдылық мерзімді өлшейтін интервал үлкен
болуы қажет. Бірақ интервалды үлкейту, яғни айдан жылға өту перспективасыз,
себебі өлшеу интервалы бір реттікке ғана өседі. Ал қысқа жарамдылық
мерзімді анықтау, мысалы, 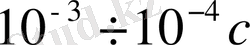жарамдылық мерзім интервалын 3-4 ретке
кеңітеді. Сонымен қатар, материалдардың соққы (удар) жүктелуінде қирауы
практикада көп кездескен себепті, бұл бағытта кирау барысын зерттеу қажет
болатындығы белгілі.
Сонымен, үлгіні қысқа уақыт аралығында жүктеу тәсілін табу қажет. Ол
үшін кіші интервалды өлшейтін жүйе табу керек. Тез өтетін механикалық
процестерді зерттеуге инерциясыз электр өлшеу тәсілдері қолданылады. Бұл
электр тәсілінің негізгі элементі болып, электр сигналын беретін
көрсеткіштер (датчиктер) жатады. Көрсеткіштер арқылы механикалық шамалар
анықталады. Көрсеткіштердің түрлері көп (А.М.Туричин,
Электрические измерения не электрических величин). Көрсеткіштен пайда
болған сигналдар күшейтіріліп, катод не болмаса шлейфті осциллограф арқылы
тіркеледі. Аз шамадағы жарамдылық мерзімді өлшейтін қондырғыны
электродинамикалық тартып цирату машинасы деп атайды. Бұл машина бірінші
рет Санкт-Петербург қаласындағы физика-техникалық институттың, беріктілік
физикасы зертханасында С.Н.Журков басшылығымен Э.Е.Томашевский құрастырған
(2-сурет).

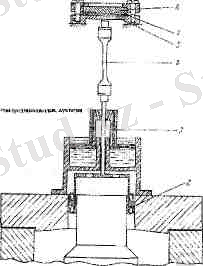
2-сурет. Кіші мөлшердегі жарамдылық мерзімді өлшейтін қондырғының схемасы.
1-саңлауы бар магнит, 2-үлгімен косылған катушка, 3-сұйыктық демпфер, 4-
үлгі, 5-күш датчигінің мембранасы, 6-датчиктің екінші электроды, 7-мембрана
мен конденсатордың арасына қойылған смодадан жасалған сақина.
Бұл қондырғының негізін сыйымдылық күш көрсеткіші және сұйық демпферлі
электродинамикалық жүктегіш кұрайды. Үлгіні жылдам жүктеу
электродинамикалық қондырғы арқылы жүргізіледі. Электродинамикалық қондырғы
сақина тәрізді саңылауы бар магниттен(І) тұрады. Сақина тәрізді саңылауға
сынайтын үлгімен қосылған катушка орналасқан. Саңылауда магнит өрісі
магниттелген коэрцитивті қоспа арқылы не болмаса магниттеуші катушка(2)
арқылы жасалады. Қозғалатын катушкадан электр тогы еткенде, мынаған тең
Ампер күші пайда болады:

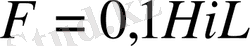
мұндағы: Н-магнит өрісінің кернеулігі, і-катушкадан өтетін
ток, L-катушканың ұзындығы.
Бұл күш үлгіні жүктеуге қолданылады. Катушканың қозғалу үдеуі, ауырлық
үдеуінен 100 есе үлкен болуы мүмкін. Үлгі мен катушка
аралығында сұйықтық демпфер(З) орналастырылады. Ол арқылы әсер ететін күш
импульсінің формасын (3-сурет) өзгертуге болады.

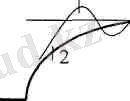
3-сурет.Үлгіні бір бағытта тарту күші өсуінің осциллограммасы. 1-демпфер
жоқ кездегі кернеудің өзгеруі, 2-демпфер қосылған кездегі кернеудің
өзгеруі.
Демпфер үлгіні жүктеу диаграммасын өзгертеді екен. Демпфер арқылы
үлгіні тербеліс режим жүктеуден апериодикалық жүктеуге болады. 2-ші
сызықтың формасын демпфердің үйкеліс коэффициентін өзгерту арқылы жасауға
болады. Үлгіге әсер етуші күштің өсуі аралығында жатады. Жүктеу
уақытының шектелуі колданған тәсілдің мүмкіншілігінде емес, ол зерттелетін
материалдың қасиетіне және серпінді импульстің үлгі бойымен таралу
жылдамдығына байланысты, яғни табиғатты шектелу болып есептеледі. Жүктеу
уақытын қысқарту үшін, тек үлгінің ұзындығын қысқарту арқылы болады.
Сонымен бұл қондырғы жоғары жиілікті сыйымдылықты күш күшейткіштен,
жоғары жиілікті лампалы генератордан, детекторлайтын схемадан және катодты
осциллографтан тұрады. Бұл электродинамикалық машинаны созылу деформациясы
аз материалдардың жарамдылық мерзімін анықтауға () болады. Пластикалық
деформациясы жоғары материалдарға қолдану үшін электродинамикалық жүктейтін
бөлшек, жүктелген кернеулік шамасын автоматты түрде деформация барысында
тұрақты етіп үстап тұруы кажет ( = const). Ол үшін саңылауда
қозғалатын катушка біртексіз арнайы орамнан жасалуы қажет не болмаса
саңылауда арнайы біртексіз магнит өрісін жасау қажет. Бүгінгі таңда ондай
қондырғы тәсілін ешкім жасамаған. Материал беріктілігіне ортаның әсерін
анықтау үшін, басқаша айтканда Ораванның теориясын тексеру үшін Журков,
Левин, Томашевский бірінші рет вакуумда және инертті ортада зерттеу
жүргізді.
Олардың зерттеуі бойынша, беріктіліктің уақытқа тәуелділігі тек ортаға
тәуелді еместігін дәлелдейді. Вакуум жасайтын жүйе форвакуум сорғыштан
(насос) - ВН-461 және май булы сорғыштан (парамаслянный) - ЦВЛ-100 тұрады.
Қалған бөлшектері материалды жүктеу және кернеулікті тұрақты ұстайтын
бөлшектер.

1.4 Күрделі жағдайда материалдардың жарамдылық мерзімін анықтау
тәсілдері.
Біз материалдарды бір бағытта тарту тәсілімен жарамдылық мерзімін қалай
анықталатынын қарастырдық. Бұл қарапайым тәсілден басқа, материалдарды
күрделі жағдайда сынау зерттеулері де жүргізілген. Күрделі сынауға
материалдарды циклды жүктеу, бұрау, бұрап тарту, гидростатикалық қысым
ортасында, радияцияның әсері, әр түрлі сұйық орталарда зерттеулер жатады.
Біз бұл тәсілдерге қысқаша тоқталып өтеміз, себебі, әрбір тәсілдің
практикада өзінің орны бар. Бірақ материалдардың қирау процесін физика
негізінде анықтауға аса айтарлықтай үлес қоспайды. Сонымен материалдардың
шаршау тәсіліндегі жарамдылық мерзімі қалай анықталатынына тоқталамыз.
Валға отырғызылған эксентристі моторға қосып, кривошип-шатун механизмі
серіппені (пружина) тартып, демпфер арқылы үлгіге және динамометрге жүк
түсіреді (4-сурет).

4-сурет. Үлгіні циклді жүктейтін қондырғының схемасы. 1-мотор, 2-
эксцентрик, 3-кривошипті шатун механизмі, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.