Тейлор формулаларының жалпы жағдайы: көпмүшелік жуықтауы, қалдық және Лагранж формуласы

Пән: Математика, Геометрия
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 4 бет
Таңдаулыға:

Тейлер формулалары (жалпы жағдай) . Енді жалпы жағдайға көшелік. 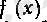функциясы аралығында анықталып, х _о <=1 нүктесінде 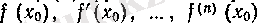туындылары бар болсын.

(х) функциясын жуықтау құралы ретінде сәйкес туындылары I (х) функциясының Хо нүктесіндегі туындыларымен беттесетін п дәрежелі көпмүшелікті, яғни (6) көпмүшелігін алайық. Ол / ( ^х ) функциясының нүктесіндегі Тейлор көпмүшелігі деп аталады.

Егер (х) функдиясы п дәрежелі көпмүшелік болса, онда әрбір 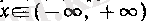үшін 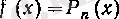-бұл алдыңғы пунктте дәлелденген еді) .

Басқа жағдайларда ондай теңдік орындалмауы мүмкін, демек цателік немесе мүше деп аталатын

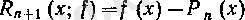
фуикциясын карастыруымыз қалсетті.

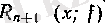функциясының

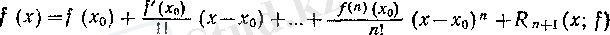
анықтамаеынан шығатын формуласын Тейлор формуласы деп атайды.

Негізгі мәселе 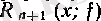өрнегінен пайдалы қорытындылар

жасау мүмкін болатын (мысалы, белгілі мағынада кішкене болуы огуралы мәлімет алу) түрін табу болады.

Бұл мәселе кейбір дербес жағдайларда бұрын шешілген еді. Біріншіден, егер (х) функциясы сегментінде дифференциалданса, онда оның түрі Лагранж теоремасы бойынша

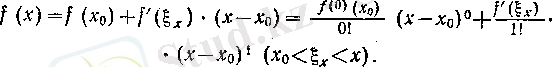
яғни 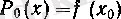ноль дәрежелі көпмүшелік,

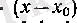болады. Екіншіден, егер (х) функциясы

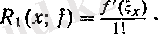
х ₀ нүктесінде үзіліссіз болса, онда 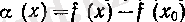үшін

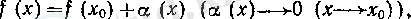
яғни 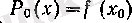- ноль дәрежелі кепмүшелік, ал

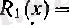
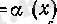қалдығы болғанда нольге ұмтылады. Үшіншіден,

егер } (х) функциясы х ₀ нүктесінде дифференциалданса, онда

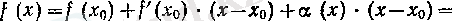
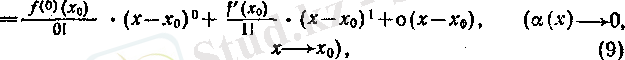
яғни 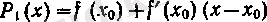- 1-дәрежелі көпмүшелік, а л

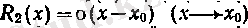болады.

Осыған орай түрлері бірдей болса да, олардың орындалуының шарты мен қолдану жағдайлары бір-бірінен өзге болатын Тейлордың екі формуласы бар. Біріншісі, Лагранж теоремасы-ның жалпылауы болатын келесі Тейлор формуласы. п теріс емес бүтін. және р оң сандары берілсін. (х) функциясының сегментінде п-ретті туындысы бар және үзіліссіз болып, (а) интервалында (п+1) -ретті туьшдысыбар болсын. Онда [а, б] сегментінің бір-бірінен өзге болатын кез келген х жәнё х ₀ нүкте-лері үшін

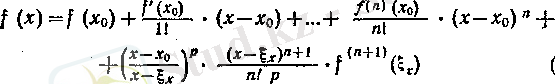
теңдігін қанағаттандыратын х ₀ ыт х-тың арасында жататын % _х нүктесі бар болады. Екіншісі, шек тапқанда және асимптотика-лық (эквиваленттік) жіктеулерді есептегенде қолданылатын, функцияның нүктенің «қасындағы» қүрылысын анықтайтын ке-лесі Тейлордың локальді формуласы: п оң бүтін саны беріліп _э / (х) функциясьшьщ #о нуктесінде п-реттІ туындысы бар болса, онда

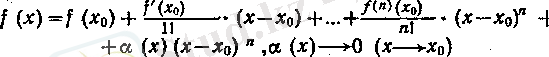
болады. Сонымен, х нүктесі Хо-те жақындаған сайын, ( (х) функ-циясынын, өзінің Тейлор көпмүшелігінен өзгешелігі нольге {х-'Хо) ^п функциясына карағанда жылдам үмтылады.

(10) формуласы (7) формуласына, ал п=0 және п=1 болғанда

(11) формуласы сәйкес (8) және (9) формулаларына айналады.

Бұл теореманың ерекшелігі мынада: функцияда К _о нүктесінің өзіңде туындысы бар болуы оның ойлаған маңайында туындысы бар болуынан шығады.

Теорема: f функциясы [x _o , x _o -g] сегментінде үзіліссіз болып, (x _o , x _o + g) интервалында дифериенциясын (б>о) . Егер 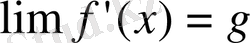шегі бар болса (g-нақты сан, + не 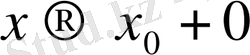-- ) онда f функциясының х нүктесіне оң жақтағы туындысы бар болып, сол шекке тең болады, яғни

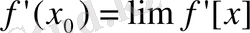
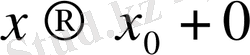
Дәлелдеуі: Әрбір x ₀ <x< x ₀₊ б үшін [x ₀ x] сегментінде қолданлған. Логранж формуласы бойынша

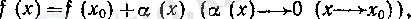
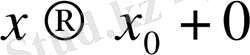Теңдігіә орындалады. болғанда болады. *, демек (10) теңдігінің оң шағындағы өрнектің шегі Q болады. Сондықтан (10) сол жағындағы өрнектің де 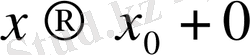болғанда шегі бар болып, Q тең болады. Яғни .

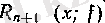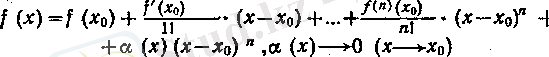
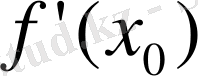Әрине, дәл осындай тұжрым сол жақты туывнды үшінде дұрыс бплады. Яғни бұл теолремада функциясының келесі тамаша қасиетішығады.

Солар функциясы (а, в) интервалдан деференциялдансын. Онда 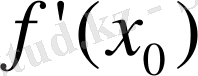функциясыныңбірінші түдегі үзіліс нұктелері болмайды, .

Дәлелдеуі 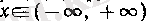болсын. Онда келесі үш жағдай мүмкін.

Бірінші. 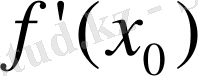функциясы х ₀ нүтесіне үзіліссіз.

Екіншісі. 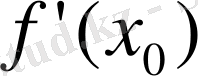функциясы х ₀ нүктесінде екінші түрде үзілісті, үшіншісі 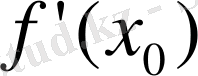нүктесінде бірінші түрде үзілісті.

Соңғы жағдай ешқашанда орындалмайтының көрсетейік. Ресында да, 3) жағдай орындалса онда lim 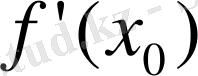және

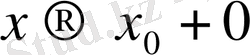
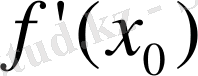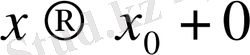
мен онда lim шептері бар болып кемінде біреуі 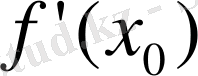-ге тең болмауы керек. Анықтақ үшін

lim

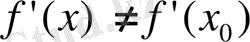
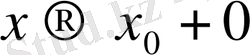
болсын. (9) бойынша (12) -нің сол жағындағы шек 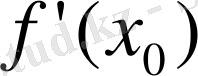бірінші түріндегі үзіліс нүктелері жоқ.

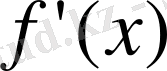екінші түрдегі үзіліс нүктесі бар болуы мүмкін.

Мысалдар. 1. 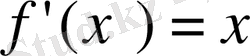функциясы сегментінде анықталған және үзіліссіз. 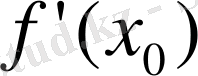элемент функциясы болсада оның туындысы +1 және -1 нүктелерінде негізгі элементтер функцияларының туындылардың таблицасы мен дефференциялау ережелерін пайдаланып табуға болмайды. Өйткені ол нүктелерде екі қозғалғыштың да ақырлы туындылары жоқ.