Теңдеулер: бір айнымалысы бар сызықты теңдеулер, екі белгісізі бар сызықтық жүйелер және біртекті жүйелердің қасиеттері мен шешу әдістері


Жоспар
- Теңдеу
- Бір айнымалысы бар сызықты теңдеу және оның қасиеттері
- Екі белгісізі бар сызықтық теңдеу және олардың шығарылуы
- Біртекті жүйелер және оларға қолданылатын амалдар
- Теңдеу
Құрамында әріппен белгіленген белгісізі (айнымалысы) бар теңдік теңдеу деп аталады.
Мысалы,
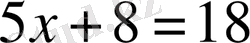 ;
;
 ;
;
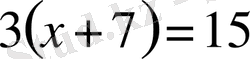 - теңдеулер.
х
- белгісіз (айнымалы) . Мұндай теңдеулерді бір белгісізі бар немесе
бір айнымалысы бар теңдеулер
деп атайды.
- теңдеулер.
х
- белгісіз (айнымалы) . Мұндай теңдеулерді бір белгісізі бар немесе
бір айнымалысы бар теңдеулер
деп атайды.
Теңдеудің оң жағы және сол жағы болады. Мысалы,
 теңдеуіндегі
теңдеуіндегі
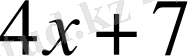 - теңдеудің сол жағы, ал 19-теңдеудің оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады. 4
х
; 7; 19 - мүшелер. Мұндағы 4
х
- белгісізі бар мүше, 7, 19 - бос мүшелер.
- теңдеудің сол жағы, ал 19-теңдеудің оң жағы. Теңдеудегі алгебралық қосылғыштардың әрқайсысы оның мүшелері деп аталады. 4
х
; 7; 19 - мүшелер. Мұндағы 4
х
- белгісізі бар мүше, 7, 19 - бос мүшелер.
Теңдеумен берілген мысалдар мен есептерді шығарғанда, ондағы әріппен берілген белгісіздің немесе айнымалының сан мәнін табамыз. Демек, теңдеудің түбірін табамыз.
Белгісіз санның немесе айнымалының теңдеуді тура санды теңдікке айналдыратын мәні теңдеудің түбірі деп аталады.
Теңдеуді шешу дегеніміз - оның түбірлерін табу немесе түбірлерінің жоқ екенін дәлелдеу.
Теңдеулерді шешкенде, кейде түбірлері бірдей болатын теңдеулерде кездеседі. Түбірлері бірдей болатын теңдеулерді
мәндес теңдеулер
деп атайды. Мысалы,
 теңдеуі мен
теңдеуі мен
 және
және
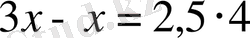 теңдеулері - мәндес теңдеулер. түбірлері бірдей:
теңдеулері - мәндес теңдеулер. түбірлері бірдей:
 . Ескеретін жағдай, кейде теңдеудің түбірі болмайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады.
. Ескеретін жағдай, кейде теңдеудің түбірі болмайды. Түбірлері болмайтын теңдеулер де мәндес теңдеулер болып саналады.
Теңдеу - әрпі бар теңдік болғандықтан, теңдеудің қасиеттерін теңдіктің қасиеттеріне сүйеніп дәлелдейміз.
Теңдеулердің 1-қасиеті.
Теңдеудің екі жағына да бірдей санды немесе әріпті өрнекті қосқанда (азайтқанда) теңдеу мәндес теңдеуге түрленеді.
1-мысал.
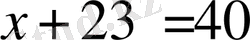
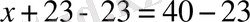

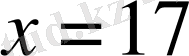 - теңдеудің түбірі.
- теңдеудің түбірі.
Мысалда теңдеулердің бұл қасиетін қолдану нәтижесінде 23 саны теңдеудің сол жағынан қарама-қарсы таңбамен оң жағына көшірілді. Онда теңдеулердің 1-қасиеті бойынша:
теңдеудегі қосылғыштың таңбасын қарама-қарсыға өзгертіп, оны теңдеудің бір жағынан екінші жағына көшіргенде теңдеу мәндес теңдеуге түрленеді.
Теңдеуді мұндай түрлендіруді енгізген ІХ ғасырдағы Орта Азия ғалымы Мұхаммед бен Мұса аль-Хорезми. «Алгебра» атауы оның «Китаб аль-джебр валь-мукабала» атты шығармасынан алынған. Теңдеулердің 2-қасиеті:
теңдеудің екі жағында нөлден өзге бірдей санға көбейткенде немесе бөлгенде теңдеу мәндес теңдеуге түрленеді.
2-мысал.
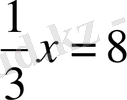 Қысқаша:
Қысқаша:
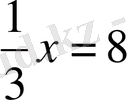
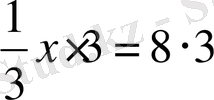
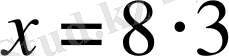
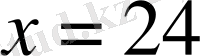
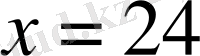
2. Бір айнымалысы бар сызықтық теңдеу және
оның қасиеттері
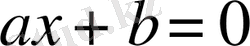 (мұндағы
(мұндағы
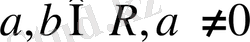 ) түріндегі теңдеу
бір айнымалысы бар сызықтық теңдеу
деп аталады.
) түріндегі теңдеу
бір айнымалысы бар сызықтық теңдеу
деп аталады.
1. Теңдеудің түбірлерін табу: S теңдеудің шешімдер жиыны болсын.
1) Егер
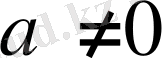 болса,
болса,
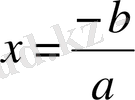 ,
,
2) Егер
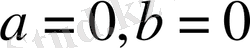 болса, теңдеудің шексіз шешімі
болса, теңдеудің шексіз шешімі
 болады.
болады.
3) Егер
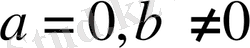 болса, теңдеудің шешімі болмайды
болса, теңдеудің шешімі болмайды
 .
.
2. Теңдеудің қасиеттері:
1)
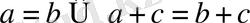
Теңдеудің екі бөлігіне де бірдей санды қосуға болады.
2)
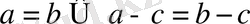
Теңдеудің екі бөлігінен бірдей санды азайтуға болады.
3)
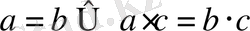
Теңдеудің екі бөлігінен бірдей санға көбейтуге болады.
4)
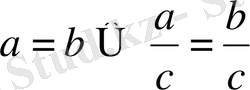
Теңдеудің екі бөлігін нольден өзгеше санға бөлуге болады.
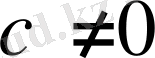
5)
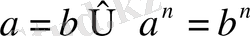
Теңдеудің екі бөлігін бірдей дәреже шығаруға болады.
6)
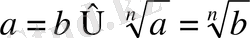
7)
 және
және
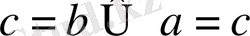
Егер екі сан үшінші санға тең болса, онда бастапқы екі сан өзара тең болады.
3. Екі белгісізі бар сызықтық теңдеулер және
олардың шығарылуы
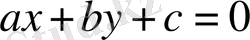 түріндегі теңдеу (мұндағы
түріндегі теңдеу (мұндағы
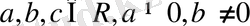 )
екі белгісізі бар сызықтық теңдеу
деп аталады.
)
екі белгісізі бар сызықтық теңдеу
деп аталады.
1) Теңдеулер жүйесін шешу:
а) Екі белгісізі бар теңдеудің шексіз көп шешімі болады.
б)
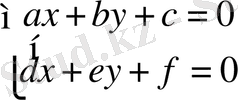 Теңдеулер жүйесін шешкенде 3 түрлі жағдай болуы мүмкін:
Теңдеулер жүйесін шешкенде 3 түрлі жағдай болуы мүмкін:
1) Егер
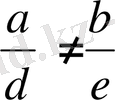 болса, бір шешімі болады,
болса, бір шешімі болады,
2) Егер
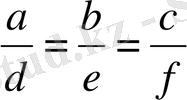 болса, шексіз көп шешімі болады,
болса, шексіз көп шешімі болады,
3) Егер
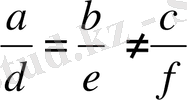 болса, теңдеулер жүйесінің шешімі болмайды.
болса, теңдеулер жүйесінің шешімі болмайды.
Ескерту: Екі белгісізі бар сызықты теңдеуді түзумен кескіндеуге болады.
1-ші жағдайда түзулер қиылысады.
2-ші жағдайда түзулер беттеседі.
3-ші жағдайда түзулер параллель болады.
1- мысал:
Теңдеуді шешіңіз
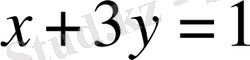 .
.
Шешуі:
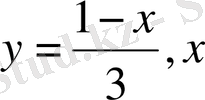 - ке мән бере отырып
y
- тің сәйкес мәндерін таба аламыз. Шексіз шешімі болады.
- ке мән бере отырып
y
- тің сәйкес мәндерін таба аламыз. Шексіз шешімі болады.
2-мысал: Теңдеулер жүйесін шешіңіз:
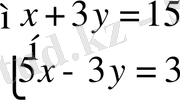
Шешуі: 1-ші тәсіл (Ауыстыру тәсілі) :
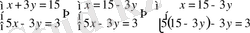
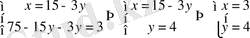
Жауабы:

2-ші тәсіл (Қосу тәсілі) :
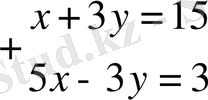
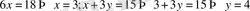 .
.
Жауабы:

3-мысал: Теңдеулер жүйесін шешіңіз:
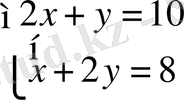
Шешуі:
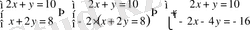
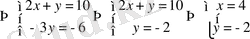
Жауабы:

- Біртекті жүйелер және оларға қолданылатын амалдар
1-мысал.
Мына жүйені шешіңдер
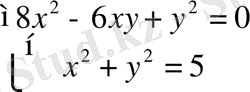
Шешуі:
Ескерейік берілген жүйедегі
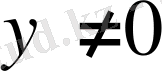 шарты орындалуы керек. Негізгі шарттағы жүйеде
шарты орындалуы керек. Негізгі шарттағы жүйеде
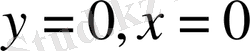 екінші теңдікті қанағаттандырмайды. Бірінші теңдікті
х
2
-қа бөлеміз. Шыққан теңдік
екінші теңдікті қанағаттандырмайды. Бірінші теңдікті
х
2
-қа бөлеміз. Шыққан теңдік
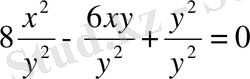 немесе
немесе
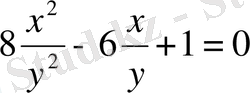 .
.
Ықшамдау үшін
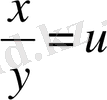 деп белгілейміз. Өрнек түрін өзгертеді
деп белгілейміз. Өрнек түрін өзгертеді
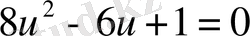 . Бұл квадрат теңдеуге келеді, түбірлері:
. Бұл квадрат теңдеуге келеді, түбірлері:
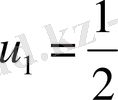 және
және
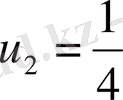 . Солай бірінші белгілегенімізді аламыз,
. Солай бірінші белгілегенімізді аламыз,
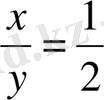 , не
, не
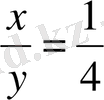 .
.
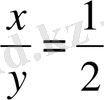 : Бұл жерден
y=2x
. екінші теңдіктен
: Бұл жерден
y=2x
. екінші теңдіктен
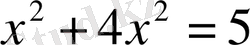 ,
,
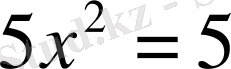 х
1
=1
; х
2
=1.
х
1
=1
; х
2
=1.
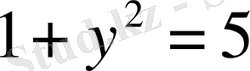
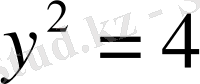 у
1
=1;
у
2
=1.
у
1
=1;
у
2
=1.
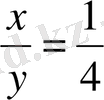 : Екіншісіде
y=2x
біріншісіне сәйкес:
: Екіншісіде
y=2x
біріншісіне сәйкес:
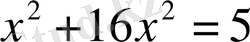 ,
,
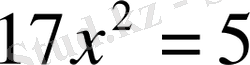 ,
,
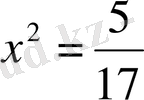 ,
,
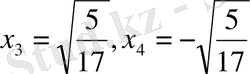 .
.
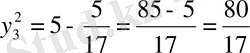
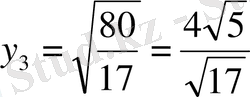
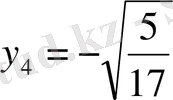
Жүйенің бірінші теңдеуін осы теңдеуге енетін қосылғыштардың дәрежелері бірдейекіге тең
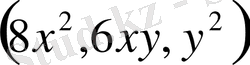 болғандықтан
болғандықтан
 түріндежазуға болады.
түріндежазуға болады.
Әрқайсысы мүшесінің дәрежелері k - ға тең болатын х және у айнымалылы көпмүшелік k дәрежелі біртекті көпмүшелік деп аталады.
Егер
Р(х, у)
-
k
дәрежелі біртекті көпмүшелік болса,
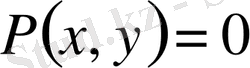 түріндегі теңдеу х және у -ке қатысты біртекті
k
дәрежелі теңдеудеп аталады.
х
және
у
-ке қатысты у
k
-ға бөлінетін (егер
y=0
теңдеудің түбірі болмаса) біртекті теңдеу
түріндегі теңдеу х және у -ке қатысты біртекті
k
дәрежелі теңдеудеп аталады.
х
және
у
-ке қатысты у
k
-ға бөлінетін (егер
y=0
теңдеудің түбірі болмаса) біртекті теңдеу
 белгісізді теңдеуге түрленеді. Біртекті теңдеудің бұл қасиетінің көптеген мәселелерді шешуде маңызы зор.
белгісізді теңдеуге түрленеді. Біртекті теңдеудің бұл қасиетінің көптеген мәселелерді шешуде маңызы зор.
2-мысал.
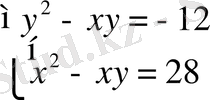 теңдеулер жүйесін шешейік.
теңдеулер жүйесін шешейік.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz