Дифференциалдық теңдеулердің қалыпты жүйесі: теориясы, Коши есебі және параметрлік тәуелділік


КІРІСПЕ. . . .
- Дифференциалдық теңдеулердің қалыпты жүйесінің жалпы теориясы
- Дифференциалдық теңдеулер жүйесінің түрлері. Қалыпты жүйе, оны жоғарғы ретті теңдеуге келтіру . . .
- Қалыпты жүйенің векторлық түрде жазылуы. Қысатын бейнелеу қағидасын қолданып, Коши есебі шешімінің бар және жалғыз болу туралы теореманы дәлелдеу . . .
- Коши есебі шешімінің параметр мен бастапқы берілгендерден тәуелділігі . . .
- Қалыпты жүйенің интегралдары және олардың қасиеттері . . .
- Дифференциалдық теңдеулердің симметриялық жүйесі . . .
Есептер . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
3
5
5
11
15
24
33
37
42
43
Мазмұны
Кіріспе
Көптеген процестердің математикалық түрі, ізделінетін белгісіз шама цифр емес, ал белгілі бір аргументке тәуелді функция ретінде берілетін теңдеумен өрнектеледі. Сонымен қатар, бұл функция өз туындысы және аргументімен байланысты болады. Бұндай теңдеулер дифференциалдық теңдеулер деп аталады. Дифференциалдық теңдеулер математикалық анализ жүргізуде үлкен роль атқарады.
Дифференциалдық теңдеулер - ізделінетін функцияны оның әр түрлі ретті туындыларымен (немесе дифференциалдарымен) және тәуелсіз айнымалылармен байланыстыратын теңдеулер. Дифференциалдық теңдеулер 17 ғасырдың соңында механика, т. б. жаратылыстану пәндерінің талабына сәйкес интегралдық есептеу және дифференциалдық есептеумен қатар пайда болды. Қарапайым дифференциалдық теңдеулер Ньютонның және неміс математигі Лейбництің еңбектерінде кездеседі. “Дифференциалдық теңдеулер” терминін ғылымға Лейбниц енгізген (1676) .
Тәуелсіз бір айнымалыға тәуелді бір немесе бірнеше функциялардың туындылары бар дифференциалдық теңдеулерді
жай дифференциалдық теңдеу
деп, ал тәуелсіз бірнеше айнымалыға тәуелді функциялардың дербес туындылары бар дифференциалдық теңдеулерді
дербес туындылы дифференциалдық теңдеу
деп атайды. Дифференциалдық теңдеулерге енетін туындылардың реті дифференциалдық теңдеулердің реті делінеді.
Зерттеудің өзектілігі: курстық жұмыстың мазмұнының ғылыми құндылығын арттыру және оның негізінде пәнге деген қызығушылығын арттырып, өз бетінше іздену. Білім, білік, дағды алуын қамтамасыз етуге, жеке шығармашылық қабілеті дамуы үшін жағдай туғызу.
Мақсаты: Дифференциалдық теңдеулердің қалыпты жүйесін талдау.
Міндеті:
- Дифференциалдық теңдеулердің қалыпты жүйесінің теориялық бөлімін қарастыру.
- Дифференциалдық теңдеулердің қалыпты жүйесін есептермен мысалдарда қарастыру.
Зерттеу объектісі: Функцияларды дифференциалдау.
Зерттеу пәні: Дифференциалдық теңдеулерді шешу.
Зерттеу әдістері: Талдау нәтижесінде алынған мәліметтерді бақылап, тақырып бойынша әдебиеттерді зерттеу.
Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, практикалық бөлім, қорытынды және қолданылған әдебиеттер тізімінен тұрады.
Қойылған проблеманың актуальдығы: қазіргі кезде техниканың дамуына байланысты әр түрлі химиялық, физикалық заттардың құрамын, массасын, көлемін, ұзындығын, т. б. - параметрлерін зерттеу қажеттігі туып отыр. Одан басқа бұл параметрлердің уақытқа және де т. б. шамаларға тәуелділігін де білу керек. Мұның бәрін тек дифференциалдық теңдеулер жүйесі көмегімен ғана жүзеге асыруға болады.
- Дифференциалдық теңдеулердің қалыпты жүйесінің жалпы теориясы
1. 1 Дифференциалдық теңдеулер жүйесінің түрлері. Қалыпты жүйе, оны жоғарғы ретті теңдеуге келтіру
Дифференциялдық теңдеулер жүйеcі жалпы түрде былай жазылады:
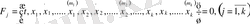 (1) мұндағы
t-
тәуелсіз айнымалы,
(1) мұндағы
t-
тәуелсіз айнымалы,
 ізделінетін функциялар, ал
ізделінетін функциялар, ал
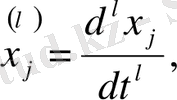
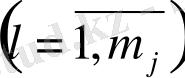 ,
,
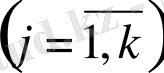
Біз теңдеулердің саны ізделінетін функциялар санына тең болатын жағдайды қарастырамыз. Жүйедегі
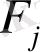 ,
,
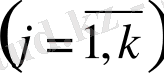 функциялары
функциялары
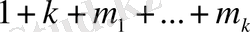 айнымалылардан тәуелді. Олар осы
айнымалылардан тәуелді. Олар осы
 айнымалыларының кеңістігінде жататын қандай да бір
D
облысында анықталған.
айнымалыларының кеңістігінде жататын қандай да бір
D
облысында анықталған.
Дифференциалдық теңдеулер жүйесін әдетте
дифференциалдық жүйе
деп атайды. Жүйеге кіретін
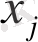 ен жоғарғы реті жүйенің
ен жоғарғы реті жүйенің
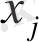 ,
бойынша реті
деп аталады, ал
,
бойынша реті
деп аталады, ал
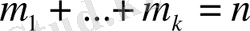 cаны (1)
жүйенің реті
деп аталады.
cаны (1)
жүйенің реті
деп аталады.
Қандай да бір
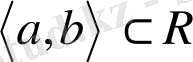 аралығыңда анықталған
аралығыңда анықталған
 функциялар жиынтығы (жүйесі) мына шарттарды:
функциялар жиынтығы (жүйесі) мына шарттарды:
1)
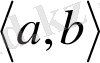 аралығында
аралығында
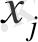 ,
,
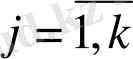 функцияларының сәйкес
функцияларының сәйкес
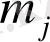 ретке дейінгі туындылары бар;
ретке дейінгі туындылары бар;
2)

3)
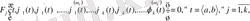
Қанағаттандыратын болса, онда оны 1 жүйенің аралығындағы шешімі деп атайды.
Жүйенің шешімін табу үдерісі оны интегралдау деп аталады.
(1) түрде жазылған теңдеуді қарастыру әр түрлі жағдайларға тәуелді. Солардың негізгілерінің бірі -(1) жүйенің оған кіретін функциялардың ең жоғарғы ретті туындылары бойынша шешілетін жағдайы.
(1) жүйе жоғарғы ретті туындылар
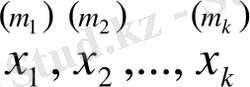 бойынша шешілсін :
бойынша шешілсін :
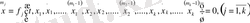 (2)
(2)
Алынған (2) жүйесі к kанондық жүйе деп аталады.
Шешімдерінің арасында өзара сәйкестік бар дифференциаялдық жүйелер эквивалентті деп аталады.
Жоғарға реті теңдеулерден тұратын канондық (2) жүйесі оған эквивалентті, туындылары бойынша шешілетін бірінші ретті теңдеулерден тұратын жүйемен ауыстыруға болоды. Ол үшін (2) жүйеге мынандай ауыстыру енгіземіз:
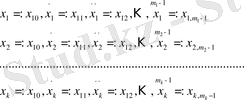
Енгізілген
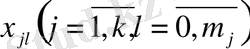 функцияларының жалпы саны
n
-ге тең. Оларға қатысты (2) жүйе мына түрге келтіреді:\
функцияларының жалпы саны
n
-ге тең. Оларға қатысты (2) жүйе мына түрге келтіреді:\
 (4)
(4)
Бұл жүйе
k
топтан құралып тұр. Әрбір
j-
топтағы алғашқы
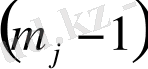 теңдеу
теңдеу
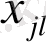 функциялары анықталатын (3) формуладан шығады да, ал соңғы
функциялары анықталатын (3) формуладан шығады да, ал соңғы
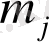 - теңдеуі (2) жүйенің j -теңдеуінен ондағы туындыларды жаңа енгізілген функциялармен ауыстыру арқылы алынады. Сонымен (2) жүйеден (4) алынады. Әлбетте (2) жүйенің әрбір шешімінен (4) жүйенің шешімін табуға болады.
- теңдеуі (2) жүйенің j -теңдеуінен ондағы туындыларды жаңа енгізілген функциялармен ауыстыру арқылы алынады. Сонымен (2) жүйеден (4) алынады. Әлбетте (2) жүйенің әрбір шешімінен (4) жүйенің шешімін табуға болады.
Егер (4) жүйенің әрбір топтың бірінші жолындағы теңдеулер негізінде
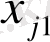 -ді
-ді
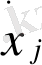 -мен
-мен
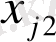 -ні
-ні
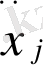 -мен, т. с. с. ,
-мен, т. с. с. ,
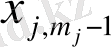 -ді
-ді
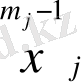 -мен ауыстырып, оларды топтардың соңғы теңдеулеріне қоятын болсақ ( олардағы
-мен ауыстырып, оларды топтардың соңғы теңдеулеріне қоятын болсақ ( олардағы
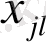 -дің орнына
-дің орнына
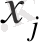 қойып ) , онда әлбетте біз (2) жүйеге қайта ораламыз. Әрине бұл жағдайда (4) жүйенің әрбір шешімінен (2) жүйенің шешімін алуға болады.
қойып ) , онда әлбетте біз (2) жүйеге қайта ораламыз. Әрине бұл жағдайда (4) жүйенің әрбір шешімінен (2) жүйенің шешімін алуға болады.
Ізделінетін функцияларын 1, 2, . . . , n= цифрларымен қайтадан нөмірлесек, яғни
ауыстыруын енгізсек, онда (4) жүйенің туындылар бойынша шешілген бірінші ретті дифференциалдық теңдеулер жүйесінің
(5)
дербес түрі болатынын көреміз. Соңғы жүйені дифференциалдық теңдеулердің қалыпты жүйесі деп атаған болатынбыз. Сол жерде қалыпты жүйе шешімінің және оның түрлерінің (ерекше, дара, жалпы шешімдердің) анықтамалары да берілді.
Канондық (2) жүйенің жеке түрі болып жоғарғы ретті туынды бойынша шешілген n-ретті бір дифференциалдық теңдеу табылады:
(n) (n-1)
.
Бұл теңдеу мынадай қалыпты жүйеге
эквиваленті. Мұндағы айнымалылар
(n-1)
теңдіктері арқылы енгізілген. Сондықтан да бұл теңдеуді n-ретті дифференциалдық теңдеудің қалыпты түрі деп атайды.
2. Эквиваленттік қасиетті пайдаланып, қалыпты жүйені оны жоғарғы ретті біз теңдеуге келтіру арқылы интегралдауға болады. Қалыпты жүйенің реті деп оған кіріп тұрған теңдеулердің саны аталады.
Реті n-ге тең (5) қалыпты жүйенің n-ретті бір дифференциалдық теңдеуге эквивалентті (шешімдерінің арасында өзара сәйкестік бар болуы мағынасында) екенін көрсетелік.
Жүйенің бірінші теңдеуін алып, оны t бойынша дифференциалдайық
Мұндағы -лерді олардың (5) жүйедегі мәндері -лермен ауыстырсақ,
яғни
теңдеуін аламыз. Оны тағы да tбойынша дифференциалдап, (5) жүйені ескере отырып,
Яғни
теңдеуін аламыз. Әрі қарай осылайша жасай беру арқылы мынадай теңдеулерді
(6)
аламыз. Алдыңғы тұрған n-1 теңдеулерден құралған мына жүйе
(7)
айнымалылары бойынша шешілген, яғни одан
(n-1)
өрнектері алынсын. Бұл табылған шамаларының өрнектерін (6) жүйенің соңғы теңдеуіне қойсақ,
(n) (n-1)
(8)
теңдеуі алынады. Бұл - n-ретті дифференциалдық теңдеу. Оның алыну жолынан мынау көрініп тұр: егер (5) жүйенің қандай да бір аралығындағы шешімі болса, онда теңдеудің осы аралығындағы шешімі.
Керісінше, функциясы (8) теңдеудің қандай да бір аралығында шешімі болсын. Оны дифференциалдау арқылы
(n-1)
, мәндерін табамыз. Бұл белгілі
(n-1)
функцияларын (7) жүйеге қоялық. Ұйғарым бойынша ол жүйе айнымалыларына қатысты шешіледі, яғни шамалары t айнымалысының белгілі функциялары ретінде өрнектеліп шығады. Сонда табылған функциялар жиынтығы (5) жүйенің аралығындағы шешімі болады.
Шынында да (7) жүйенің айнымалылары бойынша шешілуі осы айнымалылардың қарастырылып отырған мәндерінде мына якобиан (квадрат Якоби матрицасының анықтауышы)
(9)
нөлге тең емес дегенді білдіреді. Осы (7) жүйеден табылған функциялары мен (8) теңдеудің шешімі болатын функциясын (7) жүйеге қайта қоятын болсақ, тепе-теңдіктер жүйесін аламыз. Бірінші теңдік
,
түрінде, ал екінші теңдік
түрінде болатыны айқын. Бірінші екінші теңдікті алсақ,
,
алынады. Дәл осылайша
,
теңдігі алынады. Әрі қарай жалғастыра отырып, ең соңында
,
теңдігін аламыз. Бұл теңдіктерден бірінші теңдікті ескере отырып мынадай теңдіктер жүйесін аламыз:
Бұл теңдіктерді , белгісіздеріне қатысты сызықтық біртекті жүйе ретінде қарастырамыз. Жүйенің анықтауышы (9) якобианға тең. Ал ол нөлге тең емес. Сондықтан жүйенің жалғыз ғана нөлдік шешімі
бар. Бұларға бірінші теңдікті қосып,
теңдігінің орындалатынын аламыз. Демек, функциялар жиынтығы (5) жүйесінің шешімі болады.
Сонымен, (9) якобиан нөлге тең болмаған кезде, n-ретті (8) теңдеуді шешу арқылы (5) қалыпты жүйені шешуге мүмкіндік туады.
- Қалыпты жүйенің векторлық түрде жазылуы. Қысатын бейнелеу қағидасын қолданып, Коши есебі шешімінің бар және жалғыз болуы туралы теореманы дәлелдеу
Дифференциалдық теңдеулердің қалыпты жүйесі
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz