Жоғары оқу орындарында оқытылатын дифференциалдық теңдеулерді шешудің әр түрлілігін зерттеу

Мазмұны

Кіріспе . . .

Негізгі бөлім

1. сызықтық теңдеулердің жалпы қасиеттері . . .

2. Функцнялардың сытыктық тәуелділігі мен сызықтық тәуелсіздігі . . .

3. сызықтық біртекті теңдеу шешімдерініц қасиеттері . . .

4. Сызықтық біртекті емес теңдеулер . . .

Кіріспе

дифференциалдық теңдеулер курсы студенттердің белгілі бір математикалық мәдениетін немесе олардың ғылыми, әсіресе математиканы оқытудың практикалық және қолданбалы бағыттарының мәнін түсіну, сол сияқты математикалық модельдеудің әдістерін меңгеру мен пәнаралық байланыстарды жүзеге асыру іскерлігі сияқты көзқарастырын қалыптастыру тұрғысынан болсын болашақ мұғалімдердің іргелі математикалық дайындықтарына атқарар ролі аса зор.

Дифференциал дықтең деулер пәні ғылыми зерттеу және қолдан бүны матемикада көптеп пайданылып, бұл пән математикалық анализ, сызықты алгебра .

Тедңеу ұғымы жалпы математикалық ұғымдардың негізгілерінің біріне жатады. Тендеу - айнымалысының ең үлкен дәрежесіне қарай сызықтық теңдеу, квадраттық теңдеу, кубтық теңдеу, т. с. с. Болып бөлінеді.

теңдеу ұғымының тарихына қарасақ вавилондықтар (б. э. д. 2000 жылдар шамасында) теңдеудің кейбір түрлерін: толымсыз квадрат теңдеулерді және толық квадрат теңдеулердің дербес түрлерін 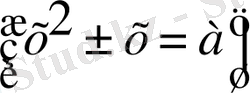шеше білген. Сына тәрізді жазумен жазылѓан есептердің шешуі (рецептер тұрінде) жазылған мәтіндердің табылуы бұған дәлел болады. Ежелгі грек математиктері квадрат теңеулердің кейбір түрлерін шешуді геометриялық салуларѓа келтіріп шеше білген.

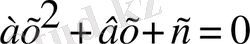
диофант (б. э. д. 3 ѓ. ) Тендеулерді шешудің тәсілдерін геометрияѓа сүйенбей-ақкµрсеткен. Диофант µзініњ ќазірге дейін саќталып келген “арифметика” атты кітабында толыќ квадрат тендеулерді шешу тәілін баяндаѓан. Үнді ғалымы брахмагупта (7 ѓ. ) 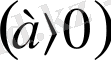түрінекелтірілген квадрат тендеулерді шешу ережесін берген.

хорезм математигі єл-хорезми “китаб єлджебр валь-мукадала” деген трактатында 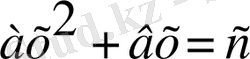, , 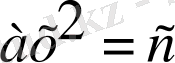, , 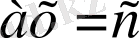, 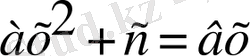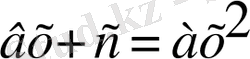түріндегі тендеулерді шешу тәсілдерін түсіндірген және тек оң түбірлер ғана ізделген, ал 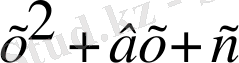түрінекелтірілген квадрат тендеулерді шешудің жалпылама ережесін неміс математигі м. Штифель (1487-1567) тұжырымдады. Жалпылама түріндегі тендеулерді шешу формуласын қорытып шғарумен ф. Виет (1540-1603) айналысты.

Тақырыптың өзектілігі:

Математика курстарын оқытуда оқу процесінде дифференциялдық теңдеулер пәнінде қарастырылатын сызықты дифференциалдық теңдеулер жүйесін интегралдаудың әдістерін қарастыра отырып, математиканы тереңдетіп оқытатын жоғары математиканы өткенде қолдану.

Кустық жұмыстың мақсаты:

Жоғары оқу орындарында оқытылатын дифференциалдық теңдеулерді шешудің әр түрлілігін зерттеу, пәнді оқытуда есептеулерді интегралдап үйрету, математика курсында оқу процесінде пәнаралық байланыстар орнату, теорияда алған білімдерін практикада жүзеге асыру, ұқыптылыққа тәрбиелеу және ойлау қабілеттерін дамыту болып табылады.

Курстық жұмыстың міндеттері:

1. Интегралдап шешудің әр түрлілігін анықтау және есептер шығаруда қолдану.
2. Интегралдау әдістерін жоғары оқу орындарында тереңдетіп оқыту.
3. Интегралдау әдістерін барлық түрлерін арнайы қарастыру арқылы оларды шешудің тиімді әдістемесін жасау.

Негізгі бөлім

Сызықтық теңдеулердің жалпы қасиеттері

Ізделінетін функция мен оның туындылары бойынша сызықтықболатын n -ретті дифференциалдық теңдеу

$${a_{0}(t) x}^{(n) } + a_{1}(t) x^{n - 1} + . . . + a_{n - 1}(t) \dot{x} + a_{n}(t) x = f(x) \ \ \ \ \ \ \ \ \ \ {(1`) }^{`}$$

N-ретті cызықтық дифференциалдық теңдеу деп аталады. Мұндағы $a_{0}(t), a_{1}(t), . . . , a_{n}(t) :\ \ \ : < a, b > \rightarrow$ r функциялары теңдеудің коэффициентері деп, n- бос мүше немесе теңдеудің оң жағы деп аталады. Олар берілген $< a, b >$ b ( аралығында үзіліссіз деп саналады және $\exists t \in < a, b >$ , $a_{0}(t) \neq 0$

(теңдеу n-ретті) . Егер $\ \forall t \in < a, b >$ болса, оңда теңдеудің екі жағын да сол коэффициенткез бөліп, мына теңдеуді

$$x^{(n) } + p_{1}(t) x^{n - 1} + . . . + p_{n - 1}(t) \dot{x} + p_{n}(t) x = f(x) \ \ \ \ \ \ \ \ \ \ (1)$$

Аламыз. Мұнда

$$p_{j}(t) = \frac{a_{j}(t) }{a_{0}(t) } \in C < a, b >, J = \overline{1, n}; \ \ \ q(t) = \ \frac{f(t) }{a_{0}(t) } \in C < a, b > \ \ \ \$$

Егер $\exists t \in < a, b >$ , $f(t) \neq 0$ немесе $q(t) \neq 0\$ бодса, онда (1`) немесе (1) теңдеуді сызықтық біртекті емес немесе оң жағы бар сызықтық теңдеу деп атайды.

Мысалы, 2 тараудың § 4-ның соңында қарастырылган х(n) = $\ f(t)$ теңдеуі - сызықтық біртекті емес теңдеу. Онда $p_{j}(t) = 0J = \overline{1, n}, \forall t \in < a, b > .$ Егер де $\forall t \in < a, b >$ , $f(t) \neq 0 \rightarrow \forall t \in < a, b >$ , $q(t) \neq 0$ бодса оңда

${a_{0}(t) x}^{(n) } + a_{1}(t) x^{n - 1} + . . . + a_{n - 1}(t) \dot{x} + a_{n}(t) x = 0\ \ \$ (2)

Немесе
$$x^{(n) } + p_{1}(t) x^{n - 1} + . . . + p_{n - 1}(t) \dot{x} + p_{n}(t) x = 0\ \ \ \ \ \ \ \ \ \$$

Теңдеуі сызықтық біртекті теңдеу деп аталынады. Коэффициентгері ортақ болган жағдайда (2) (не (21) ) теңдеуді сызықтық біртекті емес (1) (не (г) ) теңдеуге сәйкес кезлетін сызықтық біртекті теңдеу деп аттайды. көбінесе біз (1) және (2) түрдегі сызықтық теңдеулерді карастырамыз.

Сызықтық теңдеудің төмендегідей екі ортақ қасиеті бар.

Тәуелсіз айнымалыны қандай да бір болмасын (a, b) аралығында анықталған, осы аралықта п реткіз дейін үзіліссіз дифференциялданатын және бірінші ретті туындысы нөлгетең емес $\ ѱ(\tau)$ функциясымен $ѱ(\alpha) = a, \ ѱ(\beta) = b$ ауыстырғанда сызықтық теңдеу сызықтық болып қала бередә.

Шынында да (1) теңдеуге $t = \ ѱ(\tau), ѱ: < \alpha, \beta > \ \rightarrow < a, b >$ ауыстыруын енгізелік. Мұнда

$ѱ(\tau) \in C^{n} < \alpha, \beta >, ѱ`(\tau) \neq 0, \forall\tau \in < \alpha, \beta > . $

Онда

$$\dot{x} = \frac{dx}{d\tau} \bullet \frac{1}{\frac{dt}{d\tau}} = \frac{1}{ѱ`(\tau) }x_{\tau}^{`}$$

$$\ddot{x} = \frac{1}{ѱ`(\tau) }\frac{d}{d\tau}\left( \frac{x_{\tau}^{`}}{Ѱ`(\tau) } \right) = \frac{1}{ѱ^{`2}(\tau) }x_{\tau^{2}}^{``} - \frac{Ѱ``(\tau) }{Ѱ^{`3}(\tau) }x^{`}(\tau) $$

. .

бұдан кез келгенк -ретгі $x, 1 \leq k \leq n$ , туындының $x_{\tau}^{`}, x_{\tau^{2}}^{``}, \ldots, x_{\tau^{k}}^{(k) } = :\frac{d^{k}x}{d\tau^{k}}$ арқылы сызықтық өрнектелетінін оңай көруге болады.

Сызыктық өрнектің (комбинацияның) коэффнциенттері (а, b) аралығын-

Да үзіліссіз функциялар. Сонда t -ны жәнех-пен оның табылған туындыларын (1) теңдеуге қойсақ қайтадан сызықтық біртекті емес теңдеу алынады. Егер көрсетілгеы ауыстыруды (2) теңдеуге қолдансақ, онда алынатын теңдеу сызықтық біртекті болады.

2°. Ізделінетін функцияны басқа кез келгенфункциямен сызықтықтүрде ауыстырганда (сызыктық түрлеңдіргенде) сызықтық теңдеу сызықтық болып қала береді. Жаңа функция у -ті

$$x = c(t) y + d(t)$$

Ауыстыруы арқылы енгізейік. Мұнда $c(t), d(t) \in C < a, b >$ және $\ \ c(t) \neq 0, \forall t = < a, b >$ сонда

$$\dot{x} = c(t) \dot{y} + \dot{c}(t) y + \dot{d}(t)$$

$$\ddot{x} = c(t) \ddot{y} + 2\dot{c}(t) \dot{y} + \ddot{c}(t) \ddot{y} + \ddot{d}(t)$$

$$\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots\ldots.$$

$$x^{(n) } = c(t) y^{(n) } + n\dot{c}(t) y^{(n - 1) } + \ldots + c^{(n) }(t) y + d^{(n) }(t)$$

Бұл туындылар мен х -тің манін (1) теңдеуге қойып, алынған теңдеудің екі жағын да $c(t) - ға\$ болсек, тағы да коэффицнеттері меп оң жағы $\ < a, b >$ аралығында үзіліосіз болатын (1) түрдогі сытыктык біртекті емес теңдеу аламыз. Егср (2) тецдеуге

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ x = c(t) y$ (3)

Түрлендіруін енгіссек, қайтадан сызықтық біртекті теңдеу аламыз. Ескезрте кезтетін бір жайт, (3) біртекті ауыстыруы (1) немесе (2) теңдеуін $\ (n - 1) -$ ретті туынды кірмейтін теңдеуге әкезлу үшін жиі қолданылады. шынында да, бұл жағдайда

$$(1) \rightarrow c(t) y^{n} + \left( n\dot{c}(t) + p_{1}(t) c(t) \right) y^{n - 1} + \ldots + \left( c^{(n) }(t) + p_{1}c^{(n - 1) }(t) + \ldots + p_{n}c(t) \right) y = q(t)$$

Сонда $y^{(n - 1) }\$ кіретін мүшені жою үшін $\ c(t)$ функцияңын $n\dot{c}(t) + p_{1}(t) c(t) = 0$ теңдеуінің бір шешімі болатындай етіп алса жеткілікті, яғни

$$c(t) = e^{- \frac{1}{n}\int_{}^{}{p_{1}(t) dt}}$$

Біз $(1) `$ теңдеудегі коэффициент $a_{0}(t)$ нөлге тең болмайтын $< a, b >$ аралығын қараумен шектелдік. Ол $(1) `$ теңдеуді (1) теңдеуге кезлтіру үшін қажет болды. Ал (1) теңдеу үшін коши есебі шешімінің бар және жалғыз болуы туралы теорема дәлелденді (іі-тарау, 4, 2-теорема) . Сол теореманың қайтадан ескез түсірелік.

Теорема. Егeр $p_{j}(t), j = \overline{1, n, \ \ }q(t) \$ функциялары қандай да болмасын бір $< a, b >$ аралығында анықталған және үзіліссіз болса, онда кез келген бастапқы берілгендер $t_{0}, x_{0}, x_{0}^{1}, \ldots, x_{0}^{n - 1}, t_{0} \in < a, b > \$ үшін (1) немесе(2) теңдеудің

$$\varphi\left( t_{0} \right) = x_{0}, \dot{\dot{\varphi}\left( t_{0} \right) = x_{0}^{1}, \ldots, \varphi^{(n - 1) }\left( t_{0} \right) = x_{0}^{(n - 1) }\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) }$$

Шартын қанағаттандыратын жалғыз ғана $x = \varphi(t) \in C < a, b >$ шешімі бар болады және ол шешім $< a, b >$ аралығыныц өн бойында анықталады.

Сызықтық біртекті (2) теңдеу қарастырылсын және(4) бастапқы шарт мына түрде

$$\varphi\left( t_{0} \right) = 0, \dot{\dot{\varphi}\left( t_{0} \right) = 0, \ldots, \varphi^{(n - 1) }\left( t_{0} \right) = 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (5) }$$

Яғни функция мен оның туындыларының бастапқы мәні нөлге тең болсын. Онда (5) шартты нөлдік бастапқы шарт деп атайды. Әлбетте (2), (5) есептің шешімі $\ \varphi(t) = 0, \forall t = < a, b >$ функциясы болады, ол функцияны нөлдік шешімм деп атайды. Теоремада келтірілген шешімнің жалғыздық қасиетінен (2х (5) коши есебінең жалғыз шешімі нөдік шешім болатыны шығады.

Бұл тарауда сызықтық теңдеуледің шешімдерінің қасиеттері, жалпы шешімнің құрылымдық түрі және жалпы шешімді құру жолдары қарастырылады. Сызықтық теңдеудің жалпы шешімін құру барысында негізінен «сызықтық тәуелділік», «сызықтық тәуелсіздік» ұғымдары қолданылады

2. Функцнялардың сытыктық тәуелділігі мен сызықтық тәуелсіздігі

Сыэықтық теңдеулердің жалпы шешімін құру барысында, нақты шешімдермен қатар комплекс мәнді шешімдерді де қарастыруға тура келеді. нақты сандар өсінде жататын $< a, b >$ аралығын комплекс сандар

Жазықтығына көшіретін (яғни $< a, b >$ $\rightarrow$ c

$$x(t) = u(t) + iv(t), \ i = \sqrt{- 1}$$

Функциясын $\ < a, b >$ аралығында анықталған нақты аргументті комплекс мәнді (камплекс) функция деп атайды. Комплекс функция $x(t)$ нақты айнымалы t-ның әрбір мәніне $\ u(t) + iv(t)$ комплекс санын қояды. Нақты $\ u(t)$ және $\ v(t)$ функцңялары сәйкес $\ < a, b >$ комплекс функциясының нақты және жорамал бөліктері деп аталады. Бұны қысқаша былай жазады: $\ u(t) = Re\ v(t), \ v(t) = Im\ x(t)$ . Алгебралыққарапайым амалдардың комплекс функцияларга қолданылуы олардың комплекс сандар үшін қолданылуындай. . Комплекс $\ x(t)$ фуккциясы үшін енгізілетін ұгымдар мен қасиеттері $\ u(t),$ $v(t) \$ нақты функцияларының жұбы үшін енгіэілетін ұгымдар мен олардың қасиеттсрі арқылы анықгалады. Мысалы, $x(t)$ функциясының бір нүктедегі немесе аралықтағы үзіліссіздігі деп $\ u(t) v(t),$ жұбының сәйкес нүктедегі немесе аралықтағы үзіліссіздігі түсініледі. егер $\ u(t) v(t),$ нақты функциялар жұбы $< a, b >$ аралығында диффе- ренциалданяғын болса, онда осы аралыққа $\ x(t)$ комплекс функциясы дифференциалданатын функция деп аталады. Кез келген реттегі туындылар да анықталады. Нақты функция туындысының негізгі қасиеттері комплекс фнкцияның туындысы үшін де дұрыс. Қарастырылып отырған $< a, b > \$ аралығында үзілісіз болатын $x(t) \$ комплекс функциясының алғашқы бейнесі(интеграл) деп $\dot{y}(t) = \ x(t), \forall t = < a, b >$ тепе-теңдігін қанағаттандыртын $\dot{y}(t)$ комплекс функцияын айтады.

Әлбетте

$$\int_{t_{0}}^{t}{x(\tau) d\tau = i\int_{t_{0}}^{t}{u(\tau) d\tau + \int_{t_{0}}^{t}{v(\tau) d\tau, \ t_{0, \ t \in < a, b >$$

Нақты функция интегралының иегіің қасиспері комплекс фуикиияиың ингегралы үшін де дұрыс болғандығы теңдігінен тусінікті.

Мысал регінде $x(t) = e^{(\alpha + i\beta) t}\ \ комплекс\ \$ фуикциясы мен қарастыралық, мұндагы $\mathbf{\alpha}$ және $\beta$ -нақты сандар, t-нақты айиммалы.

Енді

$$e^{(\alpha + i\beta) t} = e^{t\alpha} \bullet e^{it\beta}$$

теңдігін және эйлер* формуласын

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ e^{it\beta} = {{Cos}{\beta t} + isin}{\beta t}$

Пайдаланып, $x(t)$ функциясын диффереициалдайық;

$$\dot{x}(t) = \left( e^{(\alpha + i\beta) t} \right) = \left( e^{t\alpha}\left( {{Cos}{\beta t} + isin}{\beta t} \right) \right) = \left( e^{t\alpha}{Cos}{\beta t} \right) + i\left( e^{t\alpha}{Sin}{\beta t} \right) = \alpha e^{t\alpha}{Cos}{\beta t} - \beta e^{t\alpha}{Sin}{\beta t} + i\left( \alpha e^{t\alpha}{Sin}{\beta t + \beta e^{t\alpha}{Sin}{\beta t}} \right) = (\alpha + i\beta) \left( {{Cos}{\beta t} + isin}{\beta t} \right) e^{t\alpha} = (\alpha + i\beta) e^{(\alpha + i\beta) t}$$

Бұл формулаға сүйенсе отырып,

$$\mathbf{y}\left( \mathbf{t} \right) = \int_{\mathbf{t}_{\mathbf{0}}}^{\mathbf{t}}e^{(\alpha + i\beta) t}\mathbf{d\tau} = \frac{\mathbf{1}}{\alpha + i\beta}\left( e^{(\alpha + i\beta) t} - e^{(\alpha + i\beta) t_{0}} \right)$$

Теңдігін аламыз. Себебі $\dot{y}(t) = \mathbf{y}\left( \mathbf{t} \right)$

Әлбетте: $\left e^{(\alpha + i\beta) t} \right = e^{t\alpha}$

Анықтама. Егер $\varphi_{1}(t), \varphi_{2}(t), \ldots, \varphi_{m}(t) : < a, b >$ $\rightarrow$ c

Функциялары үшін

$$\alpha_{1}\varphi_{1}(t) + \alpha_{2}\varphi_{2}(t) +, \ldots, \alpha_{m}\varphi_{m}(t) = 0, \ t \in < a, b > \ \ \ \ \ \ \ (1)$$

Теңдігін қанағаттандыратын, нөлге бәрі бірдей тең емес $\alpha_{j} \in C$ сандары табылатын болса, онда $\varphi_{1}(t), \varphi_{2}(t), \ldots, \varphi_{m}(t)$ функциалары аралығында комплекс сандар өрісіне қаттысты сызықтық тәуелді деп атталады .

Әдетте

$$Α_{1}E^{\gamma t} + \alpha te^{\gamma t} + \ldots + Α_{m + 1}T^{m}E^{\gamma t} = \left( Α_{1} + Α_{2}t + \ldots + \alpha_{m + 1}T^{m} \right) E^{\gamma t} = 0, \ \forall t \in < a, b > \rightarrow \alpha_{1} + \alpha_{2}t + \ldots + \alpha_{m + 1}t^{m} = 0, t \in < a, b >$$

Себебі $\mathbf{e}^{\mathbf{\gamma t}} \neq \mathbf{0}, t \in < a, b >$ . сондықтан берілген функцияалар сызықтық тәуелсіз.

Мысал. Егср $\gamma_{1}, \gamma_{2} \in C_{0}$ және ${\ \ \gamma}_{1} = \gamma_{2}$ болса, онда

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс