Лопиталь ережесі және тейлор формуласы

Кіріспе...
1 Лопиталь ережелері...
1.1 Қарапайым жағдай..
1.2 Лопиталь ережесі...
1.3 Лопиталь ережесін қолдануға кейбір мысалдар ... ... ... ... ... ... ... ...
1.4 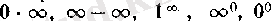түріндегі анықталмағандықты ашу ... ... .
2 Тейлор формуласы.
2.1 Функция және оның түрлері, оларды есептеп шығару теоремалары, Тейлор теоремасы..
2.2 Аралас туындылар туралы теорема, жоғарғы ретті дифференциалдар. Екі айнымалылы функция үшін Тейлор формуласы...
Қорытынды ...
Қолданылған әдебиеттер тізімі...

Жуық формулалар - функцияның мәндерін есептеу үшін жуық формулалар қолданылады. Жуық формулалар алудың негізгі әдісі - функцияны қатарға жіктеу. Көбінесе функция Тейлор қатарына жіктеледі. Функцияның нақты және қатар көмегімен есептелген жуық мәндері арасындағы айырымды бағалау үшін, қатардың толықтауыш мүшесі қарастырылады. Мысалы, жуық формулалар Тейлор қатары арқылы алынса, онда осы қатардың Пеано, Шлемильх және Роша, Лагранж, Коши түріндегі толықтауыш мүшелерінің бірі бағаланады.
Тейлор қатары – функцияны көрсеткішті функциялар шексіз қосындысы ретінде жазу. Тейлор қатарының дербес қосындылары болып Тейлор көпмүшелігі саналады. Рн(х)=ф(х)-Сн(х) Тейлор қатарының қалдық мүшесі, мұндағы Сн(х) – Тейлор қатарының алғашқы н+1 мүшесінің қосындысы. болғанда Тейлор қатары ф(х) функциясына жинақты болады, яғни формуласы шығады. Бұл формуланы 1715 жылы ағылшын математигі Б.Тейлор (1685 – 1731) тапқан, х0=0 болған кезде Маклорен қатары шығады. Осыған сүйене отырып, негізгі элементар функциялардың Тейлор қатарына жіктелуін жазуға болады.
Егер р-ның аталған ойылған маңайында нольге айналмаса және (4)-тің оң жағындағы шек (ақырлы немесе ақырсыз) бар болса, онда (4)-тің сол жағындағы шек бар болып, (4) теңдігі орындалады.
Дәлелдеуі. Әрине, (4) теңдігін біржақты шектер үшін дәлелдесек, болғаны, өйткені онда екі жақты шек үшін де сондай қорытымды айқын түрде жасалады. Ал оң жакты және сол жақты шектер үшін дәлелдеу ұқсас болғандықтан, теореманы сол жағдайлардың тек қана біреуі үшін, мәселен, оң жақты шек үшін дәлелдейміз.

1. Әубәкір С.Б. Жоғары математика. І, ІІ бөлімдер. Алматы 2000 ж.
2. Жантасов Т.Г., Тұрганбаев М.А. Бірнеше айнымалы функциялар. ВКГТУ, 2004 ж.
3. Жаксыгунова Ж.Т. Дифференциалдық теңдеулер тарауы бойыншасеместрлік есептерді орындауға әдістемелік нұсқаулар. ВКГТУ, 2001ж.
4. Жантасов.Т.Г. Қатарлар тақырыбынан әдістемелік нұсқаулар.ВКГТУ,2004ж.
5. Мұсатаева Г.Т., Қоныспаева А.Т. Жоғары математика. ВКГТУ, 2003ж.__
6. Н.Темірғалиев «Математикалық анализ».Алматы т. 1 Мектеп
7. А.Н.Колмоногоров ,А.М.Абрамов «Алгебра мен анализ бастамалары».Алматы.Рауан.1992.
8. Н.Я.Виленкин,О.С. Ивашев-Мусатов,С.И.Шварцбурд «Алгебра и математический анализ».Москва.Просвешение.1983.
9. Н.Я.Виленкин,О.С. Ивашев-Мусатов,С.И.Шварцбурд «Алгебра и математический анализ».Москва.Просвешение.2000.
10. Б.Т.Төлегенов «Математикалық анализдер лекциялар курсы».1-бөлім.Алматы.1973.

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

Курстық жұмыс
Тақырыбы: Лопиталь ережесі және Тейлор формуласы

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... . 3
1 Лопиталь 5
ережелері ... ... ... ... ... ... . ... ... ... ... ... ... ... ... 5
... ... ... ... ... .. 6
1.1 Қарапайым 10
жағдай ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 11
... ... ... ... ... 13
1.2 Лопиталь
ережесі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... 13
... ... ... ... ... ..
1.3 Лопиталь ережесін қолдануға кейбір
мысалдар ... ... ... ... ... ... .. ... .. 18
1.4 түріндегі анықталмағандықты ашу ... ... . 24
2 Тейлор 25
формуласы ... ... ... ... ... ... . ... ... ... ... ... ... ... ... 26
... ... ... ... ... ...
2.1 Функция және оның түрлері, оларды есептеп шығару теоремалары,
Тейлор
теоремасы ... ... ... ... ... ... . ... ... ... ... ... ... ... ...
... .
2.2 Аралас туындылар туралы теорема, жоғарғы ретті
дифференциалдар. Екі айнымалылы функция үшін Тейлор
формуласы ... ... ... ... ... ... . ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .. ... ..
Қорытынды ... ... ... ... ... ... . ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .. ...
Қолданылған әдебиеттер
тізімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
...
Қосымша ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...
... ... ... ... ... ... ... ... .. ... ..

Кіріспе

23-теорема. (Роллья). Егер 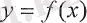функциясы
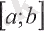кесіндісінде үзіліссіз, осы кесінді ішінде дифференциалданатын және
болса, онда ең кемінде бір 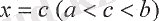нүктесі табылып, 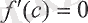теңдігі орындалады.
Лопиталъ ережесі анықталмағандығын ашу үшін). Егер 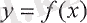және
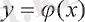функциялары Коши теоремасының шартын нүктесінің қандайда бір
аймағында қанағатандырып, 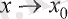болғанда нөлге (немесе ) ұмтылып және
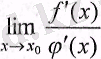шегі бар болса, онда 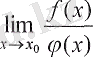шегі бар болады және олар тең болады, яғни

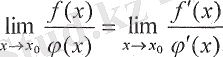
орындалады. Лопиталь ережесі 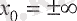болған кезде де орындалады.
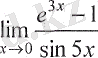Егер 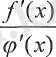қатынасы тағы да екі анықталмағандыктың біреуін берсе
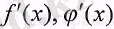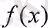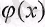және функциялары және функциялары үшін қойылған шарттарды
қанағаттандырса, онда функциялардың екінші туындыларының қатынасына көшуге
болады.
Мысалы, шегін есептеңіз:

Шешуі: Берілген бөлшектің алымындағы және бөліміндегі
функциялар үзіліссіз дифференциалданады және болғанда нөлге ұмтылады.
Сондықтан Лопиталь ережесін қолдануға болады:

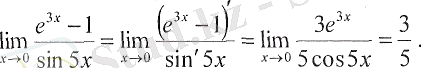
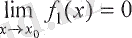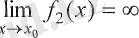Егер және болғанда, түріндегі анықталмағандығы
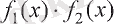көбейтіндісінен алынады. Бұл көбейтіндіні түрлендіру арқылы мына
түрде жазуға болады 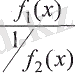немесе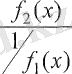, ал бұл бізге немесе
анықталмағандығын береді.
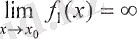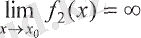Егер де және болса, онда айырмасы
түріндегі анықталмағандық болады. Ал екі функцияның айырмасын мына
түрде жазуға бсшады:

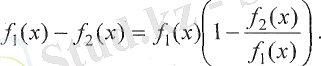
Егер 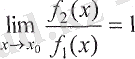болса, онда бұл тендіктен түріндегі анықталмағандығы
алынады.
Мысалы, 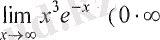түріндегі анықталмағандық) шегін есептеңіз:
Шешуі:

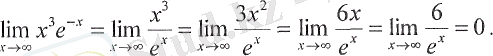
Курстық жұмыстың мақсаты: Лопиталь ережесі және Тейлор формуласын
зерттеу.

1 Лопиталь ережелері

1.1 Қарапайым жағдай

Лопиталь ережелері деп туынды көмегімен анықталмағанлықты ашу тәілдері
аталады.
Шек табу есебі туынды табу есебіне қалай келтірілетінін көрсету үшін
алдымен келесі қарапайым жағдайды қарастырайық.
1 - т е о р е м а. Егер f және 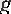функцияларының х0 нүктесінде
туындысы бар болып,

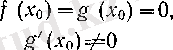(1,2)

шарттары орындалса, онда

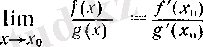(3)

теңдігі орындалады.
Расында да, егер 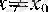болса, опда (1) бойынша

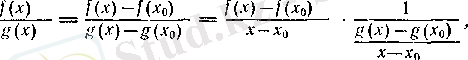
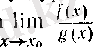демек, х—х0 болғанда (2) және бөлшекте шекке көшу туралы теорема бойынша
(3) теңдігіне келеміз. Бұл жағдайда

шегі түріндегі анықталмағандық болады, өйткені f
және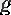функцияларының х0 нүктесінде туындылары бар болғандықтан, олар сол
нүктеде үзіліссіз де болады, демек, (1) бойынша

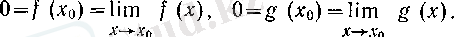
Сөйтіп, 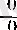түріндегі анықталмағандықты ашу есебі туынды табу есебіне
келтірілді.
Мысалдар. 1. f (x)=x2 — 5x + 6, g (x) = x2-3x + 2 болсын.

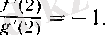Онда хо = 2 үшін (3) бойынша
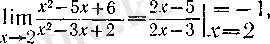
өйткені f'(x)=2x-5, g (x) =2x-3 болғандықтан, Дәл солай,

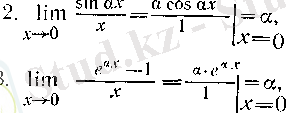
1.2 Лопиталь ережесі

1-теоремада шек табылып тұрған нүкте ақырлы болып, сол нүктеде f және
g функцияларының туындысы бар болса, онда шек табудың жалпы жағдайыи
қарастырайық. Мұнда, біріншіден, шек табылып тұрған нүкте кез келген
(яғни, ақырлы немесе ақырсыз), екіншіден, сол нүктеде f және g
функцияларының қатынасы 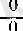немесе түріндегі анықталмағандық
болады, үшіншіден, туынды нүктенің өзінде емес, оның ойылған маңайында
алынады.
Бұл жағдайда Лопиталь ережесі мына түрде жазылады:

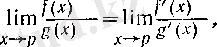(4)

(4) теңдігін былай түсіну керек: егер оң жақтағы шек (ақырлы немесе
ақырсыз) бар болса, онда сол жақтағы шек те бар болып, он жақтағы шекке тең
болады.
Әрине, біз алдымен (4) теңдігінің орындалу шарттарын беруіміз керек.
Ол шарттар (4) -ті мазмұнды ететін шарттардың дәл өзі болады:
2-теорема. f және g функциялары р-ның ойылған маңайында
дифференциалданып, олардың қатынасы р нүктесінде 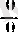немесе
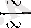түріндегі анықталмағандық болсын, яғни сәйкес

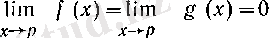(5)

немесе

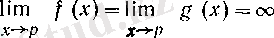(6)

шарттары орындалсын.
Егер р-ның аталған ойылған маңайында 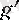нольге айналмаса және (4)-
тің оң жағындағы шек (ақырлы немесе ақырсыз) бар болса, онда (4)-тің сол
жағындағы шек бар болып, (4) теңдігі орындалады.
Дәлелдеуі. Әрине, (4) теңдігін біржақты шектер үшін дәлелдесек,
болғаны, өйткені онда екі жақты шек үшін де сондай қорытымды айқын түрде
жасалады. Ал оң жакты және сол жақты шектер үшін дәлелдеу ұқсас
болғандықтан, теореманы сол жағдайлардың тек қана біреуі үшін, мәселен, оң
жақты шек үшін дәлелдейміз.
Сонымен, (4) теңдігін жоне 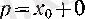(х0 — нақты сан) үшін
дәлелдейік. Егер

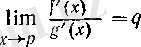(7)

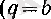нақты caн, 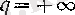немесе) болса, онда келесі алты жағдайдың
біреуі орындалады:

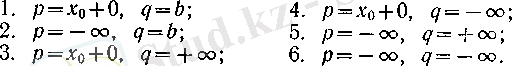
Бұл жағдайлардың әрқайсысы үшін (4) теңдігі келесі екі тұжырымнан
шығады:
а) Егер болса, онда әрбір бойынша болғанда
барлық үшін,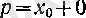" болғанда барлық үшін

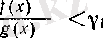(8)

теңсіздігі орындалатын 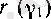саны табылады.
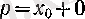б) Егер болса, 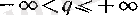онда әрбір бонынша болғанда барлық
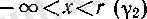үшін, болғанда барлық үшін

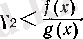(9)

теңсіздігі орындалатын 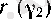саны табылады.
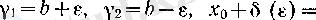
Расында да, 1) жағдайында 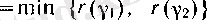болғанда (8) және (9) бойынша
барлық 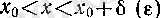үшін 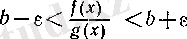болады, яғни 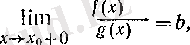демек, 1) жағдайында
(4) орындалады.
Дәл солай, 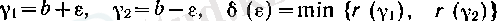деп алып, (4) теңдігінің 2) жағдайында да
орындалатынын көреміз.
Ал 5) жағдайында 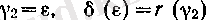болғанда (9) бойынша барлық
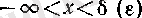
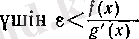болады, яғни

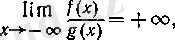
демек, 5) жағдайында да (4) орындалады.
Дәл солай, 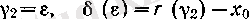деп алып, (4) теңдігі 3) жағдайында да
орындалатынын көреміз.
Соңғы, 4) және 6) жағдайларында да, (4)-тің орындалуы а)-ны қолдану
арқылы дәлелденеді.
Жоғарыдағыдай, а) мен б)-ның дәлелдеуі ұқсас болғандықтан, тек қана а)-
ны дәлелдейміз. Алдымен, мынаны ескерейік: 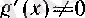болғандықтан, ол р-ның оң
жақты ойылған маңайында бір таңбалы (оң немесе теріс) болады, өйткені х1
және х2 нүктелерінде 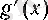функцияларының таңбалары қарама-қарсы
болса, онда Дарбу теоремасы бойынша олардың арасында 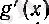функциясы нольге
айналатын нүкте табылар еді. Анықтық үшін 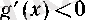болсын. Онда
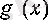кемімелі (5 (§ 3)-п. қараңыз), яғни

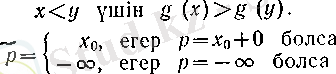(10)

үшін 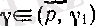болсын, яғни 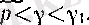Онда (7) бойынша барлық 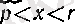үшін

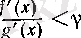(11)

теңсіздігі орындалатын саны табылады. Егер болса, онда Коши
теоремасы мен (10) шарты бойынша

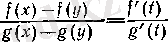
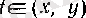саны бар болады, демек, болғандықтан, (11) бойынша

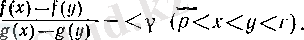(12)

Әуелі а)-ны (5) жағдайында дәлелдейік. (12) теңсіздігінің екі
жағындағы өрнектерді х-ке тәуелді функциялар ретінде қарастырып,
болғанда шекке көшсек, онда әрбір 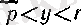үшін (5) бойынша
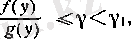яғни 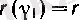үшін а) дәлелденді. Енді а)-ны (6) жағдайында
дәлелдейік. 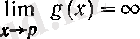болғандықтан, (10) бойынша

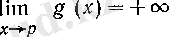(13)

болады. (12) теңсіздігін қанағаттандыратын у сандарының біреуін осы
дәлелдеу аяқталғанша бекітіп алайық. (13) бойынша барлық 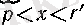үшін
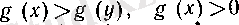теңсіздіктері орындалатын 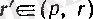саны бар болады. Аталған х сандары үшін
(12) теңсіздігінің екі жағында 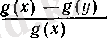оң санына көбейтсек, онда

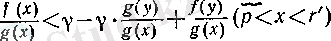
болады.
Мұнан 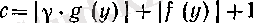үшін

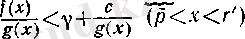(14)

теңсіздігі шығады. (13)-тен 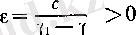бойынша барлық үшін
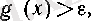яғни

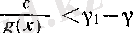(15)

теңсіздігі орындалатып 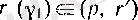саны табылады.
Сонымен, (14) пен (15) бойынша 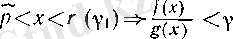болады, яғни бұл жағдайда да
а) дәлелденді.
Теорема толық дәлелденді.
Е с к е р т у. (4)-тің сол жағындағы шек бар болып, оң жағындағы шек
болмауы мүмкін. Мысалы,

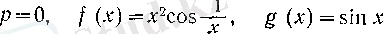болғанда

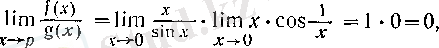
ал 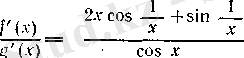функциясының 0 нүктесінде шегі болмайды, өйткені
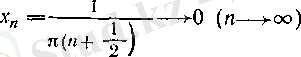үшін

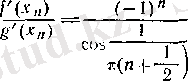
тізбегінің ешқандай шегі жоқ. Ал 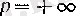болғанда

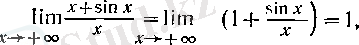
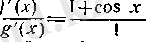бірақ, функциясының 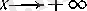болғанда ешқандай шегі жоқ.

Бұл мысалдың мағынасы мынадай: функцияның шегі бар болса да, оны табу
үшін Лопиталь ережесі қолданылмауы мүмкін.

1.3 Лопиталь ережесін қолдануға кейбір мысалдар

Көбінесе Лопиталь ережесі элементар функциялардың шегін табуға
қолданылады, өйткені олардың туындылары оңай және айқын түрде табылады.

1.

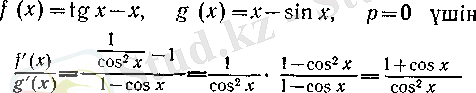
демек, (4) бойынша

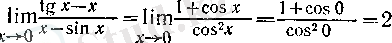
2. Кейде Лопиталь ережесін қайталап қолдануға тура келеді. Лопиталь
ережесінің екі қолдануының арасында алдыңғы қолдануда пайда болған
туындылардың қатынасын әр түрлі жолмен ықшамдап, ортақ көбейткіштерге
қысқартып, бұрыннан белгілі шектерді пайдаланған жөн (бірақ, нәтижесінде
пайда болатын өрнекті 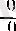немесе 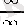түріндегі анықталмағандық ретінде
бейнелеу қажеттігін ұмытпау керек). Мысалы,

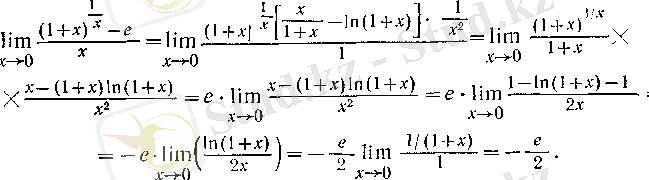
Мұнда Лопиталь ережесі үш рет қолданылған, екінші қолданылуының
алдында 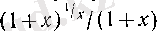көбейткішінің шегі е болатыны ескеріліп, шек таңбасының
алдына е саны жазылған.
3. п — оң бүтін caн, болса, онда

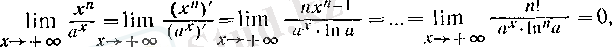
демек, болғанда х-тің әрбір оң дәрежесіне ах көрсеткіштік
функциясына қарағанда жән өседі.
4. а саны оң болса, онда

яғни болғаида In x функциясы х-тің әрбір оң дәрежесіне қарағанда
жәй өседі.

1.4 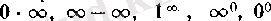түріндегі анықталмағандықты ашу

1°. Егер болса, онда 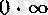түріндегі анықталмағалдық болатын
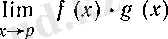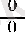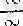шегінің зерттеуі сәйкес және түріндегі анықталмағандық
болатын 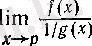және 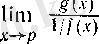шектерін зерттеуге келтіріледі. Мысалы,

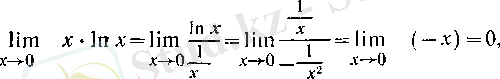
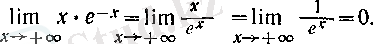
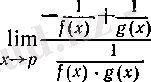2°. Егер 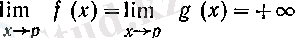болса, онда түріндегі анықталмағандық болатын
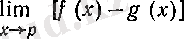шегінің зерттеуі 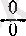түріндегі анықталмағандық болатын

шегін зерттеуге келтіріледі. Мысалы,

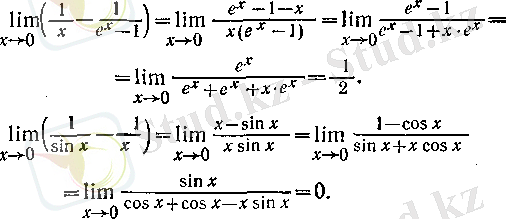
3°.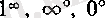түріндегі анықталмағандықтар 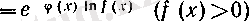түрлендіруі арқылы
түріндегі анықталмағандыққа келтіріледі. Мысалдар:

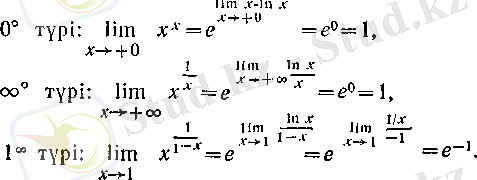
2 Тейлор формуласы

2.1 Функция және оның түрлері, оларды есептеп шығару теоремалары, Тейлор
теоремасы

Дифференциалдық есептеулердің маңызды есептерінің бірі функцияны
зерттеудің жалпы амалдарын қарастыру болып табылады.
у=ƒ(х) функциясы қандай да бір интервалда өспелі (кемімелі) деп
аталады, егер х1х2 үшін ƒ(х1)ƒ(х2) (ƒ(х1)ƒ(х2)) теңсіздігі орындалса,
яғни аргументтің үлкен мәніне функцияның үлкен мәні сәйкес келсе.
Функцияның өсу белгілерін атап өтейік.
1. Егер [а;b] кесіндісінде дифференциалданатын y=ƒ(x) функциясы өспелі
(кемімелі) блса, онда осы кесіндіде функцияның туындысы теріс емес (оң
емес), ягни f΄(x) 0 (f΄ (х)0).
2. Егер [a;b] кесіндісінде үздіксіз және оның ішінде
дифференциалданатын функцияның оң (теріс) туындысы бар болса, онда функция
осы кесіндіде өседі (кемиді).
y=f(x) функциясы қандай да бір интервалда кемімейтін (өспейтін) деп
аталады, егер осы интервалдан алынған кез-келген х1х2 үшін ƒ(х1) ≤ ƒ(x2)
(ƒ(х1) ≥ f(x2)) теңсіздігі орындалса.
Функция кемімейтін немесе өспейтін интервалдар функцияның монотондық
интервалдары деп аталады. Функцияның туындысы нөлге айналатын немесе
үзілетін нүктелері оның кризистік нүктелері деп аталады.
Егер кез-келген Δх≠0 шексіз аз үшін f(x1+Δx)f(x1) теңсіздігі
орындалса, онда х1 нүктесі y=f(x) функциясының локальды максимум нүктесі
деп аталады. Егер кез-келген Δх≠0 шексіз аз үшін f(x2+Δx)ƒ(x2) х2
теңсіздігі орындалса, онда х2 ннүктесі у=f(x) функциясының локальды минимум
нүктесі деп аталады. Максимум және минимум нүктелері функцияның экстремум
нүктелері деп аталады.
Теорема 1 (локальды экстремумның қажетті шарты). Егер y=f(x)
функциясының х=х0 нүктесінде экстремумы бар болса, ондаƒ΄(х0)=0 немесе
f(x0) жоқ.
Теорема 2 (локальды экстремумның бірінші жеткілікті шарты). y=f(x)
функциясы х=х0 нүктесі жататын қандай да бір интервалда үздіксіз және осы
интервалдың барлық нүктелерінде дифференциалдансын. Егер хх0 болғанда
f(x)0, ал хх0 болғанда f(х)0 болса, онда х=х0 нүктесінде у=f(x)
функциясының максимумы бар. Егер де хх0 болғанда f(x)0, ал хх0 болғанда
f(x)0 болса, онда х=х0 нүктесінде y=f(x) функциясының минимумы бар.
Теорема 3 (локальды экстремумның екінші жеткілікті шарты). y=f΄(x)
функциясы екі рет дифференциалдансын және f(х0)=0 болсын. Онда х= х0
нүктесінде функцияның локальды максимумы бар, егер f"(х0)0 және локальды
минимумы бар, егер ƒ"(х0)0 болса.
f"(х0)=0 болса, онда х=х0 нүктесінде экстремум болмауы да мүмкін.
Функцияның дөңестігі және ойыстығы. Иілу нуктелері.
Функция графигінің асимптоталары.
y=f(x) функциясымен берілген қисық (a; b) интервалында дөңес деп
аталады, егер қисықтың барлық нүктелері осы интервалдағы оның кез-келген
жанамасынан жоғары жатпаса және (а;b) интервалында ойыс деп аталады, егер
қисықтың барлық нүктелері осы интервалдағы оның кез-келген жанамасынан
төмен жатпаса.
Қисықтың дөңес бөлігін ойыс бөлігінен бөліп жататын М(х0, f(x0))
нүктесі қисықтың иілу нүктесі деп аталады. М нүктесінде қисықтың жанамасы
бар деп есептеледі.
Теорема (функция графигінің дөңестігінің (ойыстығының) жеткілікті
шарты). Егер (а;b) интервалының барлық нүктелерінде y=f(x) функциясының
екінші туындысы теріс (оң), яғни f"(x)0 (f"(x)0) болса, онда y=f(x)
қисығы осы интервалда дөңес (ойыс).
Иілу нүктесінде функцияның екінші туындысы өзінің таңбасын өзгертеді,
сондықтан ол нөлге айналады немесе жоқ болады.
Теорема (иілу нүктесінің жеткіліктілік белгісі). Егер х=х0 нүктесінде
ƒ"(х0)=0 немесе ƒ"(х0) жоқ болса және осы нүктеден өткенде f"(x) өзінің
таңбасын өзгертсе, онда абсциссасы х=х0 болатын нүкте y=f(x) қисығының иілу
нүктесі.
L түзуі y=f(x) қисығының асимптотасы деп аталады, егер қисықтың М
нүктесінен L түзуіне дейінгі қашықтық М нүктесі шексіздікке ұмтылғанда
нөлге ұмтылса.
Егер х= хi (і=1,...,п) нүктелері бар
болып lim f(x) = ±∞, болса, онда х= хi түзулері у=ƒ(х) қисығының тік
(вертикаль) асимптоталары деп аталады.
Егер

ƒ(х) k= lim—— , b= lim (ƒ(х)-kх),

шектері бар болса, онда

х→∞ х х→∞

y=kx+b түзлері y-f(x) қисығының көлбеу асимптоталары деп аталады. (k=0
болғанда, көлденең (горизонталь) асимптотасы).
Көп айнымалылы функция ұғымы, оның шегі, үздіксіздігі.
Жаратылыстанудың көптеген мәселелерін қарастырғанда, айнымалылар
арасында біреуінің бірнеше айнымалыға тәуелді болатын жағдайлары жиі
кездеседі. Мәселен, қабырғалары х және у болып келген төртбұрыштың ауданы х
және у айнымалыларының мәндері арқылы анықталады, ал қабырғаларының
ұзындықтыры х, у, z - тік параллепипедттің көлемі х, у және z үш тәуелсіз
айнымалылардың мәндеріне байланысты анықталады.
Анықтама 1. Айталық X, Ү және Z - қандай да бір сандық жиындар болсын.
Екі айнымалының функциясы деп, хєХ, уєУ, zєZ болатындай реттелген (х; у; z)
үштігінің f жиынын айтады және әрбір реттелген ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.