Монотонды тізбектер және олардың шектері: негізгі теоремалар, e саны және қолданбалы әдістер


Курстық жұмыс
Тақырыбы: Монотонды тізбектер
Мазмұны
Кіріспе . . .
1 Монотонды тізбектер . . .
1. 1 Монотонды тізбектердің анықтамасы. Негізгі теорема . . .
1. 2 Жинақталатын монотонды тізбектердің кейбір мысалдары . . .
1. 3 е саны . . .
1. 4 е санының бейнелеуі . . .
1. 5 Дәлелденген формуланың салдары . . .
1. 6 Сегменттер ұясы туралы теорема . . .
2 Монотонды тізбек бар және оның шегі . е саны. Тартылатын кесінділер принципі. Коши теоремасы . . .
3 Функцияларды туындыларды пайдаланып зерттеу. Функцияның тұрақтылығы мен монотондылығы Локальдық экстремум. Асимптоталар . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
Қосымша . . .
3
4
4
5
8
11
12
14
16
19
22
23
24
Кіріспе
Анықтама. Егер әрбір n (n= 1, 2, . . . ) үшін
 болса, онда {
х
n
} тізбегін өспелі, ал егер
болса, онда {
х
n
} тізбегін өспелі, ал егер
 болса, онда {
х
n
} тізбегін кемімелі деп атайды.
болса, онда {
х
n
} тізбегін кемімелі деп атайды.
Егер әрбір n (n=1, 2, . . . ) үшін
 болса, онда {
х
n
} тізбегін кемімейтін, ал егер
болса, онда {
х
n
} тізбегін кемімейтін, ал егер
 болса, онда {
х
n
} тізбегін өспейтін тізбек деп атайды.
болса, онда {
х
n
} тізбегін өспейтін тізбек деп атайды.
Бұл тізбектердің әрқайсысын монотонды деп атайды. Өспелі және кемімелі тізбектерді қатаң монотонды деп те атайды.
3-теорема. Кез келген жоғарыдан (төменнен) шенелген өспелі (кемімелі) тізбектің ақырлы шегі бар.
Монотонды және шенелген тізбектің әрқашанда нақты мәнді шегі бар болады, өйткені онда
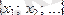 жиынының супремумы мен инфимумы нақты сан болады.
жиынының супремумы мен инфимумы нақты сан болады.
Қатаң монотонды тізбектердің монотонды тізбектерге қарағанда ерекше қасиеттері бар. Мәселен, монотонды тізбектің мәндерінің бәрі де шегіне тең болуы мүмкін (мысалы, x n ≡1 үшін), ал катаң монотонды тізбектің бірде-бір мәні шегіне тең бола алмайды.
Курстық жұмыстың мақсаты: монотонды тізбектерді зерттеу.
Міндеттері:
- монотонды тізбектердің анықтамасын, негізгі теоремасын зерттеу;
- жинақталатын монотонды тізбектердің кейбір мысалдарын қарастыру;
- е саны және е санының бейнелеуін қарастырып өту;
- дәлелденген формуланың салдары мен сегменттер ұясы туралы теореманы зерттеу;
- монотонды тізбек бар және оның шегі, е саны, тартылатын кесінділер принципі және Коши теоремасын зерттеу;
- функцияларды туындыларды пайдаланып зерттеу, функцияның тұрақтылығы мен монотондылығы мен локальдық экстремум және асимптоталарды қарастыру.
1 Монотонды тізбектер
1. 1 Монотонды тізбектердің анықтамасы. Негізгі теорема
Біз тізбектің екі қасиетін - жинақталуын және шенелгендігін - анықтадық. Жинақталатын тізбектің шенелгендігің бірақ шенелген тізбектің жинақталмауы мүмкін екенін көрсеттік. Бір жағдайда осы екі қасиет эквивалентті екен - ол тізбектің монотонды болуы.
А н ы қ т а м а.
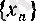 тізбегі берілсін. Егер әрбір
п (п=
1, 2, . . . ) үшін
тізбегі берілсін. Егер әрбір
п (п=
1, 2, . . . ) үшін
 болса, онда оны
кемімейтін
тізбек деп, ал
болса, онда оны
кемімейтін
тізбек деп, ал
 болса, онда оны
өспелі
тізбек деп атайды. Егер әрбір
п
(
п
= 1, 2, . . . ) үшін
болса, онда оны
өспелі
тізбек деп атайды. Егер әрбір
п
(
п
= 1, 2, . . . ) үшін
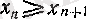 болса, онда оны
өспейтін
тізбек деп, ал
болса, онда оны
өспейтін
тізбек деп, ал
 болса, онда оны
кемімелі
тізбек деп атайды.
болса, онда оны
кемімелі
тізбек деп атайды.
Бұл тізбектердің әрқайсысы монотонды деп аталады. Өспелі және кемімелі тізбектерді қатаң монотонды деп атайды.
Әрине, өспелі тізбек кемімейді, ал кемімелі тізбек өспейді. Сол себептен, кемімейтін және өспейтін тізбектер үшін дәлелденген кез келген тұжырым сәйкес өспелі және кемімелі тізбектер үшін де орындалады. Сонымен бірге, қатаң монотонды тізбектердің монотонды тізбектерге қарағанда ерекше қасиеттері де бар. Мәселен, монотонды тізбектің мәндерінің бәрі де шегіне тең болуы мүмкін (мысалы,
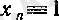 үшін), ал қатаң монотонды тізбектің бірде-бір мәні шегіне тең бола алмайды.
үшін), ал қатаң монотонды тізбектің бірде-бір мәні шегіне тең бола алмайды.
Расында да,
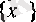 өспелі тізбегі
а
нақты санына ұмтылып, белгілі бір «о үшін
өспелі тізбегі
а
нақты санына ұмтылып, белгілі бір «о үшін
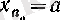 болса, онда барлық
болса, онда барлық
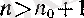 үшін
үшін
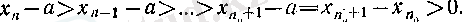
Сөйтіп,
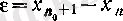 оң саны үшін
оң саны үшін
 болғанда
болғанда
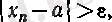 демек,
демек,
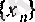 тізбегі
а
санына ұмтылмайды. Қайшылыққа келдік.
тізбегі
а
санына ұмтылмайды. Қайшылыққа келдік.
Монотонды тізбектер бір жақты шенелген болады, өспелі тізбектер-төменнен, кемімелі тізбектер - жоғарыдан (әрқайсысы бірінші мүшесімен шенелген) .
М ы с а л д a p:
1".
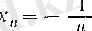 -өспелі шенелген тізбек,
-өспелі шенелген тізбек,
2°. х п = п -өспелі шенелмеген тізбек,
3°. х п = (-1) п • п - шенелмеген, шегі жоқ монотонды емес тізбек.
4°.
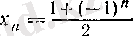 - шенелген, шегі жоқ, монотонды емес тізбек.
- шенелген, шегі жоқ, монотонды емес тізбек.
5°.
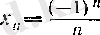 - шенелген, жинақталатын, монотонды емес тізбек.
- шенелген, жинақталатын, монотонды емес тізбек.
Енді монотонды тізбектер туралы негізгі теореманы дәлелдейік.
Т е о р е м а.
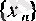 тізбегі монотонды болсын. Онда оның шегі бар (ақырлы әлде ақырсыз) және
тізбегі монотонды болсын. Онда оның шегі бар (ақырлы әлде ақырсыз) және
 кемімейтін болғанда
кемімейтін болғанда
 өспейтін болғанда
өспейтін болғанда
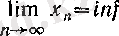 {
х
1
;
х
2
. . .
}.
{
х
1
;
х
2
. . .
}.
Сондықтан, монотонды және шенелген тізбектің әрқашанда нақты мәнді шегі бар болады, өйткені онда
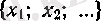 жиынының супремумы мен инфимумы нақты сан болады.
жиынының супремумы мен инфимумы нақты сан болады.
Д ә л е л д е у.
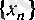 тізбегі кемімейтін болсын. Онда келесі екі жағдайдың біреуі және тек қана біреуі орындалады:
тізбегі кемімейтін болсын. Онда келесі екі жағдайдың біреуі және тек қана біреуі орындалады:
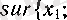
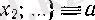 - нақты сан (тізбектің барлық мәндерінің жиыны жоғарыдан шенелген) .
- нақты сан (тізбектің барлық мәндерінің жиыны жоғарыдан шенелген) .
 (тізбектің барлық мәндерінің жиыны жоғарыдан шенелмеген) .
(тізбектің барлық мәндерінің жиыны жоғарыдан шенелмеген) .
1-жағдай. ɛ оң саны берілсін.
Супремумның анықтамасы бойынша:
1)
а
саны
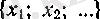 жиынының жоғарғы шекарасы, яғни барлық
п
үшін
жиынының жоғарғы шекарасы, яғни барлық
п
үшін
 болады;
болады;
2)
 саны жиынының
саны жиынының
 жоғарғы шекарасы емес, яғни
жоғарғы шекарасы емес, яғни
 теңсіздігі орындалатын тізбектің
теңсіздігі орындалатын тізбектің
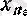 мүшесі табылады.
мүшесі табылады.
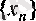 тізбегі кемімейтін болғандықтан
тізбегі кемімейтін болғандықтан
 үшін
үшін
 теңсіздігі орындалады.
теңсіздігі орындалады.
Осының бәрін қорытындылап мынаған келеміз:
Әрбір
 үшін
үшін
 теңсіздігі орындалады, ал бұл жағдай символдар арқылы былай бейнеленеді:
теңсіздігі орындалады, ал бұл жағдай символдар арқылы былай бейнеленеді:
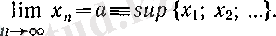
2-жағдай. ɛ оң саны берілсін. Онда ɛ-нан үлкен тізбектің мәні бар болады, яғни
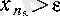 теңсіздігі орындалатын
теңсіздігі орындалатын
 номері табылады.
номері табылады.
Енді тізбектің кемімейтін екенін ескерсек, онда әрбір
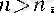 үшін
үшін
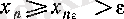 болады, демек, шектің анықтамасы бойынша
болады, демек, шектің анықтамасы бойынша
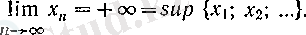 Теорема дәлелденді.
Теорема дәлелденді.
Өспейтін тізбек үшін теорема дәл осылай дәлелденеді.
Е с к е р т у. Дәлелденген теореманың қорытындысын сақтап, шартын сәл жеңілдетуге болады:
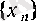 тізбегінің тек қана белгілі бір номерден бастап монотонды болуы талап етіледі, өйткені тізбектің шегіне алғашқы мүшелерінің (қандай да ақырлы жиынын алсақ та) әсері жоқ.
тізбегінің тек қана белгілі бір номерден бастап монотонды болуы талап етіледі, өйткені тізбектің шегіне алғашқы мүшелерінің (қандай да ақырлы жиынын алсақ та) әсері жоқ.
1. 2 Жинақталатын монотонды тізбектердің кейбір мысалдары
Дәлелденген теорема арқылы дөңгелектің ауданын анықтауға болады. Жоғарыда айтылғандай, үшбұрыштың ауданын білсек, онда дөңгелектің ауданын анықтауға болады.
Радиусы 1-ге тең дөңгелекке іштей сызылған 2"-бұрышты көпбұрыштың ауданын
 әрпімен белгілесек, онда
әрпімен белгілесек, онда
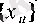 тізбегі өспелі тізбек болатыны айқын.
тізбегі өспелі тізбек болатыны айқын.
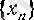 тізбегі шенелген де болады, өйткені әрбір
п
үшін
тізбегі шенелген де болады, өйткені әрбір
п
үшін
 теңсіздігі орындалады. (4-сол дөңгелекке сырттай сызылған квадраттың ауданы) .
теңсіздігі орындалады. (4-сол дөңгелекке сырттай сызылған квадраттың ауданы) .
Демек, дәлелденген теорема бойынша
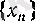 тізбегінің нақты мәнді шегі бар болады, сол caн радиусы 1-ге тең дөңгелектің ауданы деп аталады да
тізбегінің нақты мәнді шегі бар болады, сол caн радиусы 1-ге тең дөңгелектің ауданы деп аталады да
 әрпімен белгіленеді.
әрпімен белгіленеді.
Сонымен, жаңа сан -
 саны - анықталады.
саны - анықталады.
 саны иррационал сан болады, ондық бөлшек арқылы түрлендіруінің алғашқы бес таңбасы мынадай: π = 3, 14159 . . .
саны иррационал сан болады, ондық бөлшек арқылы түрлендіруінің алғашқы бес таңбасы мынадай: π = 3, 14159 . . .
Монотонды тізбектер туралы теорема тізбектің шегі бар болып, мәндерінің жиынының супремумы немесе инфимумына тең болатынын тұжырымдайды. Ал жиынның супремумы мен инфимумын тек қана кейбір қарапайым жағдайларда ғана дәл табуға болады. Сондықтан, негізгі теореманың монотонды тізбектің шегінің мәнін табуға пайдасы аз деуге болады (шектің бар болуы мен оның мәнін дәл табу - өзара бөлек мәселелер! Бұл жалпы факт) . Бірақ кейбір жағдайларда шектің мәнін табуға оның бар болуы туралы мәлімет те жеткілікті. Айтқанымызды мысалдар арқылы түсіндірейік.
1
0
. с>0 үшін
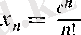 тізбегін қарастырайық. Егер
тізбегін қарастырайық. Егер
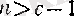 болса, онда
болса, онда
 , демек,
, демек,
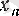 -кемімелі тізбек, ал
-кемімелі тізбек, ал
 болғандықтан, ол төменнен шенелген де болады. Сондықтан
болғандықтан, ол төменнен шенелген де болады. Сондықтан
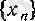 тізбегінің нақты мәнді шегі бар, оны
а
әрпімен белгілейік.
тізбегінің нақты мәнді шегі бар, оны
а
әрпімен белгілейік.
Әрине,
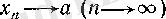 болғандықтан
болғандықтан
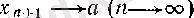
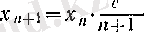
теңдеуі
 тізбегі
тізбегі
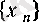 және
және
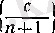 тізбектерінің көбейтіндісі болатынын керсетеді.
тізбектерінің көбейтіндісі болатынын керсетеді.
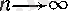 болғанда, шекке көшсек, онда
а = а*0
теңдігіне келеміз, яғни
а = 0.
болғанда, шекке көшсек, онда
а = а*0
теңдігіне келеміз, яғни
а = 0.
Сонымен,
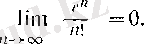
2°. а және х 1 оң сандары берілсін. Мына
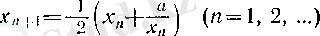 (1)
(1)
рекуррентті формуласы арқылы анықталған тізбектің шегі бар болып,
 санына тең екенін көрсетейік.
санына тең екенін көрсетейік.
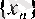 Алдымен тізбегінің төменнен 0 санымен шенелгенін дәлелдейік.
Алдымен тізбегінің төменнен 0 санымен шенелгенін дәлелдейік.
Расында да, берілуі бойынша х 1 oң, caн. Енді х п оң caн деп ұйғарсақ, онда (1) теңдігінен х п+1 -де оң болатыны айқын.
Демек, математикалық индукция әдісі бойынша әрбір п үшін х п >0 болатыны дәлелденді.
Енді
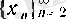 тізбегінің кемімелі болатынын дәлелдейік. (1) теңдігін
тізбегінің кемімелі болатынын дәлелдейік. (1) теңдігін
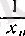 санына көбейтсек (х
п
оң caн!), онда
санына көбейтсек (х
п
оң caн!), онда
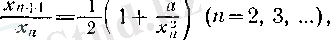
болады, демек,
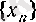 тізбегінің кемімелі болуы
тізбегінің кемімелі болуы
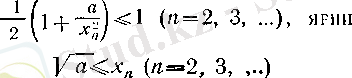 (2)
(2)
теңсіздігіне пара-пар.
(2) теңсіздігін дәлелдеудің алдында әрбір t оң саны үшін
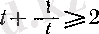 (3) .
(3) .
болатынын көрсетейік.
 болғандықтан,
болғандықтан,
 болады, Соңғы теңсіздіктің екі жағын да
болады, Соңғы теңсіздіктің екі жағын да
 оң санына көбейтіп (3) тедсіздігіне келеміз. (1) теңдігін
оң санына көбейтіп (3) тедсіздігіне келеміз. (1) теңдігін
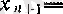
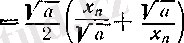 түрінде жазып, жақшаның ішіндегі қосындыға
түрінде жазып, жақшаның ішіндегі қосындыға
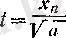 болғандағы (3) теңсіздігін қолдансақ, онда (2) теңсіздігінің орындалатынын көреміз.
болғандағы (3) теңсіздігін қолдансақ, онда (2) теңсіздігінің орындалатынын көреміз.
Сөйтіп,
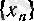 кемімелі тізбек екені дәлелденді кемімелі
кемімелі тізбек екені дәлелденді кемімелі
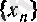 және шенелген тізбек болғандықтан, оның нақты мәнді шегі бар. Ол
а
саны болсын. (1) және (2) -де
және шенелген тізбек болғандықтан, оның нақты мәнді шегі бар. Ол
а
саны болсын. (1) және (2) -де
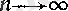 болғанда шекке көшсек, онда сәйкес
болғанда шекке көшсек, онда сәйкес
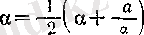 (4)
(4)
және
 (5)
(5)
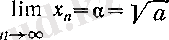
болады. Мұнан біздің мақсатымыз болатын
теңдігі шығады, өйткені (5) шартын қанағаттандыратын (4) -тің түбірі тек қана
 саны болады.
саны болады.
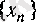 тізбегі
а
-ның квадраттық түбірін жуықтап табу үшін қолданылады.
тізбегі
а
-ның квадраттық түбірін жуықтап табу үшін қолданылады.
Енді
а
оң санының квадраттық түбірін жуықтап есептегенде (1) формуласымен пайдаланып
х
п
-нен
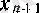 -ге көшкенде сәйкес қателіктердің қалай өзгеретінін қарастырайық.
-ге көшкенде сәйкес қателіктердің қалай өзгеретінін қарастырайық.

теңсіздігі шығады, яғни жаңа
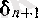 қателігі
қателігі
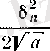 -дан аспайды. Сонымен, әрбір келесі қадамдағы қателік шамамен алдындағы қадамдағы қателіктің квадратына тең болады. Демек, біз
-дан аспайды. Сонымен, әрбір келесі қадамдағы қателік шамамен алдындағы қадамдағы қателіктің квадратына тең болады. Демек, біз
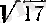 санын, мысалы, үтірден кейін 5 таңбасымен тапсақ келесі қадам дәлдікті 10 таңбаға дейін, ал одан кейінгі қадам 20 таңбаға дейін көтереді. Сондықтан, (1) тізбегі оң саннан квадраттық түбір табу үшін қазіргі есептеу математикасында кеңінен қолданылады.
санын, мысалы, үтірден кейін 5 таңбасымен тапсақ келесі қадам дәлдікті 10 таңбаға дейін, ал одан кейінгі қадам 20 таңбаға дейін көтереді. Сондықтан, (1) тізбегі оң саннан квадраттық түбір табу үшін қазіргі есептеу математикасында кеңінен қолданылады.
1. 3 е саны
Бұл пунктте анализдегі айрықша сандардың бірі - е санын анықтаймыз. Әрбір оң бүтін п үшін
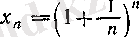 (6)
(6)
болсын. Монотонды тізбектер туралы негізгі теореманы қолданып,
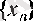 тізбегінің нақты мәнді шегі бар болатынын дәлелдейік.
тізбегінің нақты мәнді шегі бар болатынын дәлелдейік.
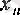 өрнегіндегі
п
дәреже көрсеткіші өскен сайын дәреже негізі кеми түседі, сондықтан,
х
п
монотонды болатыны тікелей көрінбейді.
өрнегіндегі
п
дәреже көрсеткіші өскен сайын дәреже негізі кеми түседі, сондықтан,
х
п
монотонды болатыны тікелей көрінбейді.
Бұны дәлелдеу үшін, х п -ді Ныотон биномы формуласы бойынша жіктейік:

Соңғы қосындының түрінің өзінен-ақ
х
п
өспелі тізбек болатыны оңай шығады. Расында да,
х
п
-
нен
х
п+1
-ге көшкенде, біріншіден, жаңа
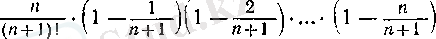 оң мүшесі пайда болады, екіншіден, бұрыннан жазылған
оң мүшесі пайда болады, екіншіден, бұрыннан жазылған
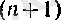 мүшенің алғашқы екеуі өзгермейді де (олар 1 санына тең), ал қалғандарының әрқайсысының орнына одан үлкен өрнек жазылады, өйткені
мүшенің алғашқы екеуі өзгермейді де (олар 1 санына тең), ал қалғандарының әрқайсысының орнына одан үлкен өрнек жазылады, өйткені
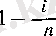 түріндегі әрбір көбейткіш одан үлкен
түріндегі әрбір көбейткіш одан үлкен
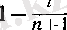 көбейткішіне алмасады. Сонымен, әрбір
п
үшін
х
п
көбейткішіне алмасады. Сонымен, әрбір
п
үшін
х
п
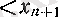 болады, яғни
болады, яғни
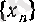 - өспелі тізбек.
- өспелі тізбек.
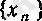 - шенелген тізбек болатынын дәлелдеу үшін, басқа жағдайларда да жиі қолданылатын, келесі формуланы дәлелдейік.
- шенелген тізбек болатынын дәлелдеу үшін, басқа жағдайларда да жиі қолданылатын, келесі формуланы дәлелдейік.
Егер
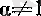 болса, онда әрбір оң бүтін
п
саны үшін
болса, онда әрбір оң бүтін
п
саны үшін
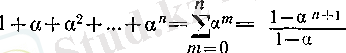 (8)
(8)
теңдігі орындалады. Расында да,
(l - a ) (l+ a + a 2 + . . . + a п ) = (l + a + a 2 + . . . + a п ) - ( a + a 2 + . . . + a п+l ) = 1+ ( а + а 2 + . . . + a п ) - ( a + a 2 + . . . + a п ) - a п+l ,
яғни, (8) дәлелденді.
(7) өрнегіндегі жақшаның ішіндегі әрбір көбейткіш 1 санынан кіші, сондықтан, олардың әрқайсысының орнына 1 санын жазсақ, онда
.
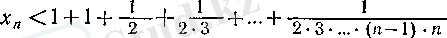 " (9)
" (9)
 теңсіздігіне келеміз. Бұнда әрбір бөлшектің бөліміндегі әрбір көбейткішті 2 санына алмастырсақ, онда
теңсіздігіне келеміз. Бұнда әрбір бөлшектің бөліміндегі әрбір көбейткішті 2 санына алмастырсақ, онда
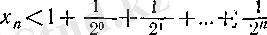 болады. Соңғы теңсіздіктің оң жағындағы қосындыға
болады. Соңғы теңсіздіктің оң жағындағы қосындыға
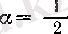 болғандағы (8) формуласын қолдансақ, онда
болғандағы (8) формуласын қолдансақ, онда
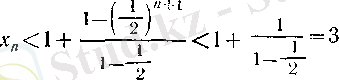
болады, яғни
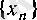 -жоғарыдан шенелген тізбек.
-жоғарыдан шенелген тізбек.
Сөйтіп,
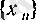 - өспелі және шенелген тізбек болатыны дәлелденді.
- өспелі және шенелген тізбек болатыны дәлелденді.
Сопдықтан, монотонды тізбектің шегі бар болуы туралы теорема бойынша
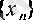 тізбегінің нақты мәнді шегі бар болады. Ол санды Л. Эйлер белгілегендей әрдайым
е
әріпімен белгіленді.
тізбегінің нақты мәнді шегі бар болады. Ол санды Л. Эйлер белгілегендей әрдайым
е
әріпімен белгіленді.
Сонымен,
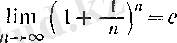 (10)
(10)
е
әріпі жаңа санның белгілеуі екеніне оқырманның назарын тағы да аударамыз: алдымен (6) бойынша анықталған
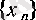 тізбегінің шегі бар және нақты сан болатынын дәлелдедік, сонан кейін сол нақты сан
е
әрпімен белгіленеді.
тізбегінің шегі бар және нақты сан болатынын дәлелдедік, сонан кейін сол нақты сан
е
әрпімен белгіленеді.
Бұл санның ондық бөлшек арқылы түрлендіруінің алғашқы үш таңбасы мынадай болады.
е = 2, 718 . . .
е санын логарифмнің негізі ретінде алған көп жағдайларда өте пайдалы болады (мысалы, 1 (V тарау, § 2) -пункттегі 3°-ті, 4°-ті қараңыз) . Сондай логарифмдер In символымен белгіленеді. Сонымен,
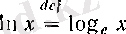
Соңында, әрбір оң бүтін п саны үшін
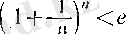 (11)
(11)
болатынын атап өтейік.
Е с к е р т у. (10) теңдігін анықталмағандықты ашу деп қарастыруға болады.
Расында да, .
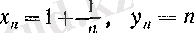 болса, онда
болса, онда
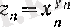 ,
,
 болады, демек, 5 (§ 2) -пункттегі анықталмағандықтың белгілеулеріне сай жазсақ, 1°° символына келеміз. Бұл анықталмағандықты былай түсіндіруге болады: егер
болады, демек, 5 (§ 2) -пункттегі анықталмағандықтың белгілеулеріне сай жазсақ, 1°° символына келеміз. Бұл анықталмағандықты былай түсіндіруге болады: егер
 болса, онда
болса, онда
 үшін
үшін
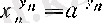
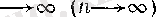 , ал
, ал
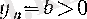 болса, онда
болса, онда
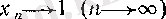 үшін
үшін
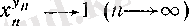 болады.
болады.
Жалпы жағдайда
 өрнегінің «негізі 1-ге тартады», «көрсеткіші
өрнегінің «негізі 1-ге тартады», «көрсеткіші
 -ке тартады», сондықтан, берілген
-ке тартады», сондықтан, берілген
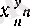 тізбегінің шегі бар болуы, бар болса оның мәні -
х
n
- нің 1-ге,
тізбегінің шегі бар болуы, бар болса оның мәні -
х
n
- нің 1-ге,
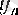 -нің
-нің
 ке ұмтылу тәртіптері мен олардың арасындағы ара-қатынасымен байланысты.
ке ұмтылу тәртіптері мен олардың арасындағы ара-қатынасымен байланысты.
Сондықтан, (10) теңдігін
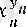 өрнегінде
өрнегінде
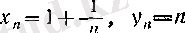 болғанда, олар «бір-бірін өзімен бірге ілестіре кете алмай
болғанда, олар «бір-бірін өзімен бірге ілестіре кете алмай
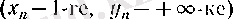 , 1 мен
, 1 мен
 арасындағы бір санға (
е
= 2, 718 . . . деп аталатын) «келіскендері» деуге болады.
арасындағы бір санға (
е
= 2, 718 . . . деп аталатын) «келіскендері» деуге болады.
1. 4 е санының бейнелеуі
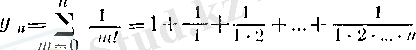 (12)
(12)
болсын (бұл (9) теңсіздігінің оң жағындағы өрнек) . Мұнда
 үшін
үшін
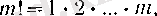 ал келісім бойынша
ал келісім бойынша

Әрбір oң бүтін п үшін
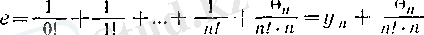 (13)
(13)
теңдігін қанағаттандыратын
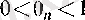 саны табылатынын көрсетейік.
саны табылатынын көрсетейік.
Алдымен,
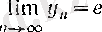 (14)
(14)
теңдігін дәлелдейік (кейбірде
е
саны
 тізбегінің шегі ретінде анықталады) .
тізбегінің шегі ретінде анықталады) .
- оң бүтін саны берілсін. Онда әрбірүшін (7) бойынша
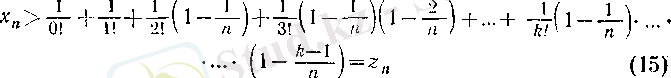
болады.
 болғанда
болғанда
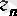 -нің әрбір жақшасындағы өрнектің шегі бар және 1 санына тең болады, демек,
-нің әрбір жақшасындағы өрнектің шегі бар және 1 санына тең болады, демек,
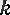 +1 қосылғыш үшін қолданылған 4 (§ 2) -п. 7-теоремасының салдары бойынша
+1 қосылғыш үшін қолданылған 4 (§ 2) -п. 7-теоремасының салдары бойынша
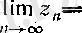 у
Ʀ
теңдігі орындалады. Сондықтан, (15), (10) және 3 (§ 2) -пункттегі 5-теорема бойынша
у
Ʀ
теңдігі орындалады. Сондықтан, (15), (10) және 3 (§ 2) -пункттегі 5-теорема бойынша
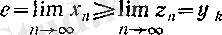 болады.
болады.
Бұдан және (12) анықтамасы мен (9) теңсіздігінен әрбір оң бүтін
п
үшін
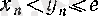 болатынын көреміз, сондықтан, (10) және 3 (§ 2) -п. 6-теорема бойынша (14) теңдігі орындалады,
болатынын көреміз, сондықтан, (10) және 3 (§ 2) -п. 6-теорема бойынша (14) теңдігі орындалады,
Кез келген оң бүтін п және т сандары үшін
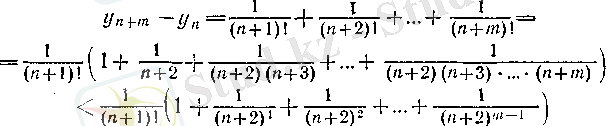
болады, демек,
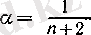 болғандағы (8) формуласы бойынша
болғандағы (8) формуласы бойынша
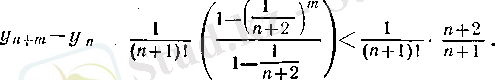
Бұл теңсіздіктің екі жағын да m-ге тәуелді тізбек деп қарастырып, шекке көшсек, онда 3 (§ 2) -пункттегі 5-теорема және (14) теңдігі бойынша
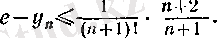
Біз мұнда, әрине, m-ге тәуелді тізбектің мәндерінің бәрі белгілі бір санға тең болса, онда шегі де сол санға тең болатынын пайдаландық.
Әрбір
п
үшін
 және
және
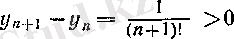 болғандықтан,
болғандықтан,
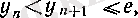 яғни
яғни
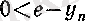 теңдігі орындалады. Сонымен,
теңдігі орындалады. Сонымен,
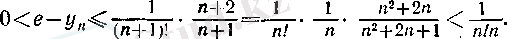
Сондықтан,
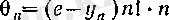 деп алсақ, соңғы теңсіздік (13) формуласының басқа түрде жазылуы болады. (13) формуласы дәлелденді.
деп алсақ, соңғы теңсіздік (13) формуласының басқа түрде жазылуы болады. (13) формуласы дәлелденді.
Ескерту. (13) теңдігі ілгеріде дәлелденетін жалпы формуланың (дәл айтқанда, Тейлор формуласының) дербес жағдайы болады. Бірақ, дәлелдеуі тура (тек қана е саны мен шектің анықтамаларына сүйенетін) және шектің анықтамасы қалай қолданылатынын көрсететін өте пайдалы жаттығу болғандықтан, осы жерде келтірдік.
1. 5 Дәлелденген формуланың салдары
Бұнда (13) формуласының , екі салдарын келтіреміз.
(13) формуланың теориялық мағынасы бар:
е
-нің иррационал caн екенін дәлелдеуге болады. Кері жорып,
е
рационал сан десек, онда белгілі бір
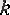 және
т
оң бүтін сандары үшін
және
т
оң бүтін сандары үшін
 болады. Демек,
п = т
үшін (13) былай жазылады
болады. Демек,
п = т
үшін (13) былай жазылады
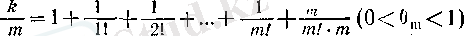
Мұның екі жағын да
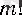 санына көбейтсек, онда теңдеудің сол жағында бүтін сан, ал оң жағында бүтін caн мен
санына көбейтсек, онда теңдеудің сол жағында бүтін сан, ал оң жағында бүтін caн мен
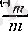 бөлшегінің қосындысы болады, бірақ олай болуы мүмкін емес. Сондықтан, қайшылыққа келеміз, яғни
е
саны иррационал болатыны дәлелденді.
бөлшегінің қосындысы болады, бірақ олай болуы мүмкін емес. Сондықтан, қайшылыққа келеміз, яғни
е
саны иррационал болатыны дәлелденді.
Енді е санын кез келген дәлдікпен табуға болатынын көрсетейік. Расында да, (13) формуласы бойынша әрбір ɛ оң саны арқылы барлық
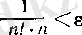 (16)
(16)
теңсіздігін қанағаттандыратын n-дер үшін
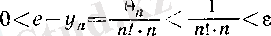 (17)
(17)
теңсіздіктері орындалады. Ал
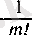 түріндегі рационал санының мәнін есептеу жұмысы қанағаттандырарлықтай деп санасақ, онда (16) мен (17) теңсіздіктері мақсатымызға жеткенімізді көрсетеді. Мысалы,
түріндегі рационал санының мәнін есептеу жұмысы қанағаттандырарлықтай деп санасақ, онда (16) мен (17) теңсіздіктері мақсатымызға жеткенімізді көрсетеді. Мысалы,
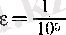 үшін (16) теңсіздігінің ең кіші шешімі (у
n
-нің есептеуі үнемді болуы үшін!) n = 5 болады, демек,
үшін (16) теңсіздігінің ең кіші шешімі (у
n
-нің есептеуі үнемді болуы үшін!) n = 5 болады, демек,
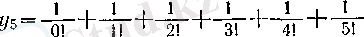 (18)
(18)
рационал санының
е
санынан айырмашылығы
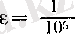 санынан кіші болады.
санынан кіші болады.
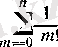 қосындыларының мәні электронды-есептеуіш машиналарында оңай табылады.
қосындыларының мәні электронды-есептеуіш машиналарында оңай табылады.
Ескерту. (13) формуласын былай талқылауға болады. Мәнін дәл білуге болмайтын сан (
е
саны) мәні белгілі мағынада оңай табылатын өрнекпен
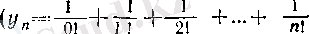 қосындысымен) жуықталады және сонда пайда болатын қателікті қалағаныңызша аз қыла аламыз ((16) . теңсіздігі) .
қосындысымен) жуықталады және сонда пайда болатын қателікті қалағаныңызша аз қыла аламыз ((16) . теңсіздігі) .
Жалпы, құрылысы күрделі затты (мысалы, санды, функцияны, т. б. ) осылай белгілі бір мағынада қанағаттандырарлықтай затпен жуықтау және сонда пайда болатын қателікті қалағанымызша белгілі мағынада аз ете алу - математикада жиі кездесетін жағдай.
Біз ілгеріде кездескен сайын оны ескертіп отырамыз.
1. 6 Сегменттер ұясы туралы теорема
Монотонды тізбектің шегі бар болатыны туралы теорема кейбірде мынадай түрде қолданылады:
Теорема. Егер кемімейтін
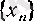 және еспейтін
және еспейтін
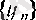 тізбектері үшін
тізбектері үшін
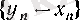 тізбегінің мүшелері оң болып (яғни, әрбір
п
үшін
тізбегінің мүшелері оң болып (яғни, әрбір
п
үшін
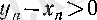 болса), өзі нольге ұмтылса, онда
болса), өзі нольге ұмтылса, онда
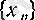 және
және
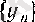 тізбектердің шектері өзара тең болады:
тізбектердің шектері өзара тең болады:
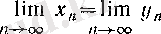 (19)
(19)
Д ә л е л д е у і. Алдымен
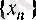 тізбегінің нақты монді шегі бар болатынын дәлелдейік. Әрбір
п
үшін
тізбегінің нақты монді шегі бар болатынын дәлелдейік. Әрбір
п
үшін
 болғандықтан
болғандықтан
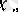
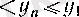 болады, демек,
болады, демек,
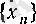 - жоғарыдан шенелген тізбек.
- жоғарыдан шенелген тізбек.
Сондықтан, теореманың шарты бойынша ол кемімейтіндігін ескерсек, онда тізбегінің нақты мәнді шегі бар болатыны дәлелденді.
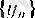 тізбегінің нақты мәнді шегі бар болатыны да дәл осылай дәлелденеді.
тізбегінің нақты мәнді шегі бар болатыны да дәл осылай дәлелденеді.
Сөйтіп 4 (§ 2) -п. 7-теорема бойынша
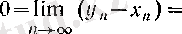
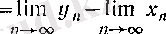 болады, яғни (19) теңдігі, сонымен бірге теорема да дәлелденді.
болады, яғни (19) теңдігі, сонымен бірге теорема да дәлелденді.
Бұл теорема кейбірде басқа, «геометриялық» түрде қолданылады. Оны келтіру үшін бізге келесі анықтамалар қажет. Егер әрбір
п
оң бүтін саны үшін белгілі бір тәртіп бойынша
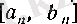 сегменті сәйкес қойылса, онда
сегменті сәйкес қойылса, онда
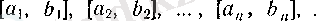 (20)
(20)
сегменттер тізбегі берілді дейді.
Егер бұнда кез келген сегмент алдыңғы сегменттің жиыншасы болып, сегменттердің ұзындықтары нольге ұмтылса, онда (20) -ны сегменттер ұясы деп атайды.
Әрине, (20) сегменттер тізбегі сегменттер ұясы болуы үшін сегменттердің шеткі нүктелерінен құрылған
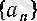 және
және
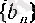 сандар тізбектері келесі екі шарттың
сандар тізбектері келесі екі шарттың
1) әрбір
п
үшін
 яғни
яғни
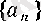 -кемімейтін, ал
-кемімейтін, ал
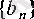 - өспейтін тізбек болуы,
- өспейтін тізбек болуы,
2)
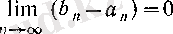 теңдігі орындалуы қажетті және жеткілікті.
теңдігі орындалуы қажетті және жеткілікті.
Сонда дәлелденген теорема былай айтылады:
Сегменттер ұясы туралы теорема.

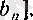 . . .
сегменттер ұясы берілсін. Онда осы сегменттердің әрқайсысында жататын нүкте (нақты сан) бар және жалғыз болады. Ол нүкте сол сегменттердің шеткі нүктелерінен құрылған {
а
n
}және {b
n
}тізбектерінің шектерінің ортақ мәні болады.
. . .
сегменттер ұясы берілсін. Онда осы сегменттердің әрқайсысында жататын нүкте (нақты сан) бар және жалғыз болады. Ол нүкте сол сегменттердің шеткі нүктелерінен құрылған {
а
n
}және {b
n
}тізбектерінің шектерінің ортақ мәні болады.
Расында да, {
а
n
}және {b
n
} тізбектері үшін дәлелденген теореманың шарттары орындалады, демек, сол теорема бойынша
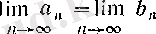 болады. Осы екі шектің ортақ мәнін а әрпімен белгілесек, онда
болады. Осы екі шектің ортақ мәнін а әрпімен белгілесек, онда
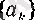 мен
мен
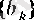 монотонды болғандықтан 1-пункттегі теорема бойынша әрбір оң бүтін
монотонды болғандықтан 1-пункттегі теорема бойынша әрбір оң бүтін
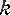 саны үшін
саны үшін
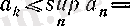
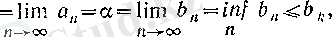 яғни барлық сегменттерде жататын
а
саны бар болатынын көрсеттік.
яғни барлық сегменттерде жататын
а
саны бар болатынын көрсеттік.
Басқа
а
1
саны да осындай болса, онда әрбір
п
үшін

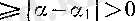 теңсіздігі орындалады, сондықтан, сегменттердің ұзындықтары нольге ұмтыла алмас еді.
теңсіздігі орындалады, сондықтан, сегменттердің ұзындықтары нольге ұмтыла алмас еді.
Ескерту. Бұл теоремада сегменттерді интервалдарға ауыстыруға болмайды. Мысалы,
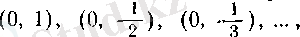
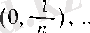 интервалдар тізбегі үшін теореманың шарттары орындалса да, олардың бәрінде жататын бірде-бір нүкте жоқ.
интервалдар тізбегі үшін теореманың шарттары орындалса да, олардың бәрінде жататын бірде-бір нүкте жоқ.
Расында да, әрбір
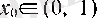 және кез келген
және кез келген
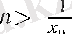 үшін
үшін
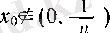 болады.
болады.
2 Монотонды тізбек бар және оның шегі . е саны. Тартылатын кесінділер принципі. Коши теоремасы
1- анықтама.
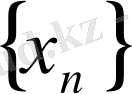 тізбегін кемімейтін (өспейтін) деп атайды, егер
тізбегін кемімейтін (өспейтін) деп атайды, егер
 n=1, 2… (1)
n=1, 2… (1)
теңсіздігі орындалса.
2-анықтама.
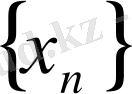 тізбегін өспелі (кемімелі) тізбек дейді, егер
тізбегін өспелі (кемімелі) тізбек дейді, егер
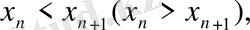 n=1; 2… (2)
n=1; 2… (2)
теңсіздігі орындалса.
Тізбектердің осы түрлерін біріктіріп жалпы атпен монотонды тізбектер деп атайды.
Теорема. Егер өспелі (кемімелі) тізбек жоғарғы (төменгі) жағынан шектелсе, онда ол жинақты.
Бұл теореманы былай да келтіруге болады:
Егер кемімейтін(өспейтін) тізбек жоғарғы (төменгі) жағынан шектелсе, онда ол жинақты.
1- ескерту. Кемімейтін және жоғарғы жағынан шектелген
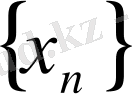 тізбегінің барлық элементтері оның шегі
тізбегінің барлық элементтері оның шегі
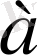 санынан аспайды:
санынан аспайды:
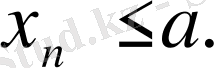
Дәл осылай өспейтін, төменгі жағынан шектелген
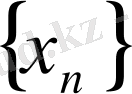 тізбегінің мүшелері оның шегі болатын а санынан кем болмайды:
тізбегінің мүшелері оның шегі болатын а санынан кем болмайды:
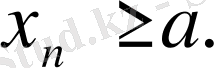
2- ескерту. Монотонды тізбектің шегі туралы теорема шектің бар болу фактысын тағайындайды, бірақ шекті анықтамайды.
Осы теореманы пайдаланып,
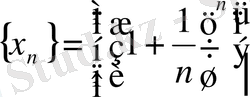 тізбегінің жинақты екені дәлелденеді және
тізбегінің жинақты екені дәлелденеді және
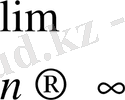
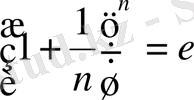 (3)
(3)
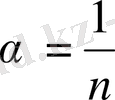 десек, онда
десек, онда
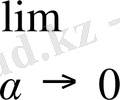
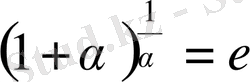 (3
1
)
(3
1
)
көреміз.
Больцано - Вейерштрасс теоремасы. Кез келген шектелген тізбектен жинақты ішкі (бөлімше) тізбекті бөліп алуға болады.
3- анықтама. Бөлімше тізбектің шегін берілген тізбектің дербес шегі деп атайды.
4- анықтама. Егер кесінділердің шексіз тізбегі
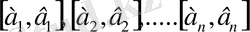 ; . . . , (4)
; . . . , (4)
үшін мына шарттар орындалса:
1)
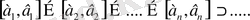 (5)
(5)
2)
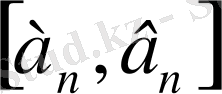 кесіндісінің ұзындығы
кесіндісінің ұзындығы
 -да
-да
 , нольге ұмтылса
, нольге ұмтылса
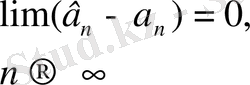 онда (4) тізбекті тартылатын кесінділер тізбегі деп атайды.
онда (4) тізбекті тартылатын кесінділер тізбегі деп атайды.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz