Нақты сандардың аксиомалары

Кіріспе
1 Нақты сандар теориясы
1.1 Нақты сандар жиыны, нақты сандардың абсолют шамасы
1.2 Натурал сан мен нөл ұғымдары.
1.3 Сан ұғымын кеңейту мәселесі..
2 Нақты сандардың аксиомалары мен негізгі қасиеттері.
2.1 Қосу жән көбейту амалының аксиомалары, қосу және көбейту амалдарының арасындағы байланыс..
2.2 Реттеу аксиомалары.
2.3 Архимед аксиомасы.
2.4 Жоғарғы және төменгі шекаралар туралы аксиома.
2.5 Қосу мен көбейту аксиомаларының салдары.
2.6 Архимед аксиомасының салдары..
2.7 Нақты санның бүтін дәрежесі мен оң санның нақты дәрежесі ... ... ..
Қорытынды .
Қолданылған әдебиеттер тізімі..
Қосымша..

Нақты caн ұғымы өте терең ұғым. Оны анықтау мәселелері әлі толық зерттелмеген.
Аксиома - дәлелдемей қабылданатын тұжырым. Аксиомалар жинағы келесі мағынада белгілі бір теорияның негізін құрайды: ол теорияның теоремаларының дәлелдеулері тек қана сол аксиомаларға сүйенеді.
Аксиоманы қанағаттандыратын кез келген R жиынын нақты сандар жиыны деп, ал оның әрбір элементі нақты сан деп аталады.
Сонымен, жиынының элементтерінің табиғатына ешқандай көңіл бөлінбейді, олардың белгілі бір қасиеттерді қанағаттандыратыны ғана ескеріледі.
Математикалық анализдің негізін қалаушылар мен сол теорияны ғасырлар бойы дамытқан ұлы математиктер дәл осы жолмен жүрген: нақты caн деген не және оның қасиеттерін қалай дәлелдеуге болады деген мәселені қарастырмай-ақ, сол қасиеттер айқын түрде орындалады деп есептеп, пайдалана берген.
Нақты сан - кез келген оң, теріс және нөл сандары. Ол рационал сандар және иррационал сандар болып бөлінеді. Нақты сан түсінігі рационал сан ұғымын кеңейтуден шыққан. Кеңейтудің қажеттілігі кез келген шаманың мәнін толық анықталған сан көмегімен өрнектеуден және математиканың ішкі дамуынан пайда болды.

1. Айдос Е.Ж. Жоғары математика. Алматы «Иль- Тех-Кітап». -2008.
2. Темірғалиев Н.Т. Математикалық анализ. Т1, Т2, Т3. Алматы: 2007.
3. Евсюк С.Л. Математика. Учебное пособие. Минск. 2010.
4. О.В.Бесов Лекции по математическому анализу, ч.1
5. В.А.Зорич Математический анализ, т.1
6. В.П.Демидович Сборник задач и упражнений по математическому анализу, ч.1
7. В.А.Ильин, Э.Г.Позняк Основы математического анализа, ч.1
8. Л.Д.Кудрявцев Краткий курс математического анализа, т.1

Пән: Математика, Геометрия
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 26 бет
Таңдаулыға:

Курстық жұмыс
Тақырыбы: Нақты сандардың аксиомалары

Мазмұны

Кіріспе ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .3
... ... ... ... ... ... ... ... .. ... ... ... ... 4
1 Нақты сандар 4
теориясы ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... .6
... ... ... ... . 9
1.1 Нақты сандар жиыны, нақты сандардың абсолют 11
шамасы ... ... ... ...
1.2 Натурал сан мен нөл 11
ұғымдары ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... .1 2
. 13
1.3 Сан ұғымын кеңейту 13
мәселесі ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... .1 4
... 19
2 Нақты сандардың аксиомалары мен негізгі 20
қасиеттері ... ... ... ... ... ... . 24
2.1 Қосу жән көбейту амалының аксиомалары, қосу және көбейту 25
амалдарының арасындағы 26
байланыс ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... .
2.2 Реттеу
аксиомалары ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ... ... ... ... ...
2.3 Архимед
аксиомасы ... ... ... ... ... ... . ... ... ... ... ... ... ... ... .
... ... ... ... ...
2.4 Жоғарғы және төменгі шекаралар туралы
аксиома ... ... ... ... ... ... ...
2.5 Қосу мен көбейту аксиомаларының
салдары ... ... ... ... ... ... ... ... ... ..
2.6 Архимед аксиомасының
салдары ... ... ... ... ... ... ... ... ... ... ... ... ... ... ..
2.7 Нақты санның бүтін дәрежесі мен оң санның нақты
дәрежесі ... ... ..
Қорытынды
... ... ... ... ... ... ... ... .. ... ... ... ... ... ... ... ... .
... ... ... ... ... ... ... ...
Қолданылған әдебиеттер
тізімі ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ...
Қосымша ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .
... ... ... ... ... ... ... ... .. ... ... ...

Кіріспе

Нақты caн ұғымы өте терең ұғым. Оны анықтау мәселелері әлі толық
зерттелмеген.
Аксиома - дәлелдемей қабылданатын тұжырым. Аксиомалар жинағы келесі
мағынада белгілі бір теорияның негізін құрайды: ол теорияның теоремаларының
дәлелдеулері тек қана сол аксиомаларға сүйенеді.
Аксиоманы қанағаттандыратын кез келген R жиынын нақты сандар жиыны
деп, ал оның әрбір элементі нақты сан деп аталады.
Сонымен, жиынының элементтерінің табиғатына ешқандай көңіл бөлінбейді,
олардың белгілі бір қасиеттерді қанағаттандыратыны ғана ескеріледі.
Математикалық анализдің негізін қалаушылар мен сол теорияны ғасырлар
бойы дамытқан ұлы математиктер дәл осы жолмен жүрген: нақты caн деген не
және оның қасиеттерін қалай дәлелдеуге болады деген мәселені қарастырмай-
ақ, сол қасиеттер айқын түрде орындалады деп есептеп, пайдалана берген.
Нақты сан - кез келген оң, теріс және нөл сандары. Ол рационал сандар
және иррационал сандар болып бөлінеді. Нақты сан түсінігі рационал сан
ұғымын кеңейтуден шыққан. Кеңейтудің қажеттілігі кез келген шаманың мәнін
толық анықталған сан көмегімен өрнектеуден және математиканың ішкі дамуынан
пайда болды.
Мысалы: сандарға орындалатын бірсыпыра амалдарды пайдалану облысын
кеңейту (түбір астынан шығару, логарифмдерді есептеу, теңдеулерді шешу және
т.б.). Нақты сандардың жалпы ұғымын ертедегі грек математиктері салыстырып
өлшеуге болмайтын кесінділер теориясында берді. Жүйелі теорияны тек 19
ғасырдың соңында Г.Кантор,Р.Дедекинд және К.Вейерштрасс жасады. Барлық
нақты сандар жиыны сан түзуі деп аталады және деп белгіленеді. Сызықты
реттелген жиын және негізгі арифмет. амалдарға (қосу мен көбейту) қатысты
өріс құрады. Сан түзуі геометриялық түзуге ұқсас, былайша айтқандадегі
сандар мен түзудегі нүктелер арасында реттілігі сақталатын өзара бірмәнді
сәйкестік орнатуға болады. Осы сәйкестіктен сан түзуінің үздіксіздігі
шығады. Түзудің үздіксіздігі жөніндегі қағида қазіргі матем. талдаудың
негізі болып табылады.
Курстық жұмыстың мақсаты: нақты сандардың аксиомаларын зертеу.
Міндеттері:
- нақты сандар теориясын зерттеу;
- нақты сандар аксиомаларын беріп, сол аксиомалардан шығатын нақты
сандардың негізгі қасиеттерін дәлелдеп көрсету.
Құрылымы: курстық жұмыс кіріспеден, негізгі екі тараудан,
қорытындыдан, қолданылған әдебиеттер тізімінен және қосымшадан құрылады.

1 Нақты сандар теориясы

1.1 Нақты сандар жиыны, нақты сандардың абсолют шамасы

Математикада негізінен сандармен жұмыс істейтін болғандықтан олардың
кейбір түрлерін келтірейік. Бүтін және оң 1,2,3...n ... сандарды натурал
сандары деп атайды. Оң және теріс, бүтін және бөлшек, бөлшектердің ішінде
ақырлы немесе шексіз периодтық ондық бөлшектер жиыны рационал сандары
болады. Шексіз периодты емес ондық бөлшектен тұратын, яғни рационал емес
сандарды иррационал сандары деп атаймыз. Рационал және иррационал сандар
жиынтығы бірігіп нақты сандар деп аталады.
Нақты сандары мен сандар осі бойындағы нүктелер арасында бір мәндік
сәйкестік болады. Нақты сандар өзара шамаларымен реттелген, яғни әрбір
екі нақты сан арасында келесі үш қатынастың біреуі орындалады ху, х=у,
ху
Нақты сандардың негізгі қасиетінің бір: екі кез келген нақты сан
арасында рационал немесе иррационал сан табылады. Бұл қасиет нақты
сандарының үзілісіздігі.
Берілген х санының абсолют шамасы деп, егер х≥0 болса, сол х санының
өзі болады, егер х0 болса абсолют шамасын анықтау үшін х-ке теріс таңба
қояды, яғни абсолют шамалардың қасиеттерін келтірейік:
а) Екі санның қосындысың абсолют шамасы (модулі) олардын абсолют
шамаларының қосындысынан аспайды:
б) Екі саның айырымының абсолют шамасы осы сандардың абсолют шамалар
айырымынан кем болмайды:
в) кез келген х және у сандары үшін және теңдіктері
орындалады.
Натурал сандар.
Натурал сандар деп мына сандарды атаймыз 0, 1, 2, 3, 4,...
Барлық натурал сандар жиының N символымен белгіленеді. Белгілі бір a
санының натурал сан екенің көрсету үшін a ∈ N деп белгілейміз. Мысалы 1 ∈
N, 5 ∈ N, 3 ∈ N.
Бүтін сандар.
Бүтін сандар деп оң және теріс таңбасымен алынған барлық натурал
сандар жиынынан құралған сандар жиының атаймыз.
Яғни бүтін сандар 0, 1, 2, 3, 4,... және -1, -2, -3, -4,... сандар
жиындарының бірігуінен құралған. Бүтін сандар жиының P символымен
белгілейміз.
Тұжырым.
N жиынына еңетің кез келген сан P жиынына да еңеді. Бұндай жағдайда N
жиыны P жиынына еңеді дейді, және N ⊆ P деп жазады.
Сұрақ.
P жиыны N жиынына еңеді ме?
Рационал сандар деп (a ∈ P, b ∈ P, b ≠ 0) сандарын атаймыз.
Мысалы 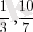. Рационал сандар жиының R деп белгілейміз.
Кез келген бүтін c саны рационал жиынына еңеді да, яғни рационал саны
да болып табылады. Өйткені 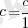, соңдықтан P ⊆ R.
Сұрақ.
N ⊆ R тұжырымы орынды ма?
Иррационал сандар.
Иррационал сан деп π = 3,141592...
немесе 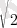= 1,4... сандары тәрізді бөлшек бөлігі шексіз, периодты емес
цифрлардан құралған сандарды атаймыз.
Иррационал сандар жиының Q деп белгілейміз.
Нақты сандардың 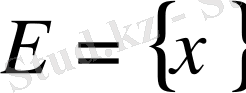жиыны берілсін.
1- анықтама. Нақты сандар жиыны Е жоғарғы (төменгі) жағынан шектелген
деп аталады, егер 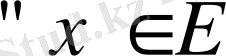элементі үшін x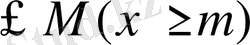теңсіздігін қанағаттандыратын
саны (m саны) табылса. Онда Е-ні жоғарғы (төменгі) жағынан шектелген
деп айтады.
М санын ( санын) Е жиынының жоғары(төменгі) шекарасы дейді.
2- анықтама. Жоғары және төменгі жақтарынан шектелген жиынды
шектелген жиын дейді.
3-анықтама. Егер Е жиыны ең болмағанда бір жағынан шектелмесе, онда Е
жиынын шектелмеген дейді.
4- анықтама. Е жиынын барлық жоғары шекараларының ең кішісін осы
жиынның дәл жоғарғы шекарасы немесе жоғары жағы деп атайды да оны sup E ,
беклгілейді.
5- анықтама. Е жиынының барлық төменгі шекараларының ең үлкенін осы
жиынның дәл төменгі шекарасы немесе төменгі жағы деп атайды да оны inf E
белгілейді.
Егер Е жиыны жоғары (төменгі) жағынан шектелмесе, онда sup
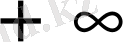
E= 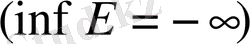жазады.
Вейерштрасс теоремасы, Кез келген бос емес жиын жоғарғы (төменгі)
жағынан шектелсе, онда оның дәл жоғарғы (төменгі) шекарасы бар.
Анықтама. х нақты санының модулі немесе абсолюттік шамасы деп
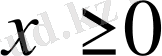болғанда х санының өзін айтады, егер x 0 болса –х санын айтады, оны
белгілейді.

Сонымен,

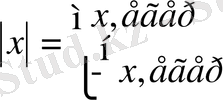
Модулдің қасиеттері:
1)
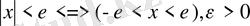
2) 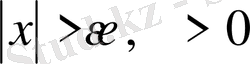, онда және
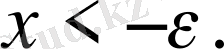
3)
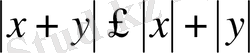
4)
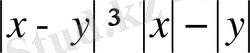
5)
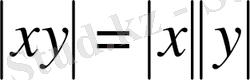
6)
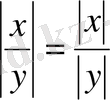
Мысалдар:
Квадраты 3 –ке тең болатын рационал саннның болмайтынын дәлелде.
Шешуі: Қарсы жорып r2 =3 болатын рационал r саны бар дейік. Онда
r = , n0 және қысқармайтын бөлшек болсын. m2 = 3n2 , бұл
m санының 3 –ке бөлінетінін көрсетеді. m =3m, десе 9m2 = 3n2
3m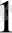2=n2. m және n сандары 3-ке бөлінеді. Бұл бастапқы шартқа
қайшы. Демек r2=3 болатын рационал сан бар деген жоруымыз дұрыс емес
екен.
Теңсіздікті дәлелде .
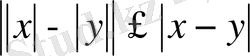Дәлелдеу. Абсолюттік шаманың қасиеті бойынша 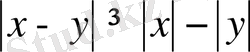және 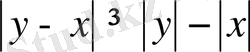.Екінші
теңсіздікті -1 –ге көбейтеміз - .
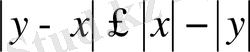Онда - немесе .
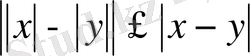Теңдеуді шеш =x2 -6.
Шешуі. Егер х0 болса, х=x2-6x2 –x -6=0, x1=3,x2=-2.
x0 болғандықтан x =3 аламыз. Ал x0 болса, -x=x2-6x2 +x-6=0,
x1=-3, x2=2, x0 болғандықтан х=-3, Жауабы: 3 және -3.

1.2 Натурал сан мен нөл ұғымдары

Сан - баста заттарды санаудың мұқтаждығынан пайда болған негізгі
математикалық ұғымдардың бірі. Ол кейін математикалык білімдердің дамуына
қарай жетілдірілді. Бұл ұғым өте ерте заманда, күллі математика
ғылымы сияқты адамдардың практикалық қызметінің қажеттігінен келіп
туды. Ол өте баяу қалыптасты, сөйтіп барған сайын күрделене
тускен соң практикалық, ал онан соң теориялық сипаттағы мәселелерді шешу
барысында көптеген ғасырлар бойы біртіндеп кеңейіп және реттеліп
отырды.
Бұл ұғымның маңыздылығы туралы ғалымдар мынандай шіукірлер айтқан.
Мәселен, Э.Борель (1871-1956): "Адамдардың білімі онда санның қандай рол
атқаратынына байланысты Ғылым атына ие болуға лайық", - деп жазды. С.Стевин
(1548-1620) былай деп жазды: "Сандардың арасында ғажайып келісімділік
пен үйлесімділіктің бары соншалық, біз олардың керемет заңдылығы туралы
күндер мен түндер бойы ойлануымыз керек...".
"Біз, - деп жазды Н.Н:Лузин (1883-1950) - бірлік ұғымын жасағаны
(ашқаны емес, нақ сол жасағаны) үшін адамның данышпандылығы алдында бас
июге тиіспіз. Сан пайда болды, ал сонымен бірге математика да пайда болды.
Сан идеясынан - ең ұлы ғылымдардың бірінің тарихы, міне, содан басталада".
Натурал сан ұғымының дамуы ерте заманда адамның заттар жиынтығының
саны оларды санамай-ақ яғни өзара бір мәнді сәйкстікті тағайындау негізінде
қабылдануымен сипатталады. Өте ұзақ дамудың нәтижесінде адам натурал
сандарды жасаудың келесі кезеңіне жетгі - жиынды салыстыру үшін аралық
жиындарды қолдана бастады. Бұл кезеңде сан саналатын жиындарлан
ерекшеленген жоқ. Адам аралық жиындарды қолдануға үйренгеннен кейін барып
қана объектілер мен аралық жиындар арасындағы ортақ нәрсені анықтады.
Аралық - жиындарды, оның элементтері табиғатынан дерексіздендіру мүмкін
болғаннан кейін натурал сан туралы түсінік пайда болды.
Уақыт өте келе адамдар сандарды атауды ғана емес, оларды белгілеуді
де, сондай-ақ олармен амалдар орындауды да үйренді. Осынау мәселелерді
шещудегі көптеген қиыншылықтар Ежелгі Үндістанда сандардың ондық жазуы мен
нөл ұғымының жасалуы нәтижесінде ғана жойылды. Әуелде санның жоқтығын
білдіртен нөл теріс сандар ұғымы енгізілгеннен кейін ғана сан ретінде
карастырылатын болды. Натурал сандар жиынының шексіздігі туралы түсінік те
біртіндеп калыптасты. "Натурал сан" терминің тұңғыш рет римдік ғалым
А.Боэций (шамамен 480-524 жылдар) қолданған.
Санаудың ондық жүйесі түрінде біздің заманымыздың шамамен VI ғасырында
Үндістанда қалыптасты. Нөл үшін ерекше белгі енгізу үндістандық ғылымның
маңызды жетістігі болады. Нөл енгізілгеннен кейін ғана жазудың ондық жүйесі
толығынан аяқталды. Алдымен нөлдің абақтың тиісті разрядында тастардың
жоқтығын белгілеу үшін пайда болуы да ықтимал.
Натурал сан ұғымы қалыптасқаннан кейін сандар дербес өбъектілерге
айналды және оларды математикалық объектілеу ретінде зерттеудің мүмкіндігі
пайда болды. Арифметика -сандарды және олармен жүргізілетін амалдарды
зеттейтін ғылым, Ежелгі Шығыс елдерінде: Вавилонда, Қытайда, Үндістанда,
Египетте дүниеге келді. Осы елдерде жинақталған математикалық білімдерді
Ежелгі Грецияның ғалымдары дамытып, жалғастырды. Орта ғасырда арифметиканың
дамуына Үндістанның, араб елдері мен Орта Азия математиктері, ал XII
ғасырдан бастап - европалық ғалымдар үлес косты.
Сөйтіп, ежелгі дүние ғалымдарының еңбектерінің өзінде - ақ натурал
сандардың қатарының шексіздігі анықталды (б.д.д III ғ.). Натурал қатардың,
жай сандар қатарының шексіздігі жайында және соншалық үлкен сандар
атауларын жасау Евклидтің "Бастамалар" деген әйгілі туындысында және
Архимедтің "Құмды санау туралы ("Псаммит") деген кітабында карастырылады.
XIX ғасырда ғалымдардың назары натурал санның
математикалық теорияларын, яғни натурал сандармен есептеулер іжүргізуге
негіз болған теорияларды құруға және логикалық тұрғыдан негіздеуге
аударылды. Санның натурал қатарындағы терең заңдылықтарды зеттеу қазіргі
уақытқа дейін жалғастырылып, сандар теориясын да дамытуда.
Натурал сандар ұғымының соншалық қарапайым болып көрінетіні
сондай, ғылымда ұзақ уақыт бойы оны қандай да болсын қарапайым ұғымдардың
терминдерімен анықтау туралы мәселе қойылған жоқ.
Натурал санды және сандардың натурал катарын анықтаудың мейлінше әр
түрлі жолдары және соған сәйкес натурал сандар жиынындағы операциялар
(амалдар) мен қатынастарды енгізуге қатысты да түрліше жолдар орын алып
келеді. Натурал сандар жиынымен бір ғана элементтен - 0 санынан тұратын
жиынның бірігуі болып табылатын теріс емес бүтін сандар жиынын құрудың
әртүрлі жолдары осыған байланысты.
Теріс емес бүтін сандар жиынын құрудың теориялық-жиындық тәсілі
тұрғысынан, натурал сан деп бос емес шектеулі бір-бірімен эквивалентгі
жиындар класының ортақ қасиетін айтады. Ондай тәсіл мейлінше көрнекі және
істің шын мәнісінде мектепке өтілетіндерге дәл келеді. Алайда оның бір
елеулі кемшілігі бар: негізгі ұғым - шектеулі жиын, бұл жағдайда белгісіз
болып қалады (анықталмайды).
Шектелу жиындардың айырмашылыктарын түсіндірген кезде, әдетте,
шектеулі жиындар барлық элементтерін "толық атап шығуға", бірінен соң бірін
оларды "көрсетіп беруге" болатын жиындар дейді, немесе бұлар элементтерін
"санап шығуға" болатын жиындар деп аталынады.
Бірінші жағдайда біз тәжірибе мен интуицияға (сезімге) негізделген
сипаттаумен істес боламыз, ал екінші жағдайда - кайта есептеуге сілтеме
жасау, мәнісі жөнінен жиынның "натурал катар кесіндісіне" бейнелеуін
білдіреді де, натурал сан туралы тұжырымдалып қойған ұғымды қолдануды
көздейді. Натурал сан ұғымына негізделиеген шектеулі жиын ұғымының мүмкін
болатын формальді анықтамалары бастапқы арифметиканың мектептік курсын
құруға негіз бола адмайды.
Сондықтан сандық теорияда натурал сан әуес баста-ақ шектеулі жиын
элементтерінің саны ретінде, яғни жалпы ұғым болып табылатын кез-келген
жиынның қуаты ұғымының жеке жағдайы ретінде қабылданғанымен, натурал сандар
арифметикасын бастапқы оқыту натурал сандар туралы алғашқы түсініктерді
қалыптастырудың нақты жолдарын ескемей кете алмайды.
Сондықтан натурал сандар заттарды санау кезінде қолданылады деп
есептейді. Санау процесшде реттік натурал сандарды пайдаланылады, ал
жиынның барлық элементтерін санап шыккан соң осы жиынның сандық
сипаттамасын алады. Басқа сөзбен айтқанда, санау кезінде сандардың натурал
қатарының кесіндісін пайдаланылады.

1.3 Сан ұғымын кеңейту мәселесі

Біз натурал сан мен нөл ұғымдарының қалай пайда болып, қалай дамығанын
білеміз Сондай-ақ бұған дейін теріс емес бүтін сандар жиынын (Ко немесе Ео)
әр түрлі) финиттік, теориялық-жиындық және аксиоматикалық) тұрғыдан құруды
да қарастырғанбыз. Мұнымен қоса натурал санды шамаларды өлшеудің
нәтижесінде шығарып алуға болатындығын да оқығанбыз, яғни өлшенетін шаманы
әрқайсысы өлшем бірлігіне тең бірнеше бөліктерге бөлу, қандай да болсын,
әйтеуір бер мағынада мүмкін болса, онда өлшеу нәтижесі (немесе шаманың
өлшемі) натурал сан арқылы өрнектеледі.
Жалпы алғанда, сан және фигура ұғымдары, басқа ешқайдан емес, тек
шындық дүниеден алынған. Адамдардың санауға үйренген, яғни алғашқы
арифметикалық есеп шығаруға үйренген он саусағын не десеңіз ол деңіз, тек
әйтеуір ол ақыл-ойдың еркін творчествосының жемісі емес. Санау үшін,
саналуға тиісті нәрселердің болуы ғана емес, сонымен бірге, бұл нәрселерге
көз жібергенде, олардың санынан басқа қасиеттеріне алаңдамайтын қабілет те
болу керек, ал ол қабілет - тәжірибеге сүйенген ұзақ тарихи дамудың
нәтижесі.
Натурал сандардың N жиыны сан ұғымын кеңейту процесіндегі бастапқа
жиын болып табылады. Өте ерте заманда пайда болған натурал сан ұғымы
көптеген ғасырлар бойы жалпыланып, кенейе түсті. Сонда сан жайындағы
түсініктер адамзаттың практикалық мұқтаждығына, мәселен, шамаларды
өлшеудің қажеттігіне және математиканың өзінің ішкі
мұқтаждығына байланысты кенейіп отыратындығы байқалады. Мысалы, шамаларды
неғұрлым дәлірек өлшеудің мұқтаждығы оң бөлшек ұғымының тууына себепші
болса, теңдеулерді шешу тәжірибелері мен осы саладағы теориялык
зерттеулерге байланысты теріс сандар ұғымы пайда болды. Бастапқыда
санның жоқ екендігін белгілеу үшін қолданылған нөл, теріс сандар
енгізілгеннен кейін, 2 бүтін сандар жиынындағы, сондай-ақ 3 рационал
сандар жиынындағы толыққанды сан ретінде карастырылатын
болды.
Б.э.д. V ғасырда, Пифагор мектебінде кесінді ұзындығын дәл өлшеу үшін
оң рационал сандардың жеткіліксіз болатындығы тағайындалды. Кейінірек, осы
мәселенің шешілуіне байланысты иррационал сандар пайда болды, ал
XVI ғасырда ондық бөлшектердің енгізілуіне байланысты нақты сандарға
қарай қадам жасалды. Нақты санның қатаң түрдегі анықтамасы мны нақты сандар
жиынының қасиеттері XIX ғасырда тұжырымдалды.
Нақты сан ұғымы сандар қатарындағы ең соңғы ұғым емес. Сан ұғымын
кеңейту прцесін одан әрі жалғастыра беруге болады және бұл процесс
жалғасады да - мүны математиканың және басқа да ғылымдардың дамуы талап
етуде. Мәселен, комплекс сандар теріс сандар сияқты, математика ғылымының
іштей дамуына, атап айтқанда алгебралык теңдеулерді шешу тәжірибесіне
байланысты пайда болды. Тарихи тұрғыдан алғанда, комплекс сан ұғымы XVI
ғасырда екінші дәрежелі теңдеулерді шешу мәселесінен келіп шыққан. Комплекс
сандар нақты сандар сияқты мөлшерді сипаттағанымен, нақты сандар
терминдерінеде құрастырылған есептерді шешуде оларды қолданудың пайдасы
тиеді. Таза математикалық есптерді шешу барысында да комплекс сандарды
қолдану маңызды болып саналады.
Сан ұғымын жалпылау барысында қазіргі кезде гиперкомплекс сандар ұғымы
келіп шықты. Гиперкомплекс сан ұғымы комплекс санға қарағанда неғұрлым кең
ұғым. Гиперкомплекс сандардың қарапайым мысалы физика мен техникада, атап
айтқанда электр және элкетро-техника теориясында қолданылатын векторлық
алгебраның дауына себепші болған кватерниондар болып табылады. Сондай-ақ,
самолет қанатының прфилін (пішінін) анықтау мен самолет теориясының негізгі
заңдылықтарын қорытындылауда комплекс сандарлың қолданылуын ерекше атап
айтуға болады.
Сан жайындағы жаңа түсініктердің пайда болумен бірге осы жаңа сандық
объектілерге амалдар қолдану ережелерін негіздеу қолға алынып отырылды.
Алайда, сандар және оларға қолданылатын амалдар жайындағы жинақталған
мәліметтер математикалық теория ретінде XIX ғасырдың екінші жартысында,
көптеген көрнекі математиктер математиканы негіздеу мәселесімен айналыса
бастағанда ғана бір жүйеге келтірілді.
Қазіргі кезде әр түрлі сандық жиындарды мына ретпен қарастыру
қабылданған: натурал сандар (Ы жиыны), бүтін сандар (2 жиыны), рационал
сандар (С жиыны), нақты сандар (К. жиыны), комплекс сандар (С жиыны)

2 Нақты сандардың аксиомалары мен негізгі қасиеттері

2.1 Қосу жән көбейту амалының аксиомалары, қосу және көбейту
амалдарының арасындағы байланыс

1-аксиома. Кез келген реттелген а және b сандары үшін: а + b
символымен белгіленетін үшінші caн сәйкес қойылады. а + b саны а мен b
сандарының қосындысы деп аталады.
Мұнда реттелген деген сөз a — бірінші, ал b екінші сан ретінде
алынатынын білдіреді. Оны үлкен-кіші ұғымымен жаңылыстырмау керек.
2-аксиома. Әрқашанда, a + b = b + a.
а мен b сандарын қосу амалының анықтамасында олардың реті ескерілді,
ал а+ b және b + а сандары өзара тең болатыны жөнінде ештеңе айтылмайды.
Бұл аксиома сол екі caн тең болатынын тұжырымдайды.
3-аксиома. Әрқашанда а+ (b + с) — (а + b) +с.
1-аксиомада кез келген реттелген қос сандар үшін олардың қосындысы
анықталған, ал a + b + с символына әзірше ешқандай мағына берілмеген. Егер
анықтама бойынша a + b + c = a+(b + c) болады деп алсақ, онда 2 және 3
аксиомалардаи бұл анықтаманың оң жағын (a + b)+c, (a+c)+b, (b + c)+a,
b+(a+c), с+(а + b) өрнектерінің әрқайсысына өзгертсек, нәтижесі
өзгермейтінін көреміз, яғни a, b және с үш санның қосындысы ретінде тек
қана бір сан сәйкес келеді.
Дәл осылай төрт, бес, ... қосылғыштың қосындысы анықталады.
4-аксиома. Белгілі бір 0 саны мен кез келген а саны үшін а + Ө = а
орындалады. 0 саны ноль деп аталады да, 0 символымен белгіленеді.
Сонымсн, әрбір а саны үшін а + 0 = а.
5 - а к с и о м а. Әрбір а саны үшін а+а' = 0 теңдігі орындалатын а'
саны табылады.
а' саны а санына қарама-қарсы сан деп аталады да, — а символымен
белгіленеді. Сонымен, а+( — а)=0.
6-аксиома. Кез келген реттелген а және b сандары үшін олардың
көбейтіндісі деп аталып, а•b символьтмен белгіленетіи үшінші caн сәйкес
қойылады.
7-аксиома. Әрқашанда, a•b = b•a.
8-аксиома. Әрқашанда, (а • b) • с = а • (b • с).
Қосындылар жағдайындағыдай, 7- және 8-аксиомалар бойынша үш, төрт,
бес, ... сандардың көбейтіндісі де анықталады. Мысалы, a • b • с = а- (b
• с).
9 - а к с и о м а. Белгілі бір саны мен кез келген а саны
үшінтеңдігі орындалады.саны бір деп аталады да, 1 символымен
белгіленеді. Сонымен, кез келген а үшін 1•а = а.
1 санын қосылғыш ретінде бірте-бірте алып 1, 2=1 + 1, 3 = = 2 + 1, ...
, ... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.