Функцияны Тейлор және Маклорен қатарына жіктеу: формула, қалдық мүшелер және қолданылуы


Курстық жұмыс
Тақырыбы: Тейлор формуласының қолданылулары
Мазмұны
Кіріспе . . .
1 Тейлор формуласының сипаттамасы . . .
1. 1 Тейлор формуласы . . .
1. 2 Тейлор қатары . . .
1. 3 Кейбір функциялар үшін Маклорен қатарлары . . .
2 Тейлор формуласының қолданылуы . . .
2. 1 Функция және оның түрлері, оларды есептеп шығару теоремалары, Тейлор теоремасы . . .
2. 2 Аралас туындылар туралы теорема, жоғарғы ретті дифференциалдар. Екі айнымалылы функция үшін Тейлор формуласы . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
3
6
6
7
7
9
9
14
19
20
Кіріспе
Математика (грек. mathematike- білім, ғылым) - ақиқат дүниенің сандық қатынастары мен кеңістік формалары жайлы ғылым. Көрнекті совет математиктері А. Н. Колмогоров пен А. Д. Александров ұсынған жіктеу бойынша математиканың даму тарихы шартты түрде төрт кезеңге бөлінеді.
Бірінші кезең- математиканың білім- дағдыларының қорлану, жинақталу дәуірі. Ол ерте кезден басталып б. з. б. 7-6 ғасырларына дейін созылды. Бұл дәуірде математика адамзат практикасы мен тәжірибесіне тікелей тәуелді болды, солардан қорытылған ережелер жинағынан тұрды. Екінші кезең- математиканың өз алдына дербес теориялық ғылым болып туу, қалыптасу кезеңі. Мұнда арифметика, геометрия, алгебра, тригонометрия айрықша теориялық пән болып қалыптасты. Бұл кезең тұрақты шамалар математикасының, кейде элементар математика кезеңі деп аталады. Ол екі мың жылға жуық мерзімге созылып, шамамен 17 ғасырда аяқталады. Үшінші кезең- айнымалы шамалар математикасы немесе жоғары математиканың туу, қалыптасу кезеңі. Бұл 17 ғасырда басталып, 19 ғасырдың 2-жартысына дейін созылды. Жиындар теориясына байланысты анализдің, геометрияның және алгебраның жаңа сападағы салалары шыққаннан кейін, математиканың негізгі мәселелерін жалпы қарастыру кезеңін төртінші кезеңге жатқызуға болады. Ол- 19-20 ғасырларды қамтитын қазіргі математика кезеңі.
Математиканың бастапқы мағлұматтары барлық халықтарда болған. Ғылымның дамуына әсіресе Египетте(Мысыр), Вавилонда жинақталған мәдени дәстүрлердің ықпалы үлкен болды. Бұл елдерде б. з. б. 4-5 мың жылдай өзіндік мәдениет өркендеп, ғылыми білім қорланған. Календарь жасау, құрылыс, жер суару, жер және әр түрлі ыдыс көлемін өлшеу, теңізде жүзу, жан- жақты байланыс жасау ісі математикалық білім- дағдылардың дамуын талап етті, оның бастапқы қарапайым ережелері дәлелдеусіз қалыптаса бастады. Египетте санды иероглиф арқылы кескіндеу пайда болды, бүтін, бөлшек сандарға арифметикалық төрт амал қолдану ережелері мәлім болды. Бір белгісізі бар теңдеулер, сондай-ақ қарапайым арифметикалық және геометриялық прогрессияларға келтірілетін есептер шығару тәжірибесі кездеседі. Египеттіктер төртбұрыштың, трапецияның, үшбұрыштың ауданын, параллепипед пен табаны квадрат пирамиданың көлемін дәл есептей білген, дөңгелек ауданын жуықтап тапқан. Вавилондықтар санаудың позициялық алпыстық жүйесін қолданған. Олар сандарды көбейту, квадраттау, квадрат және куб түбір табу, бөлу таблицаларын жасады; бірінші, екінші, аракідік үшінші дәрежелі теңдеуге келтірілетін есептерді шеше білген. Вавилондықтардың геометриялық білім-дағдылары египеттіктермен деңгейлес. Алайда олар астрономиялық өлшеулер(бұрыш өлшеу тәрізді) жүргізгендіктен тригонометриялық білімдерден де хабардар болған. Пифагор теоремасы да вавилондықтарға белгілі болған. Египет пен Вавилонда б. з. б. 3-5 мың ж. арифметикалық амалдар қолдану, аудан мен көлем табу, таблицалар жасау, біртектес есептер шығару әдістерін жасау тәріздес көптеген математикалық білім- дағдылардың жинақталғанын көреміз. Бұл мағлұматтар мен дәстүрлер математиканың өзінше зерттеу пәні, әдістері бар дербес ғылым болып бөлініп шығуына жағдай жасады.
Элементтар математика кезеңі. Ежелгі Греция. Әр түрлі арифметикалық әдістер мен аудан, көлем табудың тәсілдері жөнінде нақты материалдар жинақталғаннан кейін ғана(б. з. б. 7 ғасырдан) математика Ежелгі Грецияда дербес ғылым дәрежесіне көтерілді. Грек ғалымдарының ( Фалес, Пифагор, Детель, Гиппократ, Евдокс, Аристотель, Евклид, Архимед, Аполлоний т. б. ) еңбектері арқылы математика бірте-бірте практикалық мәселелерді ғана шешуге бағытталған жалаң эмпирикалық ғылымнан өзінің нәтижелерін түпкі қағидаларын (аксиомалардан) логикалық қорытынды түрінде шығаратын дедукциялық ғылымға айналды. Бізге жеткен деректерге қарағанда геометриялық шындықтарды дәлелдеу практикасын Фалес енгізген болу керек(б. з. б. 7 ғасыр) . Фалес дәлелдепті деп саналатын теоремалар: диаметр дөңгелекті қақ бөледі; тең бүйірлі үшбұрыштың табанындағы бұрыштары тең болады; екі түзу қиылысқанда тең бұрыштар пайда болады; сәйкес екі бұрышы және қабырғасы тең екі үшбұрыш тең болады. Бұл теоремаларды оның қалай дәлелдегені нақты дерек жоқ.
Грецияда теориялық математиканың туып өркендеуіне шешуші еңбек сіңірген екінші бір ғылыми- философиялық мектеп атақты Пифагор мектебі болды. Пифагор ғылымның төрт саласын( арифметика, музыка, геометрия, астрономия) ажыратып, бұл бағытта терең зерттеулер жүргізген. Бұл ғылым тарауларын гректер « математа» деп атаған, осыдан « математика» деген термин қалыптасқан. Математикалық анализ бен математикалық физика дамуының геометрия мен алгебрадағы жаңа идеялармен түйіндесуі нәтижесінде математика мен оның қолдануында ерекше маңызды қызмет атқарып отырған математиканың үлкен бір жаңа саласы- функционалдық анализ жасалды. Статистикалық физика мен әр түрлі мәселелерді зерттеуге статистикалық әдістерді кең қолдану әрекеті ықтималдықтар теориясының алдына көптеген жаңа міндеттер қойды. Осы негізде бұл теория 19-20 ғасырларда күшті қарқынмен дамытылды. 19-20 ғасырлар бойы математиканың көне салалары да жаңа идеялармен, нәтижелермен толығып, дамып отырды. Мысалы, сандар теориясына математикалық анализ әдістерін қолдану бұрын элементар әдістер арқылы шешілмей келе жатқан көптеген мәселелерді шешуге мүмкіндік берді ( мысалы, Гольдбах прблемасы) .
Теориялық математиканың зерттеулер нәтижесін практика жүзінде қолдану шешілуге тиісті есепке ( мәселеге) сан түрінде жауап алуды талап етеді. Осыған байланысты 19-20 ғасырларда математикадағы сандық әдістер оның дербес бір тармағына айналды. Көп еңбек тілейтін есептеуді қажет ететін мәселелерді шешуді жеңілдету, жеделдету ісі әуелі механика-математикалық машиналар мен аспаптарды, ал 20 ғасырдың 40 жылдарынан бастап тез әрекетті электрондық есептеуіш машиналарды талап етті. 19-20 ғасырларда дамытылған математиканың бір тармағы математикалық логика басқару туралы ғылым- кибернетикада және есептеу техникасында қолданыла бастады. Есептеу техникасының кең қолданылуына байланысты программалау теориясы пайда болды.
19 ғасырдың 2- жартысынан бастап математика тарихын қарастыру жедел қолға алынды. 20 ғасырдың 50 жылдарынан бастап математика ғылымының басқару теориясы, кибернетика, алгебралық геометрия, информация теориясы т. б. көптеген жаңа салалары пайда болды. Математиканың осылай қауырт дамуына жаратылыс тану ғылымдары мен техниканың математика алдына қойып отырған талаптары түрткі болды. Мысалы, өндірістік процесті автоматтандыру басқарудың математикалық теориясының тууына себепкер болды.
Курстық жұмыстың тақырыбы: Функцияны Тейлор қатарына жіктеу.
Мақсаты: Тейлор формуласының қасиетін аша отырып. Функцияны Тейлор қатарына жіктеу жолдарын қарастыру.
Міндеттері:
- Тейлор формуласын зерттеу;
- Функцияны Тейлор қатарына жіктеуін сипаттау, зерттеу.
Құрылымы:
- Кіріспе;
- Негізгі бөлім: екі тарау;
- Қорытынды;
- Қолданылған әдебиеттер тізімі.
1 Тейлор формуласының сипаттамасы
1. 1 Тейлор формуласы
Жуық Формула - ф(х) ≈ф*(х) +ε(х) түріндегі формуладан алынатын ф(х) ≈ф*(х) формуласы [мұндағы ε(х) - қалдық мүше немесе қателік деп қарастырылады, яғни бағаланғаннан кейін алынып тасталатын аз шама] . Мысалы, х аз шама болғанда (1+х) 2= =1+2х+х2 дәл формуласынан (1+х2) ≈1+2х Жуық формуласы алынады. Бұл жуық формула х 0-ге жақындаған сайын дәлірек нәтиже береді. Бірақ үнемі бұлай бола бермейді. Мысалы, тгх≈ жуық формуласының дәлдігі х неғұрлым π/2-ге жақындаған сайын арта түседі. Жуық формула көбінесе функцияны қатарға (мысалы, Тейлор қатарына) жіктеу арқылы алынады. Жуық формуланы сенімді түрде қолдану үшін функцияның дәл және жуық өрнегі арасындағы айырманың бағасын білу қажет.
Жуық формулалар - функцияның мәндерін есептеу үшін жуық формулалар қолданылады. Жуық формулалар алудың негізгі әдісі - функцияны қатарға жіктеу. Көбінесе функция Тейлор қатарына жіктеледі. Функцияның нақты және қатар көмегімен есептелген жуық мәндері арасындағы айырымды бағалау үшін, қатардың толықтауыш мүшесі қарастырылады. Мысалы, жуық формулалар Тейлор қатары арқылы алынса, онда осы қатардың Пеано, Шлемильх және Роша, Лагранж, Коши түріндегі толықтауыш мүшелерінің бірі бағаланады.
ф ( х ) а нүктесі төңірегінде шексіз дифференциалдана алатын функция болсын. Формальды қатар
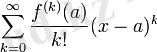
ф функциясының а нүктесіндегі Тейлор қатары деп аталады.
Теорема:
ф
(
х
)
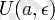 а
нүктесінің белгілі төңірегінде
н
+ 1 туындысы болсын
а
нүктесінің белгілі төңірегінде
н
+ 1 туындысы болсын
Пусть
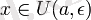
Пусть п - кез келген оң сан,
онда:
х
<
а
үшін
 нүктесі
нүктесі
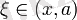 немесе
х
>
а
болғанда
немесе
х
>
а
болғанда
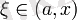 :
:
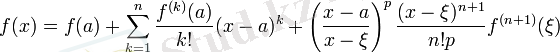
1. 2 Тейлор қатары
Тейлор қатары - функцияны көрсеткішті функциялар шексіз қосындысы ретінде жазу. Тейлор қатарының дербес қосындылары болып Тейлор көпмүшелігі саналады. Рн(х) =ф(х) -Сн(х) Тейлор қатарының қалдық мүшесі, мұндағы Сн(х) - Тейлор қатарының алғашқы н+1 мүшесінің қосындысы. болғанда Тейлор қатары ф(х) функциясына жинақты болады, яғни формуласы шығады. Бұл формуланы 1715 жылы ағылшын математигі Б. Тейлор (1685 - 1731) тапқан, х0=0 болған кезде Маклорен қатары шығады. Осыған сүйене отырып, негізгі элементар функциялардың Тейлор қатарына жіктелуін жазуға болады.
Маклорен қатары, f(z) функциясы үшін Маклорен қатары - түріндегі дәрежелік қатар. 1742 жылы Колен Маклорен (1698 - 1746) қарастырған. Егер f(z) функциясы аналитикалық нөлде дәрежелік қатарға жіктелетін болса, онда ол қатар маклорен қатарымен сәйкес келеді. Егер функция m айнымалысынан тәуелді болса, онда маклорен қатары еселідәрежелік қатарға жіктеледі: мұндағы, k=(k1, k2, . . . , km), k - теріс емес бүтін сан. Маклорен қатары Тейлор қатарының дербес жағдайы.
1. 3 Кейбір функциялар үшін Маклорен қатарлары
Экспонента:
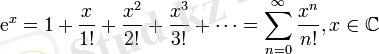
Натурал логарифм:
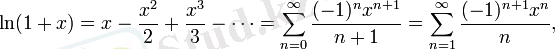 барлық
барлық
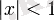 үшін
үшін
Биномдық жіктеу:
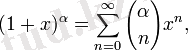 барлық
барлық
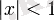 үшін және барлық
үшін және барлық
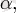 комплекс ан үшін, мұндағы
комплекс ан үшін, мұндағы
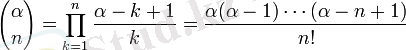
Жекеше түрі:
квадраттық түбір:
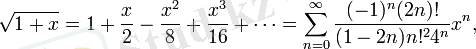 барлық
барлық
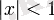 үшін
үшін
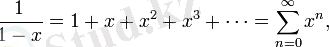 барлық
х
< 1 үшін
барлық
х
< 1 үшін
Шекті геометриялық қатар:
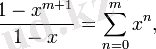 барлық
барлық
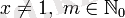 үшін
үшін
Тригонометриялық функциялар:
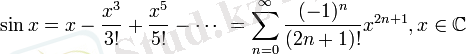
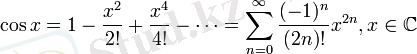
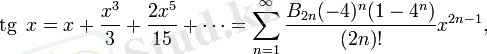 барлық
барлық
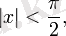 үшін, мұндағы
Б
2
н
- Бернулли сандары
үшін, мұндағы
Б
2
н
- Бернулли сандары
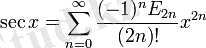 барлық
барлық
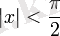
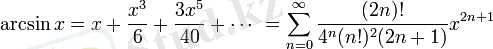 барлық
барлық
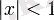 үшін
үшін
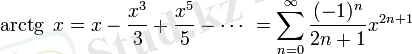 барлық
барлық
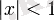 үшін
үшін
Гиперболалық функция:
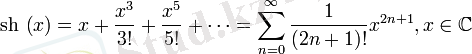
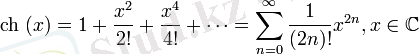
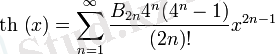 барлық
барлық
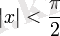 үшін
үшін
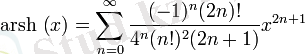 барлық
барлық
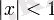 үшін
үшін
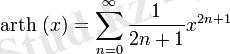 барлық
барлық
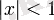 үшін
үшін
2 Тейлор формуласының қолданылуы
2. 1 Функция және оның түрлері, оларды есептеп шығару теоремалары, Тейлор теоремасы
Дифференциалдық есептеулердің маңызды есептерінің бірі функцияны зерттеудің жалпы амалдарын қарастыру болып табылады.
у=ƒ(х) функциясы қандай да бір интервалда өспелі (кемімелі) деп аталады, егер х 1 <х 2 үшін ƒ(х 1 ) <ƒ(х 2 ) (ƒ(х 1 ) >ƒ(х 2 ) ) теңсіздігі орындалса, яғни аргументтің үлкен мәніне функцияның үлкен мәні сәйкес келсе.
Функцияның өсу белгілерін атап өтейік.
1. Егер [а; b] кесіндісінде дифференциалданатын y=ƒ(x) функциясы өспелі (кемімелі) блса, онда осы кесіндіде функцияның туындысы теріс емес (оң емес), ягни f΄(x) > 0 (f΄ (х) < 0) .
2. Егер [a; b] кесіндісінде үздіксіз және оның ішінде дифференциалданатын функцияның оң (теріс) туындысы бар болса, онда функция осы кесіндіде өседі (кемиді) .
y=f(x) функциясы қандай да бір интервалда кемімейтін (өспейтін) деп аталады, егер осы интервалдан алынған кез-келген х 1 <х 2 үшін ƒ(х 1 ) ≤ ƒ(x 2 ) (ƒ(х 1 ) ≥ f(x 2 ) ) теңсіздігі орындалса.
Функция кемімейтін немесе өспейтін интервалдар функцияның монотондық интервалдары деп аталады. Функцияның туындысы нөлге айналатын немесе үзілетін нүктелері оның кризистік нүктелері деп аталады.
Егер кез-келген Δх≠0 шексіз аз үшін f(x 1 +Δx) <f(x 1 ) теңсіздігі орындалса, онда х 1 нүктесі y=f(x) функциясының локальды максимум нүктесі деп аталады. Егер кез-келген Δх≠0 шексіз аз үшін f(x 2 +Δx) >ƒ(x 2 ) х 2 теңсіздігі орындалса, онда х 2 ннүктесі у=f(x) функциясының локальды минимум нүктесі деп аталады. Максимум және минимум нүктелері функцияның экстремум нүктелері деп аталады.
Теорема 1 (локальды экстремумның қажетті шарты) . Егер y=f(x) функциясының х=х 0 нүктесінде экстремумы бар болса, ондаƒ΄(х 0 ) =0 немесе f(x 0 ) жоқ.
Теорема 2 (локальды экстремумның бірінші жеткілікті шарты) . y=f(x) функциясы х=х 0 нүктесі жататын қандай да бір интервалда үздіксіз және осы интервалдың барлық нүктелерінде дифференциалдансын. Егер х<х 0 болғанда f(x) >0, ал х>х 0 болғанда f(х) <0 болса, онда х=х 0 нүктесінде у=f(x) функциясының максимумы бар. Егер де х<х 0 болғанда f(x) <0, ал х>х 0 болғанда f(x) >0 болса, онда х=х 0 нүктесінде y=f(x) функциясының минимумы бар.
Теорема 3 (локальды экстремумның екінші жеткілікті шарты) . y=f΄(x) функциясы екі рет дифференциалдансын және f(х 0 ) =0 болсын. Онда х= х 0 нүктесінде функцияның локальды максимумы бар, егер f"(х 0 ) <0 және локальды минимумы бар, егер ƒ"(х 0 ) >0 болса.
f"(х 0 ) =0 болса, онда х=х 0 нүктесінде экстремум болмауы да мүмкін.
Функцияның дөңестігі және ойыстығы. Иілу нуктелері.
Функция графигінің асимптоталары.
y=f(x) функциясымен берілген қисық (a; b) интервалында дөңес деп аталады, егер қисықтың барлық нүктелері осы интервалдағы оның кез-келген жанамасынан жоғары жатпаса және (а; b) интервалында ойыс деп аталады, егер қисықтың барлық нүктелері осы интервалдағы оның кез-келген жанамасынан төмен жатпаса.
Қисықтың дөңес бөлігін ойыс бөлігінен бөліп жататын М(х 0 , f(x 0 ) ) нүктесі қисықтың иілу нүктесі деп аталады. М нүктесінде қисықтың жанамасы бар деп есептеледі.
Теорема (функция графигінің дөңестігінің (ойыстығының) жеткілікті шарты) . Егер (а; b) интервалының барлық нүктелерінде y=f(x) функциясының екінші туындысы теріс (оң), яғни f"(x) <0 (f"(x) >0) болса, онда y=f(x) қисығы осы интервалда дөңес (ойыс) .
Иілу нүктесінде функцияның екінші туындысы өзінің таңбасын өзгертеді, сондықтан ол нөлге айналады немесе жоқ болады.
Теорема (иілу нүктесінің жеткіліктілік белгісі) . Егер х=х 0 нүктесінде ƒ"(х 0 ) =0 немесе ƒ"(х 0 ) жоқ болса және осы нүктеден өткенде f"(x) өзінің таңбасын өзгертсе, онда абсциссасы х=х 0 болатын нүкте y=f(x) қисығының иілу нүктесі.
L түзуі y=f(x) қисығының асимптотасы деп аталады, егер қисықтың М нүктесінен L түзуіне дейінгі қашықтық М нүктесі шексіздікке ұмтылғанда нөлге ұмтылса.
Егер х = х i (і=1, . . . , п) нүктелері бар болып
lim f(x) = ±∞, болса, онда х = х i түзулері у=ƒ(х) қисығының тік
(вертикаль) асимптоталары деп аталады.
Егер ƒ(х)
k= lim--, b= lim (ƒ(х) -kх), шектері бар болса, онда
х→∞ х х→∞
y=kx+b түзлері y-f(x) қисығының көлбеу асимптоталары деп аталады. (k=0 болғанда, көлденең (горизонталь) асимптотасы) .
Көп айнымалылы функция ұғымы, оның шегі, үздіксіздігі.
Жаратылыстанудың көптеген мәселелерін қарастырғанда, айнымалылар арасында біреуінің бірнеше айнымалыға тәуелді болатын жағдайлары жиі кездеседі. Мәселен, қабырғалары х және у болып келген төртбұрыштың ауданы х және у айнымалыларының мәндері арқылы анықталады, ал қабырғаларының ұзындықтыры х, у, z - тік параллепипедттің көлемі х , у және z үш тәуелсіз айнымалылардың мәндеріне байланысты анықталады.
Аныктама 1. Айталық X, Ү және Z - қандай да бір сандық жиындар болсын. Екі айнымалының функциясы деп, хєХ, уєУ, zєZ болатындай реттелген (х; у; z) үштігінің f жиынын айтады және әрбір реттелген (х; у) сандар пары бұл жиынның бір тек бір ғана үштігіне енеді, ал әрбір z бір үштіктің ең болмағанда біреуіне кіреді. Мұндай кезде реттелген (х; у) сандар парына z саны сәйкес қойылды делініп, z=f (x; у) деп жазады. z саны f функциясының (х; у) нүктесіндегі мәні. z - тәуелді айнымалы, ал х және у - тәуелсіз айнымалылар (немесе аргументтер) ; {(х; у) } жиыны - функцияның анықталу облысы, ал z жиыны-функцняның мәндер жиыны.
Екі айнымалының функциясын z=f(x; у) деп белгілейді.
Екі айнымалының функцияның шегі ұғымын қарастыру үшін берілген М 0 (х0; у0) нүктесінің δ - аймағы және жазықтықтың жинақты нүктелер тізбегі ұғымын енгізейік.
Аныктама 2. х және у координаталары ( х - х0 ) ² + (у-у0) ² < δ теңсіздігін қанағаттандыратын, немесе, қысқаша, ρ(М; М 0 ) < δ, барлық {М(х; у) } нүктелер жиыны, М 0 ( х0 ; у0) нүктесінің δ -аймағы деп аталады.
М 1 (х 1 ; у 1 ), М 2 (х 2 ; у 2 ), . . . , М п (х п ; у п ), . . . нүктелер тізбегін қарастырайық. Оны қысқаша {М п } деп белгілейік.
Анықтама 3. {М п } нүктелер тізбегі М 0 нүктесіне жинақты деп аталады, егер кез-келген ε>0 саны үшін N 0 номері барлық n> N 0 үшін ρ(М; М 0 ) <δ теңсіздігі орындалатындай болып табылыса. Бұл жағдайда М 0 нүктесі {М п } тізбегінің шегі деп аталып,
lim М п - М 0 немесе М п →М 0 егер п→∞, деп белгіленеді.
п→∞
Анықтама 4. А саны z=f(M) фунциясының М 0 нүктесіндегі шегі деп аталады, егер М 0 нүктесіне жинақталатын кез-келген М п нүктелер тізбегі f(M 1 ), f(M 2 ), . . . , f(M п ), . . . функцияның мәндер жиыны А-ға жинақталса.
Бір айнымалылы функция үшін орындалған көптеген шек туралы қасиеттер бірнеше айнымалылы функция үшін де дұрыс болып табылатынын айта кеткен дұрыс.
Теорема 1. ƒ (М) және g (М) функциялары бір {М} жиынында анықталып М 0 нүктесіндегі шегі В және С болсын. Онда f(M) ±g(M), f(M) ۰ g(M) және f(M) /g(M) (С≠0) функцияларының М 0 нүктесінде шегі болып, сәйкес В ± С, В ۰ С және В/С болады.
Айталық, қандай да бір {М} жиынында ƒ (М) функциясы анықталып, М 0 нүктесі {М} және М 0 нүктесінің кез-келген δ -аймағы {М} жиынының барлық нүктелерін қамтысын.
Анықтама 5. z=ƒ(M) функциясы М 0 нүктесінде үздіксіз деп аталады, егер функцияның бұл нүктеде шегі болып және ол функцияның осы нүктедегі мәніне тең болса, яғни.
lim f(M) = f(M 0 ) немесе lim f(x; y) = f(x 0 ; y 0 ) .
М→ М 0 х→ х 0
у→у 0
Функцияның үздіксіздік қасиеттері орындалмайтын нүктелері функцияның үзіліс нүктелері деп аталады.
Көп айнымалылы функцияның дифференциалдануы және дербес туындылары.
z=ƒ(M) функциясы М(х; у) нүктесінің қандай да бір аймағында анықталсын. М нүктесінің х айнымалысына қалауымызша алынған Δх өсімше беріп, ал у айнымалысын өзгертусіз қалдырамыз, яғни жазықтықтың М (х; у) нүктесінен М 1 (х+ Δх; у) нүктесіне көшеміз. Сонымен қоса Δх, М нүктесі М 1 нүктесінің көрсетілген аймағында жататындай етіліп алынады. Онда функцияның сәйкес өсімшесі
Δ x z=f(x+ Δx; y) -f(x; у)
Функцияның х айнымалысы бойынша М (х; у) нүктесіндегі дербес өсімшесі деп аталады. Осыған ұқсас функцияның у айнымалысы бойынша дербес өсімшесі де келесідей анықталады
Δуz=f(x; y+ Δy) -f(x; у) .
Анықтама 1. Егер шегі
Δ x z Δуz
lim -- (lim-- )
Δх→0 Δх Δу→0
бар болса, онда ол z=ƒ(M) функциясының М нүктесіндегі х айнымалысы ( у айнымалысы) бойынша дербес туындысы деп аталады және келесі символмен белгіленеді:
z΄ x , ƒ΄ x, д²z , дƒ ( z΄ у , ƒ΄ у, д²z , дƒ ) .
дх дх ( дх дх )
Анықтама 2. z=ƒ(M) функциясының М(х; у) нүктесіндегі, х және у айнымалыларының сәйкес Δх және Δу өсімшелеріне қатысты толық өсімшесі деп Δz=ƒ(x+Δx; y+Δy) -ƒ(x; y) функциясын айтады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz