Тізбек және тізбектің шегі: анықтамалар, маңайлар және дәлелдемелер


Курстық жұмыс
Тақырыбы: Тізбек және тізбектің шегі
Мазмұны
Кіріспе . . .
1 Тізбек теориясы . . .
1. 1 Тізбектің анықтамасы, белгілеуі және берілу тәсілдері . . .
1. 2 Тізбектің шегінің анықтамасы . . .
2 Тізбек және тізбектің шегі . . .
2. 1 Тізбектің шегіне ұмтылуының кейбір мысалдары . . .
2. 2 Маңайлардың анықтамасы . . .
2. 3 Тізбектің шегінің жалпы анықтамасы . . .
2. 4 Кейбір маңызды тізбектердің шектері . . .
2. 5 Шектің анықтамасын қарама-қарсы тұжырымдау . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
Қосымша . . .
3
4
4
5
7
7
9
11
12
16
20
21
22
Кіріспе
Тізбек деп барлық оң бүтін сандар жиынында анықталған f функциясын атайды.
f
функциясының
п
оң бүтін санына сәйкес мәнін
х
п
деп белгілейді, яғни

Функция ұғымының ерекше жағдайы - тізбек - математиканың негізгі ұғымдарының бірі. Ол жиі қолданылатын болғандықтан жиі де жазылады. Сондықтан тізбекті белгілеуге ең үнемді символ
х
п
(функцияның аргументі n-ді мәні
х
п
-нің төменгі индексі түрінде жазу) ертеден пайдаланылып келеді. Оның бір себебі
х
п
жазылуы
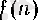 жазылуына қарағанда екі жақшаға ықшам болуымен қатар, ыңғайлы да.
жазылуына қарағанда екі жақшаға ықшам болуымен қатар, ыңғайлы да.
Курстық жұмыстың мақсаты: тізбек және тізбектің шегін зерттеу.
Міндеттері:
- тізбек теориясын қарастырып отырып, тізбектің анықтамасы, белгілеуі және берілу тәсілдерін зерттеу;
- тізбектің шегінің анықтамасын ашу;
- тізбектің шегіне ұмтылуының кейбір мысалдарын қарастыру;
- маңайлардың анықтамасын беру;
- тізбектің шегінің жалпы анықтамасын, кейбір маңызды тізбектердің шектерін қарастыру;
- шектің анықтамасын қарама-қарсы тұжырымдауын зерттеу.
Курстық жұмыстың құрамына кіріспе, екі тарау, қаорытынды мен қолданылған әдебиеттер тізімі кіреді.
1 Тізбек теориясы
1. 1 Тізбектің анықтамасы, белгілеуі және берілу тәсілдері
Тізбектің мәнін, яғни әрбір х п санын, тізбектің мүшесі дейді.
Ілгеріде ыңғайымызға қарай тізбекті мына символдармен белгілейміз:
(1)
Егер бұл жаңылушылыққа әкелмесе, онда
 тізбегі» дегеннін, орнына қысқаша
«х
п
тізбегі» дейміз.
тізбегі» дегеннін, орнына қысқаша
«х
п
тізбегі» дейміз.
Әрине,
х
-тің орнына басқа да әріптер қолданылады (мысалы,
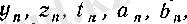 т. б. ) . Дәл солай, тізбектің аргументін n-нен басқа
т. б. ) . Дәл солай, тізбектің аргументін n-нен басқа
 әріптерімен белгілесек те ештеңе өзгермейді. Мысалы,
әріптерімен белгілесек те ештеңе өзгермейді. Мысалы,
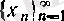 мен
мен
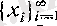 - екеуі де мына бір тізбектің белгілеуі болады:
х
1
, х
2
, . . .
- екеуі де мына бір тізбектің белгілеуі болады:
х
1
, х
2
, . . .
Тізбекті жалпы қарастырғанда немесе тізбектің анықтамасындағы сәйкестік айқын түрде емес, қанағаттандырылатын қасиеттері арқылы берілсе (мысалы, келешекте анықталатын жинақталу, монотонды т. б. қасиеттер), онда (1) белгілеулері қолданылады. Ал тізбектің анықтамасындағы сәйкестікті айқын түрде көрсету қажет болғанда, көбінесе келесі тәсілдерді пайдаланады:
1°. х п - ді тікелей табу ережесі беріледі; Мысалы, х п = 1 ( п =1, 2, . . . ) ; х п =п 2 + 4п + 3 (п=1, 2, . . . ) ; х п = п ( п =1, 2, . . . ) ; т. б.
2°. х п -ді жанама жолмен табу ережесі беріледі; Мысалы,
 (2)
(2)
яғни 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . - бұл Фибоначчи тізбегі.
Белгілі бір
k
оң бүтін саны үшін тізбектің n-ші
(n =
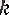 +1,
+1,
 + 2,
. . . ) мүшесін тура алдындағы
+ 2,
. . . ) мүшесін тура алдындағы
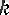 мүшелері арқылы бейнелейтін формуланы
рекуррентті
формула дейді
(recurrence
- латынша «қайтып оралатын» деген) . (2) рекуррентті формула болады (мұнда
мүшелері арқылы бейнелейтін формуланы
рекуррентті
формула дейді
(recurrence
- латынша «қайтып оралатын» деген) . (2) рекуррентті формула болады (мұнда
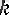 = 2) .
Осылай тізбектің рекуррентті формула арқылы анықталуы - жиі қолданылатын тәсіл.
= 2) .
Осылай тізбектің рекуррентті формула арқылы анықталуы - жиі қолданылатын тәсіл.
3°. Тізбектің мүшелерін табу ережесі сөзбен де берілуі мүмкін; Мысалы, х п - оң бүтіп сандар қатарында п-ші болып кездесетін жай сан болсын, ягни 1, 3, 5, 7, 11, . . .
4°. Алғашқы бірнеше мүшесі көрсетілгеннен, «жалпы» мүшесі де тапылады; Мысалы, тізбек 1,
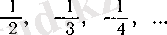 түрінде берілсе, онда жалпы мүшесі
түрінде берілсе, онда жалпы мүшесі
 болатыны айқын.
болатыны айқын.
Берілген анықтамада тізбектің мүшелерін 1 санынан бастап оң бүтін сандармен номерледік. Әрине, номерлеуді кез келген бүтін саннан (мысалы, -17, 0, 3-тен) бастасақ та ешнәрсе өзгермейді.
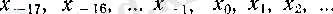 (3)
(3)
тізбегі
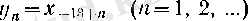 тізбегімен пара-пар, ал (3) -ші тізбектің соңғы түрде жазылуында аргументі 1-ден басталады.
тізбегімен пара-пар, ал (3) -ші тізбектің соңғы түрде жазылуында аргументі 1-ден басталады.
Осы тарауда п әрпімен тек қана оң бүтін сандарды белгілейміз. Біз келешекте осы ескертулерді арнайы атамай-ақ қолдана береміз. "*
1. 2 Тізбектің шегінің анықтамасы
Тізбек және оның шегі ұғымдары математиканың ішкі проблемаларымен қатар оны қолдану жолында пайда болады. Мысалы, біз үшбұрыштың ауданының анықтамасын және оны есептеу жолын біле тұра, радиусы R- ге тең дөңгелектің ауданы деген не және оны қалай табуға болады деген сұрақты қарастырайық.
Әрбір
 үшін радиусы
R-
ге тең дөңгелекке
үшін радиусы
R-
ге тең дөңгелекке
 бұрышты дұрыс көпбұрыш
бұрышты дұрыс көпбұрыш
 -ді іштей сызсақ, онда олардың аудандары
х
п
тізбегін құрады. Бір жағынан
п
өскен сайын
-ді іштей сызсақ, онда олардың аудандары
х
п
тізбегін құрады. Бір жағынан
п
өскен сайын
 фигурасы дөңгелекке ақырсыз жақындай түседі, екінші жағынан әрбір
п
үшін
фигурасы дөңгелекке ақырсыз жақындай түседі, екінші жағынан әрбір
п
үшін
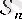 фигурасы дөңгелекпен дәл беттеспейді. Сонда дөңгелектің ауданы дегее не? Дөңгелектің ауданын неге тең деп алу керек?
фигурасы дөңгелекпен дәл беттеспейді. Сонда дөңгелектің ауданы дегее не? Дөңгелектің ауданын неге тең деп алу керек?
Осы сұрақтарға жауап беру үшін жаңа түсінік - тізбектің шегі ұғымын - енгізу керек. Шек ұғымының негізгі мағынасы мынада: Номері өскен сайын тізбектің мүшелері белгілі бір санға ақырсыз жақындайды. Сол санды тізбектің шегі деп атайды. Әрине, «номері өскен сайын мүшелері шегіне ақырсыз жақындайды» сөйлемін қандай мағынада түсінетінімізді дәл анықтауымыз қажет. Бұл келесі анықтамада беріледі.
А н ы қ т а м а.
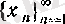 тізбегі берілсін. Егер кез келген
ɛ
оң саны арқылы барлық
тізбегі берілсін. Егер кез келген
ɛ
оң саны арқылы барлық
 үшін
үшін
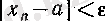 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
 саны табылса, онда
саны табылса, онда
 тізбегінің нақты мәнді шегі бар және ол
а
санына тең деп атап, оны былай белгілейді:
тізбегінің нақты мәнді шегі бар және ол
а
санына тең деп атап, оны былай белгілейді:
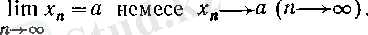 (4) ;
(4) ;
(Кейбірде, (4) белгілеулерінде
 символын қалдырып кетеміз) .
символын қалдырып кетеміз) .
Осы жағдайда
 тізбегін
«а
санына
жинақталатын
тізбек»,
«а
санына
ұмтылатын
тізбек» деп те атайды.
тізбегін
«а
санына
жинақталатын
тізбек»,
«а
санына
ұмтылатын
тізбек» деп те атайды.
Анықтамадағы
ɛ
саны туралы мынаны есте сақтаған өте пайдалы:
Бекітілген ɛ
санына оң болуынан басқа ешқандай шарт қоймай, шектің анықтамасындағы талап орындалатынын дәлелдесек, онда сол шартты
кез келген
оң
ɛ
үшін де дәлелдегеніміз болады. Расында да, анықтамадағы
ɛ
әріпі барлық оң нақты сандар жиыны R+-тi бейнелегендіктен «кез келген оң
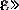 және «әрбір бекітілген оң
және «әрбір бекітілген оң
 деген сөздерінің мағынасы бір: Ол
ɛ
-ның R+-тiң барлық элементтерін бейнелеуі. Сонымен,
ɛ
әрі бекітілген, әрі кез келген оң сан. «Бекітілген» және «кез келген» сөздерінің, мағынасы қарама-қарсы болғанмен, бұл жағдайда ешқандай қайшылық жоқ.
деген сөздерінің мағынасы бір: Ол
ɛ
-ның R+-тiң барлық элементтерін бейнелеуі. Сонымен,
ɛ
әрі бекітілген, әрі кез келген оң сан. «Бекітілген» және «кез келген» сөздерінің, мағынасы қарама-қарсы болғанмен, бұл жағдайда ешқандай қайшылық жоқ.
Берілген
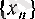 тізбсгі
а
санына ұмтылатынын немесе ұмтылмайтынын зерттегенде қандай n-дер үшін
тізбсгі
а
санына ұмтылатынын немесе ұмтылмайтынын зерттегенде қандай n-дер үшін
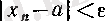 (5)
(5)
теңсіздігі орындалатынын білуіміз керек, яғни
 -ді белгісіз деп алып сол теңсіздікті шешу қажет.
-ді белгісіз деп алып сол теңсіздікті шешу қажет.
Шектің анықтамасы
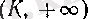 интервалындағы барлық
п
бүтін сандар (5) теңсіздігінің шешімі болатын кемінде бір
К
оң саны табылуын керек етеді. Сонымен бірге, сондай бір
К
табылса, онда одан үлкен кез келген
К
1
саны да сол шартты қанағаттандырады, себебі әрбір
интервалындағы барлық
п
бүтін сандар (5) теңсіздігінің шешімі болатын кемінде бір
К
оң саны табылуын керек етеді. Сонымен бірге, сондай бір
К
табылса, онда одан үлкен кез келген
К
1
саны да сол шартты қанағаттандырады, себебі әрбір
 үшін (5) теңсіздігі орындалса, онда (5) -тің барлық
үшін (5) теңсіздігі орындалса, онда (5) -тің барлық
 үшін де орындалуы айқын. Сондықтан,
К
1
санына көшкенде (5) теңсіздігінің
үшін де орындалуы айқын. Сондықтан,
К
1
санына көшкенде (5) теңсіздігінің
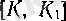 сегментіндегі шешімдері жоғалтылса да
сегментіндегі шешімдері жоғалтылса да
 сегментінің әрбір бүтін саны, сондай шешім болады),
К
1
саны шектің анықтамасындағы талапты қанағаттандырады.
сегментінің әрбір бүтін саны, сондай шешім болады),
К
1
саны шектің анықтамасындағы талапты қанағаттандырады.
Сөйтіп, бізге әдеттегідей (5) теңсіздігінің барлық шешімдерін табу қажет емес, тіпті ең кіші К -ны табу да қажет емес, өйткені (5) теңсіздігі әйтеуір бір номерден бастап (ол номер қашық па, жақын ба - бәрібір!) орындалса болғаны. Сонымен, тізбектің шегі бар екенін дәлелдеу үшін ыңғайына қарай жоғарыда айтылған көп К -ның біреуін тапсақ болғаны, өйткені бізге оның мәні емес, бар болуы маңызды. Әрине, (5) теңсіздігінің барлық шешімдер жиыны ɛ санына тәуелді, сондықтан шектің анықтамасындағы К саны да s-ға тәуелді. Осы жағдайды ескеру үшін К -ны К ɛ не К( ɛ ) деп белгілейміз.
2 Тізбек және тізбектің шегі
2. 1 Тізбектің шегіне ұмтылуының кейбір мысалдары
Келесі алты тізбектің әрқайсысының шегі бар және 0 санына тең екенін көрсетейік:
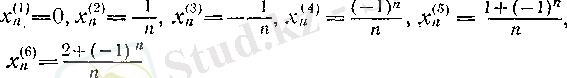
(тізбектерді бір-бірінен айыру үшін оларды жоғарғы индекс арқылы белгіледік, сонымен х -тің төменгі индексі - функциянын аргументі, жоғарғы индексі - функдияның номері) .
Қарастырылып отырған тізбектердің шегі 0 екенін кейін дәлелдейміз, қазір олар шегіне қалай ұмтылатыны туралы әсер алу үшін, алғашқы сегіз мүшесін жазайық:

Бұдан мынаны ұйғаруға болады:
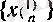 -тізбегінің мүшелерінің бәрі де шегіне (0 санына) тең, яғни мүшелері шегіне «жабысып» қалған;
-тізбегінің мүшелерінің бәрі де шегіне (0 санына) тең, яғни мүшелері шегіне «жабысып» қалған;
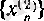 - тізбегінің мүшелерінің бәрі де шегінен үлкен;
- тізбегінің мүшелерінің бәрі де шегінен үлкен;
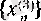 - тізбегінің мүшелерінің бәрі де шегінен кіші;
- тізбегінің мүшелерінің бәрі де шегінен кіші;
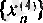 - тізбегінің мүшелері кезек-кезек шегінен үлкен және кіші;
- тізбегінің мүшелері кезек-кезек шегінен үлкен және кіші;
 - тізбегінің мүшелері кезек-кезек шегінен үлкен не оған тең:
- тізбегінің мүшелері кезек-кезек шегінен үлкен не оған тең:
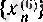 - тізбегінің мүшелері шегіне біресе жақындап, біресе алыстап ырғалып ұмтылады.
- тізбегінің мүшелері шегіне біресе жақындап, біресе алыстап ырғалып ұмтылады.
Тізбектің бірде-бір мүшесі шегіне тең болмауы мүмкін екенін ескерген жөн (мысалы,
і
= 2, 3, 4, 6 болғандағы
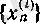 тізбектері) .
тізбектері) .
Енді ɛ оң саны берілсін (шектің анықтамасынан соң берілген түсініктеме бойынша, бұл бекітілген оң сан; бірақ осы бекітілген сан үшін керекті
 санын тапсақ онда ол кез келген оң ɛ үшін де табылды деуге болады) . Сонда біз барлық
санын тапсақ онда ол кез келген оң ɛ үшін де табылды деуге болады) . Сонда біз барлық

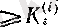 үшін
үшін
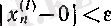 (6) .
(6) .
теңсіздігі орындалатын
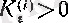 саны табылуын көрсетуіміз керек. (
саны табылуын көрсетуіміз керек. (
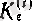 деп белгілеуіміздің себебі, әрбір тізбекке өзінің
К
ɛ
саны сәйкес) .
деп белгілеуіміздің себебі, әрбір тізбекке өзінің
К
ɛ
саны сәйкес) .
Ең алдымен
і=
1 болсын, яғни
 тізбегін қарастырайық. (6) теңсіздігіне
тізбегін қарастырайық. (6) теңсіздігіне
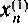 мәндерін қойып, қандай
п
үшін осы теңсіздік орындалатынын көрейік.
мәндерін қойып, қандай
п
үшін осы теңсіздік орындалатынын көрейік.
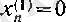 болғандықтан
болғандықтан
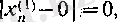 демек,
демек,
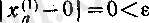 теңсіздігі кез келген
теңсіздігі кез келген
 үшін орындалады, сондықтан
үшін орындалады, сондықтан
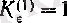 алуға болады. Сонымен,
алуға болады. Сонымен,
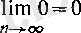 теңдігі дәлелденді.
теңдігі дәлелденді.
Енді
і
==2, 3, 4 үшін
 тецсіздігі
тецсіздігі
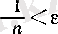 теңсіздігіне пара-пар, себебі
теңсіздігіне пара-пар, себебі

деп алуға болады. Сонымен,
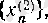
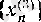 және
және
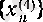 тізбектерінің шектері бар және 0 санына тең екені дәлелденді.
тізбектерінің шектері бар және 0 санына тең екені дәлелденді.
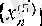 және
және
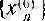 тізбектерінің шектері бар және 0 санына тең екенін дәлелдеудің алдында мынаны ескерейік.
тізбектерінің шектері бар және 0 санына тең екенін дәлелдеудің алдында мынаны ескерейік.
Егер
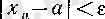 теңсіздігін тікелей шешу қиын болса, онда кейбір жағдайларда
теңсіздігін тікелей шешу қиын болса, онда кейбір жағдайларда
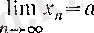 теңдігін дәлелдеу үшін
теңдігін дәлелдеу үшін
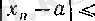 ß
n
теңсіздігі орындалатын және
ß
n
теңсіздігі орындалатын және
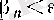 теңсіздігін
п
арқылы шешуі жеңіл болатын көмекші
теңсіздігін
п
арқылы шешуі жеңіл болатын көмекші
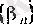 тізбегі құрылады. Әрине,
тізбегі құрылады. Әрине,
 теңсіздігінен
теңсіздігінен
 теңсіздігіне көшкенде, бірінші теңсіздіктің кейбір алғашқы шешімдерін жоғалтуымыз мүмкін, бірақ бұл, жоғарыда айтылғандай, дәлелдеуге кедергі болмайды.
теңсіздігіне көшкенде, бірінші теңсіздіктің кейбір алғашқы шешімдерін жоғалтуымыз мүмкін, бірақ бұл, жоғарыда айтылғандай, дәлелдеуге кедергі болмайды.
Мысалы, осы тәсілді
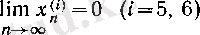 (7)
(7)
дәлелдеуіне қолданайық.

болғандықтан,
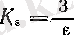 алсақ, (7) дәлелденгенін көреміз.
алсақ, (7) дәлелденгенін көреміз.
2. 2 Маңайлардың анықтамасы
Шектің анықтамасын жалпы жағдайда беру үшін өте маңызды маңайлар ұғымын келесі таблица арқылы анықтайық (мұнда ɛ оң caн) :
Кесте 2
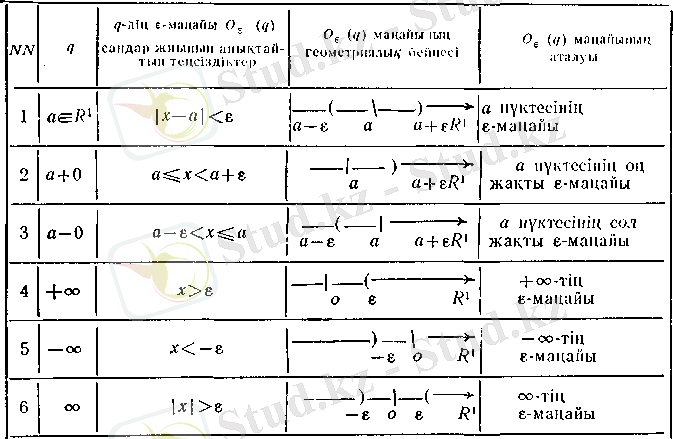
Сонымен, нақты сандар жиынында алты түрлі маңай бар.
Алғашқы үш маңайды
ақырлы
маңайлар дейді.
а
нүктесінің (нақты санының) ɛ -маңайы
а
санынан айырымының абсолют шамасы ɛ -нан кіші сандардан құралса, оң және сол жақты ɛ -маңайлары аталған жиынның
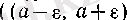 интервалының) сәйкес
а
-дан кіші емес және үлкен емес сандардан құралған. Осы жағдай
а
+ 0 және
а -
0 символдары арқылы бейнеленген (
а
+ 0 - «
а
-дан үлкен» деген) . Ақырлы маңайлар ɛ өскен сайын «кеңн» түседі, дәл айтқанда:
интервалының) сәйкес
а
-дан кіші емес және үлкен емес сандардан құралған. Осы жағдай
а
+ 0 және
а -
0 символдары арқылы бейнеленген (
а
+ 0 - «
а
-дан үлкен» деген) . Ақырлы маңайлар ɛ өскен сайын «кеңн» түседі, дәл айтқанда:
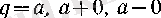 үшін:
үшін:
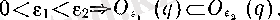
Соңғы үш маңайларды
ақырсыз
мадайлар дейді.
 және
және
 -тің ɛ- маңайлары сәйкес ɛ -нан үлкен және - ɛ- нан кіші нақты сандардан құрылса,
-тің ɛ- маңайлары сәйкес ɛ -нан үлкен және - ɛ- нан кіші нақты сандардан құрылса,
 -тің ɛ-маңайы осы екі жиынның біріктіруі болады. Ақырсыз маңайлар ɛ өскен сайын «тарыла» береді, дәл айтқанда:
-тің ɛ-маңайы осы екі жиынның біріктіруі болады. Ақырсыз маңайлар ɛ өскен сайын «тарыла» береді, дәл айтқанда:
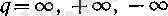 үшін
үшін
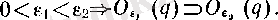
Ілгеріде
q
әріпін тек қана осы алты жағдайды белгілеуге пайдаланамыз.
q
символып
«q
нүктесі», тіпті қысқаша «
q
-да», «ɛ-дің» деп те атаймыз. Мысалы, «
q
-дің ɛ -маңайы». Кейбір жағдайларда «
q
-дің ɛ - маңайы» деудің орнына «
q
-дің маңайы» дейміз де, оны келесі мағынада түсінеміз: сөз болып отырған жиын белгілі бір ɛ үшін
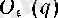 жиынына тең. Мысалы, «
А
жиыны
а
нүктесінің оң жақты мадайы» дегеніміз, белгілі бір
жиынына тең. Мысалы, «
А
жиыны
а
нүктесінің оң жақты мадайы» дегеніміз, белгілі бір
 саны үшін
саны үшін
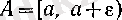 жиындар теңдігі орындалуымен пара-пар. Дәл солай,
«А
жиыны
жиындар теңдігі орындалуымен пара-пар. Дәл солай,
«А
жиыны
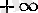 -тің маңайы» дегеніміз белгілі бір
-тің маңайы» дегеніміз белгілі бір
 саны үшін
саны үшін
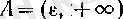 жиындар теңдігі орындалуымен пара-пар.
жиындар теңдігі орындалуымен пара-пар.
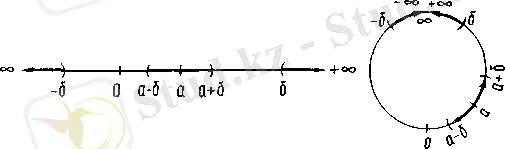
6-сурет,
Ескертулер.
1
0
. Маңайлардың ақырлы нүктелер (нақты сандар) үшін берілген анықтамаларының ақырсыз нуктелер
 үшін берілген анықтамаларынан өзгешелігі байқалады. Егер сандар түзуі 6-суретте көрсетілгендсй ойша иілген болса, онда ақырлы және ақырсыз нүктелерінің маңайларының бір түрлі анықтамасын былай беруге болады:
үшін берілген анықтамаларынан өзгешелігі байқалады. Егер сандар түзуі 6-суретте көрсетілгендсй ойша иілген болса, онда ақырлы және ақырсыз нүктелерінің маңайларының бір түрлі анықтамасын былай беруге болады:
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz