Тізбекшелер мен дербес шектер: анықтамалар, негізгі қасиеттер, Больцано-Вейерштрасс теоремасы мен Коши критерийі


Курстық жұмыс
Тақырыбы: Тізбекшелер мен дербес шектер
Мазмұны
Кіріспе . . .
1 Тізбек және шектер теориясы . . .
1. 1 Тізбектің анықтамасы, белгілеуі және берілу тәсілдері . . .
1. 2 Шектер және шектердің қолданылуы . . .
2 Тізбекшелер мен дербес шектер . . .
2. 1 Тізбекше мен дербес шектің анықтамалары . . .
2. 2 Дербес шектер жиынының негізгі қасиеттері . . .
2. 3 Больцано - Вейерштрасс теоремасы . . .
2. 4 Коши критерийі. .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
3
5
5
6
10
10
11
12
15
18
19
Кіріспе
Енді тізбек шегінің жалпы анықтамасын берейік.
А н ы қ т а м а.
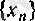 тізбегі мен 2-таблицадан алынған
q
символы берілсін. Егер әрбір ɛ оң саны арқылы барлық
тізбегі мен 2-таблицадан алынған
q
символы берілсін. Егер әрбір ɛ оң саны арқылы барлық
 үшін
үшін
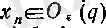 кірістіруі орындалатын
кірістіруі орындалатын
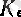 саны табылса, онда
саны табылса, онда
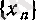 тізбегі
тізбегі
q = а болғанда, а нақты санына ұмтылады;
q = a + 0 болғанда, а санына жоғарыдан ұмтылады;
q = a- 0 болғанда, а санына төменнен ұмтылады;
болғанда,
(минус шексіздікке),
болғанда,
(плюс
шексіздікке) ұмтылады;
 болғанда,
болғанда,
 (шексіздікке) ұмтылады дейді де, былай белгілейді:
(шексіздікке) ұмтылады дейді де, былай белгілейді:
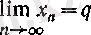 немесе
немесе
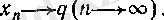 Мұнда
Мұнда
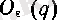 -ды, әрине, 2-таблицадан алу керек.
-ды, әрине, 2-таблицадан алу керек.
Кванторлар тілінде шектің анықтамасы былай жазылады:

Шектің жалпы анықтамасының кейбір дербес жағдайларын қарастырайық.
1°. q = a - 0 болғанда:
Егер, әрбір ɛ оң саны арқылы барлық
 үшін
а
− ɛ <
х
n
≤ a
теңсіздігі орындалатын
үшін
а
− ɛ <
х
n
≤ a
теңсіздігі орындалатын
 саны табылса, онда
саны табылса, онда
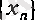 тізбегі
а
санына
тізбегі
а
санына
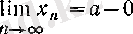
төменнен ұмтылады деп айтады да, оны былай белгілейді: немесе
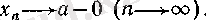
Кванторлартілінде:
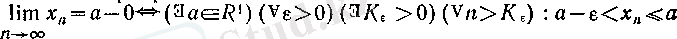
2°.
 болғанда:
болғанда:
Егер әрбір ɛ оң саны арқылы барлық
 үшін
үшін
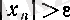 теңсіздігі орындалатын .
теңсіздігі орындалатын .
 саны табылса, онда
саны табылса, онда
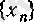 тізбегі
тізбегі
 -ке (шексіздікке) ұмтылады деп айтады да, былай белгілейді:
-ке (шексіздікке) ұмтылады деп айтады да, былай белгілейді:
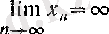 немесе
немесе
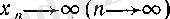
Кванторлар тілінде
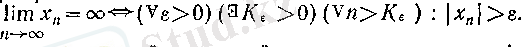
Қалған үш жағдайды осылай жазу оқырманның өзше ұсынылады (
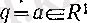 жағдайын алдында толық талқылағанбыз) .
жағдайын алдында толық талқылағанбыз) .
Курстық жұмыстың мақсаты: тізбекшелер мен дербес шектерді зерттеу.
Міндеттері:
- тізбектің анықтамасы, белгілеуі және берілу тәсілдерін қарастыру;
- шектер және шектердің қолданылуын қарастыру;
- тізбекше мен дербес шектің анықтамаларын беру;
- дербес шектер жиынының негізгі қасиеттерін зерттеу;
- Больцано - Вейерштрасс теоремасы мен Коши критерийін қарастыру.
1 Тізбек және шектер теориясы
1. 1 Тізбектің анықтамасы, белгілеуі және берілу тәсілдері
Тізбектің мәнін, яғни әрбір х п санын, тізбектің мүшесі дейді.
Ілгеріде ыңғайымызға қарай тізбекті мына символдармен белгілейміз:
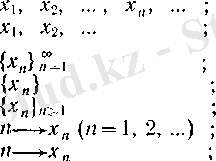 (1)
(1)
Егер бұл жаңылушылыққа әкелмесе, онда
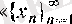 тізбегі» дегеннін, орнына қысқаша
«х
п
тізбегі» дейміз.
тізбегі» дегеннін, орнына қысқаша
«х
п
тізбегі» дейміз.
Әрине,
х
-тің орнына басқа да әріптер қолданылады (мысалы,
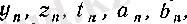 т. б. ) . Дәл солай, тізбектің аргументін n-нен басқа
т. б. ) . Дәл солай, тізбектің аргументін n-нен басқа
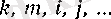 әріптерімен белгілесек те ештеңе өзгермейді. Мысалы,
әріптерімен белгілесек те ештеңе өзгермейді. Мысалы,
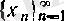 мен
мен
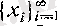 - екеуі де мына бір тізбектің белгілеуі болады:
х
1
, х
2
, . . .
- екеуі де мына бір тізбектің белгілеуі болады:
х
1
, х
2
, . . .
Тізбекті жалпы қарастырғанда немесе тізбектің анықтамасындағы сәйкестік айқын түрде емес, қанағаттандырылатын қасиеттері арқылы берілсе (мысалы, келешекте анықталатын жинақталу, монотонды т. б. қасиеттер), онда (1) белгілеулері қолданылады. Ал тізбектің анықтамасындағы сәйкестікті айқын түрде көрсету қажет болғанда, көбінесе келесі тәсілдерді пайдаланады:
1°. х п - ді тікелей табу ережесі беріледі; Мысалы, х п = 1 ( п =1, 2, . . . ) ; х п =п 2 + 4п + 3 (п=1, 2, . . . ) ; х п = п ( п =1, 2, . . . ) ; т. б.
2°. х п -ді жанама жолмен табу ережесі беріледі; Мысалы,
 (2)
(2)
яғни 1, 1, 2, 3, 5, 8, 13, 21, 34, . . . - бұл Фибоначчи тізбегі.
Белгілі бір
k
оң бүтін саны үшін тізбектің n-ші
(n =
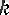 +1,
+1,
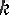 + 2,
. . . ) мүшесін тура алдындағы
+ 2,
. . . ) мүшесін тура алдындағы
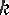 мүшелері арқылы бейнелейтін формуланы
рекуррентті
формула дейді
(recurrence
- латынша «қайтып оралатын» деген) . (2) рекуррентті формула болады (мұнда
мүшелері арқылы бейнелейтін формуланы
рекуррентті
формула дейді
(recurrence
- латынша «қайтып оралатын» деген) . (2) рекуррентті формула болады (мұнда
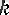 = 2) .
Осылай тізбектің рекуррентті формула арқылы анықталуы - жиі қолданылатын тәсіл.
= 2) .
Осылай тізбектің рекуррентті формула арқылы анықталуы - жиі қолданылатын тәсіл.
3°. Тізбектің мүшелерін табу ережесі сөзбен де берілуі мүмкін; Мысалы, х п - оң бүтіп сандар қатарында п-ші болып кездесетін жай сан болсын, ягни 1, 3, 5, 7, 11, . . .
4°. Алғашқы бірнеше мүшесі көрсетілгеннен, «жалпы» мүшесі де тапылады; Мысалы, тізбек 1,
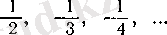 түрінде берілсе, онда жалпы мүшесі
түрінде берілсе, онда жалпы мүшесі
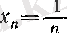 болатыны айқын.
болатыны айқын.
Берілген анықтамада тізбектің мүшелерін 1 санынан бастап оң бүтін сандармен номерледік. Әрине, номерлеуді кез келген бүтін саннан (мысалы, -17, 0, 3-тен) бастасақ та ешнәрсе өзгермейді.
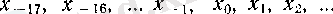 (3)
(3)
тізбегі
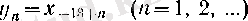 тізбегімен пара-пар, ал (3) -ші тізбектің соңғы түрде жазылуында аргументі 1-ден басталады.
тізбегімен пара-пар, ал (3) -ші тізбектің соңғы түрде жазылуында аргументі 1-ден басталады.
Осы тарауда п әрпімен тек қана оң бүтін сандарды белгілейміз. Біз келешекте осы ескертулерді арнайы атамай-ақ қолдана береміз.
1. 2 Шектер және шектердің қолданылуы
Тізбек шегі ұғымы, жалпы шек ұғымы, оқушылардың түсініп, меңгеруіне аса күрделі тақырыптардың бірі.
Тізбектің шегі бойынша функцияның шегін қалыптастыру ұзақ уақытты талап етеді, ал оқушылардың назарын аз уақытқа ғана шоғырландыруға болады. Тәуелсіз айнымалы мен тәуелді айнымалылардың ұмтылыстары екі процесс,
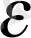 мен
мен
 -лердің тосыннан пайда болуы, шамаларының аздығы және бұлардың арасындағы сабақтастықтар бір-біріне жалғасып күрделенуінің нәтижесінде оқушылардың білім қабылдау мүмкіншіліктеріне сәйкес келмейді.
-лердің тосыннан пайда болуы, шамаларының аздығы және бұлардың арасындағы сабақтастықтар бір-біріне жалғасып күрделенуінің нәтижесінде оқушылардың білім қабылдау мүмкіншіліктеріне сәйкес келмейді.
Кесте 1
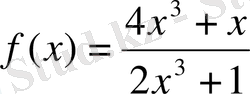
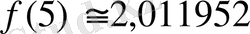
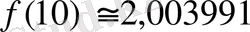
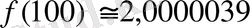
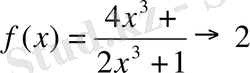
Оның үстіне «жығылғанға жұдырық» дегендей шекті есептеуге қатысты теоремалардың барлығы өте нәзік сезімді талап ететін теңсіздіктер арқылы дәлелденеді. Басқаша айтқанда, күрделенген процесті ажырату оқушылардың жақын арада даму зонасынан шығып кетуінің нәтижесінде шек ұғымы қалыптаспай келеді. Біздің ұсынып отырғанымыз процестердің саны мен ұғымды пайымдауға қажетті уақытты азайту және теңсіздікті теңдікпен ауыстыру арқылы шек ұғымын қалыптастыру ұсынылып отыр.
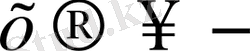 ғы шек ұғымын пайымдау әдісі. Ұғымды қалыптастыруға еңбектендіру арқылы оқушының өзін қатыстыру тиімді. Басқаша айтқанда, аталмыш ұғымды жетектеп үйрету әдісімен қалыптастыру керек. Есептеменің қарқынын жылдамдату үшін калькуляторды пайдаланған жөн.
ғы шек ұғымын пайымдау әдісі. Ұғымды қалыптастыруға еңбектендіру арқылы оқушының өзін қатыстыру тиімді. Басқаша айтқанда, аталмыш ұғымды жетектеп үйрету әдісімен қалыптастыру керек. Есептеменің қарқынын жылдамдату үшін калькуляторды пайдаланған жөн.
Осыдан кейін дербес процестерді бағанға орналастырып функциялардың шектік мәндерін жалпылау керек.

Шек ұғымының келесі проблемасы тілшелерді теңдікке алмастыру. Қосу, алу, көбейту, бөлу сияқты шек те амал. Амалдар арнайы таңбалармен белгіленеді.
Әдетте екі процесті сөзбен тұжырымдап бірден математикалық өрнегін бере салады. Мысалы, былай «шексіздікке ұмтылғанда функцияның ұмтылатын А санын оның шегі дейді және оны былай жазады»:
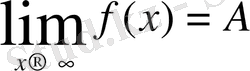
Бұл анықтама арқылы мақсатқа тез жетуге болады, бірақ процестерден осы теңдікке ауысу кезінде ашылмай қалған ұғымдар бар және шек ұғымын қалыптастыруға көру органы қатыстырылмаудың нәтижесінде оқушылардың санасында күдік сезімі қалып қояды. Күдік болған жерде ұғым қалыптасты деп айту қиын. Күдікті туғызбас үшін төменде көрсетілгендей екі-үш суретті дайындап қою керек.

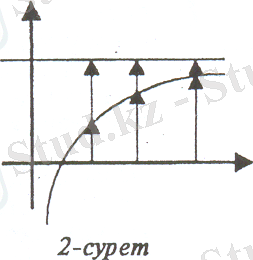
Осы суреттерде қисық сызықтардың ординаталары және функцияның шектік мәндерінің ординаталары көрсетілген. Солар арқылы мына теңдікті жазуға болады.
сурет бойынша:
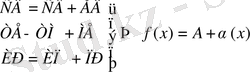
( Ш)
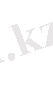 Мұндағы А тұрақты сан, ал
Мұндағы А тұрақты сан, ал
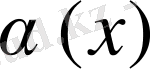 шексіз аз шама. Оның шамалары А горизонталь түзуінен жоғары орналасқан кесінділер арқылы көрсетілді. Бұл арада бір мәселеге арнайы тоқтала кетуіміз керек. Мұндағы бірінші тұрған СД, ТЕ, ИР-дің бірінші әріптері арқылы х-тің қозғалысын, ал олардың екінші әріптері арқылы тәуелді айнымалының, яғни, функцияның қозғалу кезіндегі өзгерісін көрсеттік. Суретте қанша ордината сызсақ та, оларды кесінділердің жинағы деп қарастыратын оқушылар да табылады. Олар ұзындықтары белгілі бір заңдылықпен өзгеріп қозғалып отыратын кесіндінің қалдырған іздері деген ой туғызу үшін сымның бір ұшын қисық сызық бойымен, ал екінші ұшын абцисса бойымен жылжыту арқылы функцияның графигі қозғалыстың нәтижесінде пайда болды деген сезімді оқушылардың көз алдына елестете аламыз. Графикте көрсетілмеген шексіз аз функцияның бейнесін оқушылар көз алдына елестете алмайды. Елес абстракциялық ойдың дамуына күшті әсер етеді. Вертикаль орналасқан сымның бір ұшын қисық сызықтың бойымен, ал екінші ұшын А түзуінің бойымен қозғалысқа келтіріп
шексіз аз шама. Оның шамалары А горизонталь түзуінен жоғары орналасқан кесінділер арқылы көрсетілді. Бұл арада бір мәселеге арнайы тоқтала кетуіміз керек. Мұндағы бірінші тұрған СД, ТЕ, ИР-дің бірінші әріптері арқылы х-тің қозғалысын, ал олардың екінші әріптері арқылы тәуелді айнымалының, яғни, функцияның қозғалу кезіндегі өзгерісін көрсеттік. Суретте қанша ордината сызсақ та, оларды кесінділердің жинағы деп қарастыратын оқушылар да табылады. Олар ұзындықтары белгілі бір заңдылықпен өзгеріп қозғалып отыратын кесіндінің қалдырған іздері деген ой туғызу үшін сымның бір ұшын қисық сызық бойымен, ал екінші ұшын абцисса бойымен жылжыту арқылы функцияның графигі қозғалыстың нәтижесінде пайда болды деген сезімді оқушылардың көз алдына елестете аламыз. Графикте көрсетілмеген шексіз аз функцияның бейнесін оқушылар көз алдына елестете алмайды. Елес абстракциялық ойдың дамуына күшті әсер етеді. Вертикаль орналасқан сымның бір ұшын қисық сызықтың бойымен, ал екінші ұшын А түзуінің бойымен қозғалысқа келтіріп
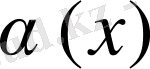 шексіз аз функция ұғымын қалыптастыруға болады. 1-ші, 2-ші суреттердің және Ш теңдігінің маңызы өте зор. Өйткені функция шектерінің модулі деп аталатын негізгі ұғымдары шектік мәнді біріктіріп отыр. Шынында да, функцияның шегін есептегенде сан, нөл және шексіздік шығады.
шексіз аз функция ұғымын қалыптастыруға болады. 1-ші, 2-ші суреттердің және Ш теңдігінің маңызы өте зор. Өйткені функция шектерінің модулі деп аталатын негізгі ұғымдары шектік мәнді біріктіріп отыр. Шынында да, функцияның шегін есептегенде сан, нөл және шексіздік шығады.
Шектік мән нөлден өзгеше сан болған жағдай үшін бірінші және екінші тамаша шектер деп аталатын формулалар енгізіледі.
Кесте 2
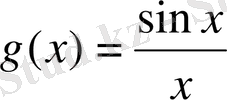
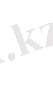
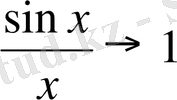
Функцияның жуық мәндерінің құрылымдарына талдау жасап алдымен е-нің мәні 2<е<3
 болатындығы туралы туралы, содан кейін е саны иррационал екендігін оқушыларға хабарлайды. Е-нің иррационалдығына мына ақпараттар негіз бола алады: «10-ның көрсеткіші өскен сайын е-нің алдыңғы жуық (көп нүктеге дейінгі) мәндеріндегі цифрлар сақталып, тағы да дәлдігін арттыратын бір цифр қосылып отырады.
болатындығы туралы туралы, содан кейін е саны иррационал екендігін оқушыларға хабарлайды. Е-нің иррационалдығына мына ақпараттар негіз бола алады: «10-ның көрсеткіші өскен сайын е-нің алдыңғы жуық (көп нүктеге дейінгі) мәндеріндегі цифрлар сақталып, тағы да дәлдігін арттыратын бір цифр қосылып отырады.
Теңдіктері канондық түрде өрнектелген нақты құрылымдардың заңдылықтары (формасы) . Бұларды формулаға айналдырмай есептемеге пайдалануға болмайды. Форманың жалпы түрі формуланы береді.
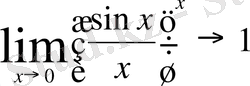
Оқушылардың қоғамға қажетті шаруашылықтың қай саласында қызмет атқаратындығы бізге беймәлім. Базарларда тұрып сауда-саттықпен айналысуыда мүмкін. Бірақ қай салада қызмет етсе де еңбегінің нәтижелі болуын көздеп олар ой таразысына салып талдайтындығы айқын. Бұл процесс. Процестің элементтерін анықтап, олардағы ақпарларды бір-бірімен салыстырып, өзгеру тенденциясына назар аударып, тиісті қорытынды жасауға үйретуге пайдаланатын оқу құралы осы шек ұғымы. Математикалық ұғымды қалыптастыру тұрғысынан қарастырғанда шек ұғымының атқаратын қызметі ерекше. Өйткені шекті есептеу кезінде математикалық формулалар мен теоремалар жиі айналымға келеді.
2 Тізбекшелер мен дербес шектер
2. 1 Тізбекше мен дербес шектің анықтамалары
Біз тізбектердің жинақталуы да, жинақталмауы да мүмкін екенін білеміз. Бұдай мынадай сұрақ туады: Барлық тізбектердің ішінде жилақталатын тізбектердің ерекшелігі неде?
Бұл сұраққа жауап «тізбекше», «дербес шек» ұғымдарын пайдалану арқылы беріледі. Сол ұғымдарды анықтайық.
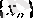 тізбегі берілсін.
тізбегі берілсін.
 (1)
(1)
теңсіздіктерін қанағаттандыратын
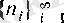 оң бүтін сандар тізбегін карастырайық (әрине,
оң бүтін сандар тізбегін карастырайық (әрине,
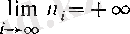 болады) .
болады) .
Егер әрбір oң бүтін
 санына
санына
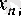 санын сәйкес қойсақ, онда бұл тәуелділік тізбек болады. Сол тізбек
санын сәйкес қойсақ, онда бұл тәуелділік тізбек болады. Сол тізбек
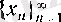 тізбегінің
тізбекшесі
деп аталады да,
тізбегінің
тізбекшесі
деп аталады да,
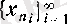 символымен белгіленеді.
символымен белгіленеді.
Сонымен, тізбекшенің өзі де тізбек болады. Ал «тізбекше» деп аталуы белгілі бір тізбектен жоғарыда айтылған әдіспен құрылғанын көрсетеді.
Әрбір тізбектің ақырсыз көп тізбекшелері бар, дәлірек айтқанда, (1) -ді қанағаттандыратын қанша
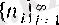 тізбектері бар болса, тізбектің сонша тізбекшесі бар болады.
тізбектері бар болса, тізбектің сонша тізбекшесі бар болады.
Тізбекшелердің ақырсыз (санаулы) жиынының мысалы ретінде мына
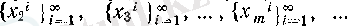 тізбекшелерді алуға болады.
тізбекшелерді алуға болады.
Тізбек пен оның тізбекшесінің арасындағы бір байланыс келесі теоремада беріледі.
Т е о р е м а. Егер
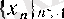 тізбегінің шегі бар және
q-
ға тең болса, онда оның кез келген тізбекшесінің де шегі бар болып, ол да
q-
ға тең болады.
тізбегінің шегі бар және
q-
ға тең болса, онда оның кез келген тізбекшесінің де шегі бар болып, ол да
q-
ға тең болады.
Дәлелдеуі.
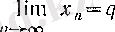 болып,
болып,
 оң саны берілсін. Онда белгілі бір номерден бастап тізбектің мүшелерінің бәрі де
q
-дың ɛ -маңайында жатады, яғни
оң саны берілсін. Онда белгілі бір номерден бастап тізбектің мүшелерінің бәрі де
q
-дың ɛ -маңайында жатады, яғни
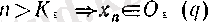 (2)
(2)
шарты орындалатын
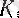 саны табылады.
саны табылады.
Енді
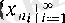 тізбекшесі берілсін (бұл бір жағынан бекітілген тізбекше; екінші жағынан,
тізбекшесі берілсін (бұл бір жағынан бекітілген тізбекше; екінші жағынан,
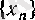 -нің тізбекшесі болатынынан өзге шарт қойылмағандықтан - кез келген тізбекше) . Әрине, (1) бойынша
-нің тізбекшесі болатынынан өзге шарт қойылмағандықтан - кез келген тізбекше) . Әрине, (1) бойынша
 теңсіздігі орындалатын
i
0
саны табылады. Соyдықтан, (2) бойынша барлық
теңсіздігі орындалатын
i
0
саны табылады. Соyдықтан, (2) бойынша барлық
 үшін
үшін
 кірістіруі орындалады, яғни
кірістіруі орындалады, яғни
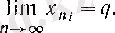
Теорема дәлелденді.
Шегі жоқ тізбекте міндетті түрде шегі жоқ тізбекше болады. Оның біреуі сол тізбектің өзі, өйткені әрбір тізбекті өзінің тізбекшесі ретінде қарастыруға болады (n i = і болғанда) .
Тізбекшінің шегін (әрине, ол бар болса) тізбектің
дербес шегі
дейді. Енді мынаны ескерейік: шектің мүмкін алты жағдайының ішінде тек қана үшеуіне - ол шек
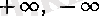 және
а
нақты caн болғанда - өзара салыстыру амалдары анықталды (бір-бірінен үлкен, тең немесе кіші болуы) .
және
а
нақты caн болғанда - өзара салыстыру амалдары анықталды (бір-бірінен үлкен, тең немесе кіші болуы) .
Ал дербес шек ұғымының ең маңызды қасиеті оларды бір-бірімен салыстыра алу мүмкіндігі болады. Сондықтан, ілгеріде дербес шек ұғымын тек қана аталған үш жағдай үшін қолданамыз.
Сонымен,
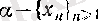 тізбегінің дербес шегі деген
a
нақты caн, +∞ немесе - ∞ болып,
тізбегінің дербес шегі деген
a
нақты caн, +∞ немесе - ∞ болып,
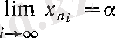 теңдігі орындалатын
теңдігі орындалатын
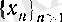 тізбегінің
тізбегінің
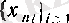 тізбекшесі табылуымен пара-пар.
тізбекшесі табылуымен пара-пар.
2. 2 Дербес шектер жиынының негізгі қасиеттері
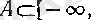
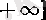 жиыны берілсін (осы пунктте жиын деп осындай жиындарды атаймыз) . Егер белгілі бір
жиыны берілсін (осы пунктте жиын деп осындай жиындарды атаймыз) . Егер белгілі бір
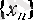 тізбегі үшін оның дербес шектер жиыны дәл осы
А
болса, онда
А
дербес шектер жиыны дейді.
тізбегі үшін оның дербес шектер жиыны дәл осы
А
болса, онда
А
дербес шектер жиыны дейді.
Дербес шектер жиынының негізгі қасиеттерін атап өтейік (олардың кейбіреулерінің дәлелдеулері кейін беріледі) .
1°. Бос жиын дербес шектер жиыны бола алмайды, яғни бірде-бір дербес шегі болмайтын тізбек жоқ (жоғарыда келісілгендей, дербес шек
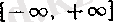 сегментінен алынады) .
сегментінен алынады) .
2°. Бір элементті жиын дербес шектер жиыны болады. Әрбір шегі бар болатын тізбектің дербес шектерінің жиыны тек қана сол шектен құрылған бір элементті жиын болады (бұны жоғарыда дәлелдедік) . Бұған кері тұжырымда орындалатынын біз төменде дәлелдейміз (3°-ді қараңыз) . Сондықтан, алдыңғы пунктте қойылған сұраққа жауап былай беріледі: тізбектің шегі бар болуы үшін оның дербес шектер жиыны бір элементті болуы қажетті және жеткілікті.
3°. Кез келген ақырлы жиын дербес шектер жиыны болады.
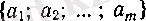 - нақты сандар жиыны берілсін. Онда
- нақты сандар жиыны берілсін. Онда
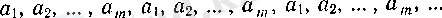 (3)
(3)
тізбегінің дербес шектер жиыны дәл сол жиын болады.
Расында да, (З) -тен әрбір
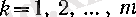 . үшін барлық мәндері
. үшін барлық мәндері
 санына тең тізбекше бар болатыны айқын. Әрине, сол тізбекшенің шегі де
санына тең тізбекше бар болатыны айқын. Әрине, сол тізбекшенің шегі де
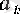 болады.
болады.
Енді (3) тізбегін аналитикалық түрде жазайық (формула арқылы) . Әрбір бүтін оң
п
санын
 1, 2 . . .
т
) түрінде тек қана бір тәсілмен бейнеленетінін пайдалансақ, онда (3) былай жазылады
1, 2 . . .
т
) түрінде тек қана бір тәсілмен бейнеленетінін пайдалансақ, онда (3) былай жазылады
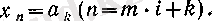 Мұнан барлық мәндері
Мұнан барлық мәндері
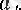 санына тең тізбекшенің мысалы
санына тең тізбекшенің мысалы
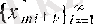 тізбегі болатынын көреміз.
тізбегі болатынын көреміз.
Дәлелдеу толық болу үшін берілген жиында жатпайтын әрбір нақты сан дербес шек бола алмайтынын көрсету қажет, оны оқырманның өзіне ұсынамыз.
Егер
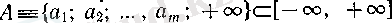 " болса
" болса

 онда
онда
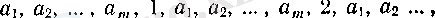
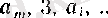 тізбегінің дербес шектер жиыны дәл
А
болады. Бұның дәлелдеуі алдыңғы жағдайдағыдай.
тізбегінің дербес шектер жиыны дәл
А
болады. Бұның дәлелдеуі алдыңғы жағдайдағыдай.
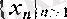 4°. Дербес шектер жиыны сегмент болуы мүмкін. Қажетті тізбегі былай құрылады:
х
1
=0. 1. x
13
=0, 13,
х
17
=
0, 17
, x
17101975
=0, 17101975 болсын, яғни әрбір оц бүтін
4°. Дербес шектер жиыны сегмент болуы мүмкін. Қажетті тізбегі былай құрылады:
х
1
=0. 1. x
13
=0, 13,
х
17
=
0, 17
, x
17101975
=0, 17101975 болсын, яғни әрбір оц бүтін
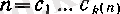 (c
1
- цифрлар) санына ондық системада жазылуына қарай
(c
1
- цифрлар) санына ондық системада жазылуына қарай
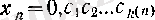 саны сәйкес қойылсын. с
1
=1, 2, . . . , 9 болғандықтан, әрбір
п
үшін
саны сәйкес қойылсын. с
1
=1, 2, . . . , 9 болғандықтан, әрбір
п
үшін
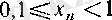 теңсіздігі орындалатыны айқын.
теңсіздігі орындалатыны айқын.
Енді
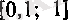 сегментіндегі әрбір нақты сантізбегінің
сегментіндегі әрбір нақты сантізбегінің
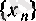 дербес шегі болатынын көрсетейік. Расында да, әрбір
[0, 1; 1] саны ондық бөлшек арқылы былай бейнеленеді:
дербес шегі болатынын көрсетейік. Расында да, әрбір
[0, 1; 1] саны ондық бөлшек арқылы былай бейнеленеді:
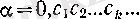 (С; - цифрлар) .
(С; - цифрлар) .
а
-ға ұмтылатын тізбекшенің мысалы
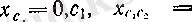
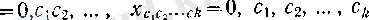 болатыны айқын.
болатыны айқын.
Мынаны ескерейік:
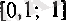 сегментінде қанша нақты сан бар болса, біз сонша тізбекше құрдық.
сегментінде қанша нақты сан бар болса, біз сонша тізбекше құрдық.
5°. Қандай интервалды алсақ та, ол дербес шектер жиыны бола алмайды (бұл төменде дәлелденетін жалпы теореманың салдары) .
2. 3 Больцано - Вейерштрасс теоремасы
Алдыңғы пунктте берген уәдемізді орындайық.
Теорема. Қез келген тізбектен кемінде бір ақырлы, әлде ақырсыз шегі бар болатын тізбекше бөліп алуға болады.
Дәлелдеуі. Дәлелдеуді тізбектің шенелуіне немесе шенелмеуіне қарай екі леммаға бөлейік.
1-Лемма. Әрбір шенелген тізбектің кемінде бір дербес шегі бар. (Әрине, ол ақырлы болады, өйткені тізбек шенелген) .
Д ә л е л д е у і.
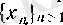 шенелген тізбегі берілсін. Онда
шенелген тізбегі берілсін. Онда
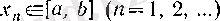 (4)
(4)
кірістіруі орындалатын
 нақты сандары табылады. Енді қажетті нақты шегі бар болатын
нақты сандары табылады. Енді қажетті нақты шегі бар болатын
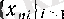 тізбекшесін құру үшін
тізбекшесін құру үшін
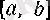 сегментінен бастап сегменттер ұясын былай анықтайық.
сегментінен бастап сегменттер ұясын былай анықтайық.
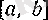 сегментін ұзындықтары тең болатын екі сегментке бөлейік:
сегментін ұзындықтары тең болатын екі сегментке бөлейік:
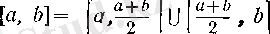 . Осы екі сегменттің кемінде біреуінде (ол
. Осы екі сегменттің кемінде біреуінде (ол
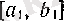 болсын) тізбектің ақырсыз көп элементтері бар, яғни кез келген
К
саны үшін
болсын) тізбектің ақырсыз көп элементтері бар, яғни кез келген
К
саны үшін
 болып,
болып,
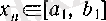 (5)
(5)
кірістіруіп қанағаттандыратын
п
саны табылады. Басқа сөзбен айтқанда, (5) кірістіруін қанағаттандыратып
п
санын қалауымызша үлкен алуға болады. Расында да, олай болмаса, яғни белгілі бір
К
саны мен кез келген
 үшін
үшін
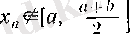 және,
және,
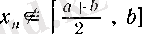 шарттары орындалса, онда барлық
шарттары орындалса, онда барлық
 үшін
үшін
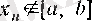 болар еді, ал бұл (4) -ке қайшы.
болар еді, ал бұл (4) -ке қайшы.
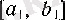 сегментінің ұзындығы
сегментінің ұзындығы
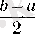 болады.
болады.
Дәл осылай,
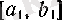 сегментін ұзындықтары тең екі сегментке бөліп, соның ішінен аталған шарттарды қанағаттандыратын
сегментін ұзындықтары тең екі сегментке бөліп, соның ішінен аталған шарттарды қанағаттандыратын
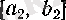 сегментін бөліп аламыз. Осылай ақырсыз жалғастыра берсек, онда
і
қадамында келесі қасиеттерді қанағаттандыратын
сегментін бөліп аламыз. Осылай ақырсыз жалғастыра берсек, онда
і
қадамында келесі қасиеттерді қанағаттандыратын
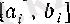 сегменті бөлінеді:
а)
сегменті бөлінеді:
а)
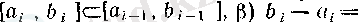
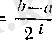 ,
,
 кірістіруін қанағаттандыратып
п
санын қалауымызша үлкен алуға болады.
а)
қасиетінен әрбір
кірістіруін қанағаттандыратып
п
санын қалауымызша үлкен алуға болады.
а)
қасиетінен әрбір
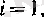 2, . . . үшін
2, . . . үшін
 теңсіздіктері орындалатынын көреміз, демек, сол сегменттердің шеткі нүктелерінен құрылған
теңсіздіктері орындалатынын көреміз, демек, сол сегменттердің шеткі нүктелерінен құрылған
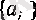 және
және
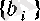 тізбектері сәйкес кемімейтін және өспейтін болады.
тізбектері сәйкес кемімейтін және өспейтін болады.
 ) қасиетінен
) қасиетінен
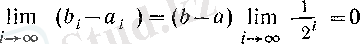 теңдігі шығады.
теңдігі шығады.
Сондықтан 6 (§ 3) -пункттегі теорема бойынша
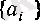 және
және
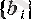 тізбектерінің нақты мәнді шектері бар болып, өзара тең болады:
тізбектерінің нақты мәнді шектері бар болып, өзара тең болады:
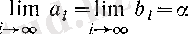 (6)
(6)
Сол екі шектің ортақ мәні
а
әрпімен белгілемген. Енді бізге қажетті тізбекшені индукция тәсілін қолданып, былай құрамыз:
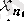 ретінде
ретінде
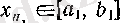 кірістіруін қанағаттандыратып элементтің кез келгенін алуға болады (бұл
кірістіруін қанағаттандыратып элементтің кез келгенін алуға болады (бұл
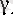 ) бойынша мүмкін) ; .
) бойынша мүмкін) ; .
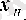 ретінде
ретінде
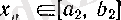 және
және
 шарттарып қанағаттандыратын элементтің біреуін алайық (бұл
шарттарып қанағаттандыратын элементтің біреуін алайық (бұл
 ) бойынша мүмкін) . Дәл осылай ақырсыз жалғастыра берсек, онда
) бойынша мүмкін) . Дәл осылай ақырсыз жалғастыра берсек, онда
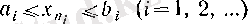 (7)
(7)
теңсіздіктерін қанағаттандыратын
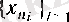 тізбекшесі құрылады. (6) және (7) -ден 3 (§ 2) -пункттегі 6-теорема бойынша
тізбекшесі құрылады. (6) және (7) -ден 3 (§ 2) -пункттегі 6-теорема бойынша
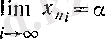 теңдігі орындалады, яғни
теңдігі орындалады, яғни
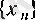 тізбегінің дербес нақты мәнді шегі бар болады. 1-лемма толық дәлелденді.
тізбегінің дербес нақты мәнді шегі бар болады. 1-лемма толық дәлелденді.
2-лемма.
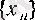 тізбегі берілсіп. Егер
тізбегі берілсіп. Егер
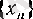 тізбегі жоғарыдан (төменнен) шенелмесе, онда
тізбегі жоғарыдан (төменнен) шенелмесе, онда
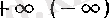 оның дербес шегі болады.
оның дербес шегі болады.
Дәлелдеуі. Анықтық үшін
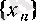 тізбегі жоғарыдан шенелмеген болсын. Бізге
тізбегі жоғарыдан шенелмеген болсын. Бізге
 -ке ұмтылатын тізбекше құру керек. Ол үшін әрбір оң бүтін
і
саны үшін
-ке ұмтылатын тізбекше құру керек. Ол үшін әрбір оң бүтін
і
саны үшін
 (8) теңсіздігін қанағаттандыратын
(8) теңсіздігін қанағаттандыратын
 (9)
(9)
оң бүтін сандар тізбегін құрсақ болғаны, өйткені (8) -ден
 тізбекшесінің
тізбекшесінің
 -ке ұмтылуы айқын. Енді сол тізбекшені құрайық.
-ке ұмтылуы айқын. Енді сол тізбекшені құрайық.
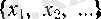 сандар жиыны жоғарыдан шенелмегендіктен
,
онда 1 санынан үлкен
сандар жиыны жоғарыдан шенелмегендіктен
,
онда 1 санынан үлкен
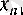 элементі бар болады.
элементі бар болады.
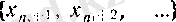 сандар жиыны жоғарыдан шенелмеген болады (2 (§ 2) -пункттегі 4°-ді қараңыз), демек, онда 2 санынан үлкен
сандар жиыны жоғарыдан шенелмеген болады (2 (§ 2) -пункттегі 4°-ді қараңыз), демек, онда 2 санынан үлкен
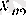 элементі бар болады және
элементі бар болады және
 (себебі
(себебі
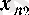 алынған жиынның элементтерінің номерлері
алынған жиынның элементтерінің номерлері
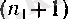 -ден басталады!) .
-ден басталады!) .
(8) - (9) шарттарын қанағаттандыратын тізбекшенің құрылуы индукция тәсілі арқылы былай аяқталады:
Егер
 үшін
үшін
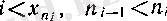 болса, онда
болса, онда
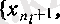
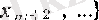 жиыны жоғарыдан шенелмеген болғандықтан, сол жиында
жиыны жоғарыдан шенелмеген болғандықтан, сол жиында
 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
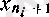 элементі бар болады. Әрине,
элементі бар болады. Әрине,
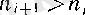 теңсіздігі де орындалады.
теңсіздігі де орындалады.
Лемма, сонымен бірге теорема да, толық дәлелденді.
Е с к е р т у. Кейбірде Больцано - Вейерштрасс теоремасы деп 1-лемманы атайды. Бұның себебі мынада: 2-лемманың дәлелденуінде тек қана тізбектің шегі мен шенелмегендігінің анықтамасын пайдаландық. Ал 1-леммада өте терең қасиет берілген, оның дәлелденуінде нақты сандар жиынының негізгі қасиеті- монотонды тізбектің шегі бар болатыны - міндетті түрде пайдаланылуы керек.
2. 4 Коши критерийі
Біз тізбектің жинақталуының бір жеткілікті (бірақ қажетті емес) шарттарымен таныспыз - ол тізбектің монотонды және шенелген болуы. Ал жалпы жағдайда не айтуға болады? Дәл айтқанда, берілген
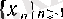 тізбегінің тек қана анықтамасындағы сәйкестікті пайдаланып жинақталатынын, не жинақталмайтынын білуге бола ма?
тізбегінің тек қана анықтамасындағы сәйкестікті пайдаланып жинақталатынын, не жинақталмайтынын білуге бола ма?
Бұл сұраққа жауапты Коши критерийі береді, бірақ оны келтіру үшін бізге алдын ала келесі анықтама қажет.
Анықтама.
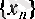 тізбегі берілсін. Егер әрбір
е
оң саны арқылы
тізбегі берілсін. Егер әрбір
е
оң саны арқылы
 және
және
 теңсіздіктерін қанағаттандыратын кез келген оң бүтін
п
және
т
сандары үшін
теңсіздіктерін қанағаттандыратын кез келген оң бүтін
п
және
т
сандары үшін
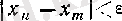 шарты орындалатын
шарты орындалатын
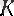 саны табылса, онда
саны табылса, онда
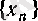 тізбегі
Коши тізбегі,
мұндағы шарт
Коши шарты
деп аталады.
тізбегі
Коши тізбегі,
мұндағы шарт
Коши шарты
деп аталады.
Кванторлар тілінде Коши шарты былай жазылады:
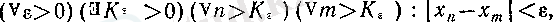
сондықтан, Коши шартының орындалмауы мынау болады:

яғни, сөзбен айтқанда: Белгілі бір
е
оң саны үшін қандай
К
оң санын алсақ та, номерлері
К
-дан үлкен, ал мәндерінің арақашықтығы
е
-нан кем болмайтын тізбектің екі мүшесі бар болады. 2 (I тарау, § 1) -пунктте айтылғандай, «критерий» сөзін «қажетті және жеткілікті» деген мағынада қолданамыз, яғни критерин деген теорема және сол теореманың түрі
 болады. Басқаша айтқанда,
А
және
В
тұжырымдары екеуі де қатар орындалады немесе екеуі де қатар орындалмайды.
болады. Басқаша айтқанда,
А
және
В
тұжырымдары екеуі де қатар орындалады немесе екеуі де қатар орындалмайды.
Коши к р и т е р и й і. 1 0 . Жинақталатын тізбек Коши тізбегі болады. 2°. Коши тізбегі жинақталатын тізбек болады.
Басқа сөзбен айтқанда, берілген
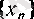 тізбегінің нақты мәнді шегі бар болуы үшін, ол Коши шартын қанағаттандыруы қажетті және жеткілікті.
тізбегінің нақты мәнді шегі бар болуы үшін, ол Коши шартын қанағаттандыруы қажетті және жеткілікті.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz