Үзіліссіз функциялардың локальды қасиеттері және элементар функциялардың үзіліссіздігі


Курстық жұмыс
Тақырыбы: Үзіліссіз функциялардың локальды қасиеттері. Элементар функциялардың үзіліссіздігі
Мазмұны
Кіріспе . . .
1 Үзіліссіз функциялар теориясы . . .
1. 1 Функцияның үзіліссіздігі . . .
1. 2 Функция үзіліссіздігінің негізгі теоремалары . . .
1. 3 Функция үзіліссіздігінің қасиеттері . . .
2 Үзіліссіз функциялардың локальды қасиеттері. Элементар функциялардың үзіліссіздігі . . .
2. 1 Үзіліссіз функциялардың кейбір локальды қасиеттері . . .
2. 2 Элементар функциялардың үзіліссіздігі . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
Қосымша . . .
3
5
5
6
8
12
12
13
16
17
18
Кіріспе
Айталық f(x) функциясы Х сан жиынында анықталсын.
анықтама. Егер f(x) функциясының
 нүктесінде шегі бар болып, ол f(x) функциясының сол нүктедегі мәні f(x0) -ге тең болса, онда f(x) функциясын х0 нүктесінде үзіліссіз деп атайды.
нүктесінде шегі бар болып, ол f(x) функциясының сол нүктедегі мәні f(x0) -ге тең болса, онда f(x) функциясын х0 нүктесінде үзіліссіз деп атайды.
Бұл анықтаманы үзіліссіздіктің формальды анықтамасы дейді.
Функция үзіліссіз болатын нүктені үзіліссіздік нүктесі дейді.
анықтама. (Гейне) . Егер Х жиынынан алынған кез келген х1, х2, . . . , хn, . . тізбегі х0 санына жинақты болғанда осы тізбекке сәйкес келетін f(x1), f(x2) …, f(xn) …тізбегі f(x0) санына жинақты болса, онда f(x) функциясын х0 нүктесінде үзіліссіз дейді.
анықтама. (Коши) . Егер кез келген
 санына сәйкес
санына сәйкес

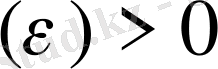 саны табылып
саны табылып
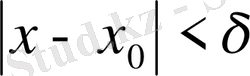
теңсіздігін қанағаттандыратын х-тің барлық мәндері үшін
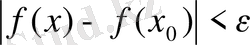
теңсіздігі орындалса, онда f(x) функциясын х0 нүктесінде үзіліссіз деп атайды. Оны
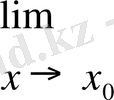
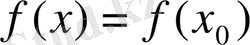 жазады.
жазады.
Енді
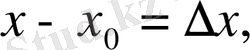 ал сәйкес келетін функция өсімшесін
ал сәйкес келетін функция өсімшесін
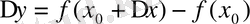 деп белгілейміз.
деп белгілейміз.
Егер х0 нүктесіндегі аргументтің шексіз аз өсімшесіне функцияның шексіз аз өсімшесі сәйкес келсе, онда y=f(x) функциясын х0 нүктесінде үзіліссіз деп атайды да былай жазады:
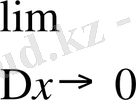
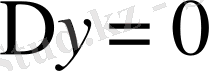
Егер y=f(x) функциясы Х сан жиынының әрбір нүктесінде үзіліссіз болса, онда f(x) функциясын Х жиынында үзіліссіз деп атайды.
Егер х0 нүктесінде f(x) функциясы үзіліссіз болмаса, онда х0 нүктесін f(x) функциясының үзіліс нүктесі деп атайды, ал функцияның өзін осы нүктеде үзілісті дейді.
Егер f(x) функциясы х0 нүктесінде үзіліссіз болса, онда
f(x0+0) =f(x0-0) =f(x0) орындалатыны белгілі.
Егер f(x0+0) және f(x0-0) шекті шектер бар, бірақ ол f(x0) - ден өзгеше болса, онда х0 нүктесін бірінші текті үзіліс нүкте деп атайды.
f(x0+0) -f(x0-0) - айырмасын f(x) функциясының х0 нүктесіндегі “секірісі” деп атайды.
Егер
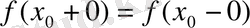
 болса, онда х0 нүктесін жойылатын үзіліс нүкте деп атайды.
болса, онда х0 нүктесін жойылатын үзіліс нүкте деп атайды.
Егер оң немесе сол жақты шектердің жоқ дегенде біреуі болмаса, онда х0 нүктесін f(x) функциясының екінші текті үзіліс нүктесі дейді.
Больцано- Кошидің бірінші теоремасы.
f(x) функциясы
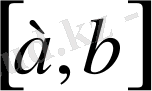 кесіндісінде үзіліссіз және кесіндінің ұштарында функция мәндерінің таңбалары әр түрлі болса, онда
кесіндісінде үзіліссіз және кесіндінің ұштарында функция мәндерінің таңбалары әр түрлі болса, онда
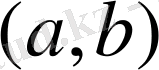 аралығында ең болмаса бір нүкте
аралығында ең болмаса бір нүкте
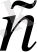 табылып, f(c) =0 болады.
табылып, f(c) =0 болады.
Больцано- Кошидің екінші теоремасы.
Егер f(x) функциясы
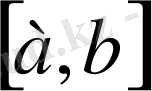 кесіндісінде үзіліссіз және
кесіндісінде үзіліссіз және
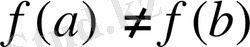 болса, онда функция осы сегментте
болса, онда функция осы сегментте
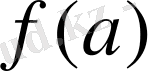 мен
мен
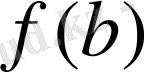 сандарының арасында жатқан кез келген
сандарының арасында жатқан кез келген
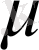 мәнін қабылдайды, демек
мәнін қабылдайды, демек
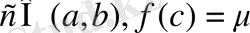 теңдігін қанағаттандыратын кемінде бір с саны табылады.
теңдігін қанағаттандыратын кемінде бір с саны табылады.
Вейерштрасстың 1-теоремасы.
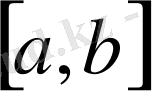 кесіндісінде үзіліссіз f(x) функциясы осы кесіндіде шектелген.
кесіндісінде үзіліссіз f(x) функциясы осы кесіндіде шектелген.
Вейерштрасстың 2-теоремасы. Егер
 функциясы
функциясы
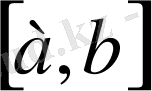 кесіндісінде үзіліссіз болса, онда осы сегментте функция өзінің дәл төменгі және дәл жоғарғы шекараларын қабылдайды, демек х1, х2,
кесіндісінде үзіліссіз болса, онда осы сегментте функция өзінің дәл төменгі және дәл жоғарғы шекараларын қабылдайды, демек х1, х2,
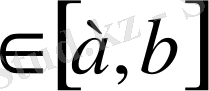 нүктелер табылып
нүктелер табылып
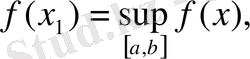
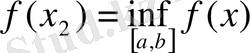
Курстық жұмыстың мақсаты: Үзіліссіз функциялардың локальды қасиеттерін ашу, элементар функциялардың үзіліссіздігін зерттеу.
1 Үзіліссіз функциялар теориясы
1. 1 Функцияның үзіліссіздігі
Қандай да бір
х
о
нүктесі мен центрі
х
q
нүктесі болатын қандай да бір аймақта анықталған, яғни
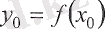 теңдігі орындалатын
теңдігі орындалатын
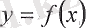 функцияеын қарастырамыз.
функцияеын қарастырамыз.
Егер х айнымалысына қандайда бір оң немесе теріс
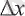 өсімшесін берсек және
өсімшесін берсек және
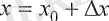 мәнін қабылдайтын болсын, онда
у
функциясы да қандай да бір
мәнін қабылдайтын болсын, онда
у
функциясы да қандай да бір
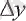 өсімшесін қабылдайды. Функцияның жаңа өсірілген мәні мына түрде анықталады
өсімшесін қабылдайды. Функцияның жаңа өсірілген мәні мына түрде анықталады
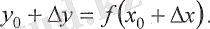 (4. 2)
(4. 2)
Бұл тендеуден
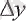 есімшесі келесі формула аркылы өрнектеледі (6-сурет)
есімшесі келесі формула аркылы өрнектеледі (6-сурет)
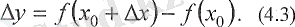
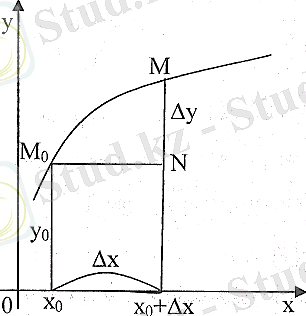
6-сурет
9-анықтама. Егер ол х о нүктесінде және оның қандай да бір аймағында анықталған және
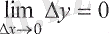 (4. 4)
(4. 4)
Немесе
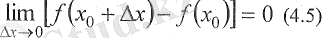
болса, онда
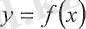 функциясы
х= х
0
мәнінде (нүктесінде)
үзіліссіз (үздіксіз)
деп аталады.
функциясы
х= х
0
мәнінде (нүктесінде)
үзіліссіз (үздіксіз)
деп аталады.
Үзіліссіздіктің соңғы шартын, яғни (4. 5) теңдігін мына түрде жазуға да болады:
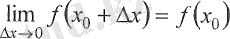 (4. 6)
(4. 6)
Немесе
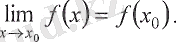 (4. 7)
(4. 7)
Енді
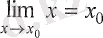 болатынын ескеретін болсақ, онда (4. 7) теңдеуді келесі түрде жазамыз:
болатынын ескеретін болсақ, онда (4. 7) теңдеуді келесі түрде жазамыз:
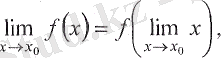 (4. 8)
(4. 8)
яғни үздіксіз функцияның
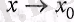 ұмтылғандағы шегін табу үшін функция өрнегіндегі
х
аргументінің орнына х
0
мәнін қою жеткілікті болады.
ұмтылғандағы шегін табу үшін функция өрнегіндегі
х
аргументінің орнына х
0
мәнін қою жеткілікті болады.
Геометриялық тұрғыдан қарағанда функцияның нүктедегі үзіліссіздігі дегеніміз, егер
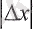 өте аз болғанда
өте аз болғанда
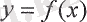 функциясының графигінің
функциясының графигінің
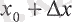 және х
0
нүктелеріндегі ординаталарының айырмасы абсолют шамасы бойынша өте аз шама болады.
және х
0
нүктелеріндегі ординаталарының айырмасы абсолют шамасы бойынша өте аз шама болады.
Мысалы, у = х функциясының кез келген х 0 нүктесінде үзіліссіздігін есептейміз.
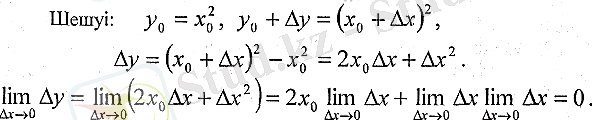
1. 2 Функция үзіліссіздігінің негізгі теоремалары
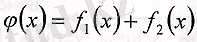 1-теорема.
Егер
1-теорема.
Егер
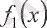 ' және
' және
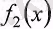 функциялары
х
0
нүктесінде үзіліссіз болса, онда қосынды функциясы да
х
0
нүктесінде үзіліссіз болады.
функциялары
х
0
нүктесінде үзіліссіз болса, онда қосынды функциясы да
х
0
нүктесінде үзіліссіз болады.
Дәлелдеу: Теореманың шарты бойынша
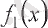 және
және
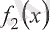 функциялары үзіліссіз болғандықтан (4. 7) теңдеуінің негізінде, келесі түрде жазуға болады
функциялары үзіліссіз болғандықтан (4. 7) теңдеуінің негізінде, келесі түрде жазуға болады
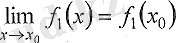 және
және
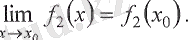
Шектер теориясының негізінде
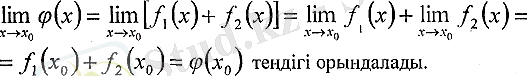
Сонымен,
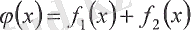 қосындысы үзіліссіз функция болады.
қосындысы үзіліссіз функция болады.
Шектердің негізі қасиеттеріне сүйене отырып, төмендегі теоремаларды да дәлелдеуге болады.
2-теорема. Екі үзіліссіз фукциялардың кебейтіндісі де үзіліссіз функция боладьт.
3-теорема. Екі үзіліссіз функциялардың қатынасы да үзіліссіз функция болады, егер бөліміндегі функция нөлге тең емес болса.
4-теорема.
Егер
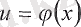 функциясы
х
=
х
о
нүктесінде үзіліссіз жэне
функциясы
х
=
х
о
нүктесінде үзіліссіз жэне
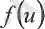 функциясы
функциясы
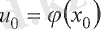 нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда
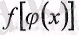 функциясы
х
0
нүктесінде үзіліссіз функция болады.
функциясы
х
0
нүктесінде үзіліссіз функция болады.
5-теорема. Барлық элементарлық функциялар өздерінің анықталу облысында үзіліссіз болады.
10-анықтама.
Егер
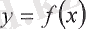 фукциясы
фукциясы
 болған кезде
(a, b)
интервалының әр бір нүктесінде үзіліссіз болса, онда функция осы интервалда үзіліссіз болады.
болған кезде
(a, b)
интервалының әр бір нүктесінде үзіліссіз болса, онда функция осы интервалда үзіліссіз болады.
11
-анықтама.
Егер
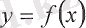 функциясы
х = а
анықталған және
функциясы
х = а
анықталған және
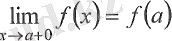 болса, онда
х = а
нүктесінде
оң жағынан үзіліссіз
деп аталады.
болса, онда
х = а
нүктесінде
оң жағынан үзіліссіз
деп аталады.
12
-анықтама.
Егер
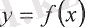 функциясы
х - b
анықталған және
функциясы
х - b
анықталған және
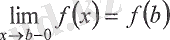 болса, онда
х = b
нүктесінде
сол жағынан үзіліссіз
деп аталады.
болса, онда
х = b
нүктесінде
сол жағынан үзіліссіз
деп аталады.
13-анықтама.
Егер
 функциясы
(а, b)
интервалының әрбір нүктесінде және шеткі нүктелерінде сәйкес оң жағынан және сол жағынан үзіліссіз болса, онда
функциясы
(а, b)
интервалының әрбір нүктесінде және шеткі нүктелерінде сәйкес оң жағынан және сол жағынан үзіліссіз болса, онда
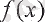 функциясы
тұйықталған интервалда
немесе
функциясы
тұйықталған интервалда
немесе
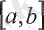 кесіндісінде үзіліссіз
деп аталады.
кесіндісінде үзіліссіз
деп аталады.
14-анықтама.
Егер қандай да бір
х - х
0
нүктесінде
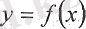 функциясы үшін үзіліссіздіктің ең кемінде бір шарты орындалмаса, яғни
функциясы үшін үзіліссіздіктің ең кемінде бір шарты орындалмаса, яғни
 болған кезде функция анықталмаған немесе
болған кезде функция анықталмаған немесе
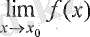 шегі болмаса немесе
шегі болмаса немесе
 кез келген ұмтылғанда
кез келген ұмтылғанда
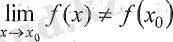 болса, бірақ теңдіктің оң жағындағы және сол жағындағы ернектердің мәні бар болса, онда
болса, бірақ теңдіктің оң жағындағы және сол жағындағы ернектердің мәні бар болса, онда
 функциясы
функциясы
 нүктесінде үзілісті (үздікті)
деп аталады.
нүктесінде үзілісті (үздікті)
деп аталады.
15-анықтама.
Егер функциясының
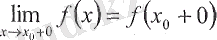 және
және
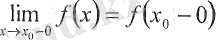 ақырлы шектері бар, бірақ
ақырлы шектері бар, бірақ
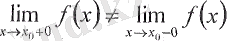 немесе
немесе
 нүктесінде
нүктесінде
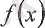 функциясының мәні болмаса, онда
функциясының мәні болмаса, онда
 нүктесі
І-ші тектегі
үзілістік нүктесі болады.
нүктесі
І-ші тектегі
үзілістік нүктесі болады.
16-анықтама.
Егер
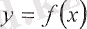 функциясының
функциясының
 нүктесінде
нүктесінде
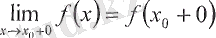 немесе
немесе
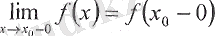 шектері жоқ немесе шексіздікке тең болса, онда
шектері жоқ немесе шексіздікке тең болса, онда
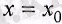 нүктесі
ІІ-ші тектегі
үзілістік нүктесі болады.
нүктесі
ІІ-ші тектегі
үзілістік нүктесі болады.
1. 3 Функция үзіліссіздігінің қасиеттері
Бұл бөлімде кесіндідегі үзіліссіз функциялардың кейбір қасиетгерін қарастырамыз.
6-теорема.
Егер
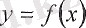 функциясы қандайда бір
функциясы қандайда бір
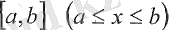 кесіндісінде үзіліссіз болса, онда
кесіндісінде үзіліссіз болса, онда
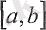 кесіндісінде ең кемінде
кесіндісінде ең кемінде
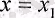 бір нүктесі табылып, функцияның осы нүктедегі мәндері мына теңсіздікті қанағаттандырады
бір нүктесі табылып, функцияның осы нүктедегі мәндері мына теңсіздікті қанағаттандырады
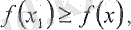
мұндағы
х -
кесіндінің кез келген басқа нүктесі және ең кемінде
 бір нүктесі табылып, функцияның осы нүктедегі мәндері мына теңсіздікті қанағаттандырады
бір нүктесі табылып, функцияның осы нүктедегі мәндері мына теңсіздікті қанағаттандырады
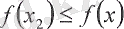
Жоғарыда көрсетілген
 функциясының мәнін
функциясының мәнін
 функциясының
функциясының
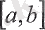 кесіндісіндегі
ең үлкен
мәні, ал
кесіндісіндегі
ең үлкен
мәні, ал
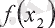 функциясының мәнін
функциясының мәнін
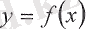 функциясының
функциясының
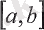 кесіндісіндегі
ең кіші
мәні деп атаймыз.
кесіндісіндегі
ең кіші
мәні деп атаймыз.
Айтылған теореманы қысқаша төмендегідей түрде баяндауға болады:
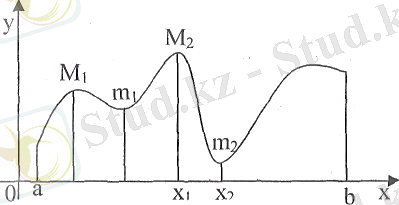
Берілген
 кесіндісінде үзіліссіз болатын функция осы кесіндіде ең кемінде бір рет ең үкен
М
мәнін және ең кіші
т
мәнін қабылдайды. (7-сурет)
кесіндісінде үзіліссіз болатын функция осы кесіндіде ең кемінде бір рет ең үкен
М
мәнін және ең кіші
т
мәнін қабылдайды. (7-сурет)
Сурет
Сурет
1-теорема.
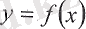 функциясы
функциясы
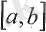 кесіндісінде үзіліссіз және осы кесіндінің шеткі нүктелерінде әр түрлі таңбадағы мәндер қабылдаса, онда
а
және
b
нүктелерінің арасынан ең кемінде бір х = с нүктесі табылып, осы нүктеде функциянелге айналады (8-сурет) :
кесіндісінде үзіліссіз және осы кесіндінің шеткі нүктелерінде әр түрлі таңбадағы мәндер қабылдаса, онда
а
және
b
нүктелерінің арасынан ең кемінде бір х = с нүктесі табылып, осы нүктеде функциянелге айналады (8-сурет) :
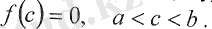
8-теорема.
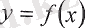 функциясы
функциясы
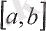 кесіндісінде анықталған және үзіліссіз болсын. Егер осы кесіндінің шеткі нүктелерінде функция тең емес мәндер қабылдаса, яғни
кесіндісінде анықталған және үзіліссіз болсын. Егер осы кесіндінің шеткі нүктелерінде функция тең емес мәндер қабылдаса, яғни
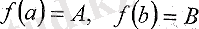 болса, онда
A
және
В
сандарының арасындағы қандайда болмасын
µ
санына,
болса, онда
A
және
В
сандарының арасындағы қандайда болмасын
µ
санына,
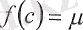 болатын
а
және
b
нүктелерінің арасында жататын
х = с
нүктесі табылады.
болатын
а
және
b
нүктелерінің арасында жататын
х = с
нүктесі табылады.
Келесі мысалдарды қарастырамыз:
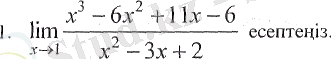
Шешуі: Бұл есепте
 ұмтылғанда
ұмтылғанда
 анықталмағандығын аламыз, яғни
анықталмағандығын аламыз, яғни
 ұмтылғанда
ұмтылғанда
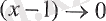 ұмтылады, сондықтан бөлшектің алымынан және бөлімінен
ұмтылады, сондықтан бөлшектің алымынан және бөлімінен
 ернегінен құтылу керек ол үшін, бөлшектің алымын және бөлімін жіктейміз:
ернегінен құтылу керек ол үшін, бөлшектің алымын және бөлімін жіктейміз:

Шешуі: Бұл есепте
 ұмтылғанда
ұмтылғанда
 анықталмағандығын аламыз. Мұндай анықталмағандықты ашу үшін, бөлшектің алымынан және бөлімінен
х -
тің ең үлкен дәрежесін жақшаның сыртына шығарып қысқартамыз:
анықталмағандығын аламыз. Мұндай анықталмағандықты ашу үшін, бөлшектің алымынан және бөлімінен
х -
тің ең үлкен дәрежесін жақшаның сыртына шығарып қысқартамыз:
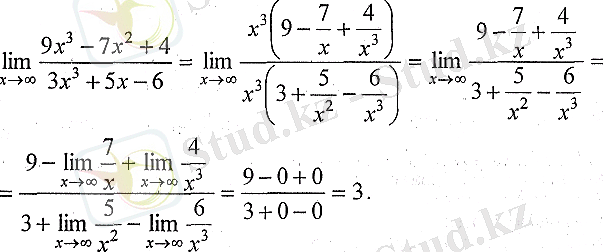
3.
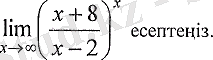
Шешуі: Бүл есепте
 ұмтылғанда
ұмтылғанда
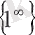 анықталмағандығын аламыз, сондықтан оны екінші тамаша шек
анықталмағандығын аламыз, сондықтан оны екінші тамаша шек
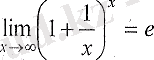 формуласын қолданып шығарамыз:
формуласын қолданып шығарамыз:

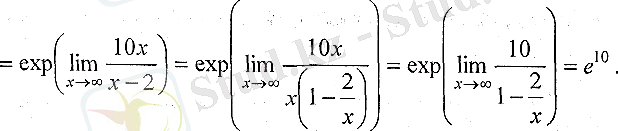
4.
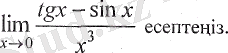
Шешуі: Бұл есепте
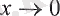 ұмтылғанда бөлшектің алымындағы тригонометрияльтқ функциялардың айырмасының
ұмтылғанда бөлшектің алымындағы тригонометрияльтқ функциялардың айырмасының
 қатынасынан
қатынасынан
 анықталмағандығын аламыз, яғни бірінші тамаша шек
анықталмағандығын аламыз, яғни бірінші тамаша шек
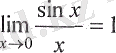 қолданып шығарамыз:
қолданып шығарамыз:

2 Үзіліссіз функциялардың локальды қасиеттері. Элементар функциялардың үзіліссіздігі
2. 1 Үзіліссіз функциялардың кейбір локальды қасиеттері
Дәлелденген теоремалардың шарттарында функцияның аргументі нақты санға ұмтылғанда нақты мәнді шегі бар болуы талап етілген еді. Үзіліссіз функциялар, әрине, ол шарттарды қанағаттандырады (алдыңғы пункттегі 1 0 -ді қараңыз), сондықтан аталған теоремалардан салдар ретінде үзіліссіз функциялардың келесі маңызды қасиеттері шығады (ол теоремаларды қолданғанда а -ның орнына х о -ді қою керек) .
1-теорема. Әрбір функцияның үзіліссіздік нүктесі локальді шенелу нүктесі де болады.
2 - т е о р е м а. Егер
f
функциясы
х
0
нүктесінде үзіліссіз болып, сол нуктеде қабылданған
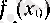 мәні оң (теріс) болса, онда
х
0
-дің белгілі бір маңайында
f
фумкциясының барлық мәндері де оң (теріс) болады.
мәні оң (теріс) болса, онда
х
0
-дің белгілі бір маңайында
f
фумкциясының барлық мәндері де оң (теріс) болады.
Дәлірек айтқанда, әрбір
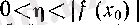 теңсіздіктерін қанағаттандыратып
η
оң саны бойынша барлық
теңсіздіктерін қанағаттандыратып
η
оң саны бойынша барлық
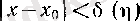 үшін
f (х
0
)
оң болғанда
үшін
f (х
0
)
оң болғанда
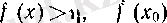 теріс болғанда
теріс болғанда
 теңсіздіктері орындалатын
теңсіздіктері орындалатын
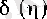 оң саны табылады. Қысқаша: функция үзіліссіздік нүктесінің қасында таңбасын сақтайды.
оң саны табылады. Қысқаша: функция үзіліссіздік нүктесінің қасында таңбасын сақтайды.
Расында да, теоремада
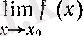 саны орнына функцияның үзіліссіздігі бойынша
саны орнына функцияның үзіліссіздігі бойынша
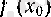 санын қоюға болады.
санын қоюға болады.
С а л д а р. Егер f функциясы х 0 нүктесінде үзіліссіз болып, оның белгілі бір ойылған маңайындағы барлық нүктелерде қабылданатын мәні нольге тең болса не х 0 -діц кез келген ойылған маңайында оң және теріс таңбалы мәндерді қатар қабылдаса, онда f (x o ) =0 болады.
Расында да,
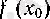 оң (теріс) болса, онда
х
0
-
дің белгілі бір'маңайында
f
функциясының мәндерінің бәрі де тек қана оң (теріс) таңбалы болар еді.
оң (теріс) болса, онда
х
0
-
дің белгілі бір'маңайында
f
функциясының мәндерінің бәрі де тек қана оң (теріс) таңбалы болар еді.
3-теорсма. Егер
f
және
g
функциялары
х
а
нүктесінде үзіліссіз болса, онда
f + g, f - g, f*g
жәие
f/g
функциялары да сол нүктеде үзіліссіз болады (әрине, соңғы жағдайда
g (х
0
) ≠
0 шарты орындалуы тиіс), ал х
о
-дің белгілі бір ойылған маңайында
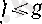 болса, онда
болса, онда
 теңсіздігі орындалады.
теңсіздігі орындалады.
Басқа сөзбен айтқанда, үзіліссіздік ұғымы арифметикалық амалдар бойынша тұйық болады.
Дәлелдеуі. f және g үзіліссіз болғандықтан, теореманың шарттарында b = f (x 0 ), c = g (x 0 ) болады, демек, сол теореманың қорытындысындағы
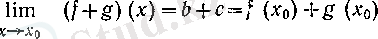
теңдігі f+g функциясының х 0 нүктесіндегі үзіліссіздігін бейнелейді. Басқа жағдайлар да, дәл осылай, қарастырылады.
4-теорема. Егер
X
жиынында анықталған
f
функциясы
 нүктесінде үзіліссіз болса, У жиынында анықталған
g
функциясы
нүктесінде үзіліссіз болса, У жиынында анықталған
g
функциясы
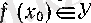 нүктесінде үзіліссіз болса, онда
нүктесінде үзіліссіз болса, онда
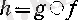 күрделі функциясы
х
0
нүктесінде үзіліссіз болады.
күрделі функциясы
х
0
нүктесінде үзіліссіз болады.
Басқа сөзбен айтқанда, үзіліссіз функциялардан құрылған күрделі функция үзіліссіз болады.
Расында да, f-тің үзіліссіздігі бойынша теореманың шартында
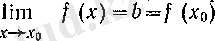 болады, демек, сол теореманың қорытындысындағы
болады, демек, сол теореманың қорытындысындағы
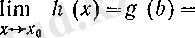
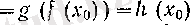 теңдігі
h(x) =g(f(x) )
күрделі фупкдиясының х
0
нүктесінде үзіліссіз екенін бейнелейді.
теңдігі
h(x) =g(f(x) )
күрделі фупкдиясының х
0
нүктесінде үзіліссіз екенін бейнелейді.
С а л д а р. Егер х 0 нүктесінде f үзіліссіз болса, онда сол пуктеде f функциясы да үзіліссіз болады.
Расында да,
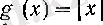 функциясының үзіліссіздігі айқын.
функциясының үзіліссіздігі айқын.
2. 2 Элементар функциялардың үзіліссіздігі
Алдыңғы тарауда кейбір элементар функциялар үшін шығарылған шек табу есептерін үзіліссіздік ұғымын пайдалапып басқаша айтуға болады.
1°. Әрбір көпмүшелік барлық нақты сандар жиынында үзіліссіз.
2°. Әрбір рациоиал функция өзінің анықталу жиынында үзіліссіз, яғни қайсыбір а 0 , а 1 . . . , а п , b о , b 1 . . . , b т нақты сандары үшін
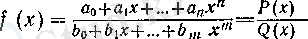
болса, онда
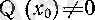 теңсіздігін қанағаттандыратын кез келген
Хо
нақты саны үшін
теңсіздігін қанағаттандыратын кез келген
Хо
нақты саны үшін
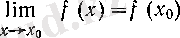 болады,
болады,
Бұл 3 (III тарау, § 3) -пунктте дәлелденген еді.
3°. Логарифмдік функция оң нақты сандар жиынында үзіліссіз, яғни әрбір а≠ 1 және х о оң нақты сандары үшін
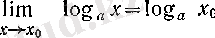
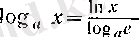 Бұл
а = е
үшін 1 (III тарау, § 2) -пунктте дәлелденген еді, ал жалпы жағдайда тепе-теңдігінен шығады.,
Бұл
а = е
үшін 1 (III тарау, § 2) -пунктте дәлелденген еді, ал жалпы жағдайда тепе-теңдігінен шығады.,
4°. Көрсеткіштік функция барлық нақты сандар жиынында үзіліссіз, яғни әрбір
а>0
және
х
0
нақты сандары үшін, .
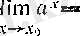 = а
х
.
= а
х
.
Бұл 1 (III тарау, § 2) -пунктте дәлелденген еді.
5°. Дәрежелік фупкция өзінің анықталу жиыныпда үзіліссіз.
Дәл айтқанда,
f
(х) =х
а
функциясы
а
оң нақты can болғанда
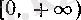 жиынында,
а
теріс нақты caн болғанда
жиынында,
а
теріс нақты caн болғанда
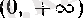 жиынында,
жиынында,
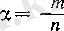 (т
- бүтін,
п
- тақ сандар) оң сан болғанда
(т
- бүтін,
п
- тақ сандар) оң сан болғанда
 жиынында,
жиынында,
 теріс caн болғанда
теріс caн болғанда

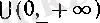 жиынында үзіліссіз болады.
жиынында үзіліссіз болады.
Дәлелдеуі.
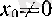 болғанда барлық
а
сандары үшін
болғанда барлық
а
сандары үшін
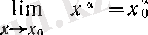 теңдігі 4 (III тарау, § 4) -пунктте дәлелденген еді.
теңдігі 4 (III тарау, § 4) -пунктте дәлелденген еді.
Сондықтан, 5°-ді толық дәлелдеу үшін а оң нақты caн болғанда
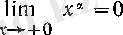 (2)
(2)
теңдігін дәлелдеу қалды.
ɛ
оң саны берілсін. Онда
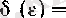
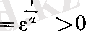 саны үшін
саны үшін
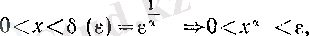 яғни (2) дәлелденді.
яғни (2) дәлелденді.
6°. sin х және cos х функциялары барлық нақты сандар жиынында үзіліссіз, яғни әрбір х 0 нақты саны үшін,
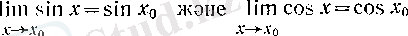 (3)
(3)
Дәлелдеуі. ɛ>0 және
х
0
нақты сандары берілсін. Онда
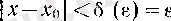 ; теңсіздігін қанағаттандыратып барлық
х
сандары үшін
; теңсіздігін қанағаттандыратып барлық
х
сандары үшін
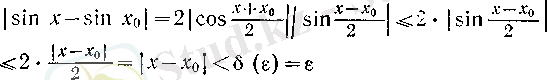
болады, яғни sin
x
функциясының үзіліссіздігі дәлелденді. Бұнда
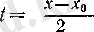 үшін 3 (III тарау, § 3) -пунктте дәлелденген
үшін 3 (III тарау, § 3) -пунктте дәлелденген
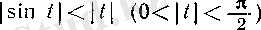 теңсіздігі пайдаланылды. cos
х
функциясының үзіліссіздігі келесі
теңсіздігі пайдаланылды. cos
х
функциясының үзіліссіздігі келесі
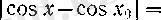
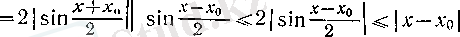
теңсіздігінен айқын түрде шығады.
7°.
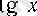 және
және
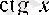 функциялары өздерінің анықталу жиынында үзіліссіз, яғни барлық
функциялары өздерінің анықталу жиынында үзіліссіз, яғни барлық
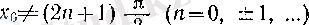
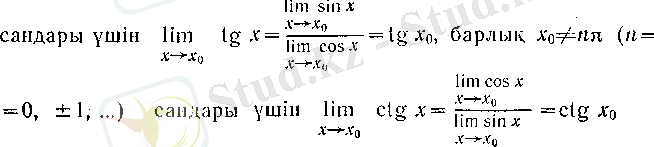
болады.
Бұл 6° мен 3-теоремадан шығады.
8°. Кері тригонометриялық функциялар өздерінің анықталу жиындарында үзіліссіз.
Бұл 3 (§ 2) -пунктте дәлелденеді.
1°-8° тұжырымдарын жалпылап, былай айтуға болады:
Негізгі элементар функциялар өздерінің анықталу жиындарында үзіліссіз болады.
Бұдан, элементар функцияның анықтамасы мен күрделі функцияның үзіліссіздігі туралы теорема бойынша келесі жалпы қорытынды шығады: Элементар функциялар әздерінің анықталу жиындарында үзіліссіз болады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz