Функцияның жоғарғы және төменгі шектері: шектер теориясы және нақты функцияның құрылысы


Курстық жұмыс
Тақырыбы: Функцияның жоғарғы және төменгі шектері
Мазмұны
Кіріспе . . .
1 Функцияның шектері теориясы . . .
2 Функцияның жоғарғы және төмен шектері . . .
2. 1 Функцияның дербес шегі . . .
2. 2 Функцияның жоғарғы және төменгі шектері . . .
2. 3 Нақты функцияның құрылысы туралы . . .
2. 4 Жалпы жағдай . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
Қосымша . . .
3
4
11
11
12
16
20
21
23
24
Кіріспе
Әуелі дербес шектің екі анықтамасын берейік.
 функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын.
a
- нақты сан,
функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын.
a
- нақты сан,
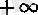 немесе
немесе
 -тің бірі болсын, яғни
-тің бірі болсын, яғни
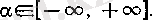
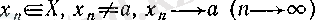 шарттарын қанағаттандыратын белгілі бір
шарттарын қанағаттандыратын белгілі бір
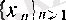 тізбегі мен оған сәйкес
тізбегі мен оған сәйкес
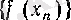 тізбегі үшін
тізбегі үшін
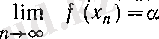 теңдігі орындалса, онда
а
-ны
теңдігі орындалса, онда
а
-ны
 функциясының
а
нүктесіндегі
дербес шегі
деп атайды.
функциясының
а
нүктесіндегі
дербес шегі
деп атайды.
Курстық жұмыстың мақсаты: функцияның жоғарғы және төменгі шектерін зерттеу.
Міндеттері:
- функцияның шектері теориясын қарастыру;
- функцияның жоғарғы және төмен шектерін зерттеу;
- функцияның дербес шегін қарастыру;
- функцияның жоғарғы және төменгі шектері және нақты функцияның құрылысы туралы ашу, жалпы жағдай қарастыру.
Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімнен, қорытындыдын, әдебиеттер тізімінен, қосымшадан құрылады.
1 Функцияның шектері теориясы
Анықтама.
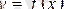 функциясы
функциясы
 нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін d оң саны табылып, x -тің
нүктесінің бір төңірегіндегі нүктелерде анықталсын делік. Егер әрбір e>0 үшін d оң саны табылып, x -тің
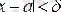 теңсіздігін қанағаттандыратын барлық мәндері үшін, мына
теңсіздігін қанағаттандыратын барлық мәндері үшін, мына
 теңсіздік орындалса,
теңсіздік орындалса,
 шамасы
шамасы
 -тің
-тің
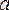 -ға ұмтылғандағы
-ға ұмтылғандағы
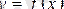 функциясының (
функциясының (
 нүктесіндегі ) шегі деп аталады.
нүктесіндегі ) шегі деп аталады.
Осы анықтамадағы
 шамасының функцияның анықталу облысына кіруі шарт емес, бірақ
шамасының функцияның анықталу облысына кіруі шарт емес, бірақ
 -ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруі шарт.
-ға мейлінше жақын нүктелердіңфункцияның анықталу облысына кіруі шарт.
Егер
 шамасы
шамасы
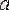 -ға ұмтылғанда,
-ға ұмтылғанда,
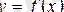 функциясының мәні
функциясының мәні
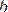 -ға ұмтылса, оны былайша жазатын боламыз
-ға ұмтылса, оны былайша жазатын боламыз
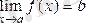 .
.
Анықтамадағы
 және
және
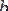 шамалары сан болуы да, не ±¥ болуы да мүмкін.
шамалары сан болуы да, не ±¥ болуы да мүмкін.
Егер
 -ның шамасы
-ның шамасы
 символдарының бірі болса,
символдарының бірі болса,
 - шексіз үлкен деп аталады, мұны былай жазамыз
- шексіз үлкен деп аталады, мұны былай жазамыз
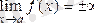 .
.
Егер әрбір e>0 үшін
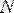 саны табылып,
саны табылып,
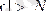 үлкен болғанда
үлкен болғанда
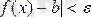 теңсіздігі орындалса,
теңсіздігі орындалса,
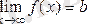 деп жазамыз.
деп жазамыз.
Егер
 -ның шамасы
-ның шамасы
 символдарының бірі болса,
символдарының бірі болса,
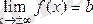 деп жазамыз.
деп жазамыз.
Енді функцияның шегінің геометриялық мағынасын анықтайық. Айталық
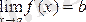 делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
делік. Бұлай деу, берілген e>0 үшін d>0 саны табылып,
 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық
 үшін
үшін
 теңсіздігі орындалады деген сөз.
теңсіздігі орындалады деген сөз.
Басқаша айтқанда: аргумент
x
-тің
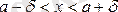 теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
теңсіздіктерін қанағаттандыратын барлық мәндеріне сәйкес келетін ¦(x) функциясының барлық мәндері
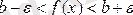 теңсіздігін қанағаттандыруы тиіс.
b
-саны
теңсіздігін қанағаттандыруы тиіс.
b
-саны
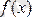 функциясының
х
шамасы
функциясының
х
шамасы
 -ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.
-ға ұмтылғандағы шегі дегенді геометрияда былай түсіндіруге болады.
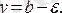
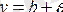 түзулер шектеген алап қандай болса да,
түзулер шектеген алап қандай болса да,
 нүктесінің төңірегіне
нүктесінің төңірегіне
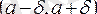 маңайын салуға болады (яғни d>0 саны табылады) . Олай болса, абсциссалары
маңайын салуға болады (яғни d>0 саны табылады) . Олай болса, абсциссалары
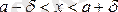 теңсіздіктерін қанағаттандыратын
теңсіздіктерін қанағаттандыратын
 қисығының барлықнүктелері
қисығының барлықнүктелері
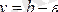 ,
,
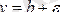 түзулері шектеген алаптың ішінде жатады (тек абсциссасы
түзулері шектеген алаптың ішінде жатады (тек абсциссасы
 -ға тең нүкте ғана алапқа енбей қалуы мүмкін) . Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
-ға тең нүкте ғана алапқа енбей қалуы мүмкін) . Функция шегінің анықтамасындағы d>0 саны e санына тәуелді, жалпы айтқанда e өзгерсе d да өзгереді . Бірнеше мысалдар қарастырайық.
1)
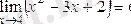 болатынын көрсету керек.
болатынын көрсету керек.
Алдын ала e>0 саны берілсін. Оған сәйкес
 -тің
-тің
 (*)
(*)
теңсіздігін қанағаттандыратын барлық мәндері үшін
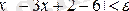 (**)
(**)
теңсіздігі, яғни
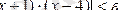 теңсіздігі орындалатын d>0 санын табайық. Ал (*) -дан
теңсіздігі орындалатын d>0 санын табайық. Ал (*) -дан
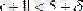 теңсіздігі шығады. Демек,
теңсіздігі шығады. Демек,
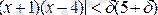 . (***)
. (***)
(**) мен (***) -дан мына қорытындыға келеміз: егер d санын d(5+d) =e тендігін қанағаттандыратын етіп алсақ, (*) (***) да орындалады.
Сонымен,
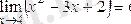 екендігі дәлелденеді.
екендігі дәлелденеді.
2)
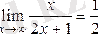 екендігін дәлелдеу керек.
екендігін дәлелдеу керек.
Алдын ала e>0 cаны берілген делік. Сонда аргумент
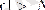 теңсіздігін қанағаттандырысымен
теңсіздігін қанағаттандырысымен
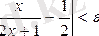 N
санын іздеуіміз керек.
N
санын іздеуіміз керек.
Ал,
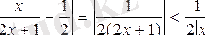 . Cондықтан
. Cондықтан
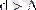 болғанда
болғанда
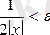 теңсіздігі орындалады. Бұдан
теңсіздігі орындалады. Бұдан
 . Демек, егер
. Демек, егер
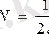 деп алсақ,
деп алсақ,
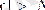 болғанда
болғанда
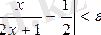 , яғни
, яғни
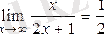 болатыны айқын.
болатыны айқын.
Ескерту. Егер
 функциясы
функциясы
 шамасына ұмтылғанда,
x
-тің
шамасына ұмтылғанда,
x
-тің
 -ға ұмтылуы тек
-ға ұмтылуы тек
 -дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
-дан кіші мәндер қабылдау арқылы ғана болса, былай жазып
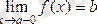 ,
,
 ді функцияның
ді функцияның
 нүктесіндегі сол жақты шегі дейді.
нүктесіндегі сол жақты шегі дейді.
Егер
х
тек
 -дан үлкен мәндер қабылдайтын болса, былай жазып
-дан үлкен мәндер қабылдайтын болса, былай жазып
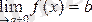 ,
,
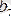 -ні функцияның
-ні функцияның
 нүктесіндегі оң жақты шегі дейді.
нүктесіндегі оң жақты шегі дейді.
Ескерту. Егер аргумент
х
-тің берілген анықталу облысындағы барлық мәндері үшін
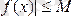 М саны табылса,
М саны табылса,
 функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
функциясы қарастырылып отырған облыста шектелген деп аталады. Егер ондай М саны табылмаса функция
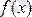 берілген облыста шектелмеген делінеді.
берілген облыста шектелмеген делінеді.
Шексіз аз шама және оның қасиеттері.
Анықтама. Егер
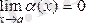 не
не
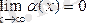 болса,
болса,
 функциясы
функциясы
 не
x
®¥ болғанда шексіз аз шама делінеді.
не
x
®¥ болғанда шексіз аз шама делінеді.
Шектің анықтамасына сүйеніп, жоғарыдағы анықтаманы былайша тұжырымдауға болады: алдынала берілген кез-келген жеткілікті аз e>0 саны үшін
 теңсіздігі орындалатын
x -
тың мәндері үшін
теңсіздігі орындалатын
x -
тың мәндері үшін
 теңсіздігі орындалатындай d саны табылса, a(x) шексіз аз шама делінеді (x®
теңсіздігі орындалатындай d саны табылса, a(x) шексіз аз шама делінеді (x®
 ) .
) .
Мысалы.
1) функция a(x) =(x-2)
2
, x шамасы 2-ге ұмтылғанда шексіз аз шама, өйткені
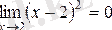 .
.
2) функция a(x) =
 , х®¥ болғанда шексіз аз шама, өйткені
, х®¥ болғанда шексіз аз шама, өйткені
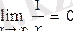 .
.
Теорема. Егер
 функциясы
b
санымен шексіз аз шама a-нің қосындысына тең болса, яғни y=b+a болса, lіm y=b (x®a не х®¥) болады. Керісінше, егер
функциясы
b
санымен шексіз аз шама a-нің қосындысына тең болса, яғни y=b+a болса, lіm y=b (x®a не х®¥) болады. Керісінше, егер
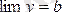 болса,
болса,
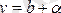 деп жазуға болады. Мұндағы a шексіз аз шама.
деп жазуға болады. Мұндағы a шексіз аз шама.
Теорема. Егер
 шамасы
шамасы
 -ға ұмтылғанда a(x) нольге ұмтылса, y=
-ға ұмтылғанда a(x) нольге ұмтылса, y=
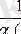 шексіз үлкен шамаға ұмтылады.
шексіз үлкен шамаға ұмтылады.
Теорема. Бірнеше (саны шектеулі) шексіз аз шамалардың алгебралық қосындысы шексіз аз шама болады.
Теорема. Шексіз аз шама a(x) -тың шектелген g(x) функциясына көбейтіндісі (x®
 , x®¥) шексіз аз шама.
, x®¥) шексіз аз шама.
Салдар. Егер lіm a(x) =0, lіm b(x) =0 болса, lіmab=0.
Салдар. Егер lіm a(x) =0, c=const болса, lіm ca=0.
Теорема. Егер lіma(x) =0, lіmb(x) ¹0 болса a(x) ·b -1 (x) -шексіз аз шама болады.
Шектер туралы негізгі теоремалар.
Теорема. Бірнеше (саны шектеулі) функциялардың қосындысының шегі сол функциялардың шектерінің қосындысына тең
lіm(u 1 +u 2 + . . . +u k ) = lіm u 1 +lіm u 2 + . . . +lіm u k .
Теорема. Бірнеше (саны шектеулі) айнымалы шегі сол шамалардың тең:
lіm(u 1 u 2 . . . u k ) =lіm u 1 lіm u 2 . . . lіm u k .
Теорема.
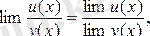
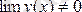 .
.
Теорема. Егер u(x),
 және v(x) функцияларының сәйкес мәндері мына
және v(x) функцияларының сәйкес мәндері мына
 теңсіздіктерін қанағаттандырса және u(x) пен v(x) функциялары
теңсіздіктерін қанағаттандырса және u(x) пен v(x) функциялары
 не
не
 -да бір
b
санына ұмтылса, онда
-да бір
b
санына ұмтылса, онда
 -те сол шекке ұмтылады.
-те сол шекке ұмтылады.
Теорема. Егер
 шамасы
шамасы
 -ға (не ¥-ке) ұмтылғанда теріс емес
-ға (не ¥-ке) ұмтылғанда теріс емес
 функциясы
функциясы
 шегіне ұмтылса, онда
шегіне ұмтылса, онда
 -нольден кіші болмайды.
-нольден кіші болмайды.
Теорема. Егер үдемелі айнымалы шама
 шектелген шама, яғни
шектелген шама, яғни
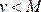 болса, онда бұл айнымалы шаманың шегі бар, яғни
болса, онда бұл айнымалы шаманың шегі бар, яғни
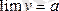 болады және ол
болады және ол
 .
.
Кемімелі айнымалы шама үшін де осыған ұқсас теорема орындалады.
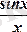 функциясының
функциясының
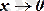 шегі
шегі
 функциясы
функциясы
 да
да
 түріндегі анықталмағандықты береді.
түріндегі анықталмағандықты береді.
Теорема.
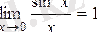 . (*)
. (*)
(*) формуласын 1-ші тамаша шек деп атайды.
Есеп шығарғанда, бізге қажет болатын маңызы зор бірнеше шектерді (бірінші тамаша шектің көмегімен дәлелденетін) келтірейік:
1)
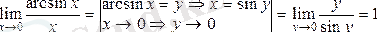 .
.
2)
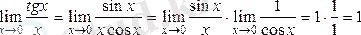 .
.
3)
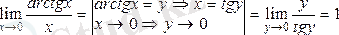 .
.
Айнымалы шаманың шегі. Тізбектің шегі.
Анықтама. Егер бізге қалағанымызша аз e оң саны берілсе және айнымалы шама
 -тің бір мәнікөрсетіліп, одан кейінгі мәндерінің бәрі мына теңсіздікті
-тің бір мәнікөрсетіліп, одан кейінгі мәндерінің бәрі мына теңсіздікті
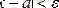 қанағаттандырса, түрақты
қанағаттандырса, түрақты
 саны айнымалы
саны айнымалы
 -тің шегі делінеді де, былайша жазылады:
-тің шегі делінеді де, былайша жазылады:
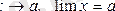
Сандар тізбегі

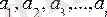 үшін бұл анықтаманы былайша айтуға болар еді.
үшін бұл анықтаманы былайша айтуға болар еді.
Егер де алдын ала кез келген аз eоң саны берілсе,
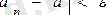 теңсіздігі
теңсіздігі
 нөмірден бастап орындалатын болса, онда түрақты сан
нөмірден бастап орындалатын болса, онда түрақты сан
 -ны тізбектің шегі дейді де
-ны тізбектің шегі дейді де
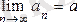 cимволымен жазады. Мұндағы lіm латын тіліндегі lіmes (шек) деген сөзден қысқартылып алынған. Бұл жағдайды былайша:
cимволымен жазады. Мұндағы lіm латын тіліндегі lіmes (шек) деген сөзден қысқартылып алынған. Бұл жағдайды былайша:
 тізбегі түрақты
тізбегі түрақты
 санына ұмтылады деп те айтады және былай жазады:
санына ұмтылады деп те айтады және былай жазады:

 ; тізбекті
; тізбекті
 санына жинақталады деп те атайды.
санына жинақталады деп те атайды.
Мысалы. 1) жалпы мүшесі
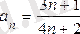 түрінде берілген сан тізбегі өзінің шегі
түрінде берілген сан тізбегі өзінің шегі
 -ке ұмтылады.
-ке ұмтылады.
Шынында, алдын ала
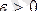 санын алып,
санын алып,
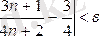 теңсіздігі
теңсіздігі
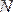 номерінің қай мәнінен бастап орындалатынын анықталық. Бұл теңсіздікті мына түрге түрлендіреміз
номерінің қай мәнінен бастап орындалатынын анықталық. Бұл теңсіздікті мына түрге түрлендіреміз
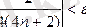 бұдан
бұдан
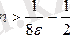 .
.
Демек,
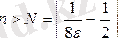 болғанда, анықтамаға сәйкес
болғанда, анықтамаға сәйкес
 қарастырылып отырған тізбектің шегі болады.
қарастырылып отырған тізбектің шегі болады.
2) Тізбектің жалпы мүшесі былай
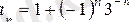 берілсе, бұл тізбектің шегі бірге тең.
берілсе, бұл тізбектің шегі бірге тең.
Шынында,
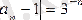 кез-келген e>0үшін
кез-келген e>0үшін
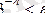 теңсіздігі
теңсіздігі
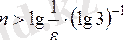 болғанда орындалады.
болғанда орындалады.
Бұдан кез келген тізбектің шегі болады деген ұғым тумауы керек.
Мысалы. Тізбектің мүшелері мына формулалармен берілсе
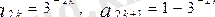
мұнда k-ның үлкен номерлерінен бастап, жұп номерлі мүшелерінің нольден айырмашылығы керегінше аз болады да, тақ номерлері мүшелерінің бірден айырмашылығы аз болады. Сондықтан тізбектің шегі болмайды.
Анықтама. Егер алдынала берілген әрбір оң сан М үшін айнымалы
 -тің бір мәнікөрсетіліп және кейінгі мәндерінің бәрі мына теңсіздікті
-тің бір мәнікөрсетіліп және кейінгі мәндерінің бәрі мына теңсіздікті
 қанағаттандырса,
қанағаттандырса,
 шексіздікке ұмтылады дейміз. Бұндай айнымалы шаманы шексіз үлкен айнымалы шама деп,
шексіздікке ұмтылады дейміз. Бұндай айнымалы шаманы шексіз үлкен айнымалы шама деп,
 cимволымен белгілейді.
cимволымен белгілейді.
Мысалы.
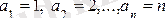 тізбегі шексіздікке ұмтылады.
тізбегі шексіздікке ұмтылады.
e саны.
 функциясының
функциясының
 шегі
шегі
Жалпы мүшесі
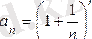 түрінде берілген сан тізбегінің шегін
e
саны деп атайды, яғни
түрінде берілген сан тізбегінің шегін
e
саны деп атайды, яғни
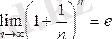 .
e-саны иррационал сан және оның жуық мәні мынадай e=2. 71828128 . . .
.
e-саны иррационал сан және оның жуық мәні мынадай e=2. 71828128 . . .
Теорема.
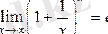 . (**)
. (**)
(**) -формуласын 2-ші тамаша шек деп атайды.
Егерде (**) формулада
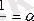 десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
десек, онда х®¥ Þ a®0 (a¹0) болады да, ол формуланы былай жазуға болады:
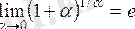 .
.
e-cанын пайдаланып шығарылатын кейбір шектерді келтірейік:
1)
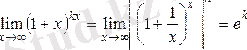 .
.
2)
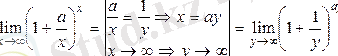 e
e
 .
.
3)
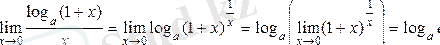 .
.
3')
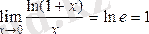 .
.
4)
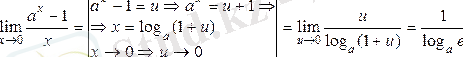
5)
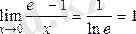
6)
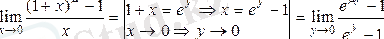
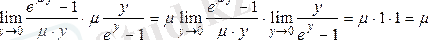
Егерде
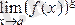 шегін
шегін
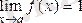 және
және
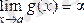 болған жағдайда есептеп шығару керек болса, онда
болған жағдайда есептеп шығару керек болса, онда
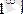 түріндегі анықталмағандық алар едік.
түріндегі анықталмағандық алар едік.
Бұл секілді анықталмағандықтарды ашу үшін, берілген функцияның
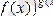 негізі мен дәреже көрсеткішін мына формуланы
негізі мен дәреже көрсеткішін мына формуланы
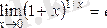 қолдану мүмкін болатындай етіп түрлендіру керек .
қолдану мүмкін болатындай етіп түрлендіру керек .
Мысалы.
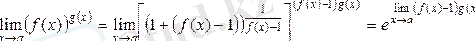 .
.
Осыдан,
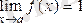 ,
,
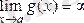 жағдайда, мына формула табылады
жағдайда, мына формула табылады
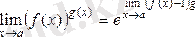 (бұл жерде үзіліссіз функциялардың композициясының үзіліссіздігі пайдаланылды) .
(бұл жерде үзіліссіз функциялардың композициясының үзіліссіздігі пайдаланылды) .
Мысал келтірейік,
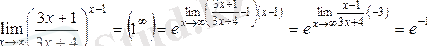 .
.
Ескерту. Егер логарифмдердің негізін e деп алсақ, мұндай логарифмдер натуралдық логарифмдер, не неперлік логарифмдер делінеді. Непер (1550-1617) - логарифм кестелерін алғашқы жасаушылардың бірі.
Егер х=e y болса, y-ті х санының натуралдық логарифмі дейді, y=lnx деп жазады (y=log e x деудің орнына) .
Бір санның ондық логарифмі мен натуралдық логарифмдерінің байланысын былай табады.
Егер y=lgx, не х=10
y
болса, оны
е
негізінде логарифмдесек ln
x=y×
ln10
,
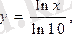
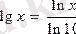 .
.
Егер
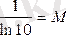 десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
десек, lgx=М×lnx болады. М-ауысу модулі деп аталады.
Осылайша, егер санның натуралдық логарифмі белгілі болса, онда оның ондық логарифмін ауысу модуліне көбейту арқылы табады.
2 Функцияның жоғарғы және төмен шектері
2. 1 Функцияның дербес шегі
Әуелі дербес шектің екі анықтамасын берейік.
 функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын.
a
- нақты сан,
функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын.
a
- нақты сан,
 немесе
немесе
 -тің бірі болсын, яғни
-тің бірі болсын, яғни
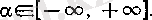
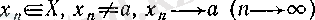 (1)
(1)
шарттарын қанағаттандыратын белгілі бір
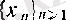 тізбегі мен оған сәйкес
тізбегі мен оған сәйкес
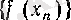 тізбегі үшін
тізбегі үшін
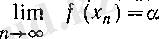 (2)
(2)
теңдігі орындалса, онда
а
-ны
 функциясының
а
нүктесіндегі
дербес шегі
деп атайды.
функциясының
а
нүктесіндегі
дербес шегі
деп атайды.
Дербес шектің
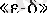 тіліндегі анықтамасы. Егер әрбір
тіліндегі анықтамасы. Егер әрбір
 және
және
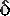 оң сандары үшін
оң сандары үшін
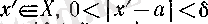 (3)
(3)
және
а
нақты сан болғанда
 болғанда
болғанда
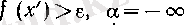 болғанда
болғанда
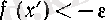 шарттарын қанағаттандыратын
х'
саны табылса, онда
а
саны
f
функциясының
а
нүктесіндегі дербес шегі деп аталады.
шарттарын қанағаттандыратын
х'
саны табылса, онда
а
саны
f
функциясының
а
нүктесіндегі дербес шегі деп аталады.
Бұл анықтамалар эквивалентті болады. Алдымен
а
нақты саны дербес шектің тізбектер тіліндегі анықтамасы бойынша
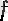 функциясының
а
нүктесіндегі дербес шегі болып, ɛ және δ оң сандары берілсін. Берілген ɛ оң саны үшін (2) бойынша
функциясының
а
нүктесіндегі дербес шегі болып, ɛ және δ оң сандары берілсін. Берілген ɛ оң саны үшін (2) бойынша
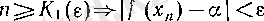
шарты орындалатын
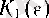 оң бүтін саны табылады. Берілген δ оң саны үшін (1) бойынша
оң бүтін саны табылады. Берілген δ оң саны үшін (1) бойынша
 (4)
(4)
шарты орындалатын
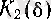 оң бүтін саны табылады. Бұдан
оң бүтін саны табылады. Бұдан
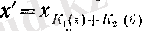 саны үшін (3) және (4) шарттары орындалуы айқын, демек, дербес шектің
саны үшін (3) және (4) шарттары орындалуы айқын, демек, дербес шектің
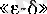 тіліндегі анықтамасы бойынша
а
нақты саны
тіліндегі анықтамасы бойынша
а
нақты саны
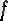 функциясының
а
нүктесіндегі дербес шегі болады.
функциясының
а
нүктесіндегі дербес шегі болады.
Кері, дербес шектің
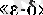 тіліндегі анықтамасы бойынша
а
нақты саны
тіліндегі анықтамасы бойынша
а
нақты саны
 функциясының
а
нүктесіндегі дербес шегі болсын.
функциясының
а
нүктесіндегі дербес шегі болсын.
Әрбір
п
оң бүтін нақты саны үшін
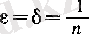 болғанда (3) және (4) шарттарын қанағаттандыратын
х'
санын
х
п
символымен белгілесек, онда
болғанда (3) және (4) шарттарын қанағаттандыратын
х'
санын
х
п
символымен белгілесек, онда
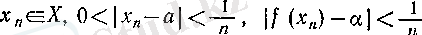
болады. Бұдан
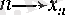 тізбегі үшін (1) және (2) шарттары орындалуы айқын, яғни дербес шектің тізбектер тіліндегі анықтамасы бойынша
а
нақты саны
тізбегі үшін (1) және (2) шарттары орындалуы айқын, яғни дербес шектің тізбектер тіліндегі анықтамасы бойынша
а
нақты саны
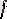 функциясының
а
нүктесіндегі дербес шегі болады.
функциясының
а
нүктесіндегі дербес шегі болады.
 Сонымен, дербес шек нақты сан болғанда екі анықтаманың эквиваленттілігі дәлелденді.
Сонымен, дербес шек нақты сан болғанда екі анықтаманың эквиваленттілігі дәлелденді.
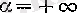 және жағдайлары да дәл осылай дәлелденеді.
және жағдайлары да дәл осылай дәлелденеді.
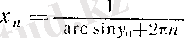 Мысалдар. 1.
Мысалдар. 1.
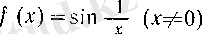 функциясы үшін [-1, +1] сегменті
функциясы үшін [-1, +1] сегменті
 функциясының 0 нүктесіндегі дербес шектер жиыны болады.
функциясының 0 нүктесіндегі дербес шектер жиыны болады.
Расында да,
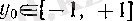 болса, онда
болса, онда
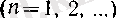 тізбегі үшін
тізбегі үшін
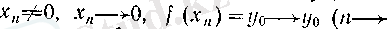
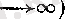 , яғни у
о
саны
f
функциясының 0 нүктесіндегі дербес шегі.
, яғни у
о
саны
f
функциясының 0 нүктесіндегі дербес шегі.
2.
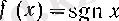 функциясының 0 нүктесіндегі дербес шектер жиыны 1 және -1 сандарынан құрылған екі элементті жиын болады.
функциясының 0 нүктесіндегі дербес шектер жиыны 1 және -1 сандарынан құрылған екі элементті жиын болады.
3.
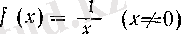 функциясының 0 нүктесіндегі дербес шектер жиыны
функциясының 0 нүктесіндегі дербес шектер жиыны
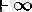 . және
. және
 ақырсыз сандарынан құрылған
ақырсыз сандарынан құрылған
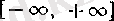 сегментінің екі элементті жиыншасы болады.
сегментінің екі элементті жиыншасы болады.
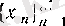 Кез келген функцияның кемінде бір дербес шегі бар болады. Расында да,
а
нақты саны
X
жиынының шектік нүктесі болғандықтан, (1) шарттарын қанағаттандыратын тізбегі табылады. Дәл осы тізбекке сәйкес
Кез келген функцияның кемінде бір дербес шегі бар болады. Расында да,
а
нақты саны
X
жиынының шектік нүктесі болғандықтан, (1) шарттарын қанағаттандыратын тізбегі табылады. Дәл осы тізбекке сәйкес
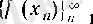 тізбегінің Больцано - Вейерштрасс теоремасы бойынша белгілі бір
тізбегінің Больцано - Вейерштрасс теоремасы бойынша белгілі бір
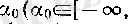
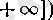 санына ұмтылатын
санына ұмтылатын
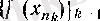 тізбекшесібар болады.
тізбекшесібар болады.
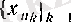 тізбегі
тізбегі
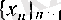 тізбегінің тізбекшесі болады, сондықтан ол (1) -дсгі көрестілген шарттарды қанағаттандырады.
тізбегінің тізбекшесі болады, сондықтан ол (1) -дсгі көрестілген шарттарды қанағаттандырады.
Сонымен,
 функциясының
а
нүктесінде
а
о
-ға тең дербес шегі бар болады.
функциясының
а
нүктесінде
а
о
-ға тең дербес шегі бар болады.
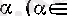 Әрине,
Әрине,
 функциясының
а
нүктесінде шегі бар және
функциясының
а
нүктесінде шегі бар және
 санына тең болуы үшін оның дербес шектер жиыны құрамында тек қана сол а саны болатын бір элементті жиын болуы қажетті және жеткілікті.
санына тең болуы үшін оның дербес шектер жиыны құрамында тек қана сол а саны болатын бір элементті жиын болуы қажетті және жеткілікті.
Бұл дербес шек пен шектің тізбектер тіліндегі анықтамаларынан айқын түрде шығады.
2. 2 Функцияның жоғарғы және төменгі шектері
Енді тізбек жағдайындағыдай, функция үшін дербес шектер жиынының ең үлкен және ең кіші элементтері бар болатынын дәлелдейік.
Алдымен негізгі жағдай - локальді шенелген функцияларды қарастырайық.
Т е о р е м а.
 функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын.
функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын.
Егер
 функциясы
а
нүктесінде локальді шенелген болса, онда
а
нүктесінде
функциясы
а
нүктесінде локальді шенелген болса, онда
а
нүктесінде
 функциясының ең үлкен және ең кіші дербес шектері бар болады да сәйкес мына
функциясының ең үлкен және ең кіші дербес шектері бар болады да сәйкес мына
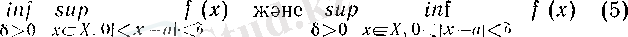
нақты сандарына тең болады.
Дәлелдеуі. (5) -тегі өрнектерді былай түсіну керек:
 функциясы
а
нүктесінде локальді шенелген болғандықтан,
функциясы
а
нүктесінде локальді шенелген болғандықтан,

 шарттарын қанағаттандыратын барлық
х
сандары үшін
шарттарын қанағаттандыратын барлық
х
сандары үшін
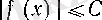 (6)
(6)
теңсіздігі орындалатын
 және
С
оң сандары табылады. Егер әрбір
және
С
оң сандары табылады. Егер әрбір
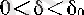 үшін анықтама бойынша
үшін анықтама бойынша
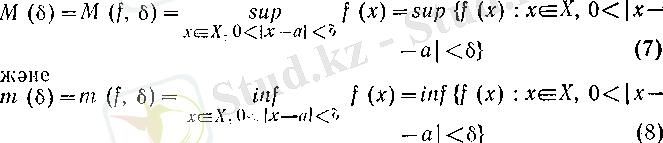
болса, онда
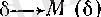 және
және
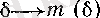 сәйкестіктерінің әр-қайсысы
сәйкестіктерінің әр-қайсысы
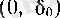 интервалында анықталған функция болады, өйткені: біріншіден, әpбip сандар жиынының тек қана бір супремумы мен тек қана бір инфимумы болады; екіншіден, (6) бойынша
интервалында анықталған функция болады, өйткені: біріншіден, әpбip сандар жиынының тек қана бір супремумы мен тек қана бір инфимумы болады; екіншіден, (6) бойынша
 (9)
(9)
яғни
М
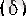 мен
т
(б) -нақты сандар.
мен
т
(б) -нақты сандар.
М
(6) және
т
(6) функциялары
Бәрдің
сәйкес
жоғарғы
және
төменгі функциялары
деп аталады. δ азайған сайын, (7) және (8) анықтамаларындағы супремум мен инфимум анықталған жиын тарыла түседі, демек, 8 (I тарау, § 4) -пункттегі 2-теорема бонышна
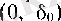 интервалында
М
(б) -кемімейтін, ал
m
(δ) өспейтін функция болады. Сондықтан, (9) және § 5-тегі монотонды функцияның шегі туралы теорема бойынша
интервалында
М
(б) -кемімейтін, ал
m
(δ) өспейтін функция болады. Сондықтан, (9) және § 5-тегі монотонды функцияның шегі туралы теорема бойынша
 болғанда
М
(б) және
т
(δ) функцияларының нақты шектері бар болады да,
болғанда
М
(б) және
т
(δ) функцияларының нақты шектері бар болады да,
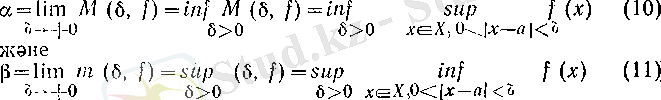
теңдіктері орындалады. (10) -дағы a саны
 функциясының
a
нүктесіндегі дербес шектерінің ең үлкені екенін көрсетейік.
функциясының
a
нүктесіндегі дербес шектерінің ең үлкені екенін көрсетейік.
Алдымен
a
санының өзі дербес шек болатынын дәлелдейік. Дербес шектің анықтамасындағы
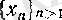 тізбегін былай құрайық: (7) бойынша әрбір оң бүтін
п
саны үшін
тізбегін былай құрайық: (7) бойынша әрбір оң бүтін
п
саны үшін
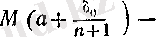
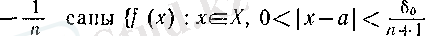 жиынының жоғарғы шекарасы бола алмайды, демек,
жиынының жоғарғы шекарасы бола алмайды, демек,
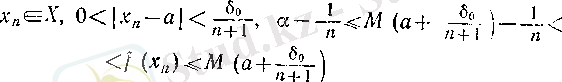 (12)
(12)
теңсіздіктерін қанағаттандыратын
х
п
саны табылады. Бұдан
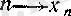 тізбегі үшін (4) шарттарының орындалуы айқын. (10) мен шектің тізбектер тіліндегі анықтамасы бойынша
тізбегі үшін (4) шарттарының орындалуы айқын. (10) мен шектің тізбектер тіліндегі анықтамасы бойынша
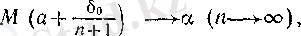
демек, (12) бойынша (3 ІІІ тарау, § 2) -пункттегі 6-теореманы қараңыз)
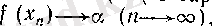 , яғни, расында да,
а
саны
f
функциясының
а
нүктесіндегі дербес шегі болады.
, яғни, расында да,
а
саны
f
функциясының
а
нүктесіндегі дербес шегі болады.
Енді
а
ең үлкен дербес шек болатының яғни әрбір басқа дербес шек
а
санынан аспайтымын көрсетейік. Сонымен,
у
саны
f
функциясының
а
нүктесіндегі дербес шегі болсын. Онда дербес шектің анықтамасы бойынша (4) шарттарын қанағаттандыратын белгілі бір
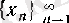 тізбегі үшін
тізбегі үшін
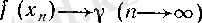 (13)
(13)
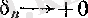 болады.
болады.
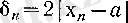 болсын. Онда (4) бойынша
болсын. Онда (4) бойынша
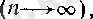 демек, (10) -ды қараңыз)
демек, (10) -ды қараңыз)
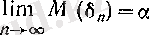 (14)
(14)
Сонымен, (13), (14) және 3 (II тарау, § 2) -пункттегі 5-теорема бойынша өйткені

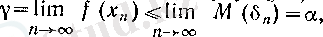
теңсіздігін қанағаттандыратын барлық оң бүтігі
п
сандары үшін
 Теорема толық дәлелденді.
Теорема толық дәлелденді.
Функцияның а нүктесінде ең үлкен дербес шегін жоғарғы шек деп атап,
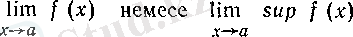 (15)
(15)
символдарымен белгілейді. Дәл солай, функцияның
а
нүктесіндегі ең кіші дербес шегін
төменгі шек
деп атап
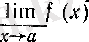 немесе
немесе
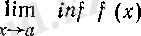 символдарымен белгілейді.
символдарымен белгілейді.
Сөйтіп,
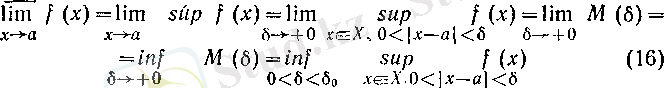
және
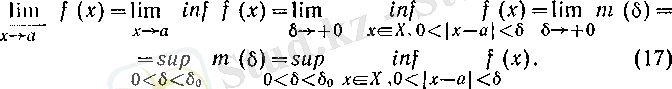
Бұл теңдіктерде алғашқы екі өрнек қалған өрнектердің белгілеулері болады. Қолданылған белгілеулер үшін тізбектер жайында 2 (II тарау, § 5) -пунктте айтылғанды қайталауға болады.
Енді қалған жағдайларды қарастырайық. Егер
 функциясы
а
нүктесінде жоғарыдан локальді шенелмеген болса, онда сол нүктеде
функциясы
а
нүктесінде жоғарыдан локальді шенелмеген болса, онда сол нүктеде
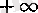 оның дербес шегі болады (әрине, -
оның дербес шегі болады (әрине, -
 ең үлкен дербес шек те болады) .
ең үлкен дербес шек те болады) .
Расында да, функцияның жоғарыдан локальді шенелмегендігінің анықтамасы бойынша әрбір
п
оң бүтін саны үшін (1 (§ 4) -пункттегі (3) анықтамасында
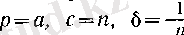 алу керек)
алу керек)
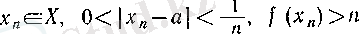
шарттарын қанағаттандыратын
х
п
саны табылады, демек,

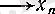 тізбегі үшін
тізбегі үшін
 яғни
яғни
 саны
f
функциясының
а
нүктесіндегі дербес шегі болады. Бұл жағдайда да (15) белгілеулерін сақтайық. (16) теңдіктеріндегі lim немесе
inf
символдарының астында тұрған өрнек
саны
f
функциясының
а
нүктесіндегі дербес шегі болады. Бұл жағдайда да (15) белгілеулерін сақтайық. (16) теңдіктеріндегі lim немесе
inf
символдарының астында тұрған өрнек
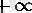 болғанда сол өрнектің бәрі де
болғанда сол өрнектің бәрі де
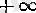 -ке тең болсын деп келіссек, онда
а
нүктесінде жоғарыдан локальді шенелмеген
-ке тең болсын деп келіссек, онда
а
нүктесінде жоғарыдан локальді шенелмеген
 функциясы үшін де (16) теңдіктері орындалады.
функциясы үшін де (16) теңдіктері орындалады.
Дәл осылай, егер
f
функциясы
а
нүктесінде төменнен локальді шенелмеген болса, онда сол нүктеде
 оның дербес шегі болады (әрине,
оның дербес шегі болады (әрине,
 ең кіші дербес шек те болады), тиісті келісімдерді енгізіп, (17) теңдіктерін сақтауға болады.
ең кіші дербес шек те болады), тиісті келісімдерді енгізіп, (17) теңдіктерін сақтауға болады.
2. 3 Нақты функцияның құрылысы туралы
Функцияның тербелісі. «Нақты мәнді функция» деген өте жалпы ұғым болса да, оның әрбір нүктенің қасындағы құрылысы кездейсоқ емес, белгілі бір тәртіпке бағынады екен. Оны жоғарғы және төменгі шектердің анықтамаларының салдары болатын келесі қасиеттерден көруге болады:
f
функциясы
а
нүктесінде локальді шенелген болып,
а
және
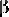 нақты сандары оның сол нүктедегі сәйкес жоғарғы және төменгі шектері болсын.
нақты сандары оның сол нүктедегі сәйкес жоғарғы және төменгі шектері болсын.
1°. Әрбір ɛ оң саны бойынша
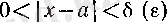 теңсіздігін қанағаттандыратын барлық
теңсіздігін қанағаттандыратын барлық
 сандары үшін
сандары үшін

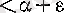 теңсіздіктері орындалатын
теңсіздіктері орындалатын
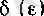 оң саны табылады.
оң саны табылады.
Дәлелдеуі. Инфимумның анықтамасы бойынша әрбір
 саны үшін
саны үшін
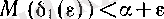 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
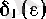 оң саны табылады, демек,
оң саны табылады, демек,
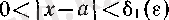 теңсіздіктерін қанағаттандыратын барлық
теңсіздіктерін қанағаттандыратын барлық
 сандары үшін
сандары үшін
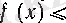
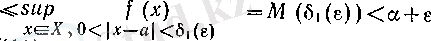 болады. Дәл осылай, (11) мен супремумның анықтамасы бойынша әрбір
болады. Дәл осылай, (11) мен супремумның анықтамасы бойынша әрбір
 саны үшін
саны үшін
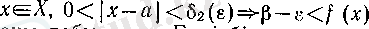 шарты орындалатын
шарты орындалатын
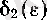 саны табылады. Енді бізге қажетті
саны табылады. Енді бізге қажетті
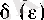 саны ретінде
саны ретінде
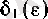 және
және
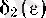 сандарының кішісін алсақ болғаны. Сонымен, 1° дәлелденді.
сандарының кішісін алсақ болғаны. Сонымен, 1° дәлелденді.
2°. Әрбір ɛ және
 оң сандары үшін
оң сандары үшін
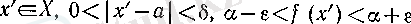 (18)
(18)
шарттарын қанағаттандыратын ақырсыз көп х' сандары бар болады.
Дәлелдеуі. (18) шарттарын қанағаттандыратын кемінде бір
х'
саны бар болатыны дербес шектің
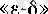 тіліндегі анықтамасынан шығады. Сондықтан, сондай
х'
сандары ақырсыз көп болатынын дәлелдеу қалды. Кері жорысақ, онда белгілі бір
п
он бүтін саны үшін
тіліндегі анықтамасынан шығады. Сондықтан, сондай
х'
сандары ақырсыз көп болатынын дәлелдеу қалды. Кері жорысақ, онда белгілі бір
п
он бүтін саны үшін
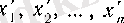 (19)
(19)
сандарынан өзге бірде-бір
х'
саны (18) шарттарын қанағаттандырмайды.
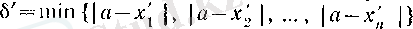 болсын.
болсын.
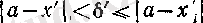 (18) бойынша
(18) бойынша
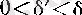 болады.
болады.
 және
және
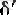 оң сандары үшін дербес шектің
оң сандары үшін дербес шектің
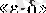 тіліндегі анықтамасы бойынша
тіліндегі анықтамасы бойынша

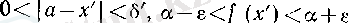 шарттары орындалатын
х'
саны табылады. Әрбір
шарттары орындалатын
х'
саны табылады. Әрбір
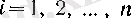 үшін болғандықтан,
үшін болғандықтан,
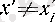
Сонымен, (19) сандарының әрқайсысынай өзге болып, (18) шарттарын қанағаттандыратын
х'
саны табылды (өйткені,
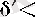 δ ), яғни қайшылыққа келдік. 2° дәлелдепді.
δ ), яғни қайшылыққа келдік. 2° дәлелдепді.
Е с к е р т у. Бұл дәлелдеуде тек қана
а
нақты саны
f
функциясының
а
нүктесіндегі дербес шегі болатыны пайдаланылды, демек, 1-пунктте берілген дербес шектің
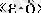 тіліндегі анықтамасында
тіліндегі анықтамасында
 саны табылады» деген сөйлемшені « . . . ақырсыз көп
х'
сандары табылады» деп күшейтуге болады.
саны табылады» деген сөйлемшені « . . . ақырсыз көп
х'
сандары табылады» деп күшейтуге болады.
Бұл ескертуді қолданын,
 нақты саны
f
функциясының дербес шегі болатынын былай айтуға болады.
нақты саны
f
функциясының дербес шегі болатынын былай айтуға болады.
3°. Әрбір ɛ және
 оң сандары үшін
оң сандары үшін
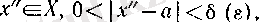
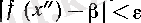 шарттарын қанағаттандыратын ақырсыз көп
х"
сандары бар болады.
шарттарын қанағаттандыратын ақырсыз көп
х"
сандары бар болады.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz