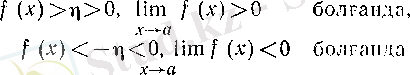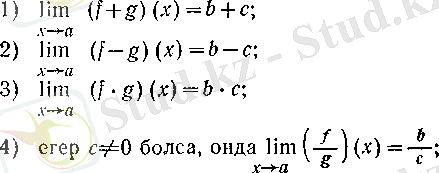Шегі бар функциялардың қасиеттері және монотонды функциялардың шегі


Курстық жұмыс
Тақырыбы: Шегі бар функциялардың қасиеттері. Монотонды функцияның шегі
Мазмұны
Кіріспе. .
1 Шегі бар функциялардың қасиеттері . . .
1. 1 Функцияның шегі. Функцияның нүктедегі шегі . . .
1. 2 Функцияның локальды шенелгендігі . . .
1. 3 Функцияның таңбасы сақталуы туралы теорема . . .
1. 4 Шек және арифметикалық амалдар . . .
1. 5 Күрделі функцияның шегі . . .
1. 6 Функцияның бір ғана нақты шегі болуы туралы теорема . . .
2 Монотонды функцияның шегі . . .
2. 1 Монотонды функция . . .
2. 2 Монотонды функцияның шегі. Коши критерийі . . .
2. 3 Функцияның монотонды болуының белгілері . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі . . .
Қосымша . . .
3
4
4
7
8
9
11
15
17
17
18
21
26
27
28
Кіріспе
Айталық, f(x) функциясы
а
нүктесінің қайсыбір маңайында, мүмкін сол нүктенің өзінен басқа, анықталған болсын. Егер
а
-ға жинақталатын кез келген аргументтін мәндерінің
х
n
 а
,
а
,
 тізбегі үшін функцияның сәйкес мәндерінің f(x
n
),
тізбегі үшін функцияның сәйкес мәндерінің f(x
n
),
 тізбегі
В
санына жинақталса, онда
В
саны f(x) функциясының
а
нүктесіндегі
шегі
деп аталады (немесе
х а-ға
ұмтылғандағы
) .
тізбегі
В
санына жинақталса, онда
В
саны f(x) функциясының
а
нүктесіндегі
шегі
деп аталады (немесе
х а-ға
ұмтылғандағы
) .
Бұл жағдайда
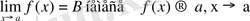 деп жазады.
деп жазады.
Қысқаша, егер
а
-ға жинақталатын кез келген аргументтін мәндерінің
х
n
 а
,
а
,
 тізбегі үшін
тізбегі үшін
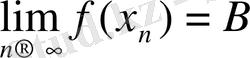 болса, онда
болса, онда
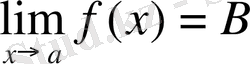 болады.
болады.
1 Мысал:
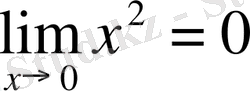 болатының дәлелдеу керек.
болатының дәлелдеу керек.
Δ Аргуметтін мәндерінің кез келген нөлге ұмтылатын
х
n
 0
,
0
,
 тізбегін, яғни,
тізбегін, яғни,
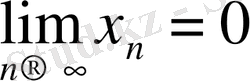 болған жағдайын қарастырайық. Онда, f(x) =x
2
, болғандықтан,
болған жағдайын қарастырайық. Онда, f(x) =x
2
, болғандықтан,
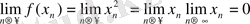 болады.
болады.
Сондықтан,
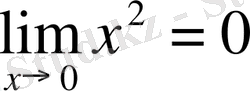
2 Мысал:
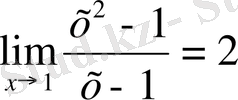 болатының дәлелдеу керек.
болатының дәлелдеу керек.
Δ Аргуметтін мәндерінің кез келген бірге ұмтылатын
х
n
 1
,
1
,
 тізбегін, яғни,
тізбегін, яғни,
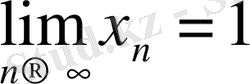 болған жағдайын қарастырайық. Онда, f(x) =
болған жағдайын қарастырайық. Онда, f(x) =
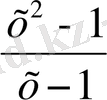 , болғандықтан,
, болғандықтан,
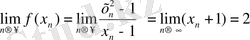 болады.
болады.
Сондықтан,
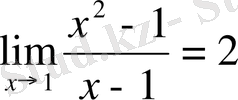
Курстық жұмыстың мақсаты: шегі бар функциялардың қасиеттерін және монотонды функцияның шеін зерттеу.
Міндеттері:
- шегі бар функциялардың қасиеттерін зерттей отырып, функцияның шегін, функцияның нүктедегі шегін және функцияның локальды шенелгендігі зерттеу;
- функцияның таңбасы сақталуы туралы теоремасын қарастыру;
- шек және арифметикалық амалдар мен күрделі функцияның шегін зерттеу;
- функцияның бір ғана нақты шегі болуы туралы теоремасын қарастыру;
- монотонды функцияның шегін, функцияның монотонды болуының белгілерін ашу.
Құрылымы: курстық жұмыс кіріспеден, негізгі бөлімдегі екі тарау мен жеті параграфтан, қорытынды мен қолданылған әдебиеттер тізімінен тұрады.
1 Шегі бар функциялардың қасиеттері
1. 1 Функцияның шегі. Функцияның нүктедегі шегі
Шектің жалғыз болуы туралы теорема.
Теорема: Функцияның нүктедегі бір ғана шегі болады.
ٱ х=а нүктесінде f(x) функцияның екі әр түрлі А және В шектері бар болсын.
Шектің анықтамасына сәйкес аргументтің мәндерінің кез келген
х
n
 а
, және
а
, және
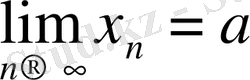 болатын х
n,
болатын х
n,
 тізбегі үшін:
тізбегі үшін:
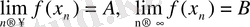
Тізбетің шегі жалғыздығы бойынша А=В теңдігіне келеміз. Бұл функцияның екі әртүрлі шектері бар деген болжамымызға қарама-қайшылық әкеледі. Сондықтан, функцияның нүктеде тек бір ғана шегі бар болады.
Шектер туралы теоремалар.
Теорема 1: Функциялардың қосындысының (айырмасының) шегі олардың шектерінің қосыныдысына (айырмасына) тең:
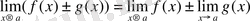
Теорема 2: Функциялардың көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең:
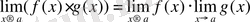
Теорема 3: Екі функциялардың бөліндісінің шегі олардың шектерінің бөліндісіне тең:
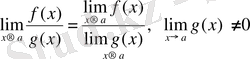
ٱ
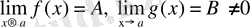 болсын. Онда функцияның нүктедегі шегінің анықтамасы бойынша кез келген
х
n
болсын. Онда функцияның нүктедегі шегінің анықтамасы бойынша кез келген
х
n
 а
, және
а
, және
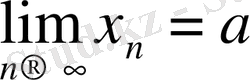 болатын аргументтің мәндерінің х
n
тізбегі үшін
болатын аргументтің мәндерінің х
n
тізбегі үшін
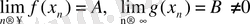 болады.
болады.
Ақырғы теңдіктерді және жинақталатын тізбектердің бөліндісінің шегі туралы теореманы пайдалана отырып келесі теңдікке келеміз:
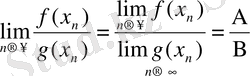
Осыдан,
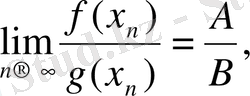 яғни,
яғни,
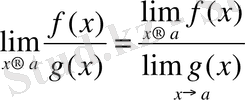 екені шығады.
екені шығады.
1 және 2 теоремалар дәл солай дәлелденеді.
Салдар: Тұрақты көбейткішті шек таңбасының сыртына шығаруға болады:
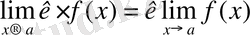
Терема 4: Егер
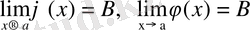 болса және
а
нүктесінің қайсыбір маңаында
болса және
а
нүктесінің қайсыбір маңаында
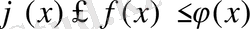 теңдіктері орындалса, онда
теңдіктері орындалса, онда
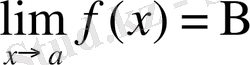 болады.
болады.
1 Мысал:
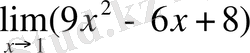 -ті табу керек.
-ті табу керек.
Δ Шектер туралы теоремаларды қолданып келесіге келеміз:
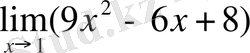
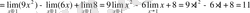
2 Мысал:
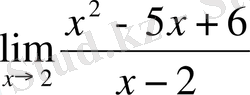 -ті табу керек.
-ті табу керек.
Δ Мұнда бөлімнің шегі нөлге тең, сондықтан бөліндінің шегі туралы теореманы қолдануға болмайды. Алымын көбейткіштерге жіктейік:
Х 2 -5х+6=(х-3) (х-2) .
2 нүктесіндегі шекті тапқанда тек х
 2 қарастырылғандықтан х-2-ге қысқартуға болады, сонда
2 қарастырылғандықтан х-2-ге қысқартуға болады, сонда
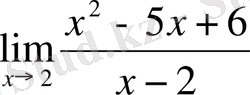
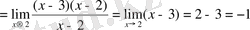
Ескерту: осы мысалда х=2 нүктесінде бөлшектің алымы мен бөлімі нөлге айналады. Мұндай жағдайларда
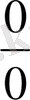 түріндегі анықталмағандығы бар деп айтады, ал шекті табуды
түріндегі анықталмағандығы бар деп айтады, ал шекті табуды
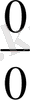 түріндегі анықталмағандығын ашу деп айтады.
түріндегі анықталмағандығын ашу деп айтады.
Біржақты шектер.
Егер шекті тапқанда
х
-тің мәндерін тек
а
нүктесінің сол жағынан ғана қарастырсақ, онда шек
солжақтық
деп аталады да былай белгіленеді
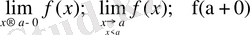 .
.
Егер шекті тапқанда х-тің мәндерін тек
а
нүктесінің оң жағынан ғана қарастырсақ, онда шек
оңжақтық
деп аталады да былай белгіленеді
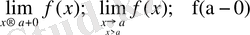 .
.
Солжақтық және оңжақтық шектер біржақтық шектер деп аталады, ал шек екіжақтық деп аталады.
Анықтамалардан, егер f(x) функциясының х
0
нүктесінде шегі бар болса және
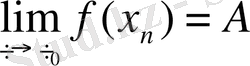 болса, онда біржақтық f(x
0
+0) және f(x
0
-0) шектері де бар болады да f(x
0
+0) = f(x
0
-0) = А болады.
болса, онда біржақтық f(x
0
+0) және f(x
0
-0) шектері де бар болады да f(x
0
+0) = f(x
0
-0) = А болады.
Сонымен, f(x) функциясының х 0 нүктесіндегі шегін анықтау үшін келесі үш шарттың орындалуын тексеру жеткілікті:
- солжақтық шектің бар болуы;
- оңжақтық шектің бар болуы;
- біржақтық шектерінің тең өзара болуы;
1 Мысал: f(x)
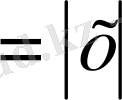 Equation. 3 функциясының х
Equation. 3 функциясының х
 0 шегін табу керек.
0 шегін табу керек.
Δ Берідген функция сандық түзудің барлық бойында анықталған (1 сурет) . Барлық х<0 теңсіздігін қанағаттандыратын
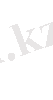 х үшін f(x) =
х үшін f(x) =
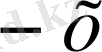 болғандықтан
болғандықтан
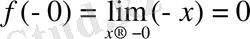 болады. Дәл солай
болады. Дәл солай
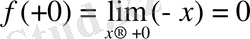 болады.
болады.
Сонымен, f(+0) = f(-0) = 0.
Біржақтық шектер нөл нүктесінде өзара тең болғандықтан f(x) функциясының нөл нүктесінде бар болады да олардың ортақ мәніне тең болады, яғни,
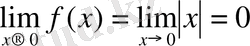
Функцияның шексіздіктегі шегі. Функцияның
 шегі туралы.
шегі туралы.
f(x) функциясы сандық түзуінің бойында анықталған болсын. Егер
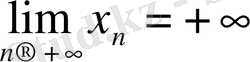 болатын кез келген х
n
тізбегі үшін
болатын кез келген х
n
тізбегі үшін
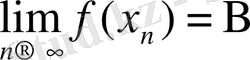 болса, онда В саны f(x) функциясының
болса, онда В саны f(x) функциясының
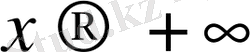 шегі деп аталады.
шегі деп аталады.
Бұл жағдайда
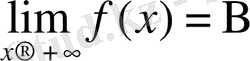 деп жазады. Дәл солай, егер
деп жазады. Дәл солай, егер
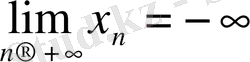 болатын кез келген х
n
тізбегі үшін
болатын кез келген х
n
тізбегі үшін
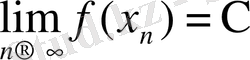 болса, онда
болса, онда
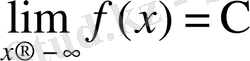 болады.
болады.
Анықтама: Егер
х
n
 а
және
а
және
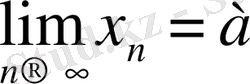 болатын кез келген аргументтін мәндерінің
х
n
тізбегі үшін
болатын кез келген аргументтін мәндерінің
х
n
тізбегі үшін
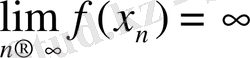 болса, онда
f(x) функциясының а
нүктесіндегі шегі шексіздік
болады дейді де
болса, онда
f(x) функциясының а
нүктесіндегі шегі шексіздік
болады дейді де
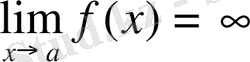 деп жазады.
деп жазады.
Егер бұл анықтамада
х
n
 а
шартын
х
n
а
шартын
х
n
 а
шартына ауыстырса, онда функцияның сол жақтық шексіз
а
нүктесіндегі шегінің анықтамасы шығады.
а
шартына ауыстырса, онда функцияның сол жақтық шексіз
а
нүктесіндегі шегінің анықтамасы шығады.
Мысал:
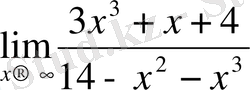 шегін табу керек.
шегін табу керек.
Δ Алым мен бөлімді х 3 -қа бөлеміз:
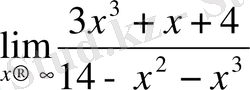
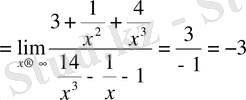
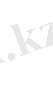
Ескерту: бұл есепте
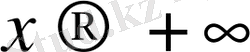 алым мен бөлім шексіздікке ұмтылады. Ондай жағдайларда
алым мен бөлім шексіздікке ұмтылады. Ондай жағдайларда
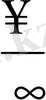 түріндегі анықталмағандығы бар дейді де шекті табуды
түріндегі анықталмағандығы бар дейді де шекті табуды
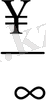 түріндегі анықталмағандығын ашу деп айтады.
түріндегі анықталмағандығын ашу деп айтады.
Егер
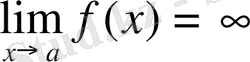 болса, онда f(x) функциясы
болса, онда f(x) функциясы
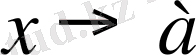 шексіз (ақырсыз) үлкен
деп аталады. Егер де
шексіз (ақырсыз) үлкен
деп аталады. Егер де
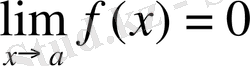 болса, онда f(x) функциясы
болса, онда f(x) функциясы
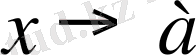 шексіз (ақырсыз) кіші
деп аталады. Дәл солай
шексіз (ақырсыз) кіші
деп аталады. Дәл солай
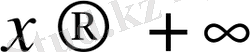 ,
,
 шексіз (ақырсыз) үлкен және шексіз кіші функциялар да анықталады.
шексіз (ақырсыз) үлкен және шексіз кіші функциялар да анықталады.
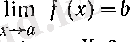 1. 2 Функцияның локальды шенелгендігі
1. 2 Функцияның локальды шенелгендігі
f
функциясы
X
жиынында анықталып,
а
нақты саны сол жиынның шектік нүктесі болсын. Егер
f
функциясының
а
нүктесінде нақты мәнді шегі бар болса. онда
а
-ның белгілі бір ойылған маңайында
f
функциясы шенелген болады. Расында да,
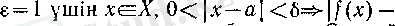
 болсын. Онда шектің анықтамасы бойынша шарты орындалатын
болсын. Онда шектің анықтамасы бойынша шарты орындалатын
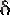 оң саны табылады. Сондай
х
сандары үшін
оң саны табылады. Сондай
х
сандары үшін
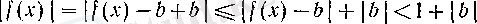 (1)
(1)
болады, яғни f функциясы а нүктесінің ойылған δ маңайында шенелген болады.
Бұл жағдайда « f функциясы а нүктесінде локальді шенелген» дейді.
Сонымен, дәлелденген тұжырымды басқаша былай айтуға болады: егер f функциясының а нүктесінде нақты мәнді шегі бар болса, онда f сол нүктеде локальді шенелген болады.
Бұл теорема шектің жалпы жағдайында да орындалады:
Теорема. Егер
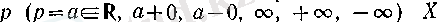 жиынының шектік нүктесі болып, сол жиында анықталған
жиынының шектік нүктесі болып, сол жиында анықталған
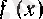 функциясының
х
р
-ға ұмтылғанда нақты мәнді шегі бар болса, онда
f
функциясы
р
нүктесінде локальді шенелген болады, яғни
функциясының
х
р
-ға ұмтылғанда нақты мәнді шегі бар болса, онда
f
функциясы
р
нүктесінде локальді шенелген болады, яғни
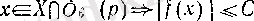 (2)
(2)
шартын қанағаттандыратын
С
және δ оң сандары табылады. Расында да,
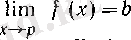 болса, онда шектің анықтамасы бойынша
болса, онда шектің анықтамасы бойынша
 үшін
үшін
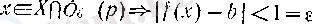 шарты орындалатын δ оң саны табылады. Дәл осы δ мен
шарты орындалатын δ оң саны табылады. Дәл осы δ мен
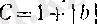 үшін (1) бойынша (2) шарты орындалатыны айқын.
үшін (1) бойынша (2) шарты орындалатыны айқын.
Әрине, f функциясы р-да локальді шенелмегендігі былай анықталады:
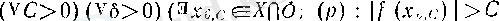 (3)
(3)
яғни, сөзбен айтқанда, р -ның әрбір ойылған маңайында f функциясы шенелмеуі керек.
Мысалы,
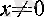 үшін анықталған
үшін анықталған
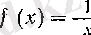 - функциясы әрбір
- функциясы әрбір
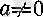 нүктесінде локальді шенелген, өйткені
нүктесінде локальді шенелген, өйткені
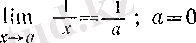 нүктесінде локальді шенелмеген, өйткені әрбір
нүктесінде локальді шенелмеген, өйткені әрбір
 және 0
және 0
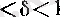 үшін
үшін
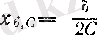 болғанда
болғанда
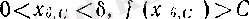 болады.
болады.
Егер функцияның локальді шенелуінің анықтамасында «шенелген» деген сөзді «жоғарыдан шенелген» немесе «төменнен шенелген» деген сөздерге өзгертсек, онда функцияның сәйкес жоғарыдан және төменнен локальді шенелген болуының анықтамаларына келеміз. Мысалы, егер
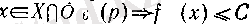 шартын канағаттандыратын
С
және
шартын канағаттандыратын
С
және
 нақты сандары табылса, онда
f
функциясы
р
нүктесінде
жоғарыдан локальді шенелген
дейді.
нақты сандары табылса, онда
f
функциясы
р
нүктесінде
жоғарыдан локальді шенелген
дейді.
Әрине, f функциясы р -да жоғарыдан локальді шенелмегендігі былай анықталады:
 (4)
(4)
р = а + 0 және р = а - 0 болғанда, әдеттегідей, ұғыммың аталуына оң және сол жақты деген сөздер қосылады.
1. 3 Функцияның таңбасы сақталуы туралы теорема
Т е о р е м а. Егер
X
жиынында анықталған
f
функциясының
 нүктесінде ноль емес нақты мәнді шегі болса, онда функцияның мәндері де
а
нүктесінің белгілі бір маңайында шегінің таңбасын сақтайды.
нүктесінде ноль емес нақты мәнді шегі болса, онда функцияның мәндері де
а
нүктесінің белгілі бір маңайында шегінің таңбасын сақтайды.
Дәлірек айтқанда, әрбір
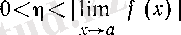 саны бойынша барлық
саны бойынша барлық
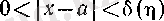 теңсіздігін қанағаттандыратын
теңсіздігін қанағаттандыратын
 сандары үшін келесі шарттар
сандары үшін келесі шарттар
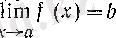 орындалатындай
орындалатындай
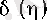 оң саны табылады.
оң саны табылады.
Д ә л е л д е у і. болсын, онда
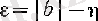 оң сан болады.
оң сан болады.
Шектің анықтамасы бойынша дәл осы ɛ үшін
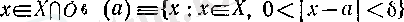 (5)
(5)
болғанда
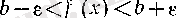 теңсіздігі орындалатын
теңсіздігі орындалатын
 саны табылады. Ендеше, (5) шартын қанағаттандыратын әрбір
х
сандары үшін b > 0 болғанда
саны табылады. Ендеше, (5) шартын қанағаттандыратын әрбір
х
сандары үшін b > 0 болғанда
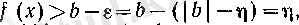 ал b<0 болғанда
ал b<0 болғанда
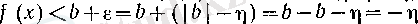 теңсіздіктері орындалады. Теорема дәлелденді.
теңсіздіктері орындалады. Теорема дәлелденді.
1. 4 Шек және арифметикалық амалдар
Мақты мәнді функциялар үшін арифметикалық амалдар 3 (I тарау, § 2) -пунктте анықталған еді. Енді олардың шектері туралы не айтуға болатынын зерттейік.
Алдымен сол анықтамаларды еске түсірейік.
X
сандар жиынында
f
жонс
g
функциялары берілсін.
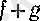 символымен әрбір
Х
-тан алынған
х
саны үшін
символымен әрбір
Х
-тан алынған
х
саны үшін
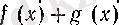 сәйкес қоятын функция белгіленеді. Дәл осылай екі функцияның айырымы
f - g,
көбейтіндісі
f
•
g,
бөліндісі
сәйкес қоятын функция белгіленеді. Дәл осылай екі функцияның айырымы
f - g,
көбейтіндісі
f
•
g,
бөліндісі
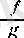 анықталады (әрине, соңғы анықтамада барлық
анықталады (әрине, соңғы анықтамада барлық
 үшін
үшін
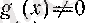 шартын қою қажет) . Егер барлық
шартын қою қажет) . Егер барлық
 үшін
үшін
 теңсіздігі орындалса, оны былай белгілейді:
теңсіздігі орындалса, оны былай белгілейді:

Теорема. а нақты саны X сандар жиынының шектік нүктесі болсын және Х-те анықталған f пен g функцияларының нақты мәнді шектері бар болып,
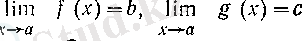 (6)
(6)
теңдіктері орындалсын. Сонда
5) егер
а
-ның белгілі бір ойылған маңайында
 болса, онда
болса, онда
 болады.
болады.
Дәлелдеуі. Алдымен 1) -4) дәлелдейік.
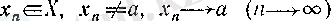 (7)
(7)
шарттары орындалатын әрбір
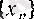 тізбегі үшін 4 (II тарау, § 2) -пункттегі 7-теорема бойынша келесі
тізбегі үшін 4 (II тарау, § 2) -пункттегі 7-теорема бойынша келесі
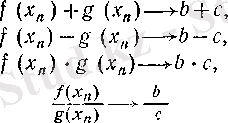 (8)
(8)
шарттары орындалады, өйткені (6) теңдіктері шектің тізбектер тіліндегі анықтамасы бойынша
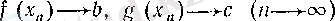 (9)
(9)
болатынын бейнелейді. Сонымен, шектің тізбектер тіліндегі анықтамасы бойынша (7) және (8) шарттарынан 1) -4) теңдіктері шығады.
Енді 5) -ті дәлелдейік. (7) шарттарын қанағаттандыратын
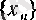 тізбегін бекітейік. Теореманың 5) -тегі шарты бойынша
тізбегін бекітейік. Теореманың 5) -тегі шарты бойынша
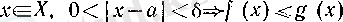 (10)
(10)
шарты орындалатын δ оң саны бар болды. Ал
 болғандықтан, тізбектің шегінің анықтамасы бойынша дәл осы δ саны үшін
болғандықтан, тізбектің шегінің анықтамасы бойынша дәл осы δ саны үшін
 болғанда
болғанда
 теңсіздіктері орындалатып
К
> 0 саны табылады. Бұдан (10) бойынша барлық
теңсіздіктері орындалатып
К
> 0 саны табылады. Бұдан (10) бойынша барлық
 үшін
үшін
 болады.
болады.
Соңғы теңсіздікте
 болғанда шекке көшсек, онда (9) шарттары мен керекті теорема бойынша дәлелдеу керек болатын
болғанда шекке көшсек, онда (9) шарттары мен керекті теорема бойынша дәлелдеу керек болатын
 теңсіздігіне келеміз.
теңсіздігіне келеміз.
Ескерту. Әрине, 1) мен 3) теңдіктері екі функция үшін ғана емес, кез келген ақырлы қосынды мен көбейтінді үшін де орындалады (оны 1) мен 3) бойынша математикалық индукция әдісін қолданып дәлелдеуге болады) .
1-салдар. Әрбір
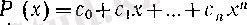 көпмүшелігі мен әрбір
а
нақты саны үшін
көпмүшелігі мен әрбір
а
нақты саны үшін
(11)
болады.
Расында да,
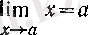 болуы айқын, демек, теорема және ескерту бойынша әрбір оң бүтін
k
саны үшін
болуы айқын, демек, теорема және ескерту бойынша әрбір оң бүтін
k
саны үшін
... жалғасы
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz