Шенелген жиындар және олардың қасиеттері


Курстық жұмыс
Тақырыбы: Шенелген жиындар және олардың қасиеттері
Мазмұны
Кіріспе . . .
1 Жиындар теориясы . . .
1. 1 Жиын және оның элементтері. Ішкі жиын . . .
1. 2 Жиындардың қиылысуы. Жиындардың бірігуі . . .
2 Шенелген жиындар және олардың қасиеттері . . .
2. 1 Ақырсыз сандар . . .
2. 2 Шенелген жиындар. Жоғарғы және төменгі шекаралар . . .
2. 3 Санды жиынның ең үлкен және ең кіші элементтері . . .
2. 4 Сегмент пен интервал.
2. 5 Шенелген тізбектер. .
Қорытынды . . .
Қолданылған әдебиеттердің тізімі . . .
Қосымша . . .
3
4
4
5
8
8
9
10
11
13
17
18
19
Кіріспе
Шенелген жиын - кезкелген х элементі үшін х≤В теңсіздігін қанағаттандыратын В саны бар болатын Е={х} жиыны.
 сандар жиыны берілсін. Егер барлық
сандар жиыны берілсін. Егер барлық
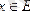 үшін
үшін
 теңсіздігі орындалатын
теңсіздігі орындалатын
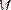 нақты саны табылса, онда
нақты саны табылса, онда
 жиынын жоғарыдан шенелген деп, ал
жиынын жоғарыдан шенелген деп, ал
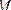 санын
санын
 жиынының жоғарғы шекарасы деп атайды.
жиынының жоғарғы шекарасы деп атайды.
Яғни,
 .
.
Әрине, егер
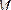 саны
саны
 жиынының жоғарғы шекарасы болса, онда одан үлкен кез келген
жиынының жоғарғы шекарасы болса, онда одан үлкен кез келген
 саны да сол жиынның жоғарғы шекарасы болады.
саны да сол жиынның жоғарғы шекарасы болады.
Анықтама. Егер барлық
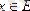 үшін
үшін
 теңсіздігі орындалатын
теңсіздігі орындалатын
 нақты саны табылса, онда
нақты саны табылса, онда
 жиынын төменнен шенелген деп, ал
жиынын төменнен шенелген деп, ал
 санын
санын
 жиынының төменгі шекарасы деп атайды.
жиынының төменгі шекарасы деп атайды.
Яғни,
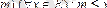 .
.
Егер
 жиыны жоғарыдан да, төменнен де шенелген болса, яғни
жиыны жоғарыдан да, төменнен де шенелген болса, яғни
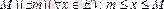 шарты орындалса, онда
шарты орындалса, онда
 -ні шенелген не шектелген жиын деп атайды.
-ні шенелген не шектелген жиын деп атайды.
Анықтама бойынша әрбір
 нақты саны үшін
нақты саны үшін
 болғандықтан, кез келген сандар жиыны үшін
болғандықтан, кез келген сандар жиыны үшін
 жоғары шекара, ал
жоғары шекара, ал
 төменгі шекара деп айтуға болады.
төменгі шекара деп айтуға болады.
Мысалдар.
1.
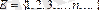 жиыны ақырсыз, төменнен шенелген жиын. Оның төменгі шекарасы
жиыны ақырсыз, төменнен шенелген жиын. Оның төменгі шекарасы
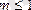 сандары.
сандары.
2.
 жиыны ақырсыз, жоғарыдан шенелген жиын. Оның жоғарғы шекарасы
жиыны ақырсыз, жоғарыдан шенелген жиын. Оның жоғарғы шекарасы
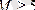 сандары.
сандары.
Курстық жұмыстың мақсаты: шенелген жиындарды және олардың қасиеттерін зерттеу.
Міндеттері:
- жиындар теориясын зерттеу, және оның элементтері, ішкі жиын және жиындардың қиылысуы мен бірігуін қарастырып өту;
2 Шенелген жиындар және олардың қасиеттерін зерттеу.
Курстық жұмыс құрамына келесі пунктер кіреді:
- кіріспе;
- негізгі екі тарау;
- қорытынды;
- қолданылған әдебиеттер тізімі;
- қосымша.
1 Жиындар теориясы
1. 1 Жиын және оның элементтері. Ішкі жиын
Математикада XIX ғасырдың екінші жартысында жиын ұғымы пайда болды. Жиын ұғымының математикаға енуі жиын теориясын қалыптастырды. Жиын теориясының негізін қалаушы неміс математигі Георг Кантор (1845-1918) болды.
Белгілі бір ортақ қасиеттерге ие болып, белгілі бір заңдылықпен біріккен нәрселер, объектілер жиын құрайды. Мысалы: аспандағы жұлдыздар жиыны, кітап бетіндегі әріптер жиыны, бөлімі 6 саны болатын дұрыс бөлшектер жиыны т. с. с.
Жиындар элементтерден құралады. Жиындардың элементтері аталып беріледі немесе сол жиын элементтеріне ғана тән қасиет (белгі) көрсетіледі. Жиынды латынның бас әрпімен белгілеп, оның элементтерін фигуралық жақшаның ішіне алып жазу келісілген. Мысалы, “планета” сөзіндегі әріптер жиынын P әрпімен белгілесек, P={а, п, н, л, е, т} немесе P={т, п, н, л, е, а} элементтер ретін әр-түрлі жазуға болады.
Жиындар шектеулі жиын, шектеусіз жиын болып бөлінеді. Мысалы, цифрлар жиыны A - шектеулі жиын, оған 10 элемент енеді. A={0, 1, 2, 3, 4, 5, 6, 7, 8, 9} жиынының элементтер санын көрсетіп жазсақ: n(A) =10. Ал натурал сандар жиыны N - шектеусіз жиын.
Егер a элементі B жиынына тиісті болса, оның жазылуы: a Є B. Оқылуы: “a B жиынының элементі” немесе “a B жиынына тиісті”.
Мысалы, 7 саны натурал сандар жиынына тиісті: 7 Є N.
Егер c элементі A жиынына тиісті болмаса, оның жазылуы: c ¢ A. Оқылуы:”c A жиынына тиісті емес”. Мысалы, 0 саны натурал сандар жиынына тиісті емес: 0 ¢ N.
Егер жиында бірде-бір элемент болмаса, оны бос жиын деп атайды. Бос жиынның белгіленуі: Ø . Мысалы, 74 және 79 сандарының арасындағы жай сандар жиыны - бос жиын. Әріптер жазылмаған дәптер бетіндегі әріптер жиыны - бос жиын.
Егер B жиынының әрбір элементі A жиынына тиісті болса, онда B жиыны A жиынының ішкі жиыны деп аталады.
Мысалы, A={1, 2, 3, 4, 5, 6, 7} жиынындағы жұп сандар жиыны - B={2, 4, 6}. B жиынының әрбір элементі A жиынына тиісті. Белгіленуі: B Є A. Оқылуы: B жиыны - A жиынының ішкі жиыны.
Жиындардың байланыстары мен арақатынастары Эйлер-Венн дөңгелектері арқылы кескінделеді.
Суретте B жиыны A жиынының ішкі жиыны екені Эйлер-Венн дөңгелектері арқылы кескінделген.
Бос жиын кез келген жиынның ішкі жиыны болады. Белгіленуі: Ø Є A. Мұндағы A - қандай да бір жиын.
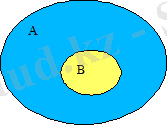
Сурет 1.
Егер екі жиын бірдей элементтерден тұрса, онда олар тең жиындар деп аталады. Мысалы, A={a, b, c}; B={c, a, b}, онда A=B. Оқылуы: A жиыны B жиынына тең.
1. 2 Жиындардың қиылысуы. Жиындардың бірігуі
A жиынына да, B жиынына да тиісті элементтерден ғана тұратын жиынды A және B жиынының қиылысуы деп атайды.
1-есеп. Сыныпта 16 ұл бала бар. Олардың 14-і бос уақытында футбол ойнағанды ұнатады, 9-ы шахмат ойнағанды ұнатады. Бұл ойындарға сыныптағы барлық ұл балалар қатысады. Сыныптағы неше оқушы бос уақытында футбол ойнағанды да, шахмат ойнағанды да ұнатады?
Шешуі: Бос уақытында футбол ойнағанды ұнататын сыныптағы ұлдардың жиыны - A, n(A) =14. Бос уақытында шахмат ойнағанды ұнататын сыныптағы ұлдардың жиыны - B, n(B) =9.
14 + 9 = 23 - бос уақытында футбол ойнағанды ұнататын және шахмат ойнағанды ұнататын сыныптағы ұлдар саны.
23 - 16 = 7 - бос уақытында футбол ойнағанды да, шахмат ойнағанды да ұнататын сыныптағы ұлдар саны.
Сыныптағы футбол ойнағанды да, шахмат ойнағанды да ұнататын ұлдар жиыны
C болсын, онда n(C) =7. Демек, C жиыны - A және B жиындарының қиылысу жиыны, себебі мұндағы әрбір ұл бала A жиынына да, B жиынына да тиісті (ортақ) .
Есептің шешуі Эйлер-Венн дөңгелектерімен былай кескіндейміз.
A ∩ B = C
Әрбір элементі A немесе B жиындарының кем дегенде біреуіне тиісті болатын жиын A және B жиындарының бірігуі деп аталады.
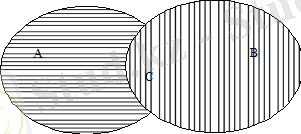
Сурет 2.
2-есеп. Бір топтағы туристердің 10-ы қазақ тілін біледі, 8-і орыс тілін біледі, олардың 3-еуі қазақ тілін де, орыс тілін де біледі. Топта барлығы неше турист бар?
Шешуі: Бір топ туристердің қазақ тілін білетіндердің жиыны - A; n(A) =10.
Орыс тілін білетіндерінің жиыны - B; n(B) =8.
10 + 8 = 18 - топ ішіндегі туристердің қазақ тілін білетіндердің және орыс тілін білетіндердің саны.
18 - 3 = 15 - топ ішіндегі туристер саны.
Топтағы туристер D жиынын құрайды n(D) =15. Демек, D жиыны өзара қиылысып тұрған A және B жиындарының бірігуі болып табылады.
Есептің шешуі Эйлер-Венн дөңгелектері арқылы былай кескіндейміз.
А U B = D
Сурет 3.
3-есеп: Жасыл, қызыл және сары түсті шарлардан тізбе жасалған. Ондағы сары түсті емес шарлар саны 23. Қызыл түсті емес шарлар саны 20. Жасыл түсті емес шарлар саны 15. Тізбеде барлығы неше шар бар? Жасыл түсті шар нешеу? Сары түсті шар нешеу?
Шешуі: Сары түсті емес шарлар - 23, қызыл түсті емес шарлар - 20, жасыл түсті емес шарлар - 15.
23 + 20 + 15 = 58;
58 : 2 = 29;
29 - 15 = 14;
29 - 23 = 6.
Жауабы: барлығы 29, жасыл түсті 14, сары түсті 6.
4-есеп: Қалаға 22 турист келді. Кешкі демалыс кезінде 9 турист драма театрына барғысы келді, 12 турист демалыс паркіне барып дем алғысы келді, ал олардың ішінде 5 турист драма театрына да, демалыс паркіне де барғысы келді. Қалғандары стадионға барып, футбол ойынын көргісі келді. Неше турист стадионға барып, футбол ойынын көргісі келді?
Шешуі: Барлығы - 22 турист, драма театрына - 9 турист, демалыс паркіне - 12 турист. Демалыс паркіне де, драма театрына да - 5 турист.
12 + 9 = 21;
21 - 5 = 16;
22 - 16 = 6.
Жауабы: 6 турист стадионға барды.
2 Шенелген жиындар және олардың қасиеттері
2. 1 Ақырсыз сандар
Көп жағдайларда
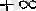 және
және
 символдары пайдалы болады. Бұл символдарды
ақырсыз сандар
деп атаймыз да, келесі шарттар орындалады ден ұйғарамыз:
символдары пайдалы болады. Бұл символдарды
ақырсыз сандар
деп атаймыз да, келесі шарттар орындалады ден ұйғарамыз:
1°. Егер х нақты сан болса, онда
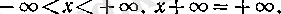
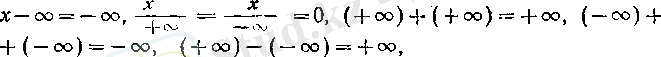
2°. Егер х > 0 болса, онда

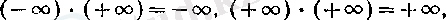
3°. Егер
 болса, онда
болса, онда
 болады.
болады.
Бұл қасиеттер анықтама ретінде алынып отыр, сондықтан дәлелденбейді. Бірақ ілгерідегі 5 (II тарау, § 2) -пунктте оларды белгілі мағынада ақтауға болатынын көрсетеміз.
Бұл кітапта нақты сандар жиыны әрқашанда
R
әрпімен белгіленеді.
 және
және
 сандарымен толықтырылған барлық нақты сандар жиыны R әрпімен белгіленеді.
сандарымен толықтырылған барлық нақты сандар жиыны R әрпімен белгіленеді.
Сонымен,
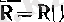
Кейбірденақты сандарды ақырлы caн деп атаймыз.
Сан деп әрқашанда нақты санды атаймыз.
2. 2 Шенелген жиындар. Жоғарғы және төменгі шекаралар
Бұл ұғымдар ілгеріде өте маңызды болады. Сондықтан, алдымен қолданатын терминологияны дәлдеп алайық.
х
пен
у
нақты сандары берілсін.
 қатынасы орындалғанда
х
саны
у
санынан
үлкен
немесе
у
саны
х
санынан
кіші
дейміз.
қатынасы орындалғанда
х
саны
у
санынан
үлкен
немесе
у
саны
х
санынан
кіші
дейміз.
 қатынасы орындалғанда, яғни
х=у
әлде
х>у
болғанда,
х
саны
у
санынан
кіші емес, у
саны
х
санынан
аспайды
немесе
у
саны
х
санынан
үлкен емес
дейміз. Егер
х
> 0 болса, онда
х
оң сан;
х
<0 болса, онда
х
теріс сан;
қатынасы орындалғанда, яғни
х=у
әлде
х>у
болғанда,
х
саны
у
санынан
кіші емес, у
саны
х
санынан
аспайды
немесе
у
саны
х
санынан
үлкен емес
дейміз. Егер
х
> 0 болса, онда
х
оң сан;
х
<0 болса, онда
х
теріс сан;
 болса, онда
х
теріс емес caн;
болса, онда
х
теріс емес caн;
 болса, онда
х
оң емес сан дейді.
болса, онда
х
оң емес сан дейді.
Нақты сандардан құрылған жиынды
сандар жиыны
дейді. Мынаны айрықша ескертеміз: сандар жиынына
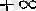 пен
пен
 ақырсыз сандары ешқашанда кірмейді.
ақырсыз сандары ешқашанда кірмейді.
 жазуы
Е
нақты сандар жиынды екенін көрсетеді.
жазуы
Е
нақты сандар жиынды екенін көрсетеді.
Е
сандар жиыны берілсін. Егер барлық
 үшін
үшін
 теңсіздігі орындалатын а нақты саны табылса, онда
Е
жиынын жоғарыдан шенелген не шектелген деп, ал a санын
Е
жиынының
жоғарғы шекарасы
деп атайды.
теңсіздігі орындалатын а нақты саны табылса, онда
Е
жиынын жоғарыдан шенелген не шектелген деп, ал a санын
Е
жиынының
жоғарғы шекарасы
деп атайды.
Әрине, егер a саны
Е
жиынының жоғарғы шекарасы болса, онда одан үлкен кез келген
 саны да жоғарғы шекара болады.
саны да жоғарғы шекара болады.
Кванторлар арқылы Е жиынының жоғарыдан шенелгендігі былай жазылады.
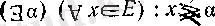 (1)
(1)
Енді қарама-қарсы тұжырым құру ережесін қолдансақ, онда (1) тұжырымы
 түрінде жазылады, яғни әрбір a нақты саны үшін
Е
жиынынан одан үлкен
х
саны табылса, онда
Е
жоғарыдан шенелмеген не шектелмеген жиын деп аталады.
түрінде жазылады, яғни әрбір a нақты саны үшін
Е
жиынынан одан үлкен
х
саны табылса, онда
Е
жоғарыдан шенелмеген не шектелмеген жиын деп аталады.
Жиынның төменнен шенелгендігі не шектелгендігі дәл осылай анықталады. Барлық
 үшін
үшін
 теңсіздігі орындалатын
теңсіздігі орындалатын
 нақты саны табылуы керек, яғни
нақты саны табылуы керек, яғни
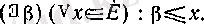 Мұндай
Мұндай
 саны
Е
жиынының
төменгі шекарасы
деп аталады.
саны
Е
жиынының
төменгі шекарасы
деп аталады.
Егер
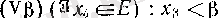 . . . шарты орындалса, яғни әрбір
. . . шарты орындалса, яғни әрбір
 нақты саны үшін одан кіші
Е
жиынының
х
нақты саны үшін одан кіші
Е
жиынының
х
 элементі бар болса, онда
Е төменнен шенелмеген
не шектелмеген жиын болады.
элементі бар болса, онда
Е төменнен шенелмеген
не шектелмеген жиын болады.
Егер
Е
жиыны жоғарыдан да, төменнен де шенелген болса. яғни
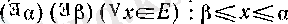 шарты орындалса, онда
Е-ні
шенелген не шектелген жиын деп атайды.
шарты орындалса, онда
Е-ні
шенелген не шектелген жиын деп атайды.
Әрине,
Е
шенелген жиын болуы белгілі бір
 саны мен барлық
саны мен барлық
 үшін
үшін
 теңсіздігі орындалуымен пара-пар (мысалы,
теңсіздігі орындалуымен пара-пар (мысалы,
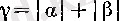 алуға болады) .
алуға болады) .
Енді бірнеше мысалдарды қарастырайық.
1°. Ақырлы жиын әрқашанда шенелген жиып болады, өйткені оның элементтері
х
1
, х
2
. . . ,
х
п
болса, онда
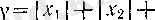
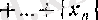 нақты саны үшін
нақты саны үшін
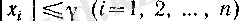 тенсіздігі орындалады.
тенсіздігі орындалады.
2°. Барлық оң бүтін сандардан құрылған Ј жиыны төменнен шенелген, бірақ жоғарыдан шенелмеген.
Расында да, әрбір
 үшін
үшін
 , демек,
Ј
төменнен шенелген жиын; әрбір
а
нақты саны үшін одан үлкен оң бүтін сан табылды, демек,
Ј
жоғарыдан шенелмеген.
, демек,
Ј
төменнен шенелген жиын; әрбір
а
нақты саны үшін одан үлкен оң бүтін сан табылды, демек,
Ј
жоғарыдан шенелмеген.
3°. Барлық бүтін сандардан құрылған жиын жоғарыдаң да, төменнен де шенелмеген.
Е с к е р т у. Анықтама бойынша әрбір
x
нақты саны үшін
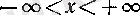 болғандықтан, кез келген сандар жиыны үшін
болғандықтан, кез келген сандар жиыны үшін
 жогары шекара, ал
жогары шекара, ал
 төменгі шекара деп айтуға болады.
төменгі шекара деп айтуға болады.
2. 3 Санды жиынның ең үлкен және ең кіші элементтері
Е caндаp жиыны берілсін. Егер сол жиынның өзінде жататын жоғарғы шекарасы бар болса, яғни
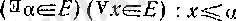 (2)
(2)
болса, онда Е жиынының ең үлкен элементі бар және ол а санына тең дейді.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz