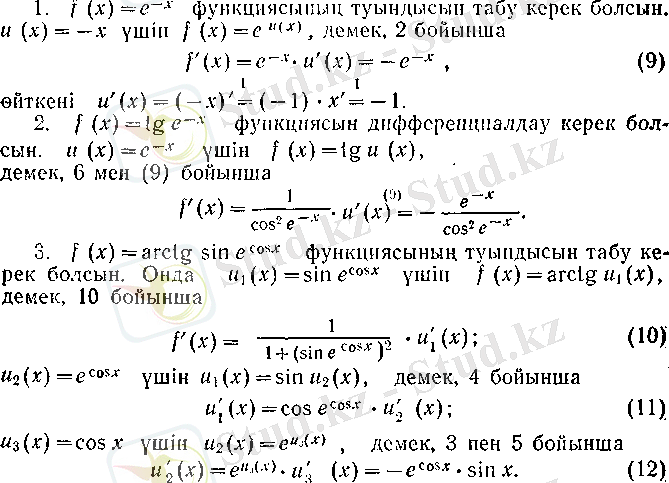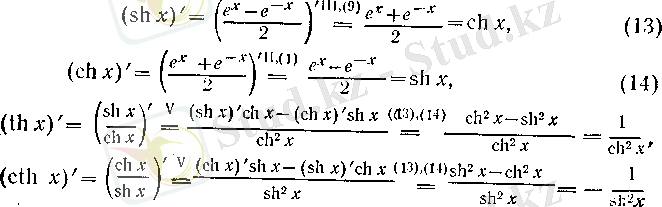Элементар функциялардың туындылары: теориясы, жоғарғы ретті туындылар және есептеу әдістері


Курстық жұмыс
Тақырыбы: Элементар функцияларды дифференциалдау
Мазмұны
Кіріспе . . .
1 Элементар функцияларды дифференциалдау . . .
1. 1 Негізгі элементар функциялардың туындылары . . .
1. 2 Элементар функциялардың туындылары туралы . . .
1. 3 Жоғарғы ретті туындылар . . .
1. 4 Негізгі элементар функцияларының жоғарғы ретті туындылары . . .
1. 5 Лейбниц формуласы . . .
2 Элементар функцияларды жіктеу, есептеу . . .
2. 1 Кейбір элементар функцияларды Маклорен формуласына жіктеу . . .
2. 2 Элементар функциялардың туындыларын есептеу . . .
2. 3 Бір айнымалыдан тәуелді функциялардың дифференциалдық есептеуі. Туынды ұғымы, дифференциалдау ережелері. Күрделі және параметрлік түрде берілген функциялардың туындысы. Кері функциялардың туындысы. Туынды кестесі . . .
Қорытынды . . .
Қолданылған әдебиеттер тізімі
3
4
4
9
14
16
17
20
20
24
27
32
33
Кіріспе
Әуелі элементар функция өзінің анықталу жиынында дифференциалданбауы да мүмкін екенін ескертейік.
Мәселен,
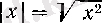 элементар функциясы барлық нақты сандар жиынында анықталған болса да,
х
о
=
0 нүктесінде туындысы (екі жақты) жоқ. Бірақ, егер
f
функциясы I аралығында элементар және дифференциалданатын болса, онда
f
' функциясы сол аралықта элементар болады. Қысқаша айтқанда, элементар функцияның туындысы да элементар функция болады.
элементар функциясы барлық нақты сандар жиынында анықталған болса да,
х
о
=
0 нүктесінде туындысы (екі жақты) жоқ. Бірақ, егер
f
функциясы I аралығында элементар және дифференциалданатын болса, онда
f
' функциясы сол аралықта элементар болады. Қысқаша айтқанда, элементар функцияның туындысы да элементар функция болады.
Бұл өте маңызды қорытынды элементар функцияның анықтамасы мен келесі екі тұжырымнан шығады. Біріншіден, негізгі элементар функциялардың туындылары да элементар функция болады (ол алдыңғы пунктте дәлелденген) . Екіншіден, егер ер функциясы дифференциалданатын f және g функцияларының қосындысы, айырымы, көбейтіндісі, бөліндісі немесе сол функциялардан құрылған күрделі функциясы болса, онда φ-дің туындысы бар болып, f , g, f ', g' функцияларына аталған амалдардың кейбіреулерінің қолданылуының нәтижесі болады (ол I-VI дифференциалдау ережелерінен байқалады) . Бұл екі тұжырымнан кез келген дифференциалданатын элементер функцияның туындысын табу үшін I-VI дифференциалдау ережелері мен негізгі элементар функциялардың туындыларының 1 -11 формулалары жеткілікті екенін көреміз. "
Курстық жұмыстың мақсаты: элементар функцияларды дифференциалдауын зерттеу.
Міндеттері:
- элементар функцияларды дифференциалдау, негізгі элементар функциялардың туындыларын қарастыру және элементар функциялардың туындылары туралы қарастыру;
- жоғарғы ретті туындыларды және негізгі элементар функцияларының жоғарғы ретті туындыларын зерттеу;
- Лейбниц формуласын қарастырып өту;
- элементар функцияларды жіктеу, есептеу, кейбір элементар функцияларды Маклорен формуласына жіктеу және элементар функциялардың туындыларын есептеу;
- бір айнымалыдан тәуелді функциялардың дифференциалдық есептеуі, туынды ұғымы, дифференциалдау ережелері, күрделі және параметрлік түрде берілген функциялардың туындысы, кері функциялардың туындысы, және туынды кестесін қарастырып өту.
1 Элементар функцияларды дифференциалдау
1. 1 Негізгі элементар функциялардың туындылары
1°. Тұрақты функцияның туындысы. Егер f тұрақты функция болса, яғни әрбір х үшін f (х) =с (с - нақты сан) теңдігі орындалса, онда f '(х о ) =0 болады.
Расында да, әрбір
х
үшін
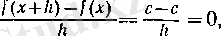
демек,
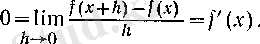
2°. Дәрежелік функцияның туындысы.
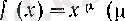 - нақты caн) болсын. Бұл функцияның анықталу жиыны µ-ға тәуелді (2 (III тарау, § 1) -пунктті қараңыз) .
х≠
0 саны сол жиынна» болсын.
- нақты caн) болсын. Бұл функцияның анықталу жиыны µ-ға тәуелді (2 (III тарау, § 1) -пунктті қараңыз) .
х≠
0 саны сол жиынна» болсын.
Онда
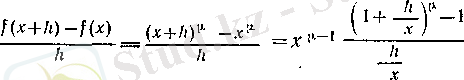
болады, демек, 2 (III т. § 8) -пункттегі дәлелденген
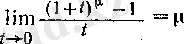 теңдігі бойынша (
теңдігі бойынша (
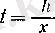 үшін пайдаланылған)
үшін пайдаланылған)
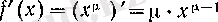 (1)
(1)
теңдігіне келеміз. (1) формуласы
 үшін
х =
0 нүктесінде де орындалады, өйткені
үшін
х =
0 нүктесінде де орындалады, өйткені
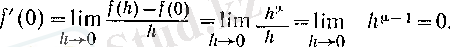
Ал
 болса, онда
f
(х) =х
болады, демек, барлық
х
нақты сандары үшін
болса, онда
f
(х) =х
болады, демек, барлық
х
нақты сандары үшін
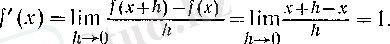
(1) -дің бірнеше дербес жағдайларын қарастырайық. Егер
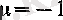 болса, онда
болса, онда
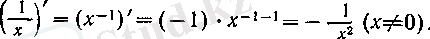
Ал
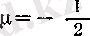 болса, онда
болса, онда
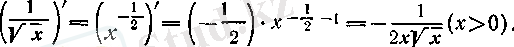
Соңында,
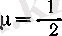 болсын. Онда
болсын. Онда
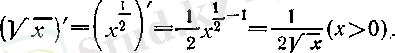
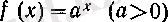
3°. Көрсеткіштік функцияның туындысы. болсын. Онда әрбір х нақты саны үшін
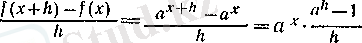
болады, демек, 2 (III т. § 8) -пункттегі дәлелденген
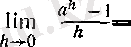
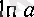 теңдігі бойынша
теңдігі бойынша
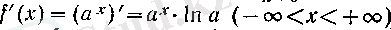 теңдігіне келеміз. Бұдан
а = е
болғанда, келесі тамаша
теңдігіне келеміз. Бұдан
а = е
болғанда, келесі тамаша
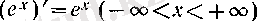
теңдігі шығады (е х функциясының туындысы өзіне тең!) .
4°. Логарифмдік функцияның туындысы.
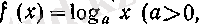
 болсын.
х
оң саны берілсін. Онда
болсын.
х
оң саны берілсін. Онда
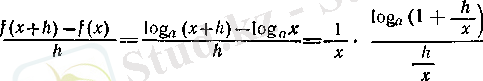
болады, демек, 4 (III тарау, § 4) -пункттегі дәлелденген
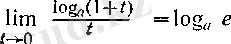 теңдігі бойынша (
теңдігі бойынша (
 үшін пайдаланылған)
үшін пайдаланылған)
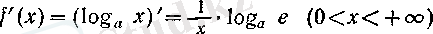 (2)
(2)
теңдігіне келеміз. Егер а = е болса, онда (2) -нің түрі өте үнемді болады:
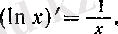
5
0
.
sin
х
пен cos
x
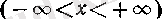 функцияларының туындылары.
функцияларының туындылары.
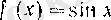 болсып. Онда
болсып. Онда
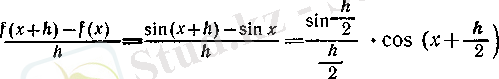
болады, демек, 3 (III т. § 3) -пункттегі дәлелденген
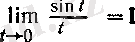 теңдігі (
теңдігі (
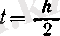 үшін пайдаланылған) және косинустың үзіліссіздігі бойынша
үшін пайдаланылған) және косинустың үзіліссіздігі бойынша
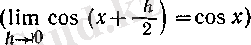
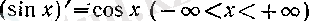 (3)
(3)
теңдігі орындалады. Дәл осылай,
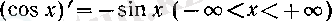 (4)
(4)
теңдігін де дәлелдеуге болады, бірақ оны біз күрделі функцияның туындысын табу ережесін қолданып дәлелдейміз:
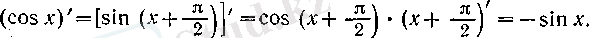
6°. tg
х
пен ctg
х
функцияларының туындылары. Әуелі
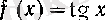 болсын. Онда
болсын. Онда
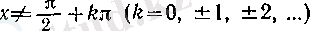 үшін бөлшекті дифференциалдаудың ережесі бойынша
үшін бөлшекті дифференциалдаудың ережесі бойынша
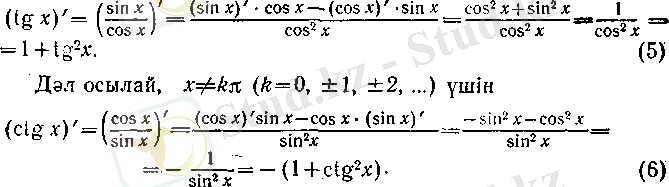
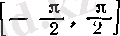 7°. arcsin
х
функциясының туындысы.
7°. arcsin
х
функциясының туындысы.
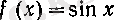 функциясын сегментінде қарастырайық. Әрине, онда
f
-тің кері функциясы болып, ол
функциясын сегментінде қарастырайық. Әрине, онда
f
-тің кері функциясы болып, ол
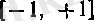 сегментінде анықталған
сегментінде анықталған
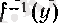 =arcsin
y
функциясы болады. Кері функцияның туындысы туралы теореманы қолданайық.
=arcsin
y
функциясы болады. Кері функцияның туындысы туралы теореманы қолданайық.
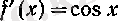 болғандықтан,
болғандықтан,
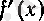 функциясы
функциясы
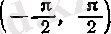 интервалында нольге айналмайды. Сондықтан, arcsin
y
функциясының ( - 1, +1) интервалында ақырлы туындысы бар болады. Енді соның мәнін табайық.
интервалында нольге айналмайды. Сондықтан, arcsin
y
функциясының ( - 1, +1) интервалында ақырлы туындысы бар болады. Енді соның мәнін табайық.
 үшін .
үшін .
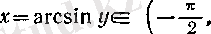
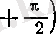 болады, демек, кері функцияның туындысын табу ережесі мен (3) теңдігі бойынша
болады, демек, кері функцияның туындысын табу ережесі мен (3) теңдігі бойынша
;
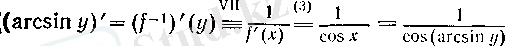 (7)
(7)
теңдігі орындалады. Жалпы
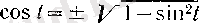 болады, ал бұл жағдайда
болады, ал бұл жағдайда
 болғандықтан, радикалдың алдында ( + ) таңбасын алу керек:
болғандықтан, радикалдың алдында ( + ) таңбасын алу керек:
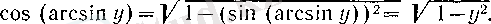
Сонымен, соңғы теңдікті ескере отырып, у -тен үйреншікті х айнымалысына көшсек, онда (7) былай жазылады
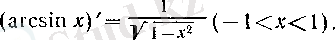
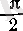 және
және
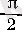 нүктелерінде
f
-тің туындысы 0-ге тең болғандықтан
нүктелерінде
f
-тің туындысы 0-ге тең болғандықтан
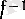 -дің оларға сәйкес -1 және 1 нүктелерінде арксинустың сәйкес оң және сол жақты туындылары бар болып, ақырсыз болады (бұл 9 (§ 1) -пункттегі 3-ескертуден шығады) .
-дің оларға сәйкес -1 және 1 нүктелерінде арксинустың сәйкес оң және сол жақты туындылары бар болып, ақырсыз болады (бұл 9 (§ 1) -пункттегі 3-ескертуден шығады) .
8°. arccos х функциясының туындысы.
f(x) =cosx
функциясын
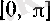 сегментінде қарастырайық. Әрине, онда
f
-тің кері функциясы бар болып, ол
сегментінде қарастырайық. Әрине, онда
f
-тің кері функциясы бар болып, ол
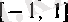 сегментінде анықталған
сегментінде анықталған
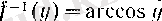 функциясы болады. 7°-де айтылғанның бәрін де arccos у үшін де қолдануға болады.
функциясы болады. 7°-де айтылғанның бәрін де arccos у үшін де қолдануға болады.
 үшін
үшін
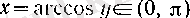 болады, демек, VII және (4) бойынша
болады, демек, VII және (4) бойынша
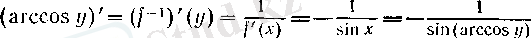 (8)
(8)
теңдігі орындалады. Жалпы
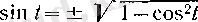 болады, ал бұл жағдайда
болады, ал бұл жағдайда
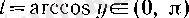 болғандықтан, радикалдың алдында ( + ) таңбасын алу керек:
болғандықтан, радикалдың алдында ( + ) таңбасын алу керек:
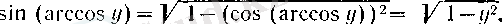
Сонымен, соңғы теңдікті ескере отырып, у-тен үйреншікті х айнымалысына көшсек, онда (8) былай жазылады.
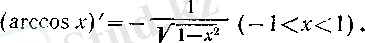
Ал - 1 және 1 нүктелерінде арккосинустың сәйкес оң және сол жақты туындылары бар болып, ақырсыз болады (мұның себептері арксинус жағдайындағыдай) .
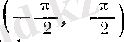 9°. arctg
х
функциясының туындысы.
f(x) =tgx
функциясын интервалында қарастырайық. Әрине, онда
f
-тің кері функциясы бар болып, ол
9°. arctg
х
функциясының туындысы.
f(x) =tgx
функциясын интервалында қарастырайық. Әрине, онда
f
-тің кері функциясы бар болып, ол
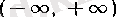 интервалында анықталған
интервалында анықталған
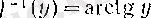 функциясы болады.
функциясы болады.
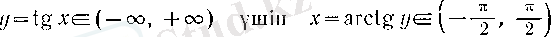
болады, демек, VII жонс (5) бойынша
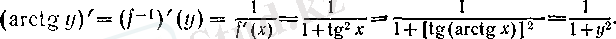
Сөйітіп, әдеттегідей у-тің орнына х -ті қойсақ, онда
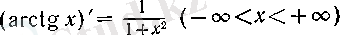
теңдігіне келеміз.
10°. arcctgx функциясының туындысы. f (х) = ctg л: функциясы (0, π) интервалында қарастырайық. Әрине, онда
f
-тің кері функциясы бар болып, ол
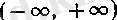 интервалында анықталған
интервалында анықталған
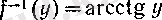 функциясы болады.
функциясы болады.
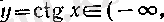 .
.
 үшін
үшін
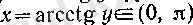 болады, демек, VII және (6)
болады, демек, VII және (6)
Бойынша
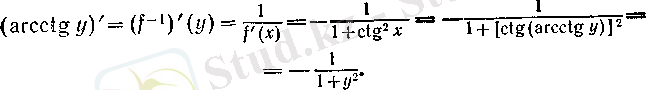
Сөйтіп, соңғы теңдікте у-ті х -ке ауыстырып жазсақ, онда
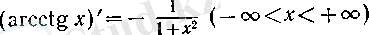
теңдігіне келеміз.
Енді
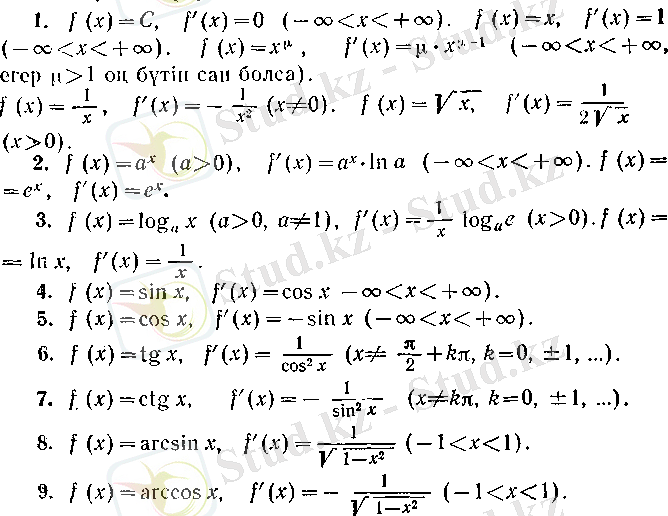
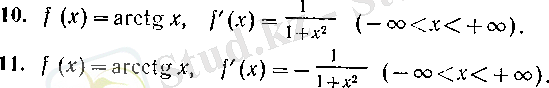
Бұдан негізгі элементар функциялардың туындылары да элементар функциялар болатыны байқалады.
1. 2 Элементар функциялардың туындылары туралы
Әуелі элементар функция өзінің анықталу жиынында дифференциалданбауы да мүмкін екенін ескертейік.
Мәселен,
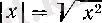 элементар функциясы барлық нақты сандар жиынында анықталған болса да,
х
о
=
0 нүктесінде туындысы (екі жақты) жоқ. Бірақ, егер
f
функциясы I аралығында элементар және дифференциалданатын болса, онда
f
' функциясы сол аралықта элементар болады. Қысқаша айтқанда, элементар функцияның туындысы да элементар функция болады.
элементар функциясы барлық нақты сандар жиынында анықталған болса да,
х
о
=
0 нүктесінде туындысы (екі жақты) жоқ. Бірақ, егер
f
функциясы I аралығында элементар және дифференциалданатын болса, онда
f
' функциясы сол аралықта элементар болады. Қысқаша айтқанда, элементар функцияның туындысы да элементар функция болады.
Бұл өте маңызды қорытынды элементар функцияның анықтамасы мен келесі екі тұжырымнан шығады. Біріншіден, негізгі элемемтар функциялардың туындылары да элементар функция болады (ол алдыңғы пунктте дәлелденген) . Екіншіден, егер ер функциясы дифференциалданатын f және g функцияларының қосындысы, айырымы, көбейтіндісі, бөліндісі немесе сол функциялардан құрылған күрделі функциясы болса, онда φ-дің туындысы бар болып, f , g, f ', g' функцияларына аталған амалдардың кейбіреулерінің қолданылуының нәтижесі болады (ол I-VI дифференциалдау ережелерінен байқалады) . Бұл екі тұжырымнан кез келген дифференциалданатын элементер функцияның туындысын табу үшін I-VI дифференциалдау ережелері мен негізгі элементар функциялардың туындыларының 1 -11 формулалары жеткілікті екенін көреміз. "
Енді сол ережелерді қолдану жөнінде кейбір нұсқаулар жасайық.
1°. Күрделі функцияның туындысын табу туралы. Әуелі негізгі элементар функциялардың туындылар таблицасын VI ереже бойынша былай жалпылап (өйткені и(х) =х үшін и'(х) = 1) жазайық:
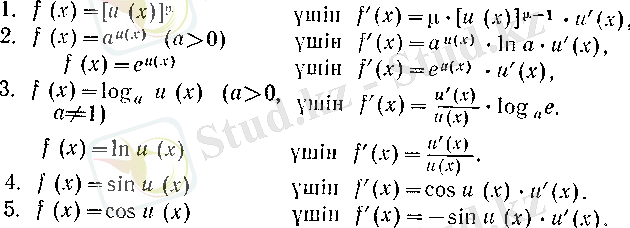
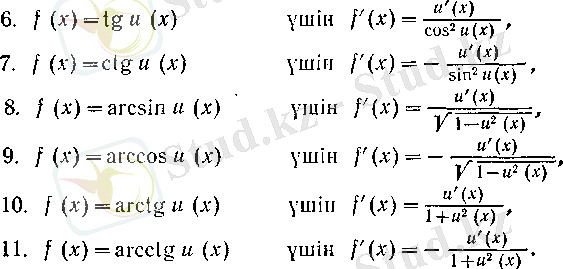
Әрине, бұндағы әрбір күрделі функция көрсетілген амалдар мағыналы болатындай шарттарды қанағаттандырады деп ұйғарамыз.
Келтірілген таблицадан мынадай қорытынды жасауға болады: егер f функциясын «сыртқы» функциясы негізгі элементар болатындай, яғни 1 -11 түрлеріндегідей, күрделі функция ретінде бейнелеу мүмкін болса, онда f табу мәселесі и (х) «ішкі» функциясының туындысын табу мәселесіне келтіріледі. Әрине, «ішкі» функцияның туындысын табу үшін осының алдында айтылғанды қайталауға болады. Бұл тәсіл «сырттан ішке» дифференциалдау деп аталады.
Айтылғанды мысалдармен толықтырайық.
Сонымен, (10), (11) және (12) бойынша
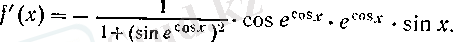
Күрделі функцияның туындысын тапқанда, оны келтірілген мысалдардағыдай құраушы функцияларға жіктеудің кажеті жоқ. Жаттығулар арқылы «сырттан ішке» қарай бірден дифференциалдауға үйренген жөн.
Енді гиперболалық функциялардың туындыларын табайық.
2°. Гиперболалық функцияларды дифференциалдау.
Егер дәлелденген формулаларды (4-7) формулаларымен салыстырсақ, онда гиперболалық пен тригопометриялық функцияларда дифференциалдау формулаларының арасында ұқсастық бар екенін көреміз.
3°. Дәрежелі-көрсеткіштік функцияның туындысын табу.
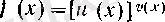 дәрежелі-көрсеткіштік функцияның туындысын табайық. Мұнда
и
және
v
функцияларының
х
нүктесінде туындысы бар болып,
и
функциясы
х
-тің белгілі бір маңайында оң деп ұйғарамыз.
дәрежелі-көрсеткіштік функцияның туындысын табайық. Мұнда
и
және
v
функцияларының
х
нүктесінде туындысы бар болып,
и
функциясы
х
-тің белгілі бір маңайында оң деп ұйғарамыз.
f -ті амықтайтын тепе-теңдіктің екі жағын да логарифмдеп, In f (x) =v (х) -In и (х) тепе-теңдігіне келеміз. Оның екі жағын да дифференциалдайық:
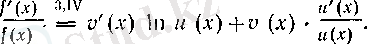
Бұдан
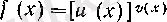 екенін ескере отырып, мақсатымыз болатын
екенін ескере отырып, мақсатымыз болатын
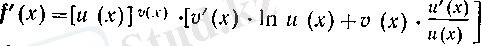 (15)
(15)
формуласына келеміз.
Мысалдар. 1.
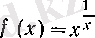 (
х
>0) болсын. Онда
и(х) = х,
(
х
>0) болсын. Онда
и(х) = х,
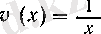 болады, демек, (15) бойынша
болады, демек, (15) бойынша
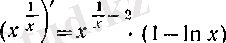 (16)
(16)
2.
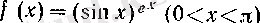 болсын. Онда
болсын. Онда
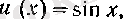
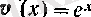 болады, демек, (15) бойынша
болады, демек, (15) бойынша
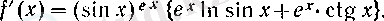
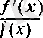 функциясын
f
(х) -тің
логарифмдік туындысы
деп атайды.
функциясын
f
(х) -тің
логарифмдік туындысы
деп атайды.
Сөйтіп, логарифмдік туынды арқылы
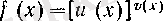 функциясының туындысы (15) формуласымен берілетінін көрдік.
функциясының туындысы (15) формуласымен берілетінін көрдік.
4°. Жалпы қорытынды.
f
функциясының
х
0
нүктесіндегі туындысын тапқанда, мына екі жағдайдың біреуі міндетті түрде орындалады. 1.
х
0
нүктесінің белгілі бір 6-маңайында
f
элементар функция болады, яғни
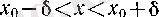 теңсіздіктерің қанағаттандыратып барлық
х
сандары үшін
теңсіздіктерің қанағаттандыратып барлық
х
сандары үшін
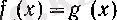 теңдігі орындалатын
g
элементар функциясы табылады. 2.
х
0
нүктесінің әрбір мадайында
f
ешқандай элементар функцияға тепе-тең болмайды.
теңдігі орындалатын
g
элементар функциясы табылады. 2.
х
0
нүктесінің әрбір мадайында
f
ешқандай элементар функцияға тепе-тең болмайды.
Бірінші жағдайда,
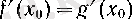 теңдігінің орындалуы айқын, ал кез келген
g
элементар функциясының туындысын табу мәеслесі жоғарыда талқыланған еді.
теңдігінің орындалуы айқын, ал кез келген
g
элементар функциясының туындысын табу мәеслесі жоғарыда талқыланған еді.
Екінші жағдайда, туындының анықтамасын тікелей пайдалануға тура келеді, яғни
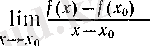 шегін табу әдісін іздеу керек.
шегін табу әдісін іздеу керек.
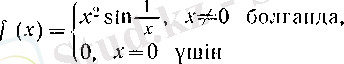
функциясының туындысын табайық.
Алдымен,
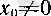 болсын. Онда
болсын. Онда
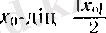 -мадайында
-мадайында
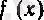 пен
пен
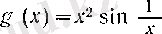 элементар функциясы тепе-тең, демек,
элементар функциясы тепе-тең, демек,
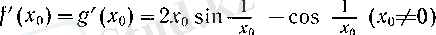
Ал
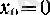 үшін, оның маңайы болатып әрбір
үшін, оның маңайы болатып әрбір
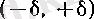 интервалында
f
функциясы бір-бірінен өзге
интервалында
f
функциясы бір-бірінен өзге
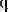 (х) ≡0
және
g (x) =х
2
(х) ≡0
және
g (x) =х
2
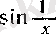 элементар функцияларын «араластыру» арқылы құрылған, демек,
элементар функцияларын «араластыру» арқылы құрылған, демек,
 элементар бола алмайды. Сондықтан, туындының анықтамасы бойынша
элементар бола алмайды. Сондықтан, туындының анықтамасы бойынша
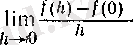 шегін табу керек.
шегін табу керек.
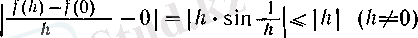
болғандықтан,
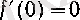 болады.
болады.
Сонымен,
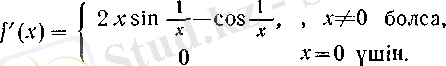
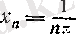 Бұл мысалдың бір қызығы, бірінші туынды әрбір нүктеде бар болса да,
Бұл мысалдың бір қызығы, бірінші туынды әрбір нүктеде бар болса да,
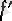 -үзіліссіз функция емес. Расында да,
-үзіліссіз функция емес. Расында да,
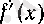 функциясы 0 нүктесінде үзілісті болады, өйткені үшін
функциясы 0 нүктесінде үзілісті болады, өйткені үшін
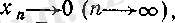 бірақ
бірақ
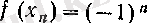 .
.
Бұл екінші түрдегі үзіліс екенін арнайы ескертейік.
1. 3 Жоғарғы ретті туындылар
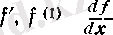
f
функцнясы I аралығында дифференциалдансын. Онда әрбір,
 санына
санына
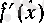 нақты санын сәйкес қоятын ереже функция болады. Ол немесе
нақты санын сәйкес қоятын ереже функция болады. Ол немесе
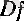 символдарымен белгіленеді. Әрине,
f
функциясының
символдарымен белгіленеді. Әрине,
f
функциясының
 нүктесінде туындысы бар болуы туралы сұрақ қоюға болады (келісім бойынша «туынды» деген сөзді «ақырлы туынды» мағынасында түсіну керек екенін еске саламыз) .
нүктесінде туындысы бар болуы туралы сұрақ қоюға болады (келісім бойынша «туынды» деген сөзді «ақырлы туынды» мағынасында түсіну керек екенін еске саламыз) .
Егер f функциясы х 0 нүктесінде дифференциалданса, яғни
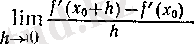
нақты мәнді шегі бар болса, онда сол шекті
f
функциясының
х
0
нүктесіндегі
екінші туындысы
деп атайды да,
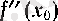 синволымен белгілейді.
синволымен белгілейді.
Егер f аралығының әрбір нүктесінде f функциясының екінші туындысы бар болса, онда f функциясы I аралығында екі рет дифференциалданады немесе екінші ретті туындысы бар дейді.
Индукция бойынша бұл анықтамалар кез келген оң бүтін п жағдайына таратылады:

f
функциясың І символымем белгілеген кейде ыңғайлы болады.
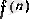 функциясы
f
функциясының
п-ші
немесе
п ретті туындысы
деп аталады да, оны белгілеу үшін
функциясы
f
функциясының
п-ші
немесе
п ретті туындысы
деп аталады да, оны белгілеу үшін
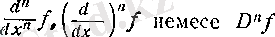
символдары да қолданылады.
f функциясының х нүктесіндегі п ретті туындысы
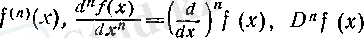
символдарының бірімен белгіленеді (оқылуы сәйкес «n-ші эф икс», «дэ эн икс бойынша дэ эн эф», «дэ эн эф икс») .
Кейде бұл символдар
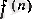 функциясының өзін де белгілеу үшін қолданылады.
функциясының өзін де белгілеу үшін қолданылады.
Келесі тұжырым өте маңызды болғандықтан, оқырманның назарын ерекше аударамыз: «
f
функциясының
х
0
нүктесінде n-ші туындысы бар» деген сөйлемді белгілі бір δ оң саны үшін
f
функциясы
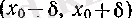 интервалында анықталып және
(п-
1) рет дифференциалданып,
интервалында анықталып және
(п-
1) рет дифференциалданып,
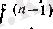 функциясынын,
х
0
нүктесінде туындысы бар болады деп түсіну керек.
функциясынын,
х
0
нүктесінде туындысы бар болады деп түсіну керек.
Расында да, бұл жоғарғы ретті туындының анықтамасының өзінен шығады: f {n) (x 0 ) нақты саны анықтама бойынша
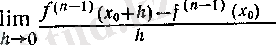
шегіне тең, ал бұл шек мағыналы болу үшін
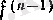 функциясы
х
0
-дің белгілі бір δ маңайында анықталуы қажет.
функциясы
х
0
-дің белгілі бір δ маңайында анықталуы қажет.
 индукция бойынша анықталғандықтан,
индукция бойынша анықталғандықтан,
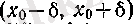
интервалында
 , . . . ,
, . . . ,
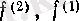 соңында
соңында
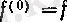 функциялары анықталған.
функциялары анықталған.
Бізге осыны көрсету керек еді.
Әрбір оң бүтін п саны үшін 0 нүктесінде n-ші туындысы бар болып, бірақ (п+ 1) -ші. туындысы болмайтын функция табылады.
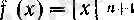 Мәселен,
п
жұп болғанда
Мәселен,
п
жұп болғанда
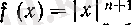 ,
п
тақ болғанда sgn
х
функциялары сондай болады. Расында да, бұл екі жағдайда да
,
п
тақ болғанда sgn
х
функциялары сондай болады. Расында да, бұл екі жағдайда да
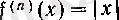 ' болады, ал
\х\
функциясы 0 нүктесінде 6 (§ 1) -пунктінде дәлелденген еді.
' болады, ал
\х\
функциясы 0 нүктесінде 6 (§ 1) -пунктінде дәлелденген еді.
Әрине, «
f
функциясының
х
0
нүктесінде n-ші оң жақты (сол жақты) туындысы бар» деген сөйлемді белгілі бір δ оң саны үшін
f
функциясы

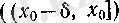 жартылай интервалында анықталып және
(п-1)
рет дифференциалданып,
жартылай интервалында анықталып және
(п-1)
рет дифференциалданып,
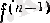 функциясының
х
0
нүктесінде оң жақты (сол жақты) туындысы бар болады деп түсіну керек.
функциясының
х
0
нүктесінде оң жақты (сол жақты) туындысы бар болады деп түсіну керек.
Мәселен,
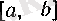 сегментінде анықталған
f
функциясының
а
нүктесінде тек қана оң жақты, ал 6 нүктесінде тек қана сол жақты жоғарғы туындылары бар болуы мүмкін.
сегментінде анықталған
f
функциясының
а
нүктесінде тек қана оң жақты, ал 6 нүктесінде тек қана сол жақты жоғарғы туындылары бар болуы мүмкін.
f
аралығында анықталып, оның әрбір нүктесінде
п
-ретті (ақырлы) туындысы бар болатын барлық функциялардан құрылған жиынды
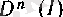 символымен белгілейді.
символымен белгілейді.
f аралығында анықталған және n-ші туындысы сол аралықта бар және үзіліссіз болатын барлық функциялардан құрылған жиын С n (І) символымен белгіленеді, яғни
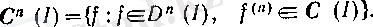
Соңында, екінші туындының механикалық мағынасын атап өтейік. Егер нүктенің қозғалысы
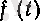 функциясымен бейнеленсе, онда
функциясымен бейнеленсе, онда
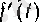 сол нүктенің қозғалысының «жылдамдығын» бейнелейді (2 (§ 1) -пунктті қараңыз), демек,
сол нүктенің қозғалысының «жылдамдығын» бейнелейді (2 (§ 1) -пунктті қараңыз), демек,
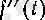 қаралып отырылған нүктенің қозғалысының «жылдамдығының жылдамдығын», яғни қозғалыстың үдеуін бейнелейді.
қаралып отырылған нүктенің қозғалысының «жылдамдығының жылдамдығын», яғни қозғалыстың үдеуін бейнелейді.
1. 4 Негізгі элементар функцияларының жоғарғы ретті туындылары
1°. Дәрежелік функцияның жоғарғы ретті туындылары.
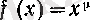 болсын. Оны бірте-бірте дифференциалдасақ, онда
болсын. Оны бірте-бірте дифференциалдасақ, онда
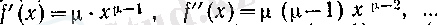 болады. Мұнан әрбір
болады. Мұнан әрбір
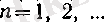 үшін
үшін
 болатынын көреміз.
болатынын көреміз.
Әрине, әрбір
ц
мен
п
үшін
х
саны
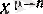 функциясының анықталу жиынынан алынады.
функциясының анықталу жиынынан алынады.
Егер
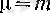 оң бүтін сан болса, онда
оң бүтін сан болса, онда
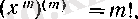 демек, тұрақты функцияның туындысы нольге тең болғандықтан, әрбір
демек, тұрақты функцияның туындысы нольге тең болғандықтан, әрбір
 үшін
үшін
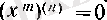 болады.
болады.
Бұдан, салдар ретінде, әрбір
п>т
үшін кез келген
т
дәрежелі
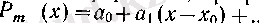
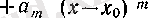 көпмүшелігінің n-ретті туындысы нольге тепе-тең болатынын көреміз.
көпмүшелігінің n-ретті туындысы нольге тепе-тең болатынын көреміз.
2°. Көрсеткіштік функциялардың жоғарғы ретті туындылары.
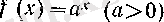 болсын. Оны бірте-бірте дифференциалдасақ, онда
болсын. Оны бірте-бірте дифференциалдасақ, онда
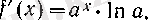
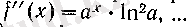 болады. Мұнан, әрбір
п
=1, 2, . . . үшін
болады. Мұнан, әрбір
п
=1, 2, . . . үшін
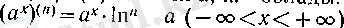 , болатынын көреміз. Егер
а - е
болса, онда
, болатынын көреміз. Егер
а - е
болса, онда
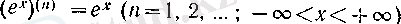
3°. Логарифмдік функцияның жоғарғы ретті туындылары. Алдымен
а ꞊
е
болсын, яғни
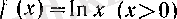 . Онда
. Онда
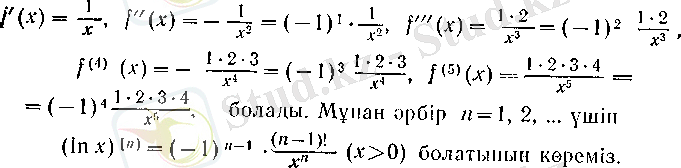
Әрине, жалпы жағдайы да осы дербес жағдайдан шығады, өнткені а > 0, а ≠ 1 үшін
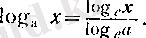
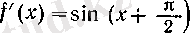 4°. Тригонометриялық функциялардың жоғарғы ретті туындылары. Алдымен
f(x) =
sin
x
болсын.
4°. Тригонометриялық функциялардың жоғарғы ретті туындылары. Алдымен
f(x) =
sin
x
болсын.
болғандықтан, әрбір дифференциалдауда аргументіне
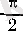 саны қосылатынын көреміз, демек,
саны қосылатынын көреміз, демек,
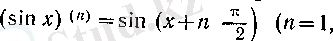 2, . . . ) . Дәл осылай,
f(x) =cos x
үшін
2, . . . ) . Дәл осылай,
f(x) =cos x
үшін
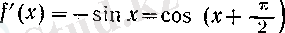 болғандықтан, әрбір
п
= 1, 2, . . . үшін
болғандықтан, әрбір
п
= 1, 2, . . . үшін
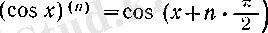 болады.
болады.
Ал тангенс, котангенс және кері тригонометриялық функциялар үшін жоғарыда қарастырылған жағдайлардағыдай қарапайым формулалар жоқ. Мәселен, математикалық индукция тәсілін қолданып
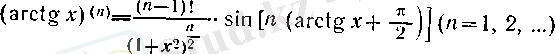
формуласын дәлелдеуге болады. Ол жаттығу ретінде оқырманның өзіне ұсынылады.
1. 5 Лейбниц формуласы
Екі функцияның қосындысы мен айырымының туындысын табу ережесі n-ретті туынды жағдайына да оңай жалпыланады, ол, әрине,
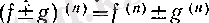 формулалары болады. Ал бөлінді мен көбейтіндіге келсек, онда бірінші амал үшін қолданылатындай формула жоқ болса, (оны
п
= 3 үшін жазып көргеннен-ақ байқауға болады), екінші амал үшін Ньютон биномының формуласына ұқсас формула бар екен. Ол
Лейбниц формуласы
деп аталады да, келесі түрдегі
формулалары болады. Ал бөлінді мен көбейтіндіге келсек, онда бірінші амал үшін қолданылатындай формула жоқ болса, (оны
п
= 3 үшін жазып көргеннен-ақ байқауға болады), екінші амал үшін Ньютон биномының формуласына ұқсас формула бар екен. Ол
Лейбниц формуласы
деп аталады да, келесі түрдегі
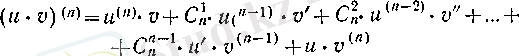 (17)
(17)
формула болады. Мұнда
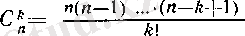 биномдық коэффициенттер.
биномдық коэффициенттер.
Лейбниц формуласын индукция бойынша дәлелдейік. п =1 үшін ол формула екі функцияның көбейтіндісінің дифференциалдану ережесіне айналады.
Енді оң бүтіп п саны үшін (17) формуласы орындалады деп ұйғарып, ( п +1) үшін де орындалатынын көрсетейік. (17) теңдігінің екі жағын да дифференциалдан, қосындыларын төменде көрсетілгендей біріктірейік:
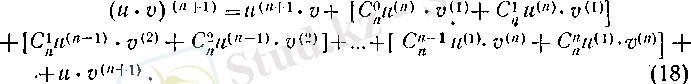
анықтамасынан
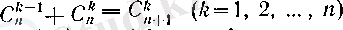 теңдігі оңай шығады. Сондықтан (18) теңдігі келесі
теңдігі оңай шығады. Сондықтан (18) теңдігі келесі
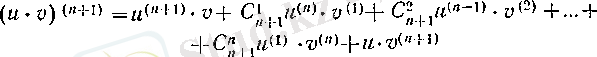
түрінде жазуға болады, демек, (17) формуласы п+1 үшін орындалатыны, сонымен бірге Лейбниц формуласы да дәлелденді.
Егер
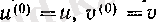 келісімімен пайдалансақ, онда Лейбниц формуласын келесі жинақты түрде жазуға болады:
келісімімен пайдалансақ, онда Лейбниц формуласын келесі жинақты түрде жазуға болады:
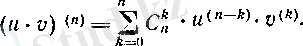
Мысалдар. 1.
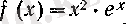 функциясының n-ші туындысын табайық. Егер
функциясының n-ші туындысын табайық. Егер
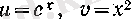 болса, онда
болса, онда
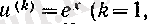 2, . . . ) ;
2, . . . ) ;
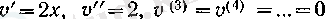 болады, демек, Лейбниц формуласы бойынша
болады, демек, Лейбниц формуласы бойынша
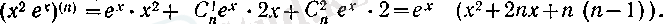
Егер көбейтіліп тұрған функциялардың біреуінің туындылары белгілі бір реттен бастап нольге тепе-тең айналып, екіншісінің туындылары оңай табылса, онда Лейбниц формуласын қолдану нәтижелі болады. Қарастырылған мысалдағы функция сондай еді.
2. Лейбниц формуласының келесі бір қызықты қолдануын келтірейік.
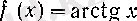 үшін
үшін
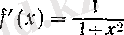 болғандықтан,
болғандықтан,
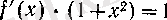 болады.
болады.
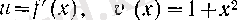 деп алсақ, онда Лейбниц формуласы бойынша
деп алсақ, онда Лейбниц формуласы бойынша
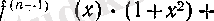
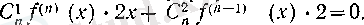 Бұдан
х = 0
болғанда арктангенстің 0 нүктесіндегі туындыларынан құрылған тізбекті анықтайтын
Бұдан
х = 0
болғанда арктангенстің 0 нүктесіндегі туындыларынан құрылған тізбекті анықтайтын
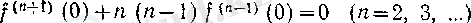 (19) :
(19) :
рекуррентті формуласына келеміз.
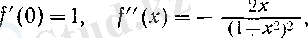
демек,
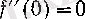 болғандықтан,
п = 2,
3, . . . үшін (19) бойынша
болғандықтан,
п = 2,
3, . . . үшін (19) бойынша
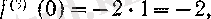
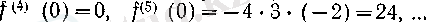 болады.
болады.
Сонымен, кейде Лейбниц формуласы арқылы n -ретті туындылардың белгілі бір нүктедегі мәндерін табуға болады.
2 Элементар функцияларды жіктеу, есептеу
2. 1 Кейбір элементар функцияларды Маклорен формуласына жіктеу
Теорема. Егер u v функциялары өздерінің бірінші ретті туындыларымен бірге
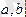 аралығында үзіліссіз болса, онда мына формула орындалады:
аралығында үзіліссіз болса, онда мына формула орындалады:
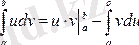 бөліктеп интегралдау
бөліктеп интегралдау
Теорема.
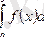 бар болсын және
бар болсын және
 функциясы мына шарттарды қанағаттандырсын:
функциясы мына шарттарды қанағаттандырсын:
1)
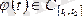 2)
2)

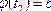
3)

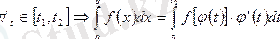
айнымалыны ауыстыру.
Мысалдар. Алдымен бөліктеп интегралдауға келтіреміз.
1.
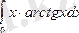
Шешуі:
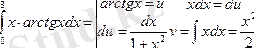
формулаға қоямыз:
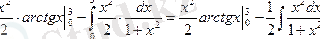
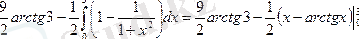
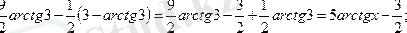
2.
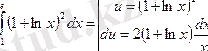
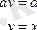
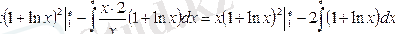
тағы да бөліктеп интегралдаймыз:
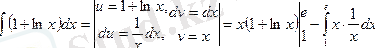
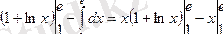 орнына қоямыз.
орнына қоямыз.
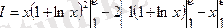
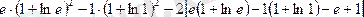
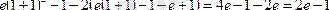
3.
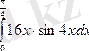
Шешуі:
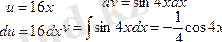
формулаға қойсақ:
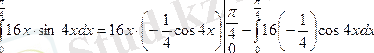
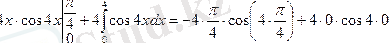
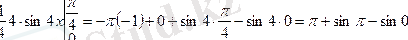

4. Келесі мысалдар айнымалыны ауыстыруға келтіріледі
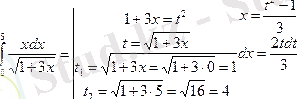
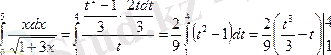
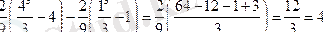
5.
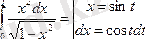
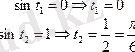
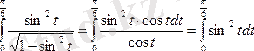
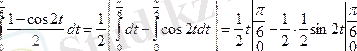
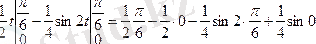

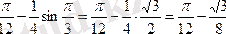
6.
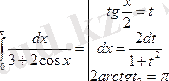
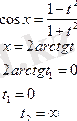
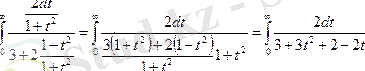
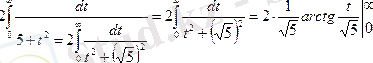
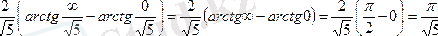
 функциясы
функциясы
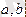 кесіндісінде үздіксіз болсын.
кесіндісінде үздіксіз болсын.
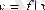 функциясы белгілі болғандықтан
функциясы белгілі болғандықтан
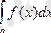 интегралының мәні осы кесіндінің шеткі нүктелері а және b сандарына тәуелді болады.
интегралының мәні осы кесіндінің шеткі нүктелері а және b сандарына тәуелді болады.
Ал енді интегралдың төменгі шегі а -ны бекітіп қойып, жоғарғы шегі b-ны айнымалы деп қарасақ, онда интегралдың мәні осы жоғарғы шектің функциясы болады. Міне осыған ерекше көңіл аудару үшін анықталған интегралды мына
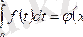 түрде жазайық.
түрде жазайық.
Бұл функцияның өте бір тамаша қасиеті бар. Оны теорема түрінде келтіріп дәлелдейік,
Теорема. Айнымалы жоғарғы шегі бойынша анықталған интегралдан алынған туындының мәні оның (интегралдың) астындағы функцияның интегралдың жоғарғы шегіндегі мәніне тең, яғни
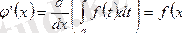
Дәлелдеуі:
 функциясының туындысын табу үшін аргумент
х
-ке
функциясының туындысын табу үшін аргумент
х
-ке
 өсімшесін береміз. Сонда
өсімшесін береміз. Сонда
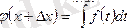
және
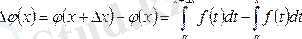
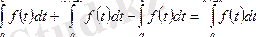
Осы теңдікке орта мән туралы теореманы, яғни қасиетті қолдансақ
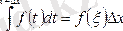
мұндағы
 және
және
 аралығында:
аралығында:
 (немесе
(немесе
 , егер
, егер
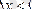 ) .
) .
Сонымен,
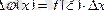
Бұдан
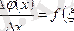 осы жерде
осы жерде
 ұмтылғандағы шекке көшсек
ұмтылғандағы шекке көшсек
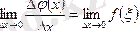
Бірақ
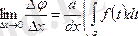
және

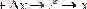
Ендеше,
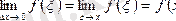
Сонымен,
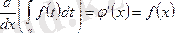
2. 2 Элементар функциялардың туындыларын есептеу
Функцияны туынды жәрдемiмен зерттеп, графигiн салу. Бұл үшiн, келесi зерттеуле/bimg
width=images/stories/lecture/mattaldau. files/image288. gifimg width=images/stories/lecture/mattaldau. files/image236. gifimages/stories/lecture/mattaldau. files/image267. gifрдi жүргiзген жөн:
1) Функцияның анықталу облысын және функция графигiнiң координат өстерiмен қиылысатын нүктелерiн табу.
2) Функцияның жұп, тақ, периодты болатындығын тексеру қажет. өйткенi, онда сәйкес оң х -тер үшiн, не ұзындығы периодқа тең аралықта зерттеу жүргiзсе болғаны.
3) Функцияны үзiлiссiздiкке зерттеп, үзiлiс нүктелерiн тауып, үзiлiс түрiн анықтау керек. Функция графигiнiң асимптоттарын табу.
4) Функцияның бiркелкi аралықтарын және экстремум нүктелерiн табу.
5) Функцияның дөңестiк (ойыстық) аралықтары және иiлу нүктелерiн табу.
6) Осы зерттеулердiң нәтижесiн пайдаланып, функция графигiн салу.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz