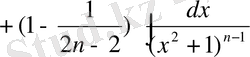Анықталмаған интеграл және интегралдаудың негізгі әдістері


Қазақстан Республикасы білім және ғылым Министрлігі
Академик Е. А. Бөкетов атындағы Қарағанды Мемлекеттік Университеті
Физика-техникалық факультеті
Радиофизика және электроника
кафедрасы
Реферат
Тақырыбы: Анықталмаған интеграл және интегралдаудың негізгі әдістері
Орындаған:
РТК-112 тобы студенті
Жансейтов Ж. Ә.
Тексерген:
Бимендина А. У.
2015
Кіріспе
Интеграл (лат. іnteger - бүтін) -
- математиканың маңызды ұғымдарының бірі. Интеграл ұғымы бір жағынан - туындысы бойынша функцияны іздеу (мысалы, қозғалған нүктенің жүріп өткен жолын өрнектейтін функцияны сол нүктенің жылдамдығы бойынша табу), екінші жағынан - аудан, көлем және доға ұзындығын өлшеу, күштің белгілі бір уақыт ішінде атқарған жұмысын табу, т. б. қажеттіліктерден пайда болды. Осыған қатысты интеграл анықталмаған интеграл және анықталған интеграл болып ажыратылады. Міне, осыларды есептеу интегралдық есептеудің міндеті болып саналады. «Интеграл» сөзін алғаш рет (1690) швейцариялық ғалым Якоб Бернулли қолданған;
- өзінің шексіз аз бөліктерінің қосындысы түрінде қарастырылатын бүтін шама.
Анықталмаған интегралды іздеу амалы немесе дифференциалдық теңдеулерді шешу.
Осыған сай дифференциалдау формулалары мен ережелеріне сүйене отырып, интегралдаудың формулалары мен ережелерін алуға болады.
1 Анықталмаған интеграл
1. 1 Анықтама
Егер
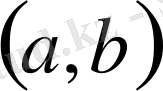 интервалының кезкелген
х
берілген нүктесінде
интервалының кезкелген
х
берілген нүктесінде
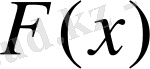 функциясы дифференциалданатын болса және оның туындысы
функциясы дифференциалданатын болса және оның туындысы
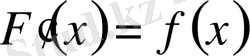 болса, онда
болса, онда
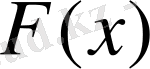 фукнциясы
фукнциясы
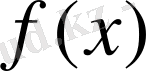 функциясының алғашқы функциясы деп аталады.
функциясының алғашқы функциясы деп аталады.
Мысал
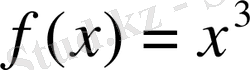 функциясының алғашқы функциясын табу керек.
функциясының алғашқы функциясын табу керек.
Шешуі
Алғашқы функцияның анықтамасы бойынша
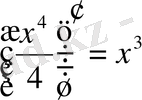 болғандықтан,
болғандықтан,
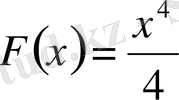 функциясы
функциясы
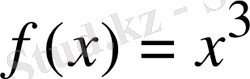 -тің алғашқы функциясы болады.
-тің алғашқы функциясы болады.
Теорема
Егер
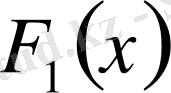 және
және
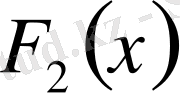
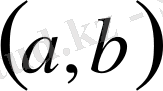 интервалында берілген
интервалында берілген
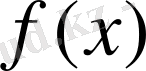 функциясының
функциясының
кезкелген алғашқы функциялары болса, онда берілген интервалда
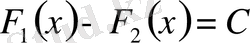 теңдігі орындалады, мұнда С- қайсы бір тұрақты. Демек, бір функцияның кезкелген алғашқы функциялары тек тұрақты шамаға ғана айрықшаланады.
теңдігі орындалады, мұнда С- қайсы бір тұрақты. Демек, бір функцияның кезкелген алғашқы функциялары тек тұрақты шамаға ғана айрықшаланады.
Алдындағы көрсетілген есепте алғашқы
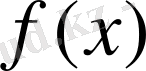 функциялары деп мына функцияларды алуға болады.
функциялары деп мына функцияларды алуға болады.
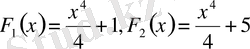 . Немесе жалпы түрде
. Немесе жалпы түрде
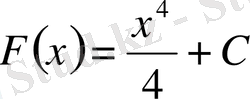 , мұнда С-
, мұнда С-
кезкелген тұрақты, өйткені
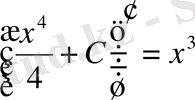 .
.
1. 2 Анықтама
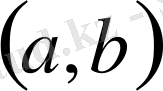 интервалында берілген
интервалында берілген
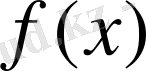 функциясының
функциясының
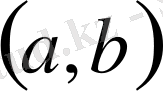 интервалында берілген барлық алғашқы функциялар жиынын анықталмаған интеграл деп атап, былай белгілейді:
интервалында берілген барлық алғашқы функциялар жиынын анықталмаған интеграл деп атап, былай белгілейді:
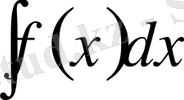
Мына белгілеуде
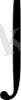 -интеграл белгісі,
-интеграл белгісі,
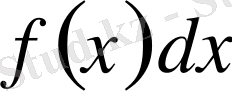 - интеграл астындағы өрнек,
- интеграл астындағы өрнек,
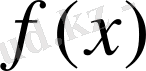 - интеграл астындағы функция,
- интеграл астындағы функция,
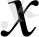 -интегралдау айнымалысы.
-интегралдау айнымалысы.
Егер
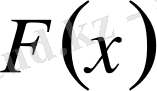 функциясы
функциясы
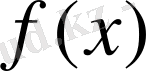 функциясының бір алғашқы функциясы болса, яғни,
функциясының бір алғашқы функциясы болса, яғни,
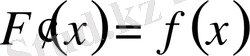 , онда
, онда
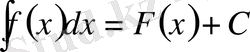 , мұнда С-кезкелген тұрақты (1)
, мұнда С-кезкелген тұрақты (1)
Интеграл астындағы
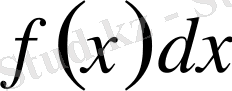 өрнек (1) теңдіктің оң жақтағы кез келген алғашқы функцияларының дифференциалы болады.
өрнек (1) теңдіктің оң жақтағы кез келген алғашқы функцияларының дифференциалы болады.
Берілген интеграл астындағы функция бойынша анықталмаған интегралды табу интегралдау амалы деп аталады. Дифференциалдау амалына қарағанда интегралдау қарама-қарсы амал. (1) Анықталмаған интегралдың геометриялық мәні:
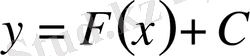 , С- параметр, қисықтар жиыны. Осы жиынға жататын қисықтар интегралдау қисықтары деп аталады. Осы жиынның кез келген қисығын Оу осінің бойымен параллель жылжытып алуға болады.
, С- параметр, қисықтар жиыны. Осы жиынға жататын қисықтар интегралдау қисықтары деп аталады. Осы жиынның кез келген қисығын Оу осінің бойымен параллель жылжытып алуға болады.
2 Анықталмаған интегралдың қасиеттері
2. 1 Анықталмаған интегралдың туындысы интеграл астындағы функцияға тең болады, яғни
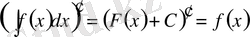
2. 2 Анықталмаған интегралдың дифференциалы интеграл астындағы өрнекке тең болады.
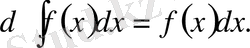
2. 3 Қайсы бір функция дифференциалының анықталмаған интегралы осы функция және кез келген С тұрақтысының қосындысына тең болады, яғни
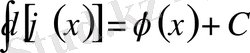
2. 4 Нөлге тең емес тұрақты көбейткішті интеграл символының алдына шығаруға болады, яғни
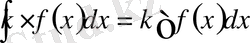
2. 5 Бірнеше функцияның алгебралық қосындысының анықталмаған интегралы әрбір функцияның анықталмаған интегралының алгебралық қосындысына тең болады, яғни
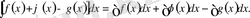
3 Негізгі интегралдар кестесі
1)
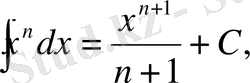 мұнда
мұнда
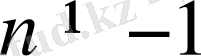
2)
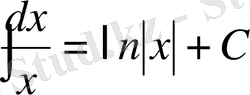
3)
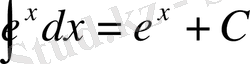
4)
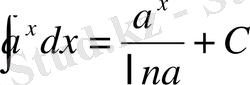
5)
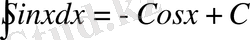
6)
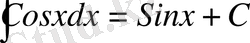
7)
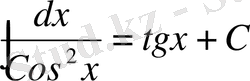
8)
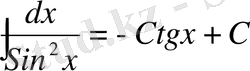
9)
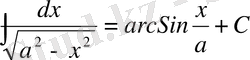
10)
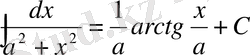
11)
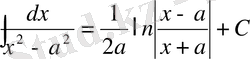
12)
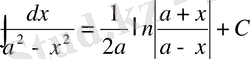
13)
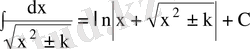
Әрбір кестелік интегралды анықталмаған интеграл анықтамасы (бойынша) және дифференциалдау амалы бойынша тексеруге болады.
4 Тікелей интегралдау
Негізгі интегралдар кестесін қолданып, анықталмаған интегралдар қасиеттерін пайдаланып интеграл астындағы өрнекті түрлендіріп интегралдағанды тікелей интегралдау деп атайды.
№1 Интегралдарды табу керек.
а)
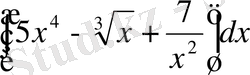 , б)
, б)
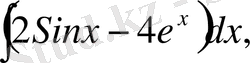
в)
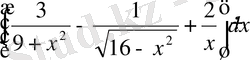
Шешуі
а) Алдымен интеграл астындағы функцияны ықшамдап, сосын анықталмаған интеграл қасиеттерін және (1) кестелік интегралды қолданып есептейміз.
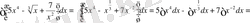
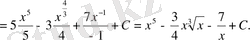
б) Анықталмаған интеграл қасиеттерін және (5), (8) кестелік интегралдарды қолданып есептейміз.
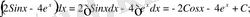
в) 4, 5 қасиеттерін және (9), (10), (2) кестелік интегралдарды қолданып, есептейміз.
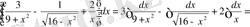

№2 Интегралдарды табу керек
а)
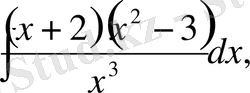 б)
б)
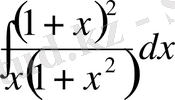 ,
,
в)
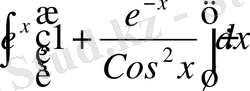 г)
г)
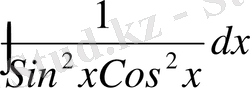
а) Алымындағы жақшаларды ашып және шыққан өрнекті
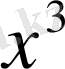 бөлеміз.
бөлеміз.
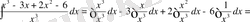
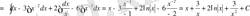
б) Алымындағы жақшаны ашып және берілген интегралды екі интегралдың қосындысы түрінде жазып, есептейміз.
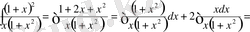
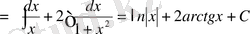
в) Жақшаны ашып, берілген интегралды екі интеграл қосындысына жіктейміз.
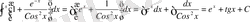
г) Берілген интегралды кестелік интегралдарға келтіру үшін алымындағы 1-дің орнына
 қойып екі интеграл қосындысына жіктейміз.
қойып екі интеграл қосындысына жіктейміз.
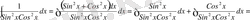
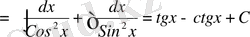
№3 Интегралдарды табу керек.
а)
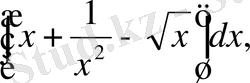 б)
б)
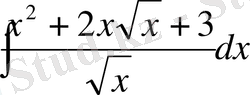 , в)
, в)
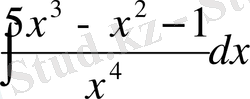 ,
,
г)
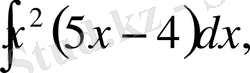 д)
д)
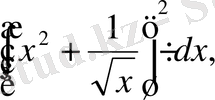 е)
е)
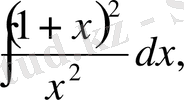
ж)
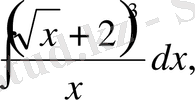 з)
з)
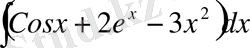
№4 а)
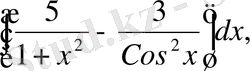 б)
б)
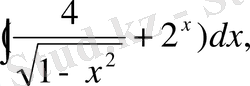 в)
в)
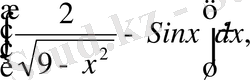
г)
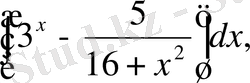 д)
д)
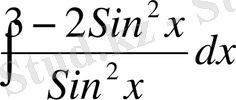 , е)
, е)
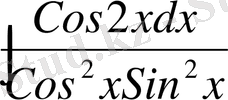
5 Айнымалыны ауыстырып интегралдау (алмастыру әдісі)
Егер
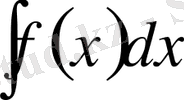 таблицалық интеграл болмаса және тікелей интегралдау әдісі бойынша табылмаса, онда көп жағдайларда жаңа айнымалыны кіргізіп берілген интегралды кестелік интегралға келтіруге болады. Алмастыру әдісінің мағынасы осы болады.
таблицалық интеграл болмаса және тікелей интегралдау әдісі бойынша табылмаса, онда көп жағдайларда жаңа айнымалыны кіргізіп берілген интегралды кестелік интегралға келтіруге болады. Алмастыру әдісінің мағынасы осы болады.
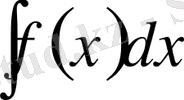 интегралды жаңа айнымалы еңгізіп, оңай интегралға келтіруге болады. Интеграл астындағы өрнектегі айнымалыны ауыстырайық, яғни
интегралды жаңа айнымалы еңгізіп, оңай интегралға келтіруге болады. Интеграл астындағы өрнектегі айнымалыны ауыстырайық, яғни
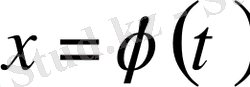 деп алсақ мұндағы
деп алсақ мұндағы
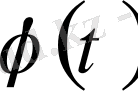 кері функциясы бар үздіксіз функцияның үздіксіз туындысы. Онда
кері функциясы бар үздіксіз функцияның үздіксіз туындысы. Онда
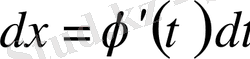 және мына теңдікті аламыз.
және мына теңдікті аламыз.
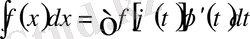
Осы алмастыруды қолданып интегралды есептегеннен кейін, оны алғашқы берілуіндегі
х
айнымалысына қайтадан оралуымыз керек. Кейбір жағдайда
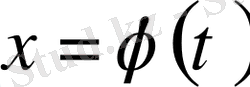 алмастырудың орнына
алмастырудың орнына
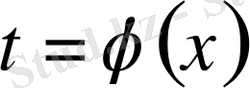 алмастыруды қолдану керек, яғни жаңа
t
айнымалыны
x
-ке тәуелді функция деп қарастырамыз.
алмастыруды қолдану керек, яғни жаңа
t
айнымалыны
x
-ке тәуелді функция деп қарастырамыз.
№5
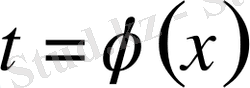 алмастыруды қолданып интегралды табу керек.
алмастыруды қолданып интегралды табу керек.
а)
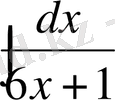 , б)
, б)
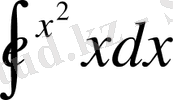 , в)
, в)
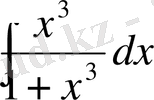 ,
,
г)
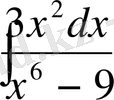 , д)
, д)
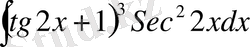
а) Егер
t=6x+1
алмастыруды қолдансақ, онда
dt=6dx
және
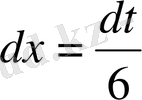 .
.
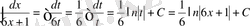
б) Берілген интегралды кестелік интегралға келтіру үшін
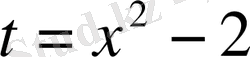 деп алып, онда
деп алып, онда
 және
және
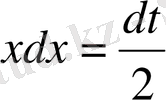 . (2) формуланы қолданып есептейміз.
. (2) формуланы қолданып есептейміз.
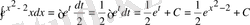
в) Берілген интегралды кестелік интегралға келтіру үшін
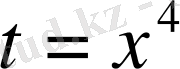 , онда
, онда
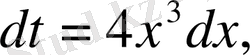
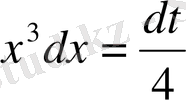 . Ендеше,
. Ендеше,
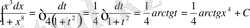
г)
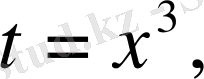 онда
онда
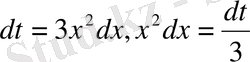 .
.
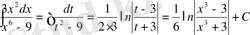
д)
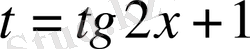 , онда
, онда
 және
және
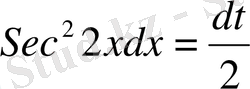 .
.
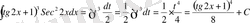 ;
;
№6 Интегралдарды табу керек.
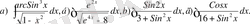
а
)
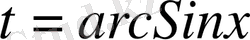 деп аламыз, онда
деп аламыз, онда
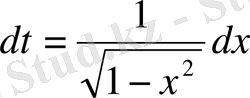 . Ендеше,
. Ендеше,
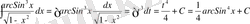
Кейбір кезде, егер алдын ала, қандай алмастыру интегралды кестелік интегралға келтіретінін көрініп тұрса, онда жаңа айнымалыны кіргізу керек емес. Мысалға
а)
пунктін алсақ, онда
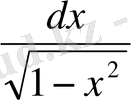 arcSinx
- тің дифференциалы екені көрініп тұр. Сондықтан, шешімін былай жазуға болады:
arcSinx
- тің дифференциалы екені көрініп тұр. Сондықтан, шешімін былай жазуға болады:
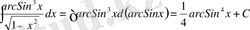
б
)
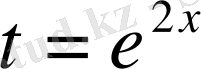 деп аламыз, онда
деп аламыз, онда
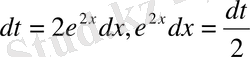 . Ендеше,
. Ендеше,
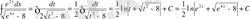
в
)
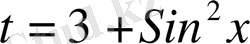 деп аламыз, онда
деп аламыз, онда
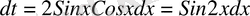 . Ендеше,
. Ендеше,
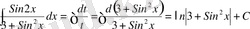 ;
;
Осы есепті шығарғанда жаңа айнымалыны кіргізбей ақ былай интегралдауға болады.
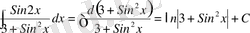
г)
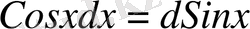 болғандықтан, берілген интеграл кестелік интегралға келтірілді.
болғандықтан, берілген интеграл кестелік интегралға келтірілді.
Алмастыру әдісін қолданып, келесі интегралдарды табу керек.
№7
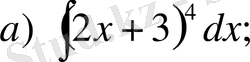
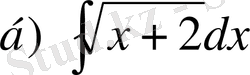 ,
,
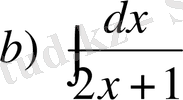 ,
,
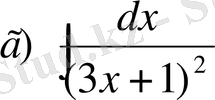 ,
,
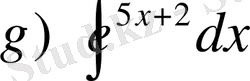 ,
,
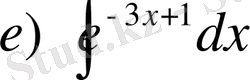
№8
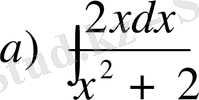 ,
,
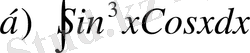 ,
,
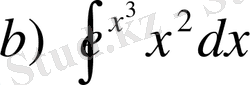 ,
,
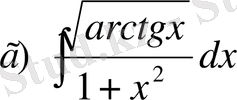 ,
,
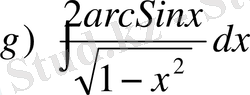 ,
,
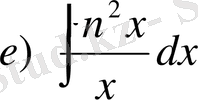
№9
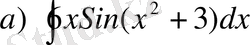 ,
,
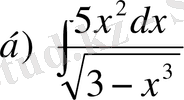 ,
,
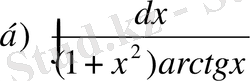 ,
,
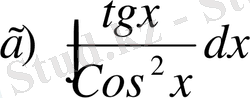 ,
,
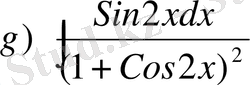 ,
,
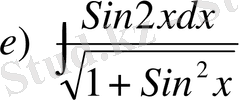
№10
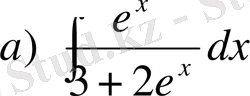 ,
,
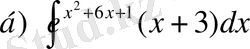 ,
,
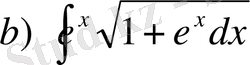 ,
,
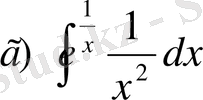 ,
,
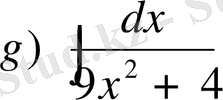 ,
,
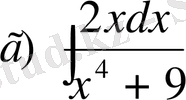
№11
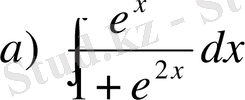 ,
,
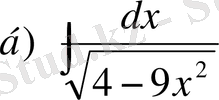 ,
,
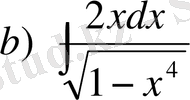 ,
,
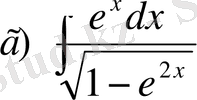 ,
,
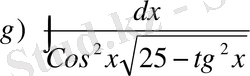 ,
,
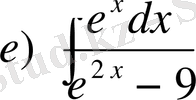
№12
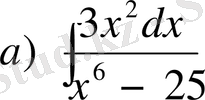 ,
,
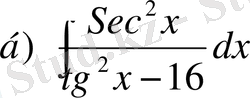 ,
,
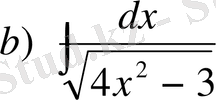 ,
,
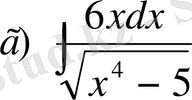 ,
,
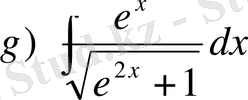 ,
,
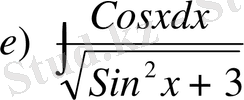
6 Бөліктеп интегралдау әдісі
Егер
u(x)
және
v(x)
қайсы бір аралықта үздіксіз, аралықтың әрбір ішкі нүктесінде дифференциалданатын функциялар болып және осы аралықта
 бар болса, онда
бар болса, онда
 бар болады,
бар болады,
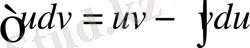 (3)
(3)
Егер
 берілген
берілген
 интегралға қарағанда әлдеқайда қарапайым интеграл болса, (3) формуланы бөліктеп интегралдау формуласы деп атайды. Осы формуланы қолдануға болады, .
интегралға қарағанда әлдеқайда қарапайым интеграл болса, (3) формуланы бөліктеп интегралдау формуласы деп атайды. Осы формуланы қолдануға болады, .
№13 (3) формуланы қолданып, мына интегралдарды табу керек:
 . 3,
. 3,
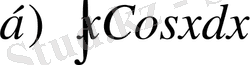 . 3
. 3
Шешуі
(3) формуланы қолданамыз
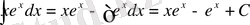
б)
u=x
және
dv=Cosxdx
деп аламыз. Онда
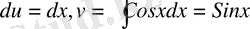
Ендеше,
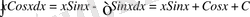
(3) формуланы қолданғанда, u және dv дұрыс таңдап алу керек. Интеграл астындағы өрнекті u және dv көбейткіштерге бөліктейтін жалпы ереже жоқ. Бірақ кейбір дербес нұсқауларды қолдануға болады.
Нұсқау 1
Егер интеграл астындағы өрнек көпмүшелік пен көрсеткіштік
функцияның, не болмаса көпмүшелік пен тригонометриялық функцияның көбейтіндісі болса, онда u деп көпмүшелікті белгілейміз.
Нұсқау 2
Егер интеграл астындағы өрнек көпмүшелік пен логаримфдік
функция, не болмаса көпмүшелік пен кері тригонометриялық функцияның көбейтіндісі болса, онда u деп логарифдік функцияны, не болмаса кері тригонометриялық функцияны алу керек.
№14 Интегралдарды табу керек.
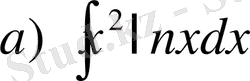 ,
,
 ,
,
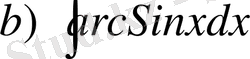
Шешуі
 Нұсқау 2 -ні қолданып,
Нұсқау 2 -ні қолданып,
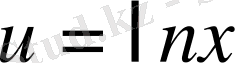 және
және
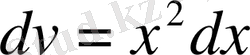 деп белгілейміз.
деп белгілейміз.
Онда
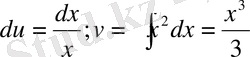 . Бөлшектеп интегралдау әдісінің формуласын қолданып, интегралды мына түрге келтіреміз.
. Бөлшектеп интегралдау әдісінің формуласын қолданып, интегралды мына түрге келтіреміз.
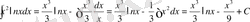
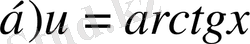 және
dv=2xdx,
онда
және
dv=2xdx,
онда
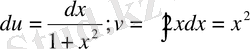 . Бөлшектеп
. Бөлшектеп
интегралдау әдісінің формуласын қолданып,

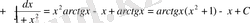
а) u=arcSinx
және
dv=dx
болсын, онда
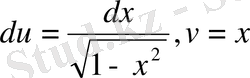 Демек,
Демек,
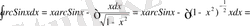
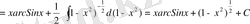
№15 Бөліктеп интегралдау формуласын қолданып, интегралды табу қажет.
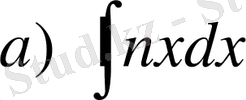 ,
,
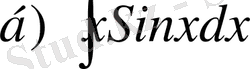 ,
,
 ,
,
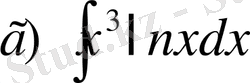 ,
,
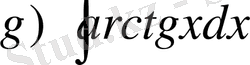 ,
,
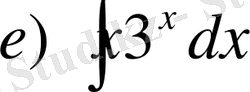 ,
,
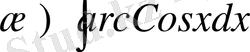 ,
,
 ,
,
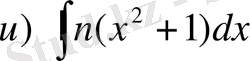
№16 Бөліктеп интегралдау формуласын 2 рет қолданып, берілген интегралдарды есептеу керек:
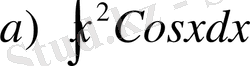 ,
,
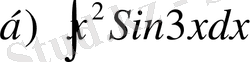 ,
,
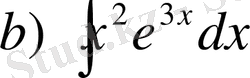
Нұсқау 3
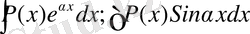 және
және
 , мұнда Р(х) көпмүшелік, түрдегі интегралдарды табу үшін көпмүшелік дәрежесі қанша болса, сонша рет бөліктеп интегралдау формуласын қолдану қажет. Сонымен қатар, көбейткіш u- деп әр кезде дәрежелік функцияны белгілейді.
, мұнда Р(х) көпмүшелік, түрдегі интегралдарды табу үшін көпмүшелік дәрежесі қанша болса, сонша рет бөліктеп интегралдау формуласын қолдану қажет. Сонымен қатар, көбейткіш u- деп әр кезде дәрежелік функцияны белгілейді.
Кейбір жағдайларда бөліктеп интегралдау формуласын бірнеше рет қолданғанда ізделінетін интегралға қатысты теңдеу шығады. Мұндай интегралдарға мына интегралдар жатады.
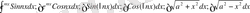
№17
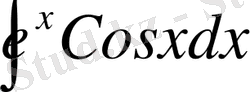 интегралды табу керек.
интегралды табу керек.
Шешуі
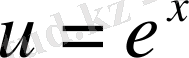 және
және
 , онда
, онда
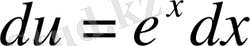 және
және
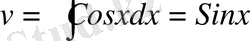 . Осыдан
. Осыдан
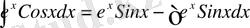 (*)
(*)
(*) алынған интегралдың оң жағын бөліктеп интегралдау әдісімен интегралдаймыз.
Айталық
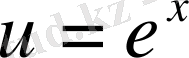 және
және
 , онда
, онда
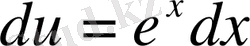 ,
,
 және
және
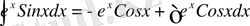 (**)
(**)
(**) - ны (*) -ға қойсақ ізделінді интегралға қатысты формуланы аламыз.
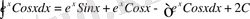 , осыдан
, осыдан
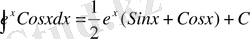
№18
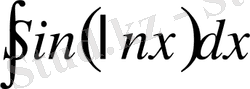 интегралды тап.
интегралды тап.
Шешуі
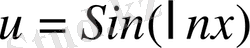 және
dv=dx
онда
және
dv=dx
онда
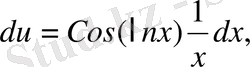 v=x
және
v=x
және
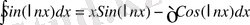 .
.
Бөліктеп интегралдау формуласын қолданып
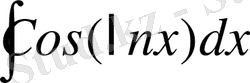 табамыз.
табамыз.
Айталық
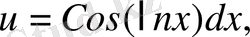 және
dv=dx
деп алсақ
және
dv=dx
деп алсақ
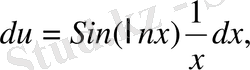
v=x
және
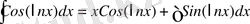 . Сонымен
. Сонымен
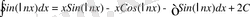 , бұдан
, бұдан
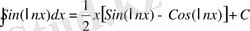
№19 Интегралды тап
Шешуі
Иррационалдықты бөліміне және берілген интегралды екі интегралдың қосындысы түріне келтіреміз.
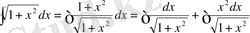
Бірінші интеграл (13) кестелік интеграл болып табылады, ал екінші интегралды бөліктеп интегралдаймыз.
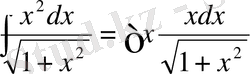 .
.
 десек
десек
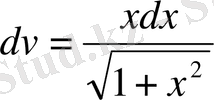 , онда
, онда
 , және
, және
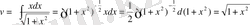
Сонымен,
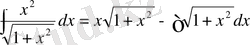
және
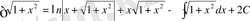 осыдан
осыдан
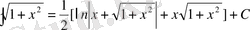
№20 Интегралдарды есептеңдер
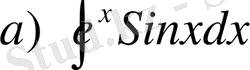 ,
,
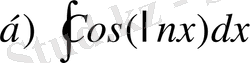 ,
,
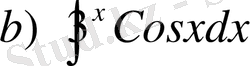
№21 Интегралға рекурренттік формуласын еңгіземіз.
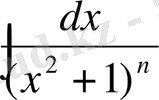
Шешуі
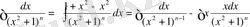 (*)
(*)
(*) алынған интегралды бөліктеп интегралдау формуласын пайдаланып есептейміз.
 және
және
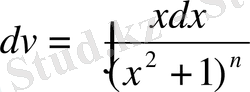 десек, онда
десек, онда
 ,
,
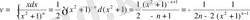
Сонымен,

немесе
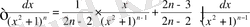 (4)
(4)
(4) формула рекуренттік формула деп аталады. Ол мына
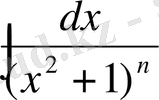 интегралды
интегралды
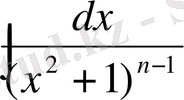 арқылы өрнектеуге мүмкіншілік береді, яғни бөлімінің дәрежесін бір дәрежеге төмендетеді. Сонымен (4) формуланы
арқылы өрнектеуге мүмкіншілік береді, яғни бөлімінің дәрежесін бір дәрежеге төмендетеді. Сонымен (4) формуланы
 рет қолданса берілген интеграл кестелік түрге келеді.
рет қолданса берілген интеграл кестелік түрге келеді.
7
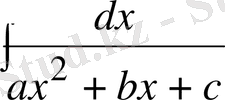 және
және
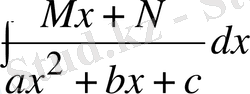 түрдегі интегралдар
түрдегі интегралдар
Берілген
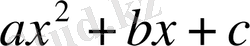 квадраттық үшмүше
квадраттық үшмүше
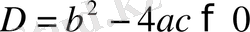 болған жағдайда нақты және әр түрлі түбірлері болады; D=0 болған жағдайда еселі түбірлері болады; D<0 комплекс түбірлері болады. Бірінші жағдайда квадраттық үшмүшені екі квадраттың айырмасы ретінде алуға болады, екінші жағдайда үшмүше толық квадрат болып табылады, ал үшінші жағдайда ол екі квадраттың қосындысы ретінде көрсетіледі. Сонымен, егер D>0 болса
болған жағдайда нақты және әр түрлі түбірлері болады; D=0 болған жағдайда еселі түбірлері болады; D<0 комплекс түбірлері болады. Бірінші жағдайда квадраттық үшмүшені екі квадраттың айырмасы ретінде алуға болады, екінші жағдайда үшмүше толық квадрат болып табылады, ал үшінші жағдайда ол екі квадраттың қосындысы ретінде көрсетіледі. Сонымен, егер D>0 болса
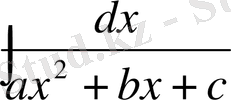 (А) түрдегі интеграл (11) кестелік интегралға келеді, егер D<0 болса, (10) кестелік интегралға келеді, егер D=0 болса, (1) кестелік интегралға келеді.
(А) түрдегі интеграл (11) кестелік интегралға келеді, егер D<0 болса, (10) кестелік интегралға келеді, егер D=0 болса, (1) кестелік интегралға келеді.
Сонымен (А) түрдегі интегралдарды табу үшін квадраттық үшмүшелікті түрлендіріп (толық квадратты бөліп алу) және (10), (11), (1) кестелік интегралдарды қолдану керек.
№22 Интегралдарды табыңдар
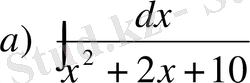 ,
,
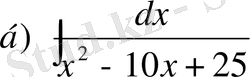 ,
,
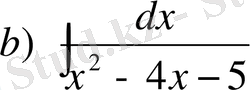
Шешуі
а)
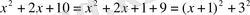
(10) формуланы қолданып
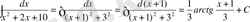
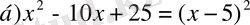 , сонымен
, сонымен
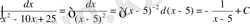
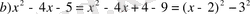
(11) формуланы пайдаланып,
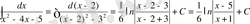
№23 Интегралдарды есептеңдер
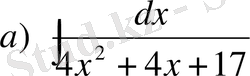 ,
,
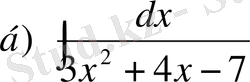
Шешуі
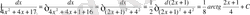
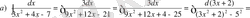
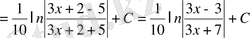
№24 Интегралдарды есептеңдер
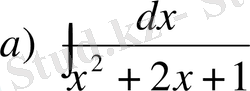 ,
,
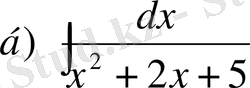
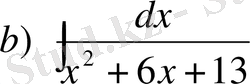 ,
,
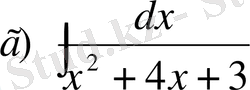
№25 Интегралдарды есепте
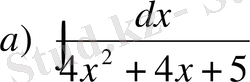 ,
,
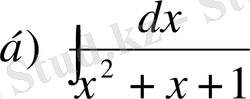
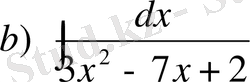 ,
,
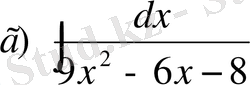
Мынадай түрдегі интегралды қарастырайық
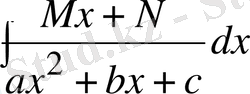 (В) Егер
(В) Егер
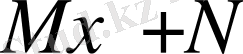 өрнек
өрнек
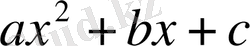 үшмүшеліктің туындысы болатын болса, онда (В) интеграл (2) кестелік формуламен алынады.
үшмүшеліктің туындысы болатын болса, онда (В) интеграл (2) кестелік формуламен алынады.
Егер
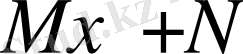 өрнек бөлімінің туындысы болмаса, онда өрнекті бөлімінің туындысы болатындай етіп түрлендіру керек. Содан кейін (В) интегралын екі интегралдың қосындысы ретінде жазамыз, оның біріншісі тікелей алынады ал, екіншісі (А) интеграл түріне келеді.
өрнек бөлімінің туындысы болмаса, онда өрнекті бөлімінің туындысы болатындай етіп түрлендіру керек. Содан кейін (В) интегралын екі интегралдың қосындысы ретінде жазамыз, оның біріншісі тікелей алынады ал, екіншісі (А) интеграл түріне келеді.
№26 Интегралды табу керек.
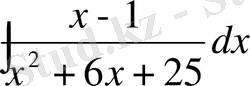
Шешуі
Бөлімінің туындысы
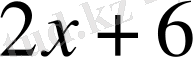 . Алымын бөлімінің туындысы бола алатындай етіп түрлендіреміз де, оны екі интегралға бөлеміз.
. Алымын бөлімінің туындысы бола алатындай етіп түрлендіреміз де, оны екі интегралға бөлеміз.
Конец формы
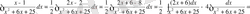

№27 Интегралды тап
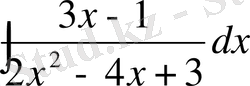
Шешуі
Бөлімінің туындысы
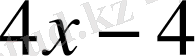 . Түрлендіру жасап, мынаны аламыз.
. Түрлендіру жасап, мынаны аламыз.
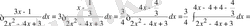
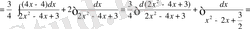
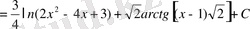
№28 Интегралдарды табыңдар
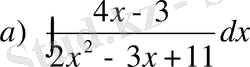 ,
,
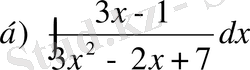
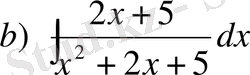 ,
,
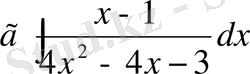
8 Интегралдардың тағы бір түрлері
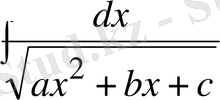 және
және
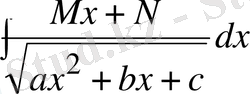
Алдымен мына түрін қарастырайық
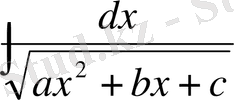 (С)
(С)
(С) интегралы егер
 болған жағдайда, (13) кестелік интегралға келеді және егер
болған жағдайда, (13) кестелік интегралға келеді және егер
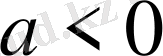 болса, онда (9) кестелік интегралға келеді.
болса, онда (9) кестелік интегралға келеді.
№29
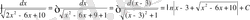
№30
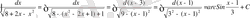
№31
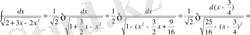
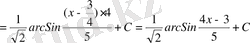
№32 Интегралдарды табыңдар
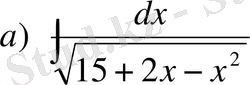
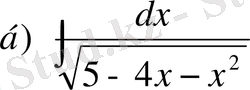
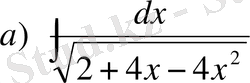
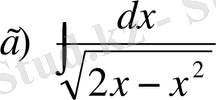
Енді мына түрдегі интегралды қарастырайық
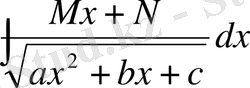 (D)
(D)
Егер
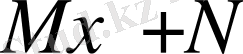 өрнек
өрнек
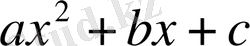 үшмүшеліктің туындысы болатын болса, онда (D) интеграл (1) кестелік формуламен тікелей алынады. Егер
үшмүшеліктің туындысы болатын болса, онда (D) интеграл (1) кестелік формуламен тікелей алынады. Егер
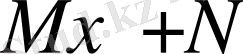 өрнек бөлімінің туындысы болмаса, онда бөліміндегі өрнектің туындысы бөлініп алынатындай етіп түрлендіру керек. Содан кейін (D) интегралды екі интегралдың қосындысы ретінде жазамыз, оның біріншісі тікелей алынатын ал, екіншісі (С) интеграл түріне келеді.
өрнек бөлімінің туындысы болмаса, онда бөліміндегі өрнектің туындысы бөлініп алынатындай етіп түрлендіру керек. Содан кейін (D) интегралды екі интегралдың қосындысы ретінде жазамыз, оның біріншісі тікелей алынатын ал, екіншісі (С) интеграл түріне келеді.
№33
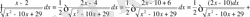
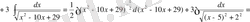
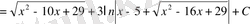
№34
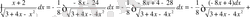
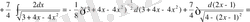
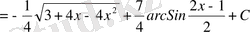
№35 Интегралдарды есептеңдер
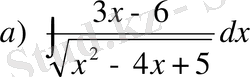 ;
;
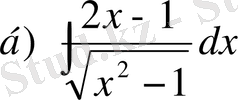
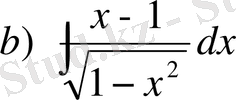 ;
;
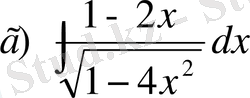
9 Рационал бөлшектерді қарапайым бөлшектерге жіктеу
Айталық
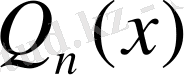
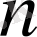 -дәрежелі нақты коэффициентті көпмүшелік болсын.
-дәрежелі нақты коэффициентті көпмүшелік болсын.
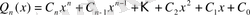 (1)
(1)
(1) көпмүшелігі
 түрдегі сызықтық және
түрдегі сызықтық және
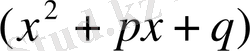 түрдегі квадраттық көпмүшелікке ғана жіктеле алатыны белгілі, мұндағы
түрдегі квадраттық көпмүшелікке ғана жіктеле алатыны белгілі, мұндағы
 -көпмүшеліктің нақты түбірі, ал
-көпмүшеліктің нақты түбірі, ал
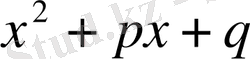 квадраттық үшмүшеліктің нақты түбірі жоқ, басқаша айтсақ
квадраттық үшмүшеліктің нақты түбірі жоқ, басқаша айтсақ
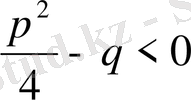 .
.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz