Биология мамандықтарында математиканы оқыту әдістері мен математикалық модельдеу


А. Ясауи университетініњ хабаршысы, №1, 2011
Б. Ж. АЛИХАНОВА
А. Ясауи атындағы ХҚТУ-нің оқытушысы
Биология мамандықтарында математиканы оқытудың
кейбір әдістері
В настоящей работе рассматриваются некоторые методы обучения математики в биологических специальностях.
In this paper we consider some methods of teaching mathematics in biology specialty.
Еліміздегі қазіргі кездегі өзгерістер, экономиканы дамытудағы стратегиялық жаңа бағдар, жедел ақпараттану мен әлеуметтік даму қарқыны білім беру жүйесіне, кәсіби мамандар даярлауға зор талап қояды және өз ісін жетік білетін және кәсіби біліктілігі биік мамандарды қажет етеді.
«Қазақстан Республикасының 2015 жылға дейінгі білім беруді дамыту тұжырымдамасында»: « . . . мамандар даярлау жүйесінде білім берудің жоғары сапасын қамтамасыз етуде жоғары білімді дамытудың негізгі үрдісі мамандар даярлау сапасын арттыру, . . . білім беру және ақпараттық технологияны жетілдіру болып табылады».
Қоғам дамуының қазіргі кезеңі адам қызметінің басым көпшілік түрлерін математикаландырумен ерекшеленеді. Математика ғылым мен техниканың қазіргі кезеңдегі көптеген салаларының дамуының теориялық негізі болып отыр. Компьютерлік технологияның дамуы математиканың тиянақты есептерді шешуде ауқымын кеңейтуге негіз болды. Соған байланысты математиктердің қызмет аясы кеңейіп, математикалық әдістердің практикалық сұранысы артты. Сондықтан математиканы оқыту сапасын жақсартудың өзектілігі айқын көрініс тауып отыр.
Жаратылыстану бағытындағы пәндерде математиканың рөлі әр түрлі және уақытқа байланысты өзгеріп отырады. Химия, физика пәндеріне қарағанда математиканы биологияға қолдану біршама кештеу енгізілгеніне қарамастан құбылыстарды сапалы талдау негізінде (табиғи сұрыптау, Дарвин ілімі, т. б. математиканың көмегінсіз сапалы болжамдар жасалынды) биология ұзақ дамыды. Биологияға математиканы қолдануға XVII ғасырдың соңымен XVIII ғасырдың басында талпыныстар жасалды. Жануарлар қозғалысының математикалық есебін Д. А. Борелли (1608-1679 ж. ж. ), ара ұясының құрылысының математикалық заңдылығын ашуға Р. А. Ремюр (1683-1757ж. ж. ) ашуға талпынғанымен тек XIX ғасырда ғана математикалық әдістерді пайдаланып табиғаттағы құбылыстарға сандық талдау жасау қажеттілігі пайда болды. Антропометрия әдістері мен әлеуметтік статистиканы ықтималдықтардың математикалық теориясымен ұштастыру арқылы А. Кетле (1796-1874 ж. ж. ) өзінің «Адам және оның қабілеттерінің жетілуі туралы, немесе әлеуметтік физика» деген кітабында (1869 ж. ) адамның физикалық ерекшеліктері мен мінез-құлқы ықтималдықтың үлестіру заңына бағынатындығын дәлелдеді. Сондай-ақ, ол кейін кездейсоқтықты және олардың табиғаты қайталанып отыратындықтарын бақылау арқылы белгілі заңдылықтарға сүйеніп, оларды зерттеуге және нақты математикалық тәсілдерін беруге болатындығын көрсетті. А. Кетленің статистикалық әдістерін алғаш рет тұқым қуалаушылық және ағзаның өзгергіштігі проблемаларын шешуде қолданып Ф. Гальтон (1822-1911ж. ж. ) регрессиялық және корреляциялық талдау әдістерін тапты. Биометрияның негізін салды. ХIХ соңымен XX ғасырдың басында биологиялық зерттеу жұмыстарына математикалық әдістер қолдану қарқынды түрде қолға алынды. К. Пирсон (1857-1936 ж. ж. ), биометриядағы математикалық аппаратты жетілдірді, Р. Фишер (1890-1962 ж. ж. ) дисперсиялық талдау әдістерін жасап шығарды.
В. Вольтерра (1860-1940) интегралдық теңдеулер және функционалдық талдау саласындағы еңбектері үшін әлемге әйгілі ғалым. Оны таза ғылыми математикадан басқа математикалық әдістерді биологияға, физикаға, әлеуметтік ғылымдарға қолдану қызықтырды. 1931 жылы В. Волтерра Парижде дифференциалдық және интегралдық теңдеулер көмегімен бірнеше биологиялық түрлердің біреуінің екіншісіне қарағанда жыртқыш болып келген жағдайда бірге өмір сүруі мүмкіндігінің моделін құрды. Оны жан-жақты зерттеуін ұсынып, биологиялық мәселелерді математика арқылы шешу үлгісін көрсеткендігі оның монографиялық еңбектерінен белгілі.
Қазіргі таңда биологиядағы математикалық әдістердің рөлі артқандықтан:
- Кез-келген биологиялық тұжырым физиканың және химияның заңдарына негізделгендіктен оған математикалық аппарат қолдану қажеттілігі белгілі;
- Жаңа эксперименттік ақпараттың санының көптігінен оны математикалық аппаратсыз жүйелеу мүмкін емес.
- Математиканың көмегінсіз пайда болған биологиялық заңдылықтар мен жағдайларға заманауи математиканы қолдану оларға өте дәл және маңызды пішін беріп, бұрын белгісіз жағдайларды анықтауға болады.
Нақты биологиялық есептерді шешуде математикалық әдістердің рөлі артқан сайын биология мамандығын таңдаған студенттерге математиканы қалай оқыту керек және нені оқыту керек деген сұрақтың қойылуы заңды және математиканы оқыту кезінде дәріс материалын таңдау, студенттің мектеп бағдарламасындағы алған математикалық білімі яғни пәнді қаншалықты меңгергендігі және қалай оқығандығының маңызы зор. Себебі, биологтар үшін математикалық білім тек биологиялық статистиканы (биометрияны) нақтырағы бақылау және эксперимент арқылы алынған заңдылықтар нәтижесін өңдеудің математикалық әдістерін үйренумен шектелмейді.
Заманауи биологияда математиканың мынадай бөлімдері тірі объектінің құрылымы туралы ұғым қалыптастыруда кеңінен қолданылады: ықтималдықтар теориясы мен математикалық статистика, дифференциалдық теңдеулер теориясы, дифференциалдық геометрия және жиындар теориясы. Сондықтан «Биология» мамандығы бойынша математика пәнінен типтік бағдарламада (22. 06. 2006 ж. ) студентке мынадай білім негіздерін игеру талап етіледі:
Логикалық және алгоритмдік ойлау деңгейін жетілдіре отырып, математика пәні бойынша алған білімін биологиялық есептерді шешуде қолдана білуі тиіс.
Ықтималдықтар теориясы мен математикалық статистикаға негізделген биологияда жиі қолданылатын деректерді өңдеу тәсілдерін игеріп, олардың қолдану облыстарын жете меңгеруі тиіс. Жалпыға міндетті кәсіптік жоғары білім стандарты бойынша көрсетілген тарауларды оқып үйрену теориялық және қолданбалы биологияның топырақтану, экология, генетика, биогеоцентология биохимия, биофизика, физиология, ботаника, зоология және микробиология салаларында қолдануға негізделген.
Математиканы оқытуда оның практикалық жағы маңызды болғандықтан биологтар мыналарды білуі тиіс:
- математикалық есептерді қоя білу;
- үйренілетін құбылыстардың математикалық моделін сауатты құра білу;
- Зерттеудің сапалы математикалық әдістерін таңдай білу және қолдана алу;
- Заманауи есептеу машиналарын пайдаланып сауатты есептеулер жүргізе білу;
- Алынған нәтижелерді болжам жасауға және шешім қабылдауға пайдалана білу.
Математикалық моделдердің көмегі арқылы математика өзімізді қоршаған ортада өтетін процестерді зерттеу мүмкіндігін береді, ал модельдеудің негізгі кезеңдері есептің қойылу шарты мен мақсатына қарай анықталады. Есептің қойылымында берілген бастапқы мәліметтермен қатар мақсатын анықтау және объектіні немесе процесті талдау анық көрсетілуі қажет. Ең бастысы модельдеу объектісін анықтап, нәтижеде не болу керектігін түсіну қажет. Модельдеудің нәтижесі мәселені (есепті) түсіну нәтижесіне байланысты.
Сондықтан биологиядағы математикалық модельді үш топқа бөлуге болады.
1. Регрессиялық модель - объектіге әсер ету нәтижесінде оның сипаттамасының өзгерісін зерттеуге арналған есептер (формулалар, дифференциалды теңдеулер, статистикалық заңдар) және объект белгілі бір параметрлерді қанағаттандыру үшін оған қалай әсер ету керектігін анықтау. Мысалы жапырақтардағы оттегінің жұтылу жылдамдығы мына формуламен сипатталады:
Мұндағы Y -0, 25г оттегінің 1 сағ. ішінде жұтылуы, D-күндер саны, В-ылғалдың пайыздық мөлшері, Т-температура. Бұл формула эксперимент жүргізген белгіленген күндердегі температура мен ылғалдықтарды өлшеу арқылы оттегінің жұтылу жылдамдығын анықтауға мүмкіндік береді [4] .
2. Имитациялық модель - физиологиялық процесстерді сипаттау моделі. Мұның классикалық мысалы ретінде биомакромолекуланы құрайтын, атомдарының импульсы, координаталары белгілі және өзара әрекеттесу заңдылықтарын сипаттайтын молекулярлық динамика моделін алуға болады. Бұл модель өсімдіктердің өнімділігін арттыру процестерін сипаттауда кеңінен қолданылады (бидайды өндіруде жоғары көрсеткіштерге жету, мақтаның біркелкі өсіп жетілуі, жоғары сортты алманың өнімділігін арттыру т. с. с. )
3. Сапалық (негізгі) модель. Кез келген ғылымда аналитикалық зерттеулерге және табиғат құбылыстарын сипаттайтын қасиеттеріне негізделген жай модельдер бар. Бұл моделдерді сапалық модель деп атаймыз. Мысалы, қояндардың популяциясының немесе клеткалар популяциясының көбею жылдамдығы олардың санына пропорционал екендігі олардың өсіп- өну қабілетін сипаттайды. Мұны математикалық түрде дифференциал теңдеулер арқылы жазайық:
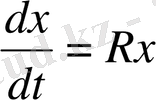 (1)
(1)
Популяциясының көбею жылдамдығының популяция санына пропорционалдығы туралы болжамын ХVIII-ғасырда Томас Роберт Мальтус (1766-1834) «Халық санының өсуі туралы» (1798) -деген кітабында айтқан. (1) -заңына сәйкес, егер пропорционалдық коэффициент R=r=сonst (Мальтус болжағандай) болса, популяция саны экспонент бойынша шексіз өсе береді

яғни Мальтус өз жұмыстарында бұл заңдылық нәтижесі бойынша азық-түлік өнімдері, басқа тауарлар өсуі сызықты, ал экспоненциал түрде көбейетін популяция жойылатындығын (азықтың жетіспеушілігінен) көрсеткен. В. Вольтерра «бір-біріне дұшпан» екі түрдің бір ортада өмір сүруі туралы гипотезаларынан олардың өзара әрекеттерінің математикалық моделін яғни «Жыртқыштар және жемтіктер» деп аталатын моделін мына түрде жазуға болатындығын көрсетті: [1]
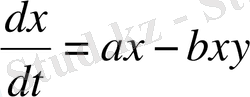
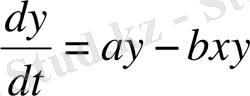
«Жоғары математика» тек бастапқы курстарда оқытылатындықтан (5В05007 - биология мамандығы, 3-кредит, 135 сағ. ) биологиялық есептердің математикалық моделін құруды қарапайым мысалдар арқылы түсіндіру тиімді.
Мысалы. Бактериялар популяциясының өскендігі соншалықты оның t уақыттағы өсу жылдамдығы популяция мөлшерін 10-ға бөлгенге тең. Осы құбылыстың математикалық моделін құрыңыз [3] .
Нақты жүйе. Қайсыбір түрдің популяциясында тіршілік процесі жүріп жатыр.
Есептің қойылымы. Популяция санының уақытқа байланысты өзгеру заңдылығын табу керек.
Негізгі жорамалдар.
а) Қайсыбір түрдің популяциясының көбею және жойылу процестерінің жылдамдығы сол уақыт мезетіндегі олардың санына пропорционал.
б) Биохимиялық және физиологиялық процестер есепке алынбайды.
в) Олардың арасында келіспеушілік жоқ (орналасу кеңістігі, қоректену ортасы үшін)
г) Бір ғана түрдің популяциясы қарастырылады.
Модель құру. Мынадай белгілеулер енгіземіз:
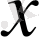 -арқылы
-арқылы
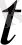 уақыт ішіндегі популяция санын,
уақыт ішіндегі популяция санын,
 -көбею жылдамдығы,
-көбею жылдамдығы,
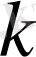 - көбею коэффициенті,
- көбею коэффициенті,
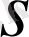 -табиғи жойылу жылдамдығы,
-табиғи жойылу жылдамдығы,
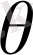 -жойылу коэффициенті,
-жойылу коэффициенті,
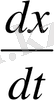 - популяция санының өзгеру жылдамдығы,
- популяция санының өзгеру жылдамдығы,
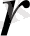 -өсу коэффициенті.
-өсу коэффициенті.
Барлық ескерілетін жағдайлар орындалса, онда популяция санының табиғи өсу моделін (Мальтус моделін) аламыз және
 ,
,
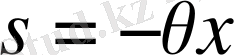 екендігін ескеріп, түр санының уақыт бірлігі ішіндегі өзгерісі пайда болған және осы уақыт ішінде жойылғандар санымен анықталады:
екендігін ескеріп, түр санының уақыт бірлігі ішіндегі өзгерісі пайда болған және осы уақыт ішінде жойылғандар санымен анықталады:
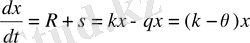 . немесе
. немесе
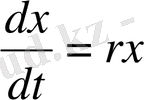 .
.
Бастапқы
 уақытта түр саны
уақытта түр саны
 деп есептеп дифференциалдық теңдеуді шешсек:
деп есептеп дифференциалдық теңдеуді шешсек:

Енді осы модельдің нақты объектіге (түп нұсқаға) сәйкестігін тексерелік.
Егер

 болса, яғни жойылу жылдамдығы көбею жылдамдығынан артық болғанда, түрдің саны біртіндеп 0-ге тең болады.
болса, яғни жойылу жылдамдығы көбею жылдамдығынан артық болғанда, түрдің саны біртіндеп 0-ге тең болады.
Егер

 болса, яғни жойылу жылдамдығы көбею жылдамдығынан аз болғанда, түрдің саны уақытқа байланысты шексіз өседі.
болса, яғни жойылу жылдамдығы көбею жылдамдығынан аз болғанда, түрдің саны уақытқа байланысты шексіз өседі.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz