Сигналдар және оның математикалық сипаттамалары
Жұмыс түрі: Реферат
Тегін: Антиплагиат
Көлемі: 14 бет
Таңдаулыға:
Мазмұны
Кіріспе
Сигнал спектрі - бұл қосындысы сигнал құрайтын жиіліктің, амплитуданың және бастапқы фазалардың нақты мәндері бар гармоникалық құрамалар жиынтығы. Теориялық түрде сигнал спектрі шексіз, сондықтан практикада спектрі f 1 ≤ f ≤ f 2 жиілік жолағымен шектелген сигналдардың математикалық моделін қолданадады. Сигналдың спектр кеңжолағы деп сигнал қуатының басатын бөлігі шоғырланған, минималды жиілік жолағы аталады.
Спектр кеңжолағы - бұл сигнал спектрі орын алатын жиілік интервалы; сигнал спектрінің максималды және минималды жиіліктерінің айырмасымен есептеледі.
1 Сигналдар және оның математикалық сипаттамалары
1. 1 Сигналдар мен кездейсоқ процестер
Байланыс теориясында хабарлама көзі көптеген мүмкін хабарламалар арасынан таңдау жасайтын құрылғы ретінде қарастырылады. Әрбір нақтылы хабарлама орындау(таңдамалы функция) белгілі бір ықтималдықпен туындайды. Ықтималдық өлшемі берілген көпшілік, ансамбль деп аталады. Хабарламалар мен сигналдар ансамбльдері шектіжәне шексіз болуы мүмкін.
Осылайша, хабарламалар, сигналдар, бөгеуілдер кездейсоқ процестер болып табылады және оларды зерттеуде кездейсоқ процестер теориясының негізгі нұсқауларықолданылады. Уақыттың кездейсоқ емес функциясы детерминалданған деп аталады.
Кездейсоқ процесс t : t 1 , t 2 , …мәндерінің дискретті көпшілігінде берілуі мүмкін; мұндай кездейсоқ процестер кездейсоқ тізбектер деп аталады. Кездейсоқ функциянытек ықтималдық мәнде ғана беруге болады. Егер кездейсоқ процестің немесе { X(t k ) } уақыт функциясы ансамблінің реализациялау саны шекті болса, онда олардыңықтималдығын көрсету жеткілікті.
Көбіне уақыттың бүкіл осінде немесе соңғы бөлігінде берілген, уақыт бойынша үзіліссіз процестер жиі кездеседі. Уақыттың соңғы бөлігінде берілген процестер финитті деп аталады.
n тәуелсіз элементтерінің (Бернулли тізбегі) кездейсоқ тізбегінің қарапайым түрі келесідей түрде болады:
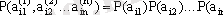
мұндағы Р - элмент ықтималдығы.
Тәуелді элементтердің кездейсоқ тізбегінің маңызды түрі болып Марков тізбегі табылады. Бұл кейбір a ik элементінің пайда болуының шартты ықтималдығы, егер алдыңғы a i, k-1 элементі белгілі болса, толығымен анықталған тізбек. Бұл дегеніміз:
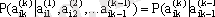
мұндағы
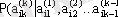- алдыңғы моменттерде
a
i1
,
a
i2
, . .
a
ik-1
бөлігінің реализациясы жүзеге асырылды деген шартпен
a
ik
элементінің
t
k
уақыт моментінде пайда болуыныңшартты ықтималдығы.
Марковтың қарапайым тізбегінде тізбектес элементтер арасындағы байланыс көршілес элементтер арасындағы тәуелдікпен анықталады.
Жалпы жағдайда X(t) скалярлы кездейсоқ процесі толығымен берілген, егер кез келген t 1 , t 2 , . . t n уақыт моменттері және кез келген x 1 , x 2 , x n мәндері үшін көрсетілгенуақыт моменттерінде X(t) сәйкесінше x 1 , x 2 , . . x n мәндерінен аспайтын мәндер қабылдайтынын есептеуге болса, онда:
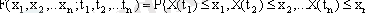
мұндағы: P{…} - оқиғаның біріккен ықтималдығы;
X(t n ) - t n моментіндегі кездейсоқ процестің қиылысы;
F (x 1 , x 2 , x n ) функциясы - процесс ықтималдығының n -өлшемді таралу функциясы;
x 1 , x 2 , x n - аргументтер;
t 1 , t 2 , . . t n - параметрлер.
Кездейсоқ процесс толығымен берілген, егер кез келген n және кез келген t 1 , t 2 , . . t n моменттері үшін таралу функциясын табуға мүмкін болса. 1. 1 суретте кейбір кездейсоқ процестің төрт реализациясы (оның үш қиылысы) көрсетілген.
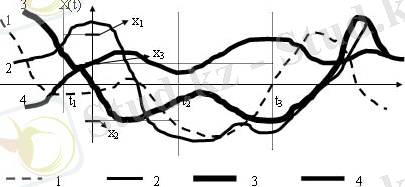
1. 1- Сурет - Кездейсоқ процестің реализациясы
1 және 2 реализацилары X(t 1 ) ≤ x 1 , X(t 2 ) ≤ x 2 , X(t 3 ) ≤ x 3 шарттарын қанағаттандырады, мұндағы x 1 , x 2 , x 3 - қиылыс мәндері. 3 және 4 реализациялары бұл шарттарды қанағаттандырмайды. Егер бұл процесте басқа реализациялар болмаса, онда үшөлшемді таралу функциясы берілген қиылыстарда 1 және 2 реализацияларының ықтималдықтарының қосындысына тең.
Егер барлық x k бойынша меншік туынды функциялар болса, онда ықтималдықтың n -өлшемді таралу тығыздығын анықтауға болады:
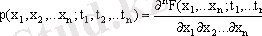
ол процесті толығымен анықтайды, егер ол кез келген қылыстың кез келген саны үшін белгілі болса.
Кездейсоқ процестер әр типті болады. Дискретті және үзіліссіз процестер болады. Дискретті процесс үшін Х кездейсоқ шамасы үзіліссіз процесс үшін тек көптеген x 1 , x 2 , x 3 шекті мәндерін қабылдай алады:
- кез келген интервалдан алынған кез келген х мәндерін, тіпті шексіз де. Кездейсоқ шамаларды математикалық сипаттау үшін келесідей кездейсоқ емес негізгі статистикалық сипаттамалар енгізіледі:
- Ықтималдықтың таралу функциясы: F(x) =X ≤ x кездейсоқ шаманың мәндері белгілі бір таңдап алынған х мәнінен аспайтынының ықтималдығын көрсетеді. Егер кездейсоқ шама х дискретті сәндер қабылдаса, онда F(x) - дискретті функция. Егер Х - үзіліссіз кездейсоқ шама болса, онда F(x) - монотонды өспелі функция, оның мәндері 0 ≤ F(x) ≤ 1 интервал аралығында жатыр және F(- ∞) =0 , F(∞) =1
- Ықтималдықтың таралу тығыздығы, ол p(x) =dF(x) /dx таралу функцисының туындысынан есептеп алынады. Физикалық түрде p(x) - бұл кездейсоқ шаманың х нүктесі маңындағы dx аз интервалына түсуі.
- Математикалық күту - бұл келесідей ансамбль бойынша процестің орташа мәні:
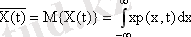
мұндағы
p(x, t)
-
t
қиысы үшін біркелкі таралу тығыздығы. Кездейсоқ процес пен оның математикалық күтуінің арасындаңы айырма центрленген процес деп аталадыжәне
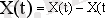деп белгіленеді.
- Центрленген процес квадратының математикалық күтуі дисперсия деп аталады:
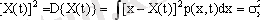
Дисперсия сандық жағынан орташа мәнге қатысты нәтижелердің шашылу дәрежесін сипаттайды. Физикалық мәні жағынан σ x - бұл орташа квадратты ауытқу (тиімдімағына) . Сонымен қатар кездейсоқ процесті сипаттау үшін қолданылады:
- Корреляция функциясы ( t 1 және t 2 уақыт моменттерінің фунекциясы) центрленген кездейсоқ процестің екі қиысының көбейтіндісінің математикалық күтуі сияқтыанықталады:
Бұл корреляция функциясын өзара корреляция функциясынан X(t) және Y(t) процестері арасындағы) ажырата білу керек:
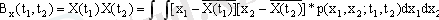
Математикалық күтуі мен дисперсиясы уақыттан тәуелсіз, ал корреляция функциясы t 1 - t 2 = τ айырмасынан тәуелді кездейсоқ процесті стационарлы деп атайды.
- Қуаттың спектрлі тығыздығы - кездейсоқ процестің жиілік бойынша қуат таралуын көрсетеді, кез келген жиілікте келесідей анықталады:
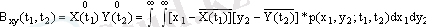
мұндағы Δ P - Δ f жиілік жолағына келетін, кездейсоқ процестің қуаты. [1]
1. 2 Сигналдың математикалық моделі
Көптеген жағдайларда уақыт диаграммасының (сурет. 1. 2) көмегімен электробайланыс сигналын уақыт бойында өзгеретін электрлі шама (ток, кернеу, электромагнитті тербеліс, өріс кернеулігі) ретінде қарастырады.
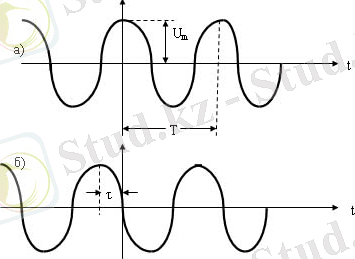
1. 2 - Сурет - Гармоникалық тербеліс
Сигналдармен барлық мүмкін есептерді жүргізу үшін сигналдың математикалық сипаттамасы болу керек. Сигналдың математикалық сипаттамасы оның математикалық моделі деп аталады. Мысалы, гармоникалық тербелістің (сурет 1. 2) бөлігін келесі түрде жазуға болады:
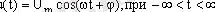
мұндағы U m - максималды мән (амплитуда) ;
ω - бұрыштық жылдамдық;
ω = 2 π f ,
мұндағы f - циклдік жиілік ( f=1/T ) ;
φ - бастапқы фаза.
Фаза бойынша жылжу (сурет 1. 2, б) гармоникалық тербелістің τ уақытына жылжуына әкеледі.
Импулсьті сигнал деп шектеулі уақытта нөлден өзгеше сигналдар аталады. Байланыс техникасында бейнеимпульстар мен радиоимпульстар деп екіге бөледі. 1. 3 суретте импульсті сигналдар мен олардың параметрлері көрсетілген.
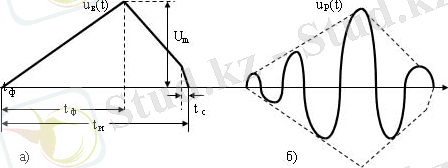
1. 3- Сурет - Импульсті сигналдар:
а) бейнеимпульс; б) радиоимпульс.
Радиоимпульстің математикалық моделі:
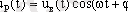
мұндағы U в (t) - бұл айнала қоршаушы;
cos(wt + φ 0 ) - толтыру функция.
Видеоимпульстің параметрлері болып табылатындар: U m - амплитуда;
t и - импульс ұзақтығы;
t ф - фронт ұзақтығы;
t c - басылу ұзақтығы.
Электробайланыста көбіне жалғыз импульстар мен қолданылады.
Импульстердің периодты тізбегі үшін қосымша параметр- құбырлылық енгізіледі:
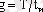
Шексіз амплитуданың шексіз қысқа видеоимпульсі дельта-функция ( σ - функция) деп аталады, ол келесідей түрде жазылады:
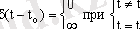
мұндағы t 0 - импульстің әсер ету моменті.
Күрделі сигналдарды элементарлы (қарапайым) базисті функциялар қатары түрінде көрсетуге болады. Мысалы, периодты сигналдарды математикалық көрсету үшін Фурье қатарын қолданады, онда базисті функция ретінде еселі жиіліктердің (гармоникалар) гармоникалық (синусоидалы және косинусоидалы) тербелістер таңдалыпалынады:
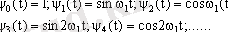
мұндағы ω 1 =2 π /T - функция тізбегінің бұрыштық жиілігі (бірінші гармоника) . Гармоникалық тербелістің бөлігін келесі түрде жазуға болады:
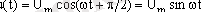
Барлық нақты периодты сигналдар Дирихле шарттарын қанағаттандырады, сондықтан оларды Фурье қатары түрінде көрсетуге болады:
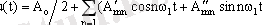
мұндағы коэфициенттер:
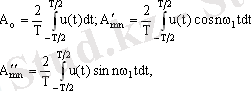
немесе:
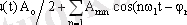
мұндағы:
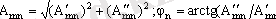
Немесе комплексті формада (Фурье интегралы) :[2]
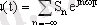
мұндағы:
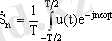
1. 3 Кездейсоқ сигналдар спектрлері
Спектральді диаграмма деп осы сигналдың Фурье қатарының графикалық коэфициенттерінің графикалық бейнелеуін айтады. Диаграммаларды амплитудалы және фазалы деп бөледі. Гармоникалар амплитудалары тек оң мәндер, ал фзалар - - π ≤ φ n ≤ π интервалындағы оң және теріс мәндер қабылдайды.
Сигнал спектрі - бұл қосындысы сигнал құрайтын жиіліктің, амплитуданың және бастапқы фазалардың нақты мәндері бар гармоникалық құрамалар жиынтығы. Теориялық түрде сигнал спектрі шексіз, сондықтан практикада спектрі f 1 ≤ f ≤ f 2 жиілік жолағымен шектелген сигналдардың математикалық моделін қолданадады. Сигналдың спектр кеңжолағы деп сигнал қуатының басатын бөлігі шоғырланған, минималды жиілік жолағы аталады.
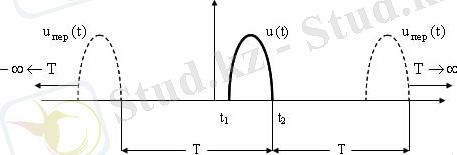
2. 4- Сурет - Импульсті сигнал және оның периодты жалғасы
Мұндай шекті ауысу кезінде w 1 = 2π / T T сигналдың негізгі бөлігі нөлге ұмтылады, спектральді қосымшалар саны шексіз өседі. nw 1 және (n + 1) w 1 көршілес гармоникалар жиіліктері спектр тұтастай етіп бір біріне өте жақын орналасады. Мұндай жағдайда спектрді есептеу үшін Фурье қатарының жазудың комплексті формасын қолданады:
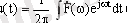
мұндағы
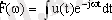
Комплексті спектральді тығыздық:
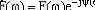
мұндағы F(w) - модуль немесе амплитулардың спектральді тығыздығы (амплитудалы спектр) ;
ψ(w) периодты емес сигналдың аргументі немесе фазалы спектрі.
Соңғы ( t 1 , t 2 ) интервалда берілген периодты емес (импульсті) сигналдарды спектральді көрсету үшін тікелей Фурье қатарын қолануға болмайды, себебі импульсті синал периодты емес. Сигналды гармоникалық орналастыру үшін келесілер орындалады:
- u (t) импульсті сигналы периодтыға дейін ( t 1 , t 2 ) аралығы кіретін кез келген Т периодпен толықтырылады;
- алынған u пер (t) периодты сигнал Фурье қатары түрінде көрсетіледі;
- содан кейін T → ∞ болғандағы u пер (t) дан u (t) ға дейін шекті ауысу орындалады;
1. 4 суретте импульсті сигналдың периодты жалғасына мысал көрсетілген.
Модуль - бұл жұп функция, аргумент - тақ функция. n -ші гармониканың амплитудасы:
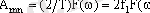
Яғни, периодты емес сигналдың амплитудаларының спектральді тығыздығы және берілген сигналдың қайталануынан алынған периодты тізбектің сызықты спектрініңайнала қоршаушысы, формасы бойынша сәйкес келеді, тек масштабында ғана айырмашылық бар. T → ∞ болғанда:
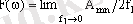
... жалғасы
Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.
Ақпарат
Қосымша
Email: info@stud.kz