Қатты дене деформациясы

Қатты дененің деформациясы

Қатты денелердің құрылысы кристалдық тор түрінде болады да, оны құрайтын бөлшектер белгілі ретпен орналасады. Әрбір бөлшекке оған жақын орналасқан екіншісі әсері, сөйтіп осы бөлшектердің қорытқы күші нольге тең болғанда, дене тепе-теңдік күйде болады. Сыртқы күштің әсерінен бөлшектер алғашқы қалпынан ығысады да, дене өзінің формасы мен мөлшерін өзгертеді, яғни деформацияланады.

Сыртқы күштің әсері тоқталғаннан кейін дененің мөлшері мен формасы бастапқы қалпына оралса, оны серпімді деформация деп атайды.

Сыртқы күштің әсері тоқталғаннан кейін дененің деформациясы сақталса, оны пластикалық немесе қалдық деформация деп атайды.

Сыртқы күштің шамасы аз болғанмен ұзақ уақыт бойы әсер етсе, онда серпімді деформация қалдық деформацияға ауысады. Ақиқат денелерге пластикалық деформация тән, өйткені сыртқы күштің әсері тоқтағаннан кейін де дене бастапқы қалпына келе алмайды. Бірақ қалдық (пластикалық) деформация аз болса, оны ескермей денені серпімді деформацияланған деп қарастырады.

Серпімділік дәрежесі деформациялаушы күштің әсерін тоқтатуға қажет жұмыс пен сол денені деформациялайтын жұмыстың қатынасына тең.

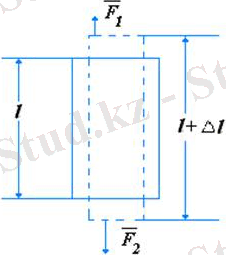
4. 11 - сурет

Серпімді деформацияланған денені ойша екіге бөлейік. Осы бөліктерге әсер етуші барлық сыртқы күштердің қорытқы күші, бөліктердің бір-біріне әсер ететін серпімді күшімен теңгеріледі. 4. 11 - суретте біртекті жіңішке сымның ұзындығы да, 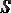оның қима ауданы. 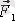және 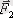оның ұштарына қарама-қарсы бағытта әсер ететін күштер, күштер әсерінен өзгерген сымның ұзындығы. Созылу деформациясы үшін оң мәнді, сығылу үшін теріс мәнді.

Сымның бірлік ауданына 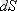келетін серпімді күштің сан мәніне тең шаманы механикалық кернеу деп атайды

(4. 20)

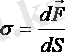
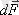күш 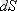ауданға перпендикуляр бағытта әсер етсе кернеуді нормаль (перпендикуляр), жанама бағытта әсер етсе тангенциал (жанама) деп атайды.

Дененің формасы не сызықтық мөлшерінің өзгеруін салыстырмалы деформацияны анықтайды. Сымның ұзындығының салыстырмалы өзгеруі (бойлық деформация) деп абсолют деформацияның сымның бастапқы ұзыдығына қатынасын айтады :

(4. 21)

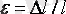
Сымның енінің салыстырмалы ұзаруы (сығылу деформациясы)

(4. 22)

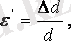
мұнда 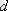- бастапқы ені, 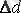- енінің өзгеруі.

Ағылшын физигі Р. Гук (1635 - 1703 жж. ) заңы бойынша серпімді деформацияланған дененің кернеуі оның салыстырмалы деформациясына тура пропорционал болады. Оны тәжірибе жүзінде дәлелдеп, математикалық түрде:

(4. 23)

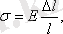
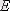- серпімділік модулінің шамасы дененің затына тәуелді. Деформацияның түріне қарай оның аты да, шамасы да өзгереді.

Серпімділік модуліне кері шаманы серпімділік коэффициенті деп атайды

.

(4. 24)

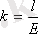Гук заңы мөлшерлі салыстырмалы деформацияланған денелер үшін орындалады.

Кернеу мен деформацияның бір-біріне пропорционалдығы бұзылатын кернеу мәнін 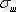пропорционалдық шегі деп атайды. (4. 12 - сурет. А нүктесі) .

Біз деформацияның қарапайым түрі - созылу немесе сығылуды қарастырайық.

Бойлық созылу кезінде сымның серпімді күші оны созушы күшке 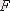тең болса, онда дене деформацияланбайды. Бұл кезде серпімділік модулін 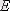Юнг модулі деп атайды.

(4. 20), (4. 21), (4. 22) формулаларды ескеріп төмендегіше жазамыз:

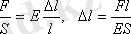немесе

(4. 25)

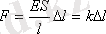
(4. 26) өрнегі Гук заңының басқаша түрін сипаттайды да, серпімді деформацияланған сымның ұзаруы оған әсер ететі күшке тура пропорционал деп оқылады.

Соңғы формуладан болғанда, яғни Юнг модулі механикалық кернеуге тең.

Сығылу кезінде де ұзындыөтың қысқарып деформациялануы (4. 26) формуламен өрнектеледі.

Дененің созылуы (немесе сығылуы) кезінде оның ені қысқарады (ұзарады) . Енінің салыстырмалы қысқаруының, бойлық ұзаруға қатынасын Пуассон коэффициенті 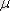деп атайды:

(4. 26)

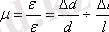
Қатты дененің деформациясы механикалық кернеудің белгілі мәніне дейін Гук заңына бағынады. Созылған темір сымның деформациясы мен кернеуінің арасындағы байланысты диаграмма арқылы көрсетейік:

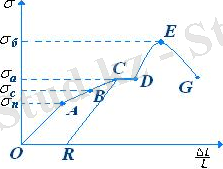
4. 12 - сурет

Деформация шамасы аз мөлшерде болғанда -ның мәні 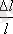-ге тура пропорционал. Гук заңы орындалатын сызықтық байланысқа сәйкес кернеудің мәнін пропорционалдық шегі 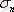деп атайды. Суретте ол 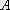нүктесіне сәйкес. Кернеуді арттырсақ деформация әлі де серпімді, бірақ тәуелділігі сызықтық байланыста болмайды ( 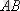қисығы) .

Олай болса қалдық деформация байқалмайтын кернеудің мәнін серпімділік шегі 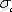деп атайды, оған 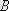нүктесі сәйкес. Кернеуді арттырмасақ та салыстырмалы деформацияның өсуіне сәйкес келетін( түзуі) кернеу мәнін аққыштық шегі 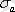дейді ( нүкте) . Аққыштығы ұзаққа созылатын материалдар тұтқыр, аққыштық қасиет байқалмайтындар морт деп аталады. Дененің үзіліп кетуіне дейін шыдайтын кернеудің ең үлкен мәнін ( 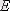нүктесіне сәйкес) беріктік шегі 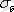немесе уақытша кедергі деп атайды. 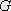нүктесінде дене үзіледі.

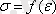
Деформацияланған денеге түсірілетін кернеуді азайтсақ, онда кернеу мен салыстырмалы ұзару арасындағы график түзуіне параллель кесіндімен сипатталады да, абцисса осін 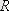нүктеде қияды. 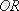кесінді қалдық деформацияға сәйкес.

Қатты денелер әрқашанда өздерiнiң сыртқы пiшiндерiн сақтап тұра алмайды. Сыртқы күштердiң әсерiнен олардың геометриясы мен көлемi өзгеруi мүмкiн.

Сыртқы күштердiң әсер етуiнiң нәтижесiнде дененiң сыртқы пiшiнi мен көлемiнiң өзгеруi деформация деп аталады

Дененiң әртүрлi бөлшектерi сыртқы күштердiң әсерiнен әртүрлi орын ауыстыру жасайтын болса, онда ол жағдайда қашанда деформация пайда болады. Сыртқы күштердiң әсерi тоқтатылғаннан кейiн жоғалып кететiн деформациялар - серпiмдi деформациялар деп, ал жоғалмайтын деформациялар- пластикалық деформациялар деп аталады.

Сығылу және созылу деформациясы. Егер бiртектi металл стерженнiң екi ұшына шамасы жағынан тең, бағыттары жағынан қарама - қарсы күштермен әсер етсек, онда стерженнiң деформациясы созылу деформациясы деп аталады

Созылу деформациясы мынадай екi шамамен сипатталады:

абсолюттi

Δl = l - l ₀

және салыстырмалы

ε = Δl / l ₀

ұзарулары, мұндағы l ₀ - стерженнiң бастапқы ұзындығы, ал l - соңғы ұзындығы.

Егер осы стерженге бiр - бiрiне бетпе-бет бағытталған күштермен әсер етсек, онда стержень сығылу деформациясына ұшырайды Бұл жағдайда абсолюттiк және салыстырмалы ұзарулар терiс таңбалы болады.

Көптеген қатты денелердiң деформациялары аз ғана созылуға және сығылуға ұшырағанда ( Δl << l ₀ ) серпiмдi болып келедi.

Жылжу деформациясы. Деформацияның бұл түрi, тiк қабаттар белгiлi бiр бұрышқа бұрылғанда, жазық қабаттардың өзара бiр-бiрiмен параллель күйде жылжуымен сипатталады.

Дене қабаттарының бiр-бiрiмен салыстырмалы түрде ығысуына әкелiп соғатын деформацияны жылжу деформациясы деп атаймыз.

Үлкен бұрыштарға жылжуы дененiң сынуына - сызаттың пайда болуына әкелiп соғады. Ол қайшымен, қашаумен және т. б. жұмыс iстеген кезде пайда болады.

---

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.

• Іс жүргізу
• Автоматтандыру, Техника
• Алғашқы әскери дайындық
• Астрономия
• Ауыл шаруашылығы
• Банк ісі
• Бизнесті бағалау
• Биология
• Бухгалтерлік іс
• Валеология
• Ветеринария
• География
• Геология, Геофизика, Геодезия
• Дін
• Ет, сүт, шарап өнімдері
• Жалпы тарих
• Жер кадастрі, Жылжымайтын мүлік
• Журналистика
• Информатика
• Кеден ісі
• Маркетинг
• Математика, Геометрия
• Медицина
• Мемлекеттік басқару
• Менеджмент
• Мұнай, Газ
• Мұрағат ісі
• Мәдениеттану
• ОБЖ (Основы безопасности жизнедеятельности)
• Педагогика
• Полиграфия
• Психология
• Салық
• Саясаттану
• Сақтандыру
• Сертификаттау, стандарттау
• Социология, Демография
• Спорт
• Статистика
• Тілтану, Филология
• Тарихи тұлғалар
• Тау-кен ісі
• Транспорт
• Туризм
• Физика
• Философия
• Халықаралық қатынастар
• Химия
• Экология, Қоршаған ортаны қорғау
• Экономика
• Экономикалық география
• Электротехника
• Қазақстан тарихы
• Қаржы
• Құрылыс
• Құқық, Криминалистика
• Әдебиет
• Өнер, музыка
• Өнеркәсіп, Өндіріс