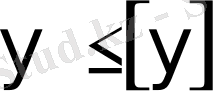Күрделі қарсыласу

Пән: Физика
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 8 бет
Таңдаулыға:

Дәріс -10. Күрделі қарсыласу

Инженерлік практикада қарапайым деформацияланған конструкция элементтерінен гөрі күрделі деформацияланған (күрделі қарсыласатын) элементтер жиі кездеседі. Күрделі деформацияланған элементтердің қималарында бір емес бірнеше ішкі факторлар пайда болады. Ішкі факторлардың түрлеріне байланысты күрделі деформациялар келесі түрлерге ажыратылады.

1. Қиғаш иілу . Қиғаш иілген элементтің көлденең қималарында Q _y , M _x Q _x , M _y ішкі факторлары пайда болады.

2. Центрден тыс созылу (сығылу) . Центрден тыс созылган (сығылған) элементтердің көлденең қималарында M _x , M _y ию моменттерімен қатар N _z , бойлық күш пайда болады. Жеке жағдайларда ию моменттерінің бірі нөлге тең болуы мүмкін.

3. Иіліп бұралу. Иіліп бұралған машина бөлшектерінің қималарында Q _x , Q _y көлденең күштері мен M _x , M _y ию, М _z бұраушы моменттері пайда болады.

Жалпы жағдайда стерженьдердің көлденењ қималарында кез келген ішкі факторлар пайда болуы мүмкін.

Күрделі деформацияның жеке түрлерімен танысайык.

1. Қиғаш иілу

Басты жазықтықтардан басқа, бойлық өс арқылы өтетін, кез келген жазықтықтарда жатқан сыртқы күштердің әсерінен конструкция элементі қиғаш иіледі. Қиғаш иілген арқалықты беріктікке есептеу тәртібі келесі мысалда көрсетілген. Бір ұшы қатаң бекітілген арқалықтың екінші ұшына Р күші әсер етсін. Күштің әсер ету сызығы x өсімен бұрышын жасап өтетіндіктен арқалық қиғаш иіледі (1, а-сурет) . Сыртқы күшті басты өстерге проекциялап құраушыларын табайық

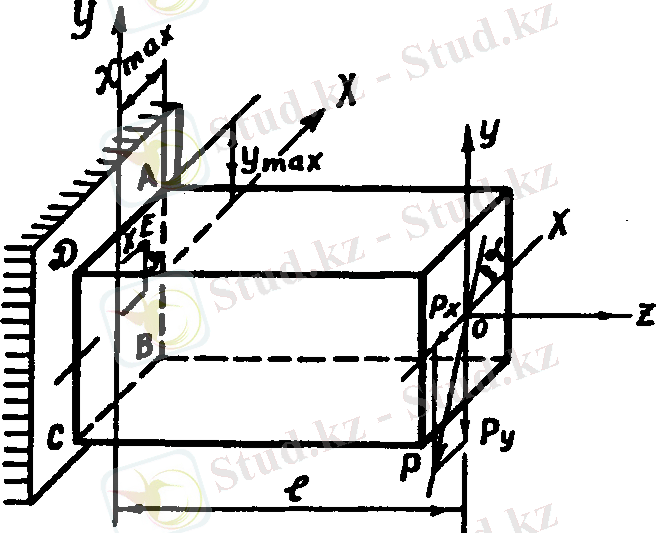Құраушы Р _х , Р _у күштерінің әсерінен берілген арқалық өзара перпендикуляр басты жазықтықтарда жазық иіліп, көлденең қималарыңда июші моменттер пайда болады

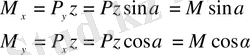
мұндағы M = Pz.

Тұғыр қимасында жатқан Е нүктесіндегі кернеуді табу үшін күш әрекеттерінің тәуелсіздік приціпін пайдаланамыз (1, а-сурет) . Вертикаль жазықтықтағы М _х -тің әсерінен Е нүктесінде пайда болған кернеу

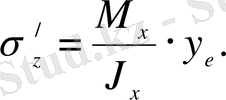
Горизонталь жазықтықтағы М _у -тің әсерінен пайда болған кернеу

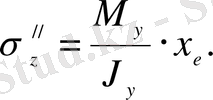
Нүктедегі толық кернеу

(1)

немесе

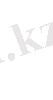
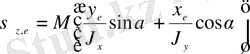
мұндағы х _е , у _е - Е нүктесінің координаталары.

Алынған (1) формуланы пайдаланып кез келген пішінді қиманың нүктелеріндегі кернеулерді анықтауға болады. Бұл формуладағы, бірінші квадранттың нүктелерінде созушы кернеу тудыратын июші моменттер оң таңбалы деп қарастырылып, ал нүктелерінің координаттары өз таңбаларымен жазылады. Нүктелерінде тек созушы кернеулер пайда болатын квадрант бірінші квадрант ретінде қабылданады.

Қимадағы кернеулер х, у координаттына тәуелді болғандықтан, қауіпті қимадағы ең үлкен созушы кернеу әсер етіп тұрған бұрыштағы А мен ең үлкен сығушы кернеу әсер етіп тұрған бұрыштағы С нүктелері қауіпті болып саналады.

Арқалықтың беріктігін А нүктесі үшін беріктік шартын құрып тексереміз

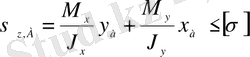
мұндағы х _а = х _max , y _a =y _max болғандықтан

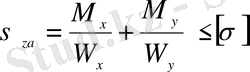
Бұрыштардағы А, С нүктелеріндегі кернеулердің абсолют шамалары бірдей.

Арқалық морт материалдан жасалса, оның беріктігі A нүктесімен қатар С нүктесі бойынша да тексеріледі.

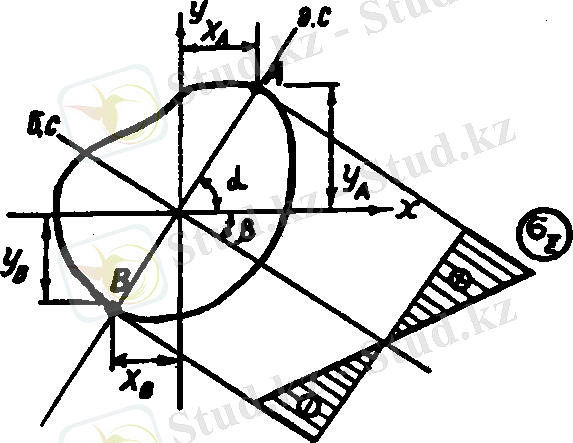Енді бұрышы жоқ 2-суреттегі қиманы қарастырайық. Қиманың қауіпті нүктелерін табу үшін алдымен бейтарап сызықтың орны анықталады. Бейтарап сызық, тік кернеуі нөлге тек нүктелердің геометриялық орны. Олай болса, кернеудің шамасын (1) нөлге теңестіріп, координаттар басы арқылы өтетін, бейтарап сызықтың теңдеуін аламыз

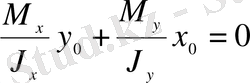
мұндағы х ₀ , у ₀ - бейтарап өс нүктелерінің айнымалы координаттары.

Бұл теңдеуді 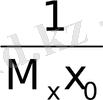шамасына көбейтіп келесі түрге келтірейік:

(2)

Енді 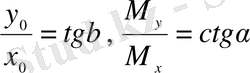екенін ескеріп, бейтарап сызықтың орнын анықтайтын формуланы аламыз

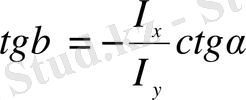. (3)

Бейтарап сызықтың x өсіне қарағандағы бұрышы теріс таңбалы болғандықтан, ол сағат тілі бағыты бойымен салынып П, IV квадранттар арқылы өтеді (2-сурет) .

Алынға3) теңдеуінде 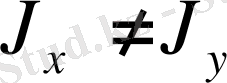болғандықтан, 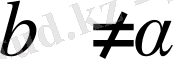. Демек, сыртқы күштің әсер ету сызығы (ә. с) мен бейтарап сызық (б. с. ) өзара перпендикуляр емес (2-сурет) .

Қиманың контурына, бейтарап сызыққа параллель жанамалар жүргізіп қауіпті А, В нүктелерін табамыз (2-сурет) . Суреттегі кернеудің эпюрі ежелгі тәртіппен салынған.

Қауіпті нүктелер үшін беріктік шарты келесі түрде жазылады

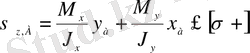(4)

(5)

Конструкция элементтерінің көлденең қималары дөңгелек, квадрат пішінді болса, J _x =J _y .

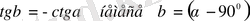Яғни, сыртқы күштің әсер ету сызығы мен бейтарап сызық өзара перпендикуляр. Әсер ету сызығы координаттар жүйесінің бас нүктесі арқылы өтетін кез келген күштің әсерінен мұндай аркалықтар жазық иіледі.

Сыртқы күш пен қауіпсіз кернеу белгілі болса, қиғаш иілген арқалықтың қима өлшемдерін беріктік шартынан келесі тәртіппен анықтайды қиманың өлшемдері алдын ала белгілі деп қарастырылып қандайда бір мәндері (4) теңсіздігіне енгізіледі.

Есептеліп анықталған теңсіздіктің сол жағы оң жағына қарағанда айтарлықтай кіші болса, қима өлшемдерін үлкейтіп, ал айтарлықтай үлкен болса кішірейтіп аркалықтың беріктігі қайта тексеріледі. Тексеру теңсіздіктің сол жағы мен оң жағының арасындағы айырым 4-5%-ке жуықтағанша қайталанады.

Қиғаш иілген арқалықтың деформациясы, иілу өсінің дифференциалдық теңдеуін интегралдау немесе басқа әдістермен анықталады. Ол үшін күш әсерлерінің тәуелсіздік принципі пайдаланылып, қиғаш иілу бас жазықтықтардағы екі жазық иілудің қосындысы ретінде қарастырылады. Қиғаш иілген арқалықтың кез келген қимасындағы ойысу, бас жазықтықтардағы ойысулардың геометриялық қосындысына тең

(6)

мұндағы y _вер - вертикаль жазықтықтағы ойысу, у _гор - горизонталь жазықтықтағы ойысу. Қатаңдық шарты келесі түрде жазылады

мұндағы [у] - қауіпсіз ойысу.

Қиғаш иілген арқалықтың серпімді сызығы мен сыртқы күштің әсер ету сызығы әр түрлі өс жазықтықтарында жатады. Ойысу мен күш бағыттары өзара сәйкес келмейді.

2. Орталықтан тыс созылу (сығылу)

Орталықтан тыс созылу (сығылу) деп қиманың ауырлық орталығынан басқа кез келген нүкте арқылы берілетін, бойлық өске параллель күштің әсерінен сырықтың деформациялануын айтады (3-сурет) .

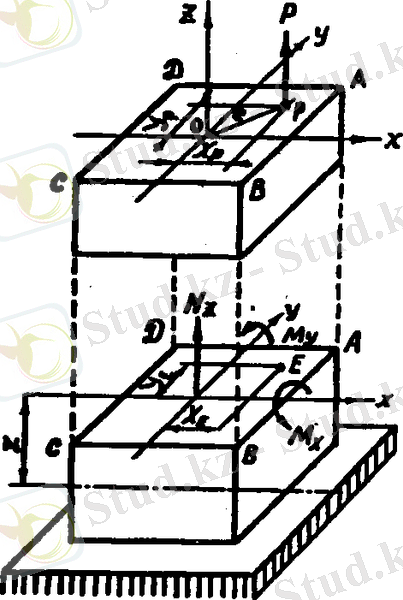Күш түскен нүкте (р) полюс деп аталады. Полюстің координаталарын х _р , у _р арқылы белгілейік. Полюстен координаттар жүйесінің басына дейінгі ара қашықтық эксцентриситет деп аталып, е арқылы белгіленеді. Орталықтан тыс созылған сырықтың кез келген қималарында N _z = Р, М _x = Ру _p , М _y = Рх _p ішкі факторлары пайда болады (3-сурет) .

Берілген қиманың Е нүктесіндегі кернеуді анықтайық. Күш әрекеттерінің тәуелсіздік принципі бойынша N _z бойлық күшінің

әсерінен 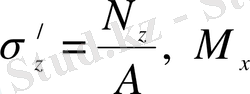- июші моменттің әсерінен 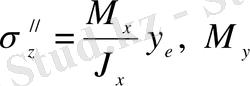- июші моменттің әсерінен 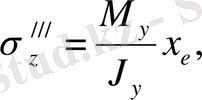тік кернеулері пайда болады.

Сонымен Е нүктесіндегі қорытынды кернеу

(7)

Алынған (7) формуласымен қиманың кез келген нүктесіндегі кернеуді табуға болады. Кернеудің таңбасын дұрыс анықтау үшін полюс жаткан квадрант бірінші квадрант деп қарастырылып, ішкі факторлар мен нүктенің координаталары (7) формуласына өз таңбаларымен енгізіледі. Бірінші квадранттағы нүктелерде созушы кернеулер тудыратын июші моменттер оң таңбалы деп саналады.

Қауіпті кернеулер бұрыштағы A, C нүктелерінде пайда болады. Соңдықтан сырықтың беріктігі А нүктесі үшін жазылған беріктік шарты бойынша тексеріледі

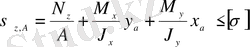
немесе

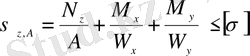мұндағы х _a , y _a - A нүктесінің координаталары.

Морт материалдардан жасалған брустар тек созушы емес ең үлкен сығушы кернеу бойынша да тексеріледі

Енді бұрыштық нүктелері жоқ 4-суретіндегі қиманы қарастырайық. Бұрыштық нүктелері жоқ қиманың қауіпті нүктелерін табу үшін алдымен бейтарап сызықтың орны анықталады. Бейтарап сызықтың бойында жатқан нүктелерде кернеу нөлге тең. Олай болса

(8а)

Мұндағы х _б , y _б - бейтарап сызық нүктелерінің айнымалы координаталары. Есептің бастапқы шарты бойынша, 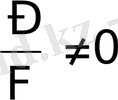болғандықтан

(8б)

Енді х _б , y _б координаталарын кезекпен нөлге теңестіріп, X пен У осьтерінің бейтарап сызықпен қиылған кесінділерін табамыз

(9)

Кесінділерді (таңбаларын ескеріп) X, Ү осьтеріне өлшеп салып, алынған m, n нүктелері арқылы бейтарап сызықты жүргіземіз (4-сурет) . Суретте, бейтарап сызық (б. с. ) арқылы белгіленген. Бейтарап сызық координата осьтерін бірінші квадрантқа қарсы үшінші квадрант арқылы қиып өтеді. Қиманың контур бейтарап сызыққа параллель, жанамалар жүргізіп қауіпті А, нүктелерін табамыз.

Қауіпті нүктелер үшін беріктік шарты келесі түрде жазылады

(10)

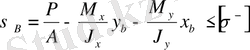(11)

Мұндағы х _а , у _а - А нүктесінің координаталары, х _б , y _б- -B нүктесінің координаталары.

Кернеудің (7) формуласы бойынша салынған эпюрі 4- суретте көрсетілген.

Қима өзегі . Алынған (9) формуласы бойынша, бейтарап сызық координаттар басы (қиманың ауырлық орталығы) арқылы өтпейді. Сыртқы күштің эксцентриситеті неғұрлым үлкен болса, бейтарап сызық координаттар басына соғұрлым жақын, неғұрлым кіші болса - соғұрлым алыс. Эксцентриситет нөлге тең болғанда бейтарап сызық пен координаттар басы ара қашықтығы шексіздікке ұмтылып, сырық Орталық созылу деформациясына ұшырайды.

Бейтарап сызықтың бұл қасиеті инженерлік практикада кеңінен қолданылады. Морт материалдардың көбісінің сығылуға қарағанда созылуға қарсыласу қабілеті төмен екені бізге белгілі. Бетон, тас, күйдірілгген қыш сияқты материалдардан жасалған азаматтық немесе өндірістік құрылыс элементтерінде, шамасы мардымсыз, созушы кернеулердің пайда болуы сыну қаупін туғызуы мүмкін. Соңдықтан мұндай құрылыс элементтері үшін қима ядросы тұрғызылады.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.