Дәріс 15. Динамикалық күштер: Даламбер принципі, динамикалық еселік және соққыға есептеу


Дәріс 15. Динамикалық күштер
Күш нөлден бастап соңғы шамасына жеткенше баяу өсіп, соңында тұрақты болып қалатын болса, статикалык күш деп аталады. Статикалык күш әсер еткен конструкцияның үдеуі мардымсыз болғандықтан, инерция күші нөлге тең.
Шамасы жылдам өзгеретін күш динамикалық күш деп аталады. Динамикалық күштің әсерінен конструкция иемесе оның элементтері елеулі тербелістерге ұшырап, тербеліс жылдамдығының өзгеруіне байланысты жүйеде массасы мен үдеуінің көбейтіндісіне тең инерция күші пайда болады. Бұл күш бастапқы күшке қарағаңда бірнеше есе үлкен болуы мүмкін. Динамикалық күштер, соққы, айнымалы кайталанбалы т. б. күштерге ажыратылады. Машина бөлшектерін динамикалық күшке есептеу статикалық күшке есептеуге карағаңда әлдеқайда күрделі.
Конструкция элементін динамикалық күшке есептеу үшін теориялық механикадан белгілі, Даламбер принципі қолданылады. Бұл принцип бойынша қозғалыстағы кез келген денені сыртқы және инерция күштерінің әсерінен кандай да бір мезетте лездік тепе-теңдік болады деп қарастыруға болады. Егер жүйенін инерция күшін анықтауға мүмкіншілік жоқ болса (мысалы соққы күші әсер еткенде), ішкі күштерді, деформацияны анықтау үшін энергияның сақталу заңы қолданылады. Динамикалық күштердің әсерінен материалдардың механикалық касиеттері өзгереді. Мысалы, статикалық күштің әсерінен материалдар пластикалық қасиет көрсетсе, динамикалық (соққы) күштің әсерінен морттық қасиет көрсетуі мүмкін, т. с. с.
 Бір қалыпты үдемелі қозғалған машина бөлшектерін беріктікке есептеу
Бір қалыпты үдемелі қозғалған машина бөлшектерін беріктікке есептеу
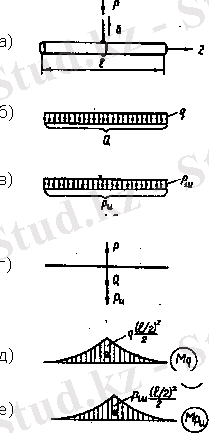
Кранның болат сымнан есілген арқанына ілінген брус сыртқы Р күшінің әсерінен y өсінің бағытында бірқалыпты үдемелі қозғалыста болсын (1, а-сурет) . Динамикалық күш әсерінен сырық үлкен деформацияға ұшырамайды, қатаңдығы жеткілікті деп қарастырайық. Сырыққа сыртқы Р күшінен басқа көлемінде бірқалыпты таралған, карқындылығы q -ға тең өзінің салмағы Q = ql инерциялық күш Р и әсер етеді. Есептеу сүлбелері күштердің әрқайсысы үшін 1, б, в, г-суреттерде жеке көрсетілген.
Ұзындығы бірге тең брус бөлігінің инерциялық күші келесі формуламен анықталады
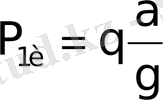
Статиканың келесі теңдеуін құрайық
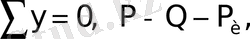 бұдан
бұдан

Енді июші мометтің эпюрін салып (1, д, е-сурет), сырықтың ортасыңдағы күш түскен қима қауіпті екенін көреміз.
Қауіпті қимада
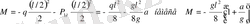
Мұндағы
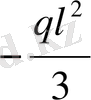 қауіпті кимадағы статикалық июші момент екенін ескерсек,
қауіпті кимадағы статикалық июші момент екенін ескерсек,
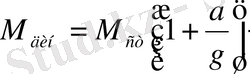 болады. Демек, динамикалық июші момент статикалық июші моменттен
болады. Демек, динамикалық июші момент статикалық июші моменттен
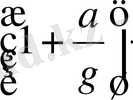 есе үлкен. Жақшадағы шаманы к
дин
арқылы белгілеп, динамикалық еселік деп атайды.
есе үлкен. Жақшадағы шаманы к
дин
арқылы белгілеп, динамикалық еселік деп атайды.
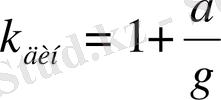
Сырықтың қауіпті қимасындагы ең үлкен тік кернеуі

Беріктік шарты:
 .
.
 Алдыңғы мысалда иілген сырықты қарастырдық. Енді сыртқы Р күшінің әсерінен
z
өсінің бағытында бірқалыпты үдемелі қозғалған сырықты беріктікке есептейік (2-сурет) . Сырыққа төменгі ұшына ілінген дененің салмағы Q мен инерциялық күші
Алдыңғы мысалда иілген сырықты қарастырдық. Енді сыртқы Р күшінің әсерінен
z
өсінің бағытында бірқалыпты үдемелі қозғалған сырықты беріктікке есептейік (2-сурет) . Сырыққа төменгі ұшына ілінген дененің салмағы Q мен инерциялық күші
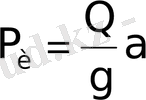 . әсер етеді. Қозғалыстың үдеуі
z
өсімен бағыттас болғандықтан, инерциялық күш кері бағытталған. Сырықтың көлденең қимасындағы кернеулерді анықтау үшін оны қималар тәсілі бойынша А - А жазықтығымен қиып статиканың теңдеуін құрайық
. әсер етеді. Қозғалыстың үдеуі
z
өсімен бағыттас болғандықтан, инерциялық күш кері бағытталған. Сырықтың көлденең қимасындағы кернеулерді анықтау үшін оны қималар тәсілі бойынша А - А жазықтығымен қиып статиканың теңдеуін құрайық

мұндағы N
дин
=
 Equation. 3
А
- көлденең қимасының ауданы.
Equation. 3
А
- көлденең қимасының ауданы.
Олай болса
 .
.
Енді
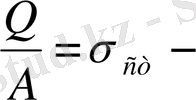 статикалық кернеу екенін ескерсек,
статикалық кернеу екенін ескерсек,
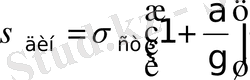
мұндағы
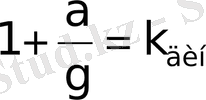 динамикалық еселік.
динамикалық еселік.
Сонымен, бірқалыпты үдемелі қозғалыстағы машина бөлшегінің кез келген нүктесіндегі динамикалық кернеу, сол нүктедегі статикалық кернеуді динамикалық еселікке көбейткенге тең.
Соғылған сырықты беріктікке есептеу
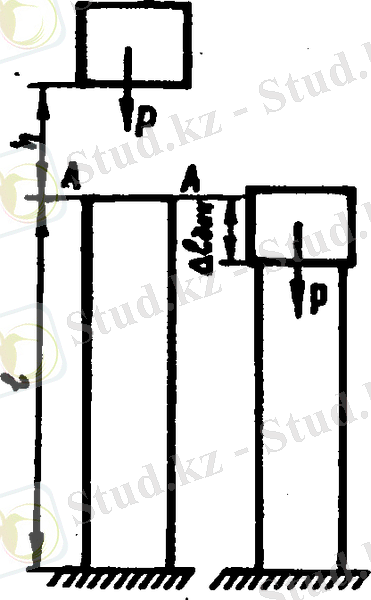 Бір ұшы қатаң бекітілген вертикаль брустың жоғарғы ұшына (қимасына)
h
биіктігінен белгілі бір жылдамдықпен салмағы
Р
-ға тең жүк құлап түссін (3-сурет) . Мұңдай құбылыс соққы деп аталады. Құлаған дененің сырыққа жанасқан мезетіне сәйкес келетін жылдамдық келесі формуламен анықталады
Бір ұшы қатаң бекітілген вертикаль брустың жоғарғы ұшына (қимасына)
h
биіктігінен белгілі бір жылдамдықпен салмағы
Р
-ға тең жүк құлап түссін (3-сурет) . Мұңдай құбылыс соққы деп аталады. Құлаған дененің сырыққа жанасқан мезетіне сәйкес келетін жылдамдық келесі формуламен анықталады
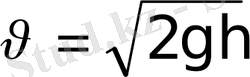 .
.
Жоғарыдан құлаған дене сырықтың A-А қимасына жанасқаннан кейін, шамасы өте аз
 с уакыттың ішінде жылдамдығынан ажырап, үдеуі кенеттен артып кетеді.
с уакыттың ішінде жылдамдығынан ажырап, үдеуі кенеттен артып кетеді.
Үдеудің өзгеру заңдылығын анықтау өте күрделі болғаңдықтан, инерциялық күштің шамасын анықтау да өте күрделі. Сондықтан, соғылған машина бөлшектеріндегі кернеу мен деформацияны табу үшін Даламбер принципі емес, энергияның сақталу заңы қолданылады. Соққыға есептеу теориясы келесі жорамалдарға негізделіп құрылады.
Соғылған машина бөлшегі есептелгенде, оның көлеміңдегі кернеу пропорционалдық шектен кіші, деформациясы серпімді, ал олардың арасыңдағы тәуелділік Гук заңына бағынады деп қарастырылады. Соққыға ұшыраған жүйенің нүктелерінің динамикалық орын ауыстыру шамаларының қатынастары статикалық орын ауыстыру шамаларының қатынастарымен бірдей. Мысалы, шамалары бірдей статикалық және динамикалық күштердің әсеріне ұшыраған арқалық үшін келесі пропорцияны құруға болады (4, а, б-сурет) .
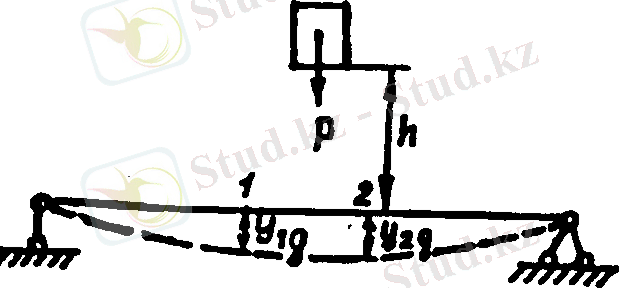
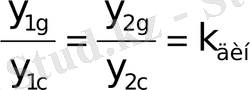
мұндағы y 1g , у 1c , y 2g , y 2c - бірінші, екінші нүктелердің статикалық және динамикалық орын ауыстыру шамалары. Арқалықтың серпімді өстері өзара ұқсас (4, а, б-сурет) .
Жүйенің соққы тиген жеріндегі нүктесінің қозғалыс жылдамдығы нөлге теңелген мезетте басқа нүктелерінің де жылдамдығы нөлге теңеледі.
Осы жорамалдарға сүйеніп 3-суретте көрсетілген сырықтың кернеуі мен деформациясын анықтайық. Соғушы дененің
h
биіктігінен құлағандағы жасайтын жұмысы (3-сурет)
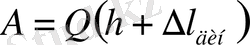 , мұндағы
, мұндағы
 -соғушы және соғылушы денелердің жанасу нүктесінің орын ауыстыру шамасы (сырықтың абсолют қыскаруы)
-соғушы және соғылушы денелердің жанасу нүктесінің орын ауыстыру шамасы (сырықтың абсолют қыскаруы)
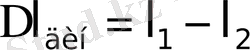
Ішкі күш арқылы өрнектелген деформацияның потенциялық энергиясы
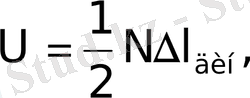 Equation. 3 мұндағы
Equation. 3 мұндағы

Энергияның сақталу заңы бойынша сыртқы күштің (салмақтың) жасаған жұмысы деформацияның потенциялық энергиясына тең

Енді (2) пропорциясы бойынша
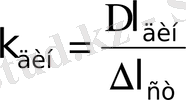 екенін ескерсек,
екенін ескерсек,
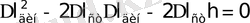
Алынған екінші дәрежелі тендеуді шешіп;
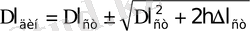
түбірдің оң таңбасын қалдырамыз; өйткені теріс таңба есептің физикалық мағынасына қайшы келеді.
Олай болса,

мұндағы
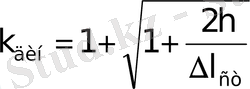
Сол сияқты динамикалық кернеу статикалық кернеуді динамикалық еселікке көбейткенге тең
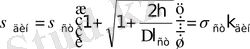
Енді жеке жағдайларды қарастырайық.
1. Машина бөлшегіне лездік соққы күші әсер етсін (
h
=0) .
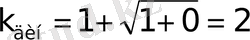 Демек,
Демек,
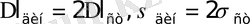
2. Соғушы дененің құлап түсетін биіктігі, сол дененің салмағындай күштің әсерінен соғылушы сырықта пайда болған абсолют ұзару (қысқару) шамасына қарағанда әлдеқайда үлкен болса, динамикалық еселік келесі формуламен анықталады
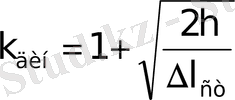
Соққы күштің әсерінен иілген сырықтардың динамикалық еселіктерін анықтау үшін (3) формуласындағы
 орнына
y
дин
,
орнына
y
дин
,
 орнына
y
ст
бұралған сырықтар үшін
орнына
y
ст
бұралған сырықтар үшін
 орнына
орнына
 қойылады.
қойылады.
1-мысал. Кранның болат сымнан есілген арқанына ілінген жүк тұрақты
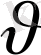 =1, 2 м/с жылдамдықпен төмен түсіп келе жатсын. Арқанның ұзындығы
l
= 8 м болғанда (арқан ілінген блоктан жүкке дейінгі ара қашықтық) жүк кілт тоқтатылды делік. Р = 5 кН. Арқанда пайда болған ең үлкен тік кернеуді анықтаңыз. Арқанның өз салмағы ескерілмейді. Қима ауданы А = 8 см
2
.
=1, 2 м/с жылдамдықпен төмен түсіп келе жатсын. Арқанның ұзындығы
l
= 8 м болғанда (арқан ілінген блоктан жүкке дейінгі ара қашықтық) жүк кілт тоқтатылды делік. Р = 5 кН. Арқанда пайда болған ең үлкен тік кернеуді анықтаңыз. Арқанның өз салмағы ескерілмейді. Қима ауданы А = 8 см
2
.
Ш е ш у і. Арқанда пайда болған кернеу келесі формула бойынша анықталады
 Мұндағы
Мұндағы
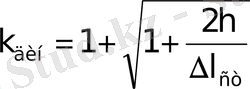 ,
,
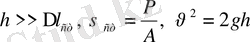 немесе
немесе
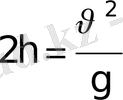 және
және
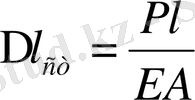 екенін ескерсек,
екенін ескерсек,
 .
.
Сонымен
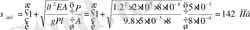
Негізгі әдебиеттер [1, 168-172 б. ], [2, 313-325 б. ], [3, 306-317 б. ] [4, 470-479 б. ]
Қосымша әдебиеттер [13]
Бақылау сұрақтары:
1. Динамикалық күштер деп қандай күштер аталады?
2. Даламбер принципі нені білдіреді?
3. Динамикалық күштер әсеріне есептегенде қандай алғышарттар қабылда-нады?
4. Динамикалық еселік нені сипаттайды?
5. Соққы теориясы қандай гипотезаға негізделген?
6. Күш соққы түрінде түсірілгенде материалдардық қасиеттері қалай өзгереді?
Дәріс 15. Динамикалық күштер
Күш нөлден бастап соңғы шамасына жеткенше баяу өсіп, соңында тұрақты болып қалатын болса, статикалык күш деп аталады. Статикалык күш әсер еткен конструкцияның үдеуі мардымсыз болғандықтан, инерция күші нөлге тең.
Шамасы жылдам өзгеретін күш динамикалық күш деп аталады. Динамикалық күштің әсерінен конструкция иемесе оның элементтері елеулі тербелістерге ұшырап, тербеліс жылдамдығының өзгеруіне байланысты жүйеде массасы мен үдеуінің көбейтіндісіне тең инерция күші пайда болады. Бұл күш бастапқы күшке қарағаңда бірнеше есе үлкен болуы мүмкін. Динамикалық күштер, соққы, айнымалы кайталанбалы т. б. күштерге ажыратылады. Машина бөлшектерін динамикалық күшке есептеу статикалық күшке есептеуге карағаңда әлдеқайда күрделі.
Конструкция элементін динамикалық күшке есептеу үшін теориялық механикадан белгілі, Даламбер принципі қолданылады. Бұл принцип бойынша қозғалыстағы кез келген денені сыртқы және инерция күштерінің әсерінен кандай да бір мезетте лездік тепе-теңдік болады деп қарастыруға болады. Егер жүйенін инерция күшін анықтауға мүмкіншілік жоқ болса (мысалы соққы күші әсер еткенде), ішкі күштерді, деформацияны анықтау үшін энергияның сақталу заңы қолданылады. Динамикалық күштердің әсерінен материалдардың механикалық касиеттері өзгереді. Мысалы, статикалық күштің әсерінен материалдар пластикалық қасиет көрсетсе, динамикалық (соққы) күштің әсерінен морттық қасиет көрсетуі мүмкін, т. с. с.
 Бір қалыпты үдемелі қозғалған машина бөлшектерін беріктікке есептеу
Бір қалыпты үдемелі қозғалған машина бөлшектерін беріктікке есептеу
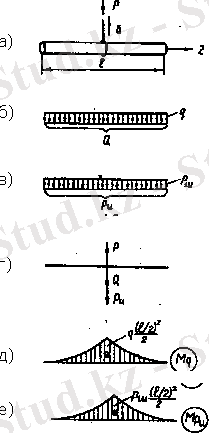
Кранның болат сымнан есілген арқанына ілінген брус сыртқы Р күшінің әсерінен y өсінің бағытында бірқалыпты үдемелі қозғалыста болсын (1, а-сурет) . Динамикалық күш әсерінен сырық үлкен деформацияға ұшырамайды, қатаңдығы жеткілікті деп қарастырайық. Сырыққа сыртқы Р күшінен басқа көлемінде бірқалыпты таралған, карқындылығы q -ға тең өзінің салмағы Q = ql инерциялық күш Р и әсер етеді. Есептеу сүлбелері күштердің әрқайсысы үшін 1, б, в, г-суреттерде жеке көрсетілген.
Ұзындығы бірге тең брус бөлігінің инерциялық күші келесі формуламен анықталады
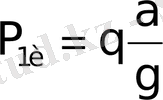
Статиканың келесі теңдеуін құрайық
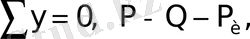 бұдан
бұдан

Енді июші мометтің эпюрін салып (1, д, е-сурет), сырықтың ортасыңдағы күш түскен қима қауіпті екенін көреміз.
Қауіпті қимада
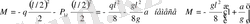
Мұндағы
 қауіпті кимадағы статикалық июші момент екенін ескерсек,
қауіпті кимадағы статикалық июші момент екенін ескерсек,
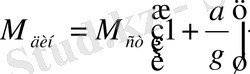 болады. Демек, динамикалық июші момент статикалық июші моменттен
болады. Демек, динамикалық июші момент статикалық июші моменттен
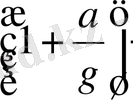 есе үлкен. Жақшадағы шаманы к
дин
арқылы белгілеп, динамикалық еселік деп атайды.
есе үлкен. Жақшадағы шаманы к
дин
арқылы белгілеп, динамикалық еселік деп атайды.
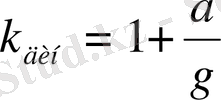
Сырықтың қауіпті қимасындагы ең үлкен тік кернеуі

Беріктік шарты:
 .
.
 Алдыңғы мысалда иілген сырықты қарастырдық. Енді сыртқы Р күшінің әсерінен
z
өсінің бағытында бірқалыпты үдемелі қозғалған сырықты беріктікке есептейік (2-сурет) . Сырыққа төменгі ұшына ілінген дененің салмағы Q мен инерциялық күші
Алдыңғы мысалда иілген сырықты қарастырдық. Енді сыртқы Р күшінің әсерінен
z
өсінің бағытында бірқалыпты үдемелі қозғалған сырықты беріктікке есептейік (2-сурет) . Сырыққа төменгі ұшына ілінген дененің салмағы Q мен инерциялық күші
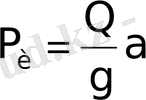 . әсер етеді. Қозғалыстың үдеуі
z
өсімен бағыттас болғандықтан, инерциялық күш кері бағытталған. Сырықтың көлденең қимасындағы кернеулерді анықтау үшін оны қималар тәсілі бойынша А - А жазықтығымен қиып статиканың теңдеуін құрайық
. әсер етеді. Қозғалыстың үдеуі
z
өсімен бағыттас болғандықтан, инерциялық күш кері бағытталған. Сырықтың көлденең қимасындағы кернеулерді анықтау үшін оны қималар тәсілі бойынша А - А жазықтығымен қиып статиканың теңдеуін құрайық

мұндағы N
дин
=
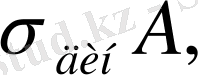 Equation. 3
А
- көлденең қимасының ауданы.
Equation. 3
А
- көлденең қимасының ауданы.
Олай болса
 .
.
Енді
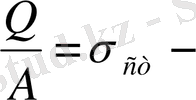 статикалық кернеу екенін ескерсек,
статикалық кернеу екенін ескерсек,

мұндағы
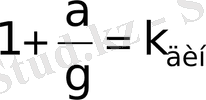 динамикалық еселік.
динамикалық еселік.
Сонымен, бірқалыпты үдемелі қозғалыстағы машина бөлшегінің кез келген нүктесіндегі динамикалық кернеу, сол нүктедегі статикалық кернеуді динамикалық еселікке көбейткенге тең.
Соғылған сырықты беріктікке есептеу
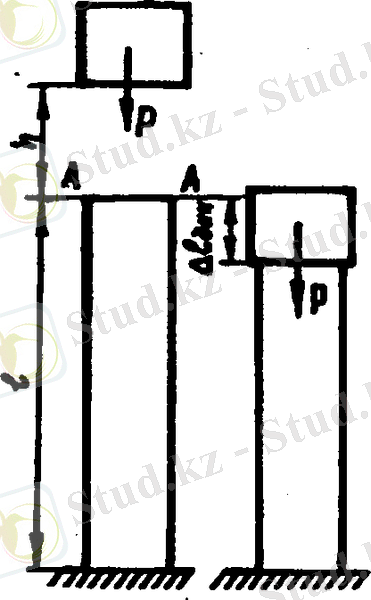 Бір ұшы қатаң бекітілген вертикаль брустың жоғарғы ұшына (қимасына)
h
биіктігінен белгілі бір жылдамдықпен салмағы
Р
-ға тең жүк құлап түссін (3-сурет) . Мұңдай құбылыс соққы деп аталады. Құлаған дененің сырыққа жанасқан мезетіне сәйкес келетін жылдамдық келесі формуламен анықталады
Бір ұшы қатаң бекітілген вертикаль брустың жоғарғы ұшына (қимасына)
h
биіктігінен белгілі бір жылдамдықпен салмағы
Р
-ға тең жүк құлап түссін (3-сурет) . Мұңдай құбылыс соққы деп аталады. Құлаған дененің сырыққа жанасқан мезетіне сәйкес келетін жылдамдық келесі формуламен анықталады
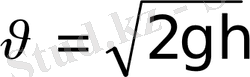 .
.
Жоғарыдан құлаған дене сырықтың A-А қимасына жанасқаннан кейін, шамасы өте аз
 с уакыттың ішінде жылдамдығынан ажырап, үдеуі кенеттен артып кетеді.
с уакыттың ішінде жылдамдығынан ажырап, үдеуі кенеттен артып кетеді.
Үдеудің өзгеру заңдылығын анықтау өте күрделі болғаңдықтан, инерциялық күштің шамасын анықтау да өте күрделі. Сондықтан, соғылған машина бөлшектеріндегі кернеу мен деформацияны табу үшін Даламбер принципі емес, энергияның сақталу заңы қолданылады. Соққыға есептеу теориясы келесі жорамалдарға негізделіп құрылады.
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz