Тұрақты токтың сызықты электр тізбектерін есептеу: контурлық тоқтар және түйіндік потенциалдар әдістері


2 ТҰРАҚТЫ ТОКТЫН СЫЗЫҚТЫ ЭЛЕКТР ТІЗБЕГІН ЕСПЕТСУ ӘДІСТЕРІ: КОНТУРЛЫҚ ТОКТАР ӘДІСІ ЖӘНЕ ТҮЙІҢДІ ПОТЕҢЦИАЛДАР ӘДІСІ
Тізбектерді Кирхгоф заңдарын қолданып есептегенде белгілі-бір реттілікті ұстанған жөн. Мысалы, 1. 1-суретте келтірілген тізбекте энергия (қорек) көздерінің ЭҚК-тері мен кернеулерінің және пассивті элементтерінің кедергілерінің сан мәндері белгілі де, токтарды, тізбек элементтерінің кернеулерін, қуаттарын және жұмыс әлпін анықтау керек болсын.
Әдетте токтардың нақты (шын) бағыттары белгісіз болатындықтан, алдымен олардың шартты оң бағыттары еркінше (қалауынша) таңдап алынады да, тізбектің электрлік схемасында стрелкамен көрсетіледі.
Бұдан кейін Кирхгофтың бірінші заңы бойынша бір түйіннен басқа түйіндер үшін теңдеулер жазылады. Қарастырып отырған тізбекте екі түйін бар, ендеше Кирхгофтың бірінші заңы бойынша бір теңдеу құру керек: a түйінінде
б түйінінде
Белгісіз шамаларды табу үшін құрылатын теңдеулер саны белгісіздер санына тең болуы шарт. Қарастырып отырған теңдеуде үш ток бар, ендеше өзара тәуелсіз үш теңдеу құру керек. Сондықтан қалған жетіспейтін теңдеулер Кирхгофтың екінші заңы бойынша тәуелсіз контурлар үшін жазылады.
Кирхгофтың екінші заңы бойынша теңдеулер жазу үшін контурларды айналып өту бағыты еркінше таңдап алынады. Қарастырылып отырған тізбекте бірінші және екінші контурларды сағат тілінің бағытында айналып өту қабылданған. Ал жалпы алғанда әртүрлі контурларды әртүрлі бағытта айналып өтуге болады. Контурларды айналып өткен кезде, егер кернеу көзінің кернеуі, ЭҚК және пассивті элементтегі ток, айналып өту бағытымен бағыттас болса, онда олар оң таңбамен, ал қарсы бағытта болса теріс таңбамен алынады.
бірінші контурында
екінші контурында
Құрылған теңдеулер жүйесі ретінде шешіліп, белгісіз токтар анықталады.
Теңдеулер жүйесінен токтар анықталған кезде, олардың бірқатары оң таңба, ал кейбіреулері теріс таңба қабылдайды. Бұл оң таңбалы токтардың шын бағыттарының еркінше алынған бағыттарымен бағыттас та, теріс таңбалы токтардың шын бағыттарының еркінше алынған бағыттарына қарсы бағытта екендігін көрсетеді.
Контурлық тоқтар әдісі. Кирхгофтың екінші заңына негізделген, сондықтан бұл әдіс бойынша теңдеулер саны Кирхгофтың екінші заңына бойынша қанша теңдеу құрастыру керек болса сонша теңдеу құрастырылады, яғни теңдеулер саны азаяды. Сонымен қатар екі жағдай қабылдаймыз.
а) электр тізбегінің контурларында бір біріне тәуелсіз, есептеуге арналған контурлық тоқтар өтіп жатыр б) тармақтардағы тоқтар осы тармақ арқылы тұйықталатын контурлық тоқтардың алгебралық суммасына тең болады.
Контурлық тоқтар әдісі көмегімен электр тізбектерін есептеуді төмендегі схема бойынша қарастырамыз. (сурет 2. 1)
Сурет 2. 1 - Контурлық тоқтар әдісінің иллюстрациясы
Берілген схема үшін Кирхгофтың екінші заңы бойынша қанша теңдеу құрастыратынын анықтаймыз: Кирхгофтың екі заңы бойынша барлық теңдеулер саны = белгісіз тоқтар санына тең =3 теңдеу.
Оның ішінен бірінші заң бойынша теңдеулер саны =түйін саны -1=2-1 =1 теңдеу. Қалған теңдеулер екінші заң бойынша жазылады. Сонымен контурлық тоқтар әдісі бойынша теңдеулер саны 2 теңдеу болады
R 1. 1 I 1. 1 + R 1. 2 I 2. 2 = E 1. 1 ; (2. 5)
R 2. 1 I 1. 1 + R 2. 2. I 2. 2 = E 2. 2 (2. 6)
мұндағы, I 1. 1 , I 2. 2 - контурлық тоқтар
R 1. 1 - бірінші контурдың өзіндік кедергісі, осы контурға кіретін барлық кедергілердің суммасына тең. Берілген схема үшін R 1. 1 =(R 1 +R 3 )
R 2. 2 - екінші контурдың өзіндік кедергісі, осы контурға кіретін барлық кедергілердің суммасына тең. Берілген схема үшін R 2. 2 =(R 2 +R 3 )
E 1. 1 - бірінші контурдың өзіндік ЭҚК-і, осы контурға кіретін барлық ЭҚК-нің суммасына тең. Берілген схема үшін Е 1. 1 =Е 1
E 2. 2 - екінші контурдың өзіндік ЭҚК-і, осы контурға кіретін барлық ЭҚК-нің суммасына тең. Берілген схема үшін Е 2. 2 =-Е 2
R 1. 2 = R 2. 1 - бірінші және екінші контурлар арасындағы өзара кедергі, теңдеуге минус таңбасымен жазылады. Берілген схема үшін
R 1. 2 = R 2. 1 = - R 3
Теңдеулер жүйесін шешіп, контурлық тоқтарды есептеледі. Теңдеулер жүйесін үшін матрицаларды қолданылады (Крамер әдісі) :
I 1. 1 = Δ 1 / Δ R ; I 2. 2 = Δ 2 / Δ R ; (2. 7)
мұндағы Δ R - теңдеу жүйесінің анықтауышы
Δ 1 анықтауышын табу үшін, жүйенің оң жағы бірінші бағананың орнына қойылады. Мысалы Δ 1 Δ 2 үшін:
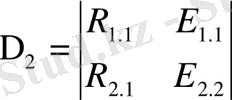 (2. 10)
(2. 10)
тармақтардағы тоқтарды табу үшін жоғарыда айтылған екінші жағдайды ескеру керек:
Төменде к теңдеулер жүйесі үшін Крамер әдісінің қолданылуы көрсетілген


 (2. 11)
(2. 11)
I 1. 1 = Δ 1 / Δ R ; I 2. 2 = Δ 2 / Δ R I n. n = Δ n / Δ R (2. 12)
Сызықтық тізбектер үшін өзаралық принциптің ( қайтымдылық теоремасы ) маңызы зор.
Ол бойынша: егер пассивті сызықтық тізбектің кез келген бір m тармағына орналасқан кернеу көзі, осы тізбектің басқа n тармағында k-мәнді тоқ туғызса, тап сол кернеу көзін керісінше n тармағына орналастырса, m тармағында тап сондай k-мәнді тоқ туғызады.
Түйіндік потенциалдар әдісі. Түйіндік потенциалдар әдісі Кирхгофтың бірінші заңына негізделген. Сондықтан, құрастырылатын теңдеулер саны Кирхгофтың бірінші заңы бойыншатеңдеулер санына тең болады, яғни: n - 1. Теңдеулерді тізбектің түйіндері үшін құрастырады.
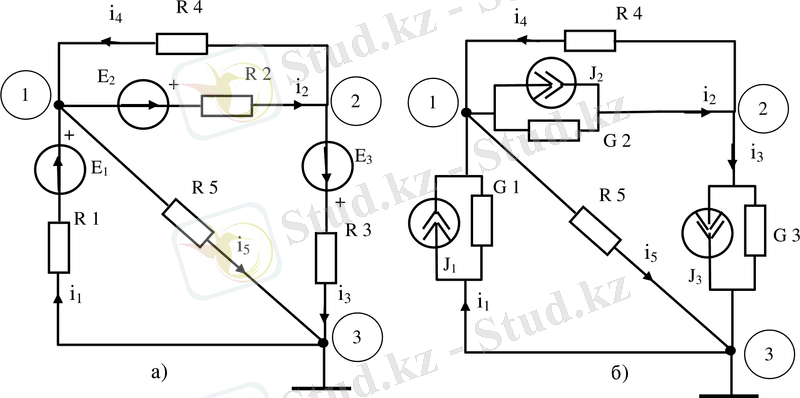
Сурет - 2. 2 Түйіндік потенциалдар әдісін сипаттайтын схема
а) бастапқы схема; б) кернеу көздерін тоқ көздеріне түрлендірген схема
G 11
-G 21
. . .
-G (n-1) 1
мұндағы, I 1. 1 , I 2. 2 , . . . , I n(n-1) - түйіндік тоқтар 1, 2, . . . , (n - 1) . Түйіндік тоқтар қарастырылып отырған түйінге жалғанған тармақатардағы ЭҚК көздерінің сол тармақтардың кедергісіне қатынастарының алгебралық суммасы болып табылады. Егер тармақтарда тоқ көздері болса онда олардың тоғы осы суммаға қосылады. Бұл суммаға ЭҚК көзі немесе тоқ көзі түйінге қарай бағытталса оң таңбамен, ал керісінше болса теріс таңбамен жазылады.
Мысалы бірінші түйін үшін:
2. 2 асуреттегі сұлба үшін I 1. 1 = (E 1 /R 1 ) - (E 2 /R 2 )
2. 2 б суреттегі схема үшін I 1. 1 = J 1 -J 2
G 11, G 22, G (n-1) (n-1), түйіндердің өзіндік өткізгіштіктері - қарастырылып отырған түйінге жалғанған барлық тармақтардың өткізгіштіктерінің суммасы
Мысалы 2. 2 а суреттегі схема үшін
G 11 = (1/R 1 ) + (E 2 /R 2 )
G 12, = G 21, G 1(n-1) = G (n-1) 1 түйіндердің өзара өткізгіштіктері -қарастырылып отырған екі түйінді жалғайтын тармақтардың өткізгіштіктерінің суммасы, минус таңбасымен алынады№
Мысалы 2. 2 а суреттегі сұлба үшін
G 12 = G 21 = - ((1/R 4 ) + (1/R 2 ) )
Теңдеулер жүйесін матрицалар көмегімен есептейді.
u 1 = Δ 1 / Δ G ; u 2 = Δ 2 / Δ G ; . . . ; u (n-1) =Δ (n-1) / Δ G , (2. 14)
мұндағы, Δ G - жүйенің негізгі анықтамасы:
 (2. 15)
(2. 15)
Δ 1 Δ 2 Δ (n-1) негізгі анықтауыштың бағаналарын теңдеудің оң жағымен ауыстырамыз.
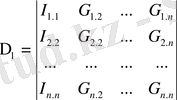

 (2. 16)
(2. 16)
Екі түйін әдісі. Бұл әдіс түйіндік потенциалдар әдісінің бір үрі болып табылады және ол тек қана екі түйіні бар тізбектерді есептеуге қолданады. Алдымен екі түйін арасындағы тұйінаралық кернеуді табады келесі формула бойынша:
мұндағы,
- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz