Электр тізбегінің теңдеулері

Пән: Электротехника
Жұмыс түрі: Материал
Тегін: Антиплагиат
Көлемі: 7 бет
Таңдаулыға:

түйіндері теңдеулер

Электр тізбегінің теңдеулерін тікелей шешуге негізделген есептеу әдісінің кемшілігі көптеген теңдеулермен жұмыс істеу қажеттілігі болып табылады. Осындай жүйедегі белгісіздер саны оңай төмендейді, компонент теңдеулерінің көмегімен, ағымдар немесе тармақтардың кернеулері, яғни әр тармақтың айнымалыларының негізі ретінде таңдалады. Дегенмен, бұл теңдеулер жүйесін шешу қажеттілігіне әкеледі, олардың саны филиалдардың санына тең.

Жиі негізде осындай негізде түйіндік кернеулер пайдаланылады - анықтамалық ретінде қабылданған бір түйінге қатысты тізбектік түйіндердің кернеуі. Q түйіндерімен байланыстырылған тізбек үшін, мұндай кернеулердің саны q - 1. Түйіндік теңдеулерді қалыптастыру үшін негіз Кирхгоф заңының теңдеуі болып табылады.

Түйін теңдеуін алу үшін G = 1 / R өткізгіштігін, EMF және ток көздерін қамтитын 0, 1 - 3 түйіндеріне қосылған тізбектің k-th түйінін (3. 1-сурет) қарастырыңыз.

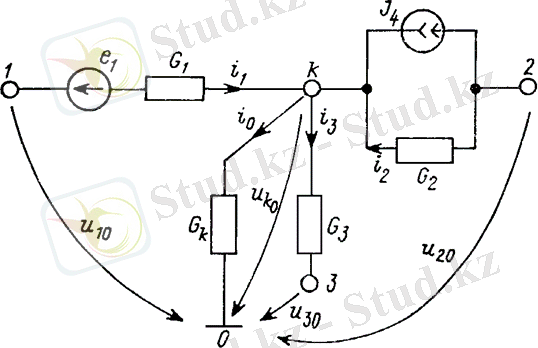
Суретте көрсетілген ток бағыттарын таңдағанда 3. 1, k-th түйініне арналған бірінші Кирхгоф заңының теңдеуі бар

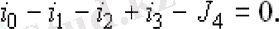
Түйіне қосылған филиалдардағы токтар туралы, u10, u20, u30 түйіндерінің кернеулері және G тармақтарының өткізгіштігі арқылы білдіріңіз:

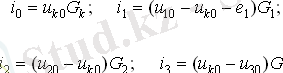
Терминдерді ауыстыру және топтау бірінші заңның формасына сәйкес келеді

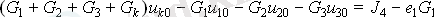
Жалпы алғанда, k-th торабы үшін түйін теңдеуі желілік алгебралық жүйелер үшін қабылданған өткізгіштігінің қос индексациясы арқылы жазылуы мүмкін:

G _k ₁ u ₁₀ + G _k ₂ u ₂₀ + . . . + G _kk u _k ₀ + . . . = J _k _у .

Қарастырылған мысалдан бастап, Gkk коэффициенті, k-th түйінінің ішкі өткізгіштігі, берілген түйінге қосылған барлық тармақтардың өткізгіштігінің сомасына тең. Gkm коэффициенті - k және m түйіндерінің өткізгіштігі - минус белгісімен алынған k және m түйіндеріне қосылатын тармақтардың өткізулерінің қосындысын білдіреді. Түйін теңдеуінің оң жағы - Jky түйіні - берілген түйінге бекітілген ағымдағы көздердің алгебралық сомасына тең. Құрамдас бөліктерде EMF e көздері, G өткізгіштері бар сериялармен байланыстырылған, түйін токтарында қарастырылып отырған композициялық саланың eG өнімі ретінде ескеріледі (G = ) үшін қолайлы EMF көздерімен филиалдардың болмауы. Түйіннің құрамдас бөліктері осы түйінге бағытталған көздер үшін плюс белгісімен және қарсы бағытта минус белгісімен алынады.

Осылайша, q түйіндер үшін q - 1 теңдеулер бар түйінімен q - 1 белгісіз - сызықтық алгебралық жүйесі, жалпы матрицаның нысаны бар

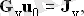
мұнда Gy - түйіндік өткізгіштердің шаршы матрицасы; u0 - түйіннің кернеу векторы; Джи - түйіндік токтардың векторы:

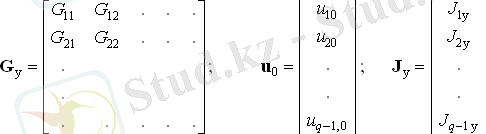
Пассивті тізбектің түйіндік өткізгіштерінің матрицасы симметриялы болып табылады - жалпы өткізгіштіктер бір-біріне теңестіріледі, олардың анықтамасы бойынша Gmk = Gkm.

3. 2. MATRIX NODE теңдеулерін жазу

Байланыстыруды, ЭМӨ-нің керемет көздерін және ток көзін (2. 2, a, b) қараңыз, құрамдас теңдеулер жалпы түрінде жазылуы мүмкін композиттік тармақтардың жиынтығы ретінде қарастырамыз.

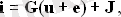
мұнда i, u, е, J - ағымдар, кернеулер, ЭМӨ көздері және композициялық тармақтардың ток векторлары; G = diag [G1, G2, . . . , Gn] - бұталардың өткізгіштігінің диагональды матрицасы.

Жоғарыда айтылғандай, біз ЭМҚ-ның керемет көздерімен (G = ) вирустық бұталардың жоқтығын қабылдаймыз. Үздіксіз ток көздері бар филиалдар тізбекте болуы мүмкін, өйткені оларда G = 0 бар.

Бірінші Кирхгоф заңын матрицалық түрде жаздық

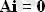
Бұдан әрі түйіннің кернеу векторы арқылы бұтақтардың кернеу векторын келесідей көрсетейік:

Шынында да, трансформацияланған матрица қатарында ең көбі екі нөл емес элементтер бар (1 және -1) . Сондықтан, түйіннің k-ден түйінге дейін бағдарланған р саны бар тармақтың кернеуі up = uk0-um0 айырмашылығы ретінде көрінеді, себебі p-ші қатарында тек екі нөл емес элементтері apk = 1 және apm = -1 болады.

Алынған байланыс бізге компонент теңдеуін формада жазуға мүмкіндік береді

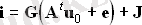
Бірінші Кирхгоф заңының матрицалық теңдеуіндегі оның алмастырылуы және матрицалық түйіндік теңдеуге көшу

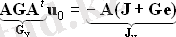
Осылайша, түйіндік өткізгіштігінің матрицасы қос матрицалық өнім және түйіндік токтардың векторы ретінде көрінеді.

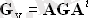
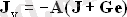
3. 3. ҰШҚЫҚ ЖЕРЛЕРДІҢ НОД ЕСЕБІНІҢ ФОРМАЦИЯСЫ

Түйін теңдеулерін құрастырған кезде, талданатын тізбектің түйіндерін нөмірлеу керек. Барлық басқа кернеулерді өлшейтін «0» көрсеткіші бар анықтамалық түйін ретінде, филиалдардың ең көп саны немесе жерге тұйықталған торап түйіні қосылған түйінді қабылдау ұсынылады.

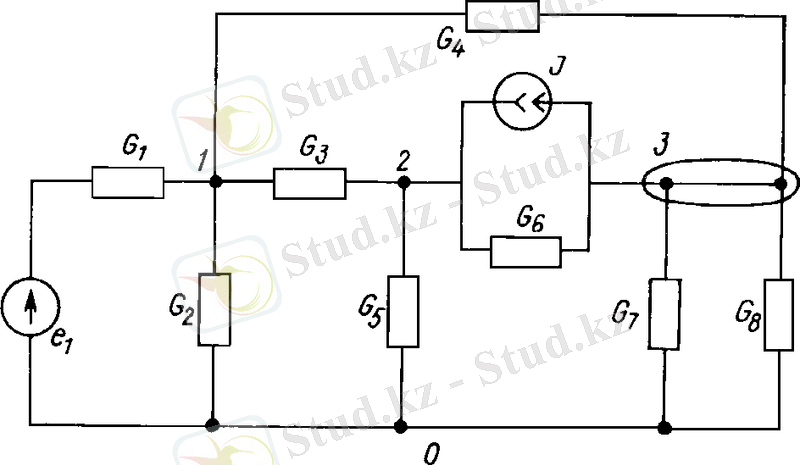
Суретте көрсетілген. 3. 2, түйіндерді нөмірлендіру түйіндердің ішкі және жалпы өткізгіштері үшін келесі өрнектерге әкеледі:

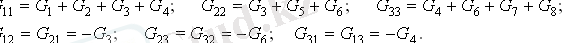
Түйіндік токтар бірдей J _1у = e ₁ G ₁ ; J _2у = J ; J _3у = - J .

Алынған өрнектер теңдеулер жүйесімен алмастырылады:. .

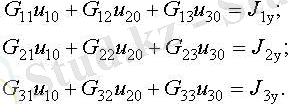
3. 4. NODE теңдеуін қалыптастыру кезіндегі БУХГАЛТЕРЛІК БАҚЫЛАУ КӨЗДЕРІ

Белсенді тізбектердің түйін теңдеулерін қалыптастыру тәртібі төмендегідей:

1) 3. 3-тармақта көрсетілген ережелерге сәйкес, бақыланатын көздерді тәуелсіз ретінде есепке ала отырып, тізбектің резистивті бөлігін қалыптастырамыз;

2) жүйенің оң жақ бөліктеріне түйіндік кернеулер арқылы кіретін осы көздердің бақылау ағымдары мен кернеулерін жедел басқару; Кирхгоф заңдары мен құрамдас теңдеулерді қолданамыз;

3) белгісіз түйін кернеулерін қамтитын түйін ағымдары үшін өрнектердегі терминдер теңдеулердің сол жағына ауысады және түйіндік өткізгіштердің матрицасының тиісті элементтерімен топтастырылады.

Жоғарыда көрсетілген қадамдардың орындалуын күрішке көрсетілген тізбектік фрагменттің үлгісімен көрсетейік. 3. 3.

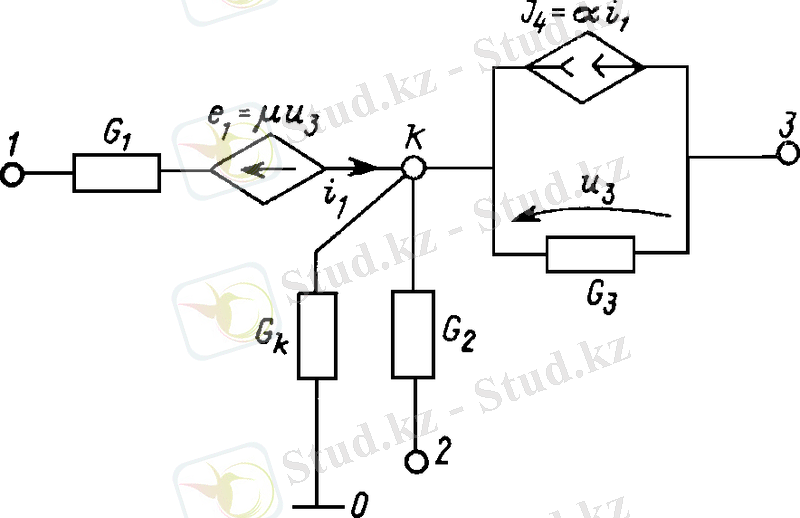
K-th торабы үшін түйін теңдеуінің бастапқы жазбасы, басқарылатын көздерді тәуелсіз ретінде ескере отырып, теңдеумен (3. 1)

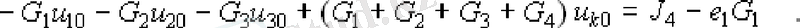
ЭМӨ және бақыланатын көздердің ағымы келесідей түйін кернеулері арқылы беріледі:

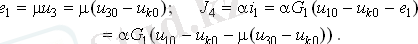
Осы сандарды түйіндік теңдеуге ауыстыру және терминдерді топтастыру, біз оны соңғы формаға дейін азайтамыз

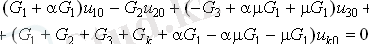
Нәтижесінде, белсенді тізбектің түйін теңдеулерінің матрицасы асимметриялық болып табылады - оның бірдей индекстерге тең емес диагональды элементтері бір-біріне тең емес. Бұл сипат белсенді тізбектердің түйін теңдеулері үшін тән.

Ұзартылған теңдестірілген теңдеулер

Басқарылатын көздердің ағымдары мен эмфдерін ескеретін терминдерді топтастыруға байланысты белсенді тізбектердің түйіндік теңдеулерінің алгебралық түрлендірулерін бұл ағымдарды және ЕМҚ-ны бірлескен шешілген теңдеулер жүйесіне қосымша белгісіз деп енгізуге болмайды. Бұл тiкелей мүдделер тізбегінің кейбір тармақтарында түйіндік теңдеулер мен ағымдар жүйесін шешу сатысында тікелей анықталған сандардың санын қосуға мүмкіндік береді. Жүйенің мұндай кеңеюден туындаған белгісіз санының өсуі заманауи есептеу техникасын пайдалану кезінде маңызды емес.

Мысалы, фрагменті суретте көрсетілген схемада болайық. 3. 1, ағымдағы i1 түйіндік теңдеулердің кеңейтілген жүйесінде қосымша белгісіз деп қарастырылады. Сонан соң, бірінші Кирхгоф заңының бастапқы теңдеуін (3. 1) өзгерткен кезде, біз бұл ағымды жоққа шығармаймыз. Нәтижесінде, ол пішінді қабылдайды

Осы токты түйіндік кернеумен байланыстырады

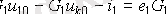
кеңейтілген жүйеге тәуелсіз теңдеу ретінде енгізілген.

E1 және J4 бақыланатын көздері бар белсенді тізбекті қарастырған кезде (3. 3-суретті қараңыз) біз қосымша белгісіз e1 және i1 кеңейтілген жүйені қалыптастырамыз. J4 = i1 қоспағанда және оның түйін теңдеуінің сол жақ бөлігіне өту соңғы береді

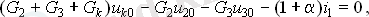
ал кеңейтілген жүйе енгізілген қосымша белгісіздерді e1 және i1 түйін кернеулерімен байланыстыратын қосымша теңдеулерді қамтиды:

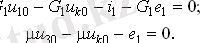
теңдеулер және оң жақ тараптардың коэффициенттерін кеңейтілген түйіндік жүйесін қалыптастыру кезінде токтар сипатталған өткізу филиалдары бар шарттарын қамтымайды. Қарастырылып жатқан мысалда бұл G1 филиалына жатады. филиалдардың токтар ол осы филиалы «плюс» бағыты кезде түйіннен ағымдағы және ағымдағы торабы бағытталған «минус» бар, қоса беріледі түйіндердің сол жағынан енгізілген. Қосымша теңдеулер ескере басқарылатын көздерін бақылау сомалары мен сипаттамалар арасындағы сілтемелер отырып, Кирхгоф заңдары негізінде құрылады жүйесін ұзартылды. Олардың саны кеңейтілген жүйеге енгізілген қосымша белгісіздер санына тең болуы керек.

3. 6. ЭДЕФ ҚҰРЫЛҒЫШЫ ЖӘНЕ ИДЕАЛДЫҚ КӨЗДЕРДІ ҚОЛДАНУШЫЛАРДЫҢ ҮНДІРІМДЕРІ ҮШІН НОД ЭЛЕМЕНТТЕРІН ҚҰРУ

Егер түйінге нөлдік ішкі кедергісі бар мінсіз EMF көздері бар вирустық бұтақтар қосылса, мұндай түйін үшін түйін теңдеуі оның мағынасын жоғалтады, өйткені нөлдік кедергіде филиалдың өткізгіштік шексіздікке тең.

Алайда, тәуелсіз икемді ЭМӨ көзі e байланысқан түйіндердің біреуі (3-суретті қараңыз, a) сілтеме (0) ретінде таңдалса, онда екінші түйіннің түйіннің кернеу мәні белгілі болады, себебі ол көзден тікелей анықталады: u10 = e.

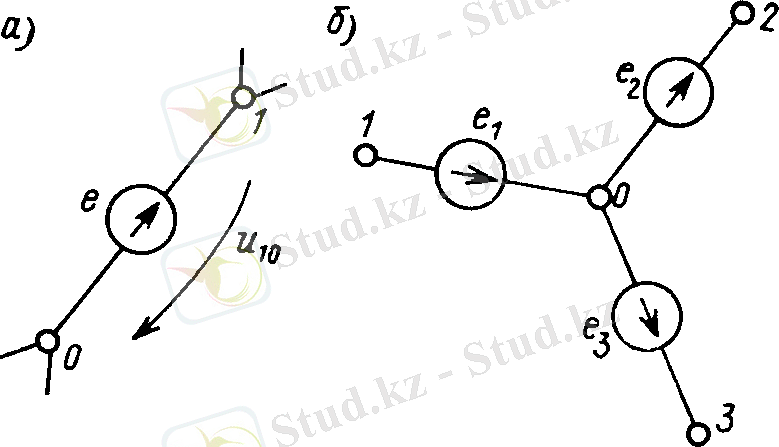
Осылайша, кәдімгі ережелер бойынша құрастырылған түйіндік теңдеулердің біреуі жоғалуы шешуге кедергі келтірмейді, өйткені белгісіз түйін кернеулерінің саны да сәйкесінше азаяды.

Сол сияқты, тізбектегі жалпы түйіндермен бірнеше идеалды көздердің әрекеті бойынша әрекет етеміз (3. 4-сурет, б) . Жалпы торап (0) ретінде таңдалған кезде, 1-ден 3-ке дейінгі түйіндер осы түйіндерге қосылған emf мәндерімен анықталады: u10 = - e1; u20 = e2; u30 = e3. Әлбетте, қарастырылып жатқан жағдайда, кез-келген түйіндерді (1, 2 немесе 3) анықтамалық түйін ретінде таңдауға болады. Қалған түйіндердің кернеулері идеалды көздердің эмфін алгебралық жинақтаумен анықталады. Нәтижесінде тізбектік кернеу әдісімен тізбекті есептеу үшін төменгі өлшемділік жүйесін аламыз.

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.