Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

Пән: Педагогика
Жұмыс түрі: Курстық жұмыс
Тегін: Антиплагиат
Көлемі: 28 бет
Таңдаулыға:

Қазақстан Республикасының білім және ғылым министрлігі

Ж. Досмұхамедов атындағы педагогикалық колледжі

КУРСТЫҚ ЖҰМЫС

Тақырыбы:

«Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары»

Орындаған:

Тексерген:

Орал, 2016ж.

Мазмұны

Кіріспе . . . 3

1. Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

1. 1 Квадрат теңдеулерді шешу жолының әр түрлі әдістері . . . 5

1. 2 Квадраттық теңдеу. Квадрат формуласы . . . 12

1. 3 Теңдік, теңсіздік, теңдеулер . . . 16

2. Квадрат теңдеулер тақырыбындағы сабақ жоспарлары

2. 1 Квадрат теңдеу түбірлерінің формулалары . . . 21

2. 2 Квадрат теңдеу. Квадрат теңдеудің түрлері . . . 23

Қорытынды . . . 26

Қолданылған әдебиеттер . . . 27

Кіріспе

Қазіргі заманның талаптарына сай еңбекке, қоршаған ортаға, қоғамға деген қарым - қатынастылықтар мен көзқарастарды қалыптастыру мектеп курсының барлық пәндерін оқыту процесінде жүргізіледі, орындалады. Алайда, осы бағытта математика пәнін алып қарастыратын болсақ, оның оқытудағы әдіс - тәсілді ерекшеліктеріне байланысты тәрбиелеуде өте қуатты құрал болып табылатынын сөзсіз.

Математиканың әр қадамы өмірдің қажетінен туады, сабақта қарастыратын көп есептер адамның практикалық дүниесіне байланысты. Сондықтан математикалық ұғымдардың нақты және тиімді болуы оқушылардың жеке тәрбиесіне байланысты, оқу жүйесіне қойыфлаын бірінші шарт - ол оқушылардың оқу процесі өмірімен байланысты болуы. Математикадан алған білім, біліктерін оқушылар тек еңбек және оқу әрекеттерінде қолданып қоймай, сонымен қатар мәдениеттің басқа салаларын да меңгертуге де пайдалануға болады. Математиканың тәрбиелік әсер етуі - оқушылардың бойында ой - өрісті, саналы ойлай білу ерекшеліктерін, өмірге деген көзқарастарын, танымдық ерекшеліктерін, патриоттылық сезімдерін оята отырып дамыту, қалыптастыруда үлкен роль атқарады. Ал, ондай жетістіктерге алгебралық материалдарды жетік меңгеру арқылы жеткізу мүмкін .

Білім өркениеттіліктің әрі өлшемі, әрі тетігі болып табылатындықтан кез келген мемлекеттің рухани және әлеуметтік дәрежесі білім деңгейіне байланысты бағаланады.

Жан-жақты үйлесімді, өркениетті елдің ұрпағын тәрбиелеп шығу бүгінгі мектептің алдына қойылған мақсаттардың бірі. Бұл мақсат әрбір орта мектеп мұғалімінен бүгінгі заман талабына сай оқыту әдістемесін күннен күнге жетілдіре түсуін талап етеді. Осы талаптың орындалуы орта мектеп бағдарламасындағы әрбір пәннің әр тарауының әр тақырыбын оқушы санасына жететіндей етіп оқытқанда ғана орындалады. Олай болса, оқушыларды жеке тұлға етіп тәрбиелеуде математика пәнінің де алатын орны, салмағы зор.

Бұл мақала алгебра курсында қарастырылатын квадрат теңдеулерге және оларды шешу жолдарының әр түрлі әдістеріне негізделініп отыр.

«Квадрат теңдеулер» мектептегі алгебра курсының маңызды тақырыптарының бірі. Көптеген табиғи үдірістер мен құбылыстар, с. с. мазмұнды есептердің шығарылуы квадрат теңдеулерді шешуге келіп тіреледі. Теңсіздіктерді шешу, функцияларды зерттеу (функцияның нөлдерін, экстремум нүктелерін, өсу және кему аралықтарын табу), ең үлкен және ең кіші мәндерді табу есептерін шығару және т. б. жағдайларда квадрат теңдеулерді шеше білу қажеттігі туындайды. Сондай-ақ тригонометриялық, көрсеткіштік және логарифмдік теңдеулерді, физикада және техникада, геометрия курсының есептерін алмастыру тәсілімен шешкенде квадрат теңдеулерге келтіріледі.

1. Мектеп математикасындағы квадраттық теңдеулерді шешу жолдары

1. 1 Квадрат теңдеулерді шешу жолының әр түрлі әдістері

«Квадрат теңдеулерді» шешу жолдарының тоғыз түрлі әдісі бар. Атап айтқанда, олар төмендегідей болып табылады:

1-әдіс. Теңдеудің сол жақ бөлігін көбейткіштерге жіктеу

Мысал: х ² +4х+3 =0 теңдеуін шешейік.

Теңдеудің сол жақ бөлігін көбейткіштерге жіктейміз:

х ² +х+3х+3 =х(х+1) +3 (х+1) =(х+1) (х+3)

Демек, теңдеуді былай жазуға болады: (х+1) (х+3) =0

Көбейтінді нөлге тең болғандықтан, ең болмағанда көбейткіштердің біреуі нөлге тең болуы керек. Сондықтан теңдеулердің сол жақ бөлігіндегі х 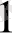=-1 және сандары х ² +4х+3=0 теңдеуінің түбірлері болып табылады.

2-әдіс. Толық квадратқа келтіру әдісі

Мысал: х ² +8х-9=0 теңдеуін шешейік.

Сол жақ бөлігін толық квадратқа келтіреміз. Ол үшін х ² +8х өрнегін төмендегідей жазып аламыз: х ² + 8х=х ² +2х4

Алынған өрнектің бірінші қосындысы х-тың квадраты, ал екінші қосындысы х пен 4-тің екі еселенгені. Толық квадрат алу үшін 4 ² -ын қосу керек. Сонда х ² +2х4+4 ² =(х+4) ²

Енді теңдеудің сол жағын түрлендіреміз. Берілген теңдеуге 4 ² -ын қосып, алып тастаймыз. Сонда шығатыны: х ² +8х-9=х ² +2х4+4 ² -9-4 =(х+4) ² -25

Сонымен, берілген теңдеуді былайша жазуға болады: (х+4) ² -25=0, яғни (х+4) ² =25.

Бұдан х+4=5, х 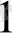=1 немесе х+4=-5, х 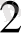= -9. Жауабы: 1; -9

3-әдіс. Квадраттық теңдеулерді формула арқылы шешу

ах ² +вх+с=0, а≠0 теңдеудің екі жағын да 4а-ға көбейтеміз де, төмендегі өрнекті аламыз:

4а ² х ² +4ахв+4ас=0

((2ах) ² +4ахв+в ² ) -в ² +4ас=0, (2ах+в) ² =в ² -4ас

2ах+в= Equation. 3 , 2ах = -в

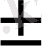
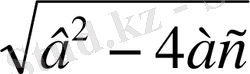
х = (1)

Оған келесідегідей мысалдар келтіруге болады:

1) 3х ² -7х+4=0 теңдеуін шешейік.

а=3, в=-7, с=4. Д=в ² -4ас=(-7) ² -4·4·3=49-48=1.

Д>0 болғандықтан, екі әр түрлі түбір болады: х ₁ =1, х ₂ =

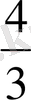
Сонымен, дискриминант оң болғанда, яғни в ² -4ас>0, ах ² +вх+с=0 теңдеуінің екі түрлі түбірі болады.

2) 9х ² +6х+1=0 теңдеуін шешейік.

а=9, в=6, с=1. Д=в ² -4ас=6 ² -4·9·1=0.

Д=0 болғандықтан, бір ғана түбір бар болады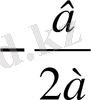: х= , х=

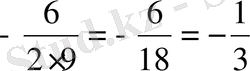
Сонымен, егер дискриминант нөлге тең болса, яғни в ² -4ас=0, ах ² +вх+с=0 теңдеуінің жалғыз

түбірі бар болады: х=

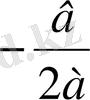
3) х ² +2х+3=0 теңдеуін шешейік.

а=1, в=2, с=3. Д=в ² -4ас=4-4·3·1= -8.

Д<0 болғандықтан, теңдеудің нақты сандар өрісінде түбірі болмайды.

Сонымен, егер дискриминант теріс болса, яғни в ² -4ас<0, онда ах ² +вх+с=0 теңдеуінің түбірі болмайды.

4-әдіс. Виет теоремасын пайдаланып теңдеулерді шешу

Келтірілген түбірлері Виет теоремасын қанағаттандырады.

Ол былай беріледі: а=1 болғанда,

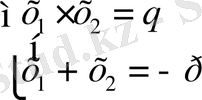
Бұдан келесі тұжырымдарды шығаруға болады:

а) Егер q (1) теңдеудің бос мүшесі оң болса (q 0) онда теңдеудің екі бірдей таңбалы түбірі болады. Егер р>0, онда екі түбірі де теріс болады, егер р<0, онда түбірлері оң болады.

Мысал, 1) х ² -9х+20=0, х ₁ =4, х ₂ =5, мұнда q=20 >0, р=-9 <0;

2) х ² +5х+6 =0, х ₁ =-2, х ₂ =-3, мұнда q =6 >0, р =5 >0.

б) Егер q (1) теңдеудің бос мүшесі теріс болса (q <0), онда теңдеудің екі түрлі, таңбалы екі түбірі болады, түбірдің модулі бойынша үлкені оң болады, егер р <0 болса, теріс болады, егер р >0. Мысал, 1) х ² +3х-4 =0; х ₁ =-4, х ₂ =1 мұнда q =-4 <0, р=-3 >0

2) х ² -7х-8 =0; х ₁ =8, х ₂ =-1 мұнда q =-8 <0, р =-7 <0

5-әдіс. Теңдеуді «асыра лақтыру» әдісімен шешу

ах ² +вх+с =0, а ≠0 квадрат теңдеуін қарастырамыз. Теңдеудің екі жағын да а-ға көбейтіп, мынаны аламыз: а ² х ² +авх+ас=0. ах =у деп белгілесек, х = 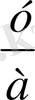. Олай болса у ² +ву+ас =0 теңдеуіне келеміз. Бұл бастапқы теңдеумен тең. Теңдеудің түбірлерін у ₁ , у ₂ -ні Виет теоремасы арқылы табамыз. Соңында х ₁ = 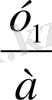, х ₂ = 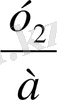-ны аламыз. Бұл жағдайда

а коэффициентін бос мүшеге көбейтеді. Сондықтан да бұл әдісті «асыра лақтыру» әдісі деп атайды [1, 13бет] . Бұл әдісті көбінесе Виет теоремасын пайдаланып түбірді оңай табуда және дискриминант дәл квадрат болғанда қолданады.

Мысал: 2х ² -9х+9=0 теңдеуін шешейік.

Шешуі: 2 коэффициенті теңдеудің бос мүшесіне асыра лақтырамыз, нәтижесінде

у ² -9у+18=0 теңдеуін аламыз. Виет теоремасы бойынша

Жауабы: 3; 1, 5.

6-әдіс. Квадрат теңдеулердің коэффициенттерінің қасиеттерін қолдану

ах ² +вх+с=0, а≠0 квадрат теңдеуі берілген.

Егер а+в+с=0 (яғни коэффициенттер қосындысы 0-ге тең) болса, онда х ₁ =1, х ₂ =

Мысал: 7+2-9=0 қосындысы 0-ге тең. Осы үш сан үшін квадрат теңдеу құрастырып, оны шешейік:

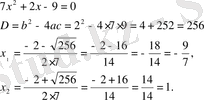
7-әдіс. Квадрат теңдеуді циркуль және сызғыш көмегімен шешу

ах ² +вх+с=0 квадраттық теңдеуін циркуль және сызғыш көмегімен шешу әдісін ұсынамыз (1-сурет) . Ізделінді шеңбер абцисса өсінде В(х ; 0) және Д (х ₂ ; 0) нүктелерінде қиылыссын делік. Мұндағы х ₁ , х ₂ - ах ² + вх + с=0 теңдеуінің түбірлері және ординат осінен А(0; 1) және С(0; ) нүктелері арқылы өтеді делік. Олай болса, қима туралы теорема бойынша мынаны аламыз:

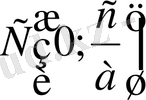
ОВ·ОД=ОА·ОС,

бұдан ОС=

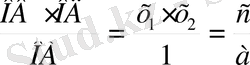
1-сурет

Шеңбер центрі АС және ВД хорда ортасында орналасқан перпендикуляр SF пен SК-ның

қиылысу нүктелері болып табылады, сондықтан SК= ;

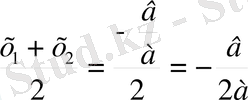SF =

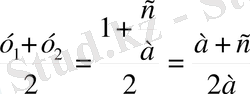
Сонымен,

1) S 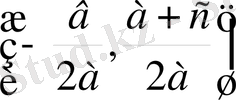(шеңбер центрі) және А (0; 1) нүктелерін тұрғызамыз;

2) SА радиусты шеңбер жүргіземіз;

3) Осы шеңбердің Ох осі арқылы өтетін қиылысу нүктелері бастапқы квадрат теңдеудің түбірі болады.

Сонымен үш түрлі жағдай болуы мүмкін:

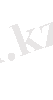
1-ші жағдай. Шеңбер радиусы ордината центрінен артық (АS > SК, немесе, 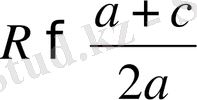шеңбер Ох осін екі нүктеде (2а-сурет) В (х ; 0) және Д (х ₂ ; 0) нүктелерде қияды. Мұндағы х ₁ және х ₂ -ах ² +вх+с =0 квадрат теңдеуінің түбірлері) .

2-ші жағдай. Шеңбер радиусы ордината центрінде (АS= SК; немесе 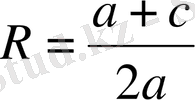тең, шеңбер Ох осін В (х ₁ ; 0) нүктесінде (2б) -сурет) жанап өтеді, мұндағы х ₁ - квадрат теңдеудің түбірі) .

3-ші жағдай. Шеңбер радиусы ордината центрінен кіші (А S < SК, немесе 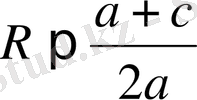) кем, щеңбердің абцисса осімен қиылысатын нүктесі жоқ (2в - сурет), бұл жағдайда теңдеудің шешімі болмайды.

у у у

2-сурет

а) АS>SВ, 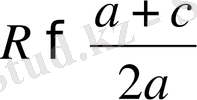екі шешімі бар: х ₁ және х ₂

б) АS=SВ, 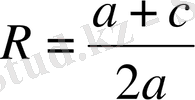бір шешімі бар: х ₁

в) АS<SВ, 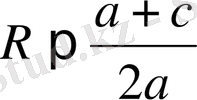шешім жоқ.

8-әдіс. Квадрат теңдеуді номограмма көмегімен шешу

O B E y 3

F D

y y 3y

H A

3-сурет 4- сурет

Бұл квадрат теңдеуді шешудің бұрынғы және жөнсіз ұмыт болған әдісі.

Брадис таблицасында z ² +pz+q=0 теңдеуін шешуге арналған номограмманы қарастырайық. Бұл номограмма квадрат теңдеудідің түбірлерін анықтауға мүмкіндік береді. Номограмманың қисық сызықты шкаласы төменгі формулалар бойынша тұрғызылған (жоғарыдағы 3-суретте бейнеленген) .

ОВ= 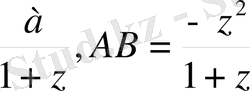ОС=р, ЕД=q, ОЕ=а десек, мұндағы САН және СДF үшбұрыштарының ұқсастығына мынадай пропорция аламыз:

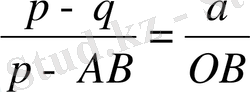Мұнда z ² +pz+q=0 теңдеуді ауыстыру жасағаннан және жеңілдеткеннен шығады, бұл жердегі z әрпі қисық сызықты шкала нүктесінің кез-келген белгісін білдіреді.

9-әдіс. Квадрат теңдеулерді геометриялық әдіспен шешу

Көне заманда алгебраға қарағанда геометрия көбірек жетілген кезде, квадрат теңдеулерді алгебралық жолмен емес геометриялық жолмен шеше білген. Ежелгі гректер мына у ² + 6у-16=0 теңдеуін қалай шешкендігіне тоқталып өтейік.

Шешуі: жоғарыдағы 4-суретте көрсетілген, мұндағы у ² +6у=16 немесе у ² +6у+9=16+9

у ² +6у+9 және 16+9 өрнекті геометриялық тұрғыда сол квадраттың өзін береді, ал

у ² +6у-16+9-9=0 бастапқы теңдеу де сол теңдеу. Бұдан алатынымыз у+3= 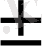5 немесе у ₁ =2, у ₂ =-8.

Мақалада қарастырылған 9 әдіс те оқушылардың «Квадрат теңдеулер» тақырыбын терең меңгеруіне жол ашады. Сонымен қоса, квадрат теңдеулерді шешудің барлық тоғыз әдісі де қолданыс тапқанда оқушылардың пәнге деген қызығушылығы мен логикалық ойлау қабілеті артады.

1. 2 Квадраттық теңдеу. Квадрат формуласы

2-дәрежелі көпмүше немесе квадраттық теңдеу, квадраттық үшмүшелік деп

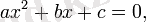
түріндегі көпмүшелі теңдеуді айтамыз. Мұндағы a≠0 (Егер a = 0 болса, теңдеу ) . Квадрат теңдеудің графигі - парабола (яғни квадрат функция) . Квадрат теңдеу - 2-дәрежелі алгебралық теңдеу. Оның жалпы түрі мынадай: ax2+bx+c=0, a≠0. Квадрат үшмүше комплекс сандар жиынында 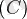сызықтық көбейткіштерге жіктеледі: 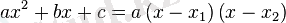, мұндағы 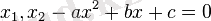квадрат тендеудің түбірлері; 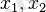- сандарыквадрат үшмүшенің түбірлері деп те, сонымен қатар бұлар 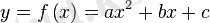квадрат функциясының нөлдері деп те аталады. Квадрат үшмүшені мына түрде де жазуға болады:

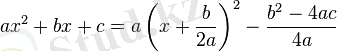
Осы өрнек нақты айнымалының квадрат функциясының графигін салу кезінде функцияның ең үлкен ( 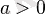болғанда) немесе ең кіші ( 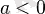болғанда) мәндерін анықтау үшін пайдаланылады. 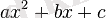квадрат функциясының графигі парабола болады, оның 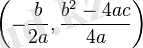нүктесінде орналасқан.

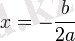-- түзуі параболаның симметрия осі болып табылады. 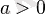болғанда параболаның тармақтары жоғары карай, 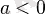болғанда - төмен қарай бағытталады. 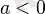болғанда 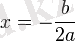нүктесінде максимумға кетерілсе, ал 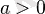болғанда 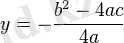нүктесінде минимумға төмендейді.

Парабола ордината осін ( 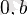) нүктелерінде қиып өтеді. Егер квадрат үшмүшенің нақтытүбірлері 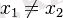болса, онда парабола абсцисса осін 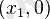және 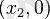нүктелерінде қиып өтеді, болса, парабола абсцисса осімен 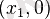нүктесінде жанасады. [1]

a, b, және c әріптері - коэффиценттер деп аталады: a квадраттық коэффиценті - x2-тың коэффиценті, b коэффиценті - x-тің коэффиценті, ал c - тұрақты коэффицент немесе тұрақты мүше.

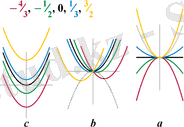
ax2 + bx + c - ның графиктері (Әр коэффицентінің мәнін өзгерткенде)

Квадрат формуласы

Квадрат теңдеудің коэффиценттері нақты болса, оның екі шешімі немесе түбірі болады. Оларды квадрат формуласы сипаттайды:

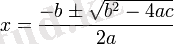яғни:

және: және

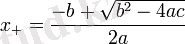
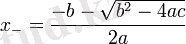
Дискриминант

Дискриминант мәндеріне байланысты түбірлер
- <0: x2+1⁄2
- =0: −4⁄3x2+4⁄3x−1⁄3
- >0: 3⁄2x2+1⁄2x−4⁄3

Төмендегі формула квадрат түбірлерді табуға қажет:

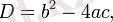
Бұл дискриминант деп аталады.

Квадрат функцияның коэффиценттері нақты сан болса (комплекс сан емес) онда оның бір әлде екі нақты немесе екі комплекс түбірлері бар. Осыған байланысты дискриминант түбірлердің түрі мен санын анықтайды. Дискриминант мәніне байланысты үш жағдай болуы мүмкін:

Егер дискриминант оң сан болса теңдеудің 2 түбірі бар және олар нақты:

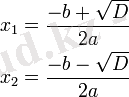
Егер дискриминант нөлге тең болса, теңдеудің бір нақты түбірі бар:

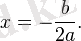
Егер дискриминант теріс сан болса теңдеудің нақты түбірлері жоқ. Керісінше, теңдеудің екі комплекс түбірі бар:

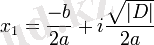мұнда 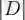- абсолют мәні(+ve) және =

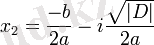
Виет формуласы

x2+px+q=0 түріндегі келтірілген квадрат теңдеудің шешімі төмендегіше өрнектеледі: x1, 2=. Квадрат теңдеудің түбірлері мен коэффициенттері бір-бірімен мынадай қатынастар арқылы байланысқан: x1+x2=, x1x2= .

Мысалдар

теңдеуінде дискриминант оң: 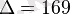және екі нақты шешімі (түбірлері) бар:

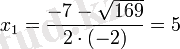
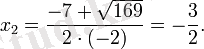
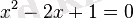теңдеуінің дискриминанты нөлге тең: =0 яғни, теңдеудің бір шешімі бар:

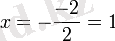
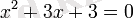теңдеуінің нақты сандар арасында шешімі жоқ, өйткені: . Бірақ екі комплекс түбірлері бар:

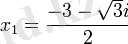
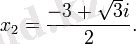
Квадрат теңдеудің сол жақ бөлігін (x-x2) =0⋅a(x-x1) түрінде көрсетуге болады. ге келтірілетін есептерді шешу мәселесі ежелгі дәуір математиктеріне де белгілі болған. Квадрат теңдеу терминін неміс философы әрі математигі Х. Вольф (1679 - 1754) енгізген.

1. 3 Теңдік, теңсіздік, теңдеулер

Теңдік теңсіздік және теңдеулер туралы ұғым олардың өзара байланысы тұрғысында айқындалады. Олармен жұмыс І кластан бастап арифметикалық материалды оқу мен тығыз байланыста жүргізіледі. Сандық теңдіктер және теңсіздіктер

Балаларды сандарды салыстыруға үйрету, сондай-ақ «артық», «кем», «тең» қатынастарын тағайындау мақсатында өрнектерді салыстыру; “>”, “<”, “=”, таңбаларының көмегімен салыстыру нәтижелерін жазуға және алынған теңдіктер мен теңсіздіктерді оқуға үйрету мақсаты қойылады.

Сандық теңдіктер мен теңсіздіктерді оқушылар берілген сандар мен арифметикалық өрнектерді салыстыру негізінде алады. Сондықтан “>”, “<”, “= ”, таңбалары арқылы кез келген екі сан, кез келген екі өрнек қосылмайды, тек арасында белгілі қатынас бар сандар ғана қосылады. Мәндер тең, “=” таңбасы арқылы берілген екі сан немесе екі өрнек теңдік құрады.

Егер бір сан екінші саннан артық (кем) немесе бір өрнек екінші өрнектен артық (кем) болса онда сәйкес таңбамен қосылған олар теңсіздік құрады. Сонымен алғашқыда төменгі класс оқушыларында тек тура теңдік пен теңсіздік туралы ұғым қалыптасады.

Кейін, оқушылар өрнектермен және айнымалысы бар теңсіздіктермен жұмыс істеу тәжірибесін жинақтағанда, ақиқат және жалған (тура және тура емес) пікірлер ұғымын қарастырғаннан кейін IV класта теңдік пен теңсіздік ұғымының мынадай анықтамасына көшеді, ол анықтама бойынша “=” таңбасы қойылған кез келегн екі сан, екі өрнек теңдік деп аталады; “>”, “<” таңбаларының біреуі арқылы біріктірілген кез келген екі сан., екі өрнек теңсіздік деп аталады. Мұнда тура және тура емес теңдік пен теңсіздіктің айырмасын атап айтады.

Ұғымдарды айқындаудың мұндай жолы ілгеріде айқындала түсетін теңдіктермен, теңсіздіктермен және теңдеулермен жұмыс істеу методикасын анықтайды.

Бастауыш кластарда теңдікпен және теңсіздікпен таныстыру нумерацияны және арифметикалық амалдарды оқып үйренумен байланыстырылады.

Сандарды салыстыру әуелі өзара бір мәнді сәйкестікті тағайындау арқылы орындалатын жиындарды салыстыру негізінде іске асырылады. Жол жөнекей жиындар элементтерін санау және алынған сандарды салыстыру жұмысы орындалады (дөңгелектер 7, үшбұрыштар 5, үшбұрыштардан дөңгелектер артық, 7 саны 5 санынан артық) . Алдағы уақытта сандарды салыстырғанда оқушылар олардың натурал катардағы орнына сүйенеді. 9 саны 10-нан кем, өйткені санаған кезде 9 санын 10 санынан бұрын атайды; 5 саны 4-тен артық, себебі санау кезінде 5 санын 4 санынан кейін атайды.

Тағайындалған қатынастар “>”, “<”, “=”, таңбаларының көмегімен жазылады, оқушылар теңдіктер мен теңсіздіктерді оқуға және жазуға жаттығады.

100, 1000 көлеміндегі сандар нумерациясын, сондай-ақ көп таңбалы сандар нумерациясын оқып үйренгенде сандарды салыстыру, ол сандарды не олардың натурал қатардағы орны бойынша немесе сандардың ондық құрамы бойынша жіктеу және жоғары разрядтан бастап сәйкес разрядтық сандарды салыстыру негізінде іске асырылады (75>48, себебі 7 ондық 4 ондықтан артық, 75<73, себебі ондықтары тең, ал бірліктері бірінші санда екінші сандағыдан артық) .

Атаулы сандарды салыстыру әуелі шамалардың мәндерінің өздерін салыстыруға сүйенеді, содан кейін дерексіз сандарды негізінде іске асырылады, ол үшін берілген атаулы сандар бірдей өлшеу бірліктерімен өрнектеледі. Атаулы сандарды салыстыру оқушыларға үлкен қиыншылық келтіреді, сондықтан бұл операцияға үйрету үшін І-ІІІ кластарда үнемі әр түрлі жаттығуларды ұсынады, мысалы:

1) Мыналарды бірдей болатындай етіп сандарды таңдап алыңдар. 7 км 500м =м, 3080кг = т кг.

2) Жазуы дұрыс болатындай етіа сандарды таңдап алыңдар: сағ < мин, см, т ц =кг

3) Жазу дұрыс болатындай етіп сандардың атауларын қойыңдар. 35 км = 35 000… .

4) Берілген теңдік тура немесе тура еместігін ( сол жағындағы

сандарды, оң жағындағы сандарды) тексеріп көріңдер, егер теңдіктер тура болса, онда: 4 т 8ц =480 кг, 100 мин=1 сағ 2м 5см =250 см.

Осы сияқты жаттығулар балаларға олардың тең және тең емес атаулы сандар ұғымын ғана меңгеруге көмектесіп қоймай, сонымен қатар өлшеу бірліктерінің таблицасын қатар өлшеу бірліктерінің таблицасын меңгеруге де көмектеседі.

Өрнектерді салыстыруға көшу біртіндеп іске асырылады. Әуелі 10 көлемінде қосу және азайтуды оқып үйренгенде балалар ұзақ уақыт бойы өрнек пен санды (сан мен өрнекті) салыстыруға жаттығады. 3+1>3, -1<3 түріндегі бірінші теңсіздіктерді (3=3) теңдігінен алған пайдалы, мұнда түрлендіруде жиындарға қолданылатын сәйкес операцияларды қолдану керек. Мысалы, кластың қалталы полотносына және парта үстіне 3 үшбұрыш және 3 дөңгелек қойып, оған 3=3 деп жазылған. Оқытушы балалрға 3 үшбұрышқа тағы 1 үшбұрыш қосып, оны жазуды ұсынады (3+1- үшбұрыш астындағы жазу) . Дөңгелектер саны азаймаған (3) . Оқушылар үшбұрыштар мен дөңгелектер санын салыстырып, дөңгелектерге қарағанда үшбұрыштар саны көп (4>3) екндігіне көздерін жеткізеді, демек, 3+1>3 деп жазуға болады (үш қосу бір үштен артық) . Осындай жұмыс 3-1<3 теңсіздігімен де жүргізіледі.

2. Квадрат теңдеулер тақырыбындағы сабақ жоспарлары

2. 1 Квадрат теңдеу түбірлерінің формулалары

Сабақтың тақырыбы : Квадрат теңдеу түбірлерінің формулалары

Сабақтың түрі: Ой жарыс, білім сайыс сабағы.

Сабақтың типі : Аралас сабақ

Әдіс-тәсілі: Ұжымдық, топтық оқыту.

Сабақтың мақсаты : оқушылардың теңдеулерді шешу тақырыбы бойынша алған білімдерін жүйелеу.

Біліктілік: Квадраттық теңдеулерді формула көмегімен шығаруды үйрету, толымсыз квадраттық теңдеулер туралы алған білімдерін бекіту

Дамытушылық: Оқушылардың ақыл-ойын дамыту, ойлау қабілетін жетілдіру, есеп шығарудың жаңа түрлерін меңгерту және ойдан ой туындатуға, әр сөзді, айтылған ойды дәлелдеуге үйрету

Тәрбиелік: Есеп шешімін іздеу арқылы қиыншылықты жеңуге, ұйымшылдыққа, дербестікке, дәлдікке тәрбиелеу.

Сабақтың көрнекілігі : интереактивті тақта, тапсырмалар жазылған карташалар (слайдтар) .

Са бақтың барысы :

Ұйымдастыру Барлығы 25 ұпай

Үй жұмысын тексеру «Блиц сұрақтар» 5 ұпай

Өзіңді тексер. Жеке жұмыс 5 ұпай

Оқулықпен жұмыс 5 ұпай

«Зерек» ойыны әрбір есеп 3 ұпай

Қосымша формулалар 3ұпай

Топпен жұмыс 5 ұпай

... жалғасы

Сіз бұл жұмысты біздің қосымшамыз арқылы толығымен тегін көре аласыз.