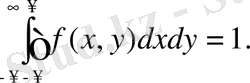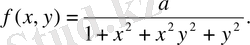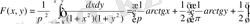Зертханалық жұмыс №5: Кездейсоқ сигналдардың таралу заңдары мен статистикалық сипаттамалары


№5 Зертқаналық жұмыс
Кесдейсоқ сигналдардың таратушы заңдарын зерттеу
Жұмыстың мақсаты: кездейсоқ процесстерді лездік мәндердің ықтималдық тығыздықтарын тәжірибелік зерттеудің әдістемесімен танысу. Кездейсоқ процесстің сипатымен, оның сандық сипаттамаларымен және ықтималдық тығыздық граыиктерімен есептік байланыстарын алу.
Құрал жабдықтар: лабораториялық стенд
Бақылау сұрақтары
- Кез келген сигналдың ықтималдық тығыздықтың графигін салыңыз. Остер өлшемдер бойымен бөліп шығаруын түсіндіріңіз. «Ықтималдық тығыздық» ұғымының мағынасы.
- Ықтималдық тығыздықты қалай іс жүзінде табады?
- Қалыпты кездейсоқ процесс деген не? Оның аналитикалық жазбасын көрсетіңіз.
- Қалыпты заң үшінW(x) кестесінσ\sigmaжәнеmоның және көбею не кішірею өзгерісін салыңыз.
- Қалыпты заңдыW(x) график бойымен математикалық күтімді және дисперцияны қалай табамыз?
- БерілгенΔ\mathrm{\Delta}xаралықтың дәл келуінің ықтималдығын қалай анықтаймыз?
- ықтималдық тығыздықтың графигі бойымен;
- үлестіру функциясының графигі бойымен;
- Байланыс сигналдарына қарай математикалық күтім мен дисперция ұғымдарының физикалық мағынасын түсіндіріңіз.
- Тұрақты және тұрақты емес процесстердің айырмашылығы неде?
- Эргодиялық процесс дегеніміз не?
- Кездейсоқ процесс және оның өткізуі дегеніміз не?
1. Егер X пен Ү үздіксіз кездейсоқ шамалар болса, онда олардың біріккен ықтималдық тығыздығы
(1)
теңдігімен анықталады.
(1) тендіктің оң жағын үлестірім функциясы арқылы
өрнектесек
(2)
Егер үлестірім функциясы Ғ(х, у) және оның екінші ретті туындысы үздіксіз болса, онда (2) теңдіктің оң жағы F(х, у) функциясының аралас туындысын береді:
(3)
Сонымен екі кездейсоқ шамалар системасының ықтималдық тығыздығы кездейсоқ (Х, Ү) нүктесінің элементар тік төрбұрыш ауданына түсу ықтималдығының сол ауданға қатынасының шегіне тең
(
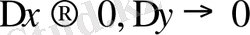 ) Үлестірім тығыздығын үлестірім функциясының екінші ретті аралас туындысы арқылы есептеуге болады
f
(х, у) функциясының графигін үлестірім беті деп атайды.
) Үлестірім тығыздығын үлестірім функциясының екінші ретті аралас туындысы арқылы есептеуге болады
f
(х, у) функциясының графигін үлестірім беті деп атайды.
Екі кездейсоқ шамалар системасы үшін f (х, у) dxdy көбейтіндісі ықтималдық элементі деп аталып, ол өлшемдері dх жөне dу болатын тік төрбұрышқа кездейсоқ нүктенің түсу ықтималдығын көрсетеді.
Ықтималдық элементінің геометриялық мағынасы: табаны dх және dу болатын тік төртбұрыш, ал биіктігі f (х, у) -ке тең элементар параллелепипедтің көлемін береді (1-сурет) .
1-сурет
Сонымен, үлестірім тығыздығы f (х, у) болса, кездейсоқ (Х, Ү) нүктесінің берілген В облысына түсу ықтималдығын келесі формуламен анықтауға болады:
(4)
Үлестірім функциясы Р(х, у) абциссалары (-
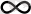 , х) және ординаталары (-
, х) және ординаталары (-
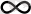 , у) аралығындағы квадрантқа түсу ықтималдығын көрсететін болғандықтан оны ықтималдық тығыздығы
f
(х, у) арқылы былай өрнектейді:
, у) аралығындағы квадрантқа түсу ықтималдығын көрсететін болғандықтан оны ықтималдық тығыздығы
f
(х, у) арқылы былай өрнектейді:
(5)
Екі кездейсоқ шамалар системасының ықтималдық
тығыздығының қасиеттерін қарастырайық.
1°. Ықтималдық тығыздығы теріс емес мәндерді қабылдайтын функция: f(x, y)
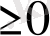 .
.
(1) тендік бойынша бөлшектің алымы мен бөлімі оң мәндер қабылдайды, ал оның шегі теріс болуы мүмкін емес.
2º. Ықтималдық тығыздағынан алынған қос меншіксіз интеграл мәні бірге тең
Үлестірім функциясының қасиеті бойынша F(
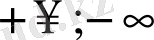 ) болғандықтан (5) формула негізінде:
) болғандықтан (5) формула негізінде:
.
Бұл теңдіктің геометриялық мағынасы үлестірім беті мен жазықтығы арқылы шектелген дененің көлемі бірге тең болады.
Мысалы. Екі кездейсоқ шамалар системасының ықтималдық тығыздығы
а
параметрінің мәнін, үлестірім функциясын
f
(x, y) және кездейсоқ нүктенің төбелері О(0, 0), А(0, 1), В(
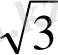 , 1), С(
, 1), С(
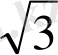 , 0) нүктелерінде болатын тік төртбұрышқа түсу ықтималдығын табу керек.
, 0) нүктелерінде болатын тік төртбұрышқа түсу ықтималдығын табу керек.
Шешуі. Ықтималдық тығыздығының екінші қасиеті бойынша а параметрінің мәні:

Осыдан
a
=
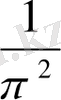 .
.
Үлестірім функциясын F(x, y) (5) формуламен анықтаймыз:
Кездейсоқ (X, Y) нүктесінің берілген D облысына түсу ықтималдығы (4) формула арқылы табамыз:
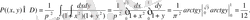
2. Ықтималдық P i деп: физикалық шамалардың өлшенген мəндерінің N i санының, ансамблдегі барлық элементтердің санына N қатынасының шегін (ансамблдегі элементтің саны шексіздікке өскен кездегі) айтамыз:
(6)
Бұл формуланы эвивалентті түрде жазуға болады:
(7)
мұндағы t i - жүйе i күйінде (x ξ, i мəні) болған кездегі уақыт, T- бақылаудың толық уақыты . Бұл формулалар (6), (7) системаның сыртқы шарттары өзгеріссіз күйде болған кезде орындалады.
Үздіксіз кездейсоқ сигналдар үшін ықтималдылықтың (6), (7) анықтамасын дəлірек алу қажет. Себебі, үздіксіз шамалар шексіз (есепсіз мəндер) мəндердің жиынын қабылдайды, сондықтан t i уақыты нөлге тең болғандықтан P i де нөлге тең болады. Осы себепті кездейсоқ шаманың болатын мəндерінің белгілі интервалын қарастыру керек, мысалы 0< x ξ <. x. Сонда біз дискретті жағдаймен ұқсастыққа келеміз жəне үздіксіз кездейсоқ шама x(t) үшін ықтималдылықтың таралу функциясының анықтамасын (ықтималдылықтың таралу заңдылығының аналитикалық өрнегін) сипаттай аламыз:
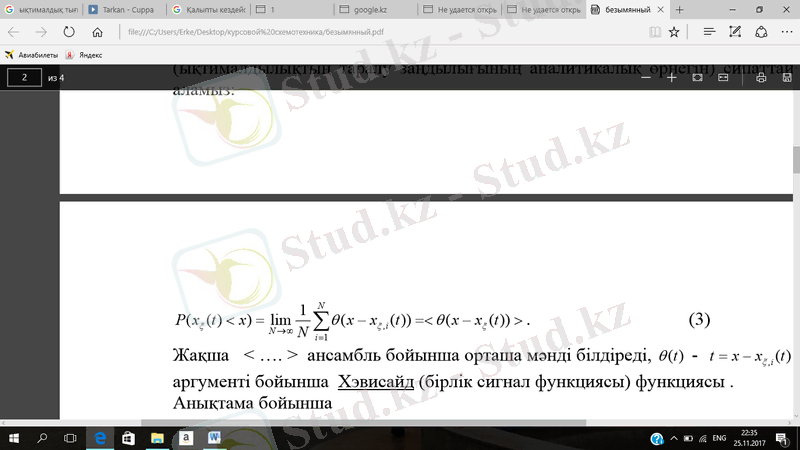
3. Уақыт бойынша өзгеретін кездейсоқ сигналдың математикалық моделі кездейсоқ процесс деп аталады. Егер ξ(t) - кездейсоқ сандардың тізбегі (кездейсоқ күш) болса, функцияның ерекше түрін - онда кездейсоқ процесті x ξ (t) түрінде белгілейміз. Табиғи жағдайда кездейсоқ күштердің ξ i (t ) (i=1, 2, …N) тізбегі кездеседі, оған x i, ξ (t) ансамблі сəйкес келеді. Ансамбілдің сигналдың қабылдануынан кейін толық белгілі болған осы функциялардың бірі кездейсоқ процестің байқалуы деп аталады. Бұл байқалуды уақыттың детерминделген (кездейсоқ емес) функциясы ретінде қарастыруға болады. Байқалулардың N кездегі статистикалық ансамблі кездейсоқ (стохасты) процесс деп аталады.
4, 5, 6, 7.
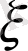 кездейсоқ шамасының математикалық күтімі немесе орта мәні дегеніміз
кездейсоқ шамасының математикалық күтімі немесе орта мәні дегеніміз
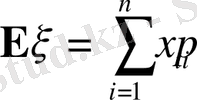 саны.
саны.
Математикалық күтімнің негізгі қасиеттері: егер
 кейбір кездейсоқ емес шама болса, онда
кейбір кездейсоқ емес шама болса, онда
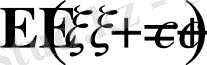 ,
,
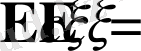 , егер
, егер
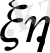 кез келген кездейсоқ шама болса, онда
кез келген кездейсоқ шама болса, онда
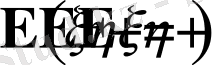 .
.
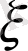 кездейсоқ шамасының дисперсиясы дегеніміз
кездейсоқ шамасының дисперсиясы дегеніміз
 саны.
саны.
Яғни,
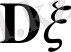 дегеніміз,
дегеніміз,
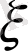 кездейсоқ шамасының өзінің орта мәні
кездейсоқ шамасының өзінің орта мәні
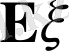 -ден ауытқу квадратының математикалық күтімі.
-ден ауытқу квадратының математикалық күтімі.
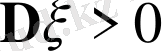 болатыны айқын.
болатыны айқын.
Математикалық күтім мен дисперсия -
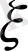 кездейсоқ шамасының негізгі сандық характеристикалары.
кездейсоқ шамасының негізгі сандық характеристикалары.
Егер де біз
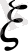 кездейсоқ шамасын көп рет бақылып,
кездейсоқ шамасын көп рет бақылып,
 шамаларын алсақ, онда олардың арифметикалық ортасы осы кездейсоқ шамасының математикалық күтімі
шамаларын алсақ, онда олардың арифметикалық ортасы осы кездейсоқ шамасының математикалық күтімі
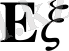 -ге жуық болады:
-ге жуық болады:
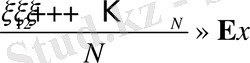 .
.
Дисперсия
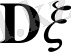 дегеніміз осы кездейсоқ мәндерінің орта мәні
дегеніміз осы кездейсоқ мәндерінің орта мәні
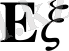 -ден ауытқуын сипаттайды.
-ден ауытқуын сипаттайды.
 .
.
Дисперсияның негізгі қасиеттері: егер
 кейбір кездейсоқ емес шама болса, онда
кейбір кездейсоқ емес шама болса, онда
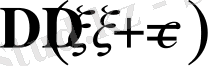 ,
,
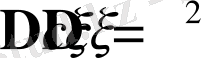 .
.
Ықтималдылықтар теориясында тәуелсіз кездейсоқ шамалар түсінігі өте маңызды. Егер
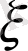 және
және
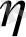 кездейсоқ шамалары тәуелсіз болса, онда келесі қатынастар дұрыс:
кездейсоқ шамалары тәуелсіз болса, онда келесі қатынастар дұрыс:
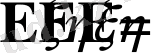 ,
,
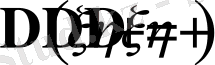 .
.
Кездейсоқ шама
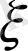 үзіліссіз деп аталады, егер ол
үзіліссіз деп аталады, егер ол
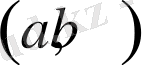 интервалынан кез келген мән қабылдаса.
интервалынан кез келген мән қабылдаса.
Үзіліссіз
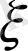 кездейсоқ шамасы, оның мүмкін болатын мәні жататын
кездейсоқ шамасы, оның мүмкін болатын мәні жататын
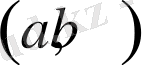 интервалымен және ықтималдылықтар тығыздығы, немесе
интервалымен және ықтималдылықтар тығыздығы, немесе
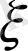 - дің үлестіру тығыздығы, деп аталатын
- дің үлестіру тығыздығы, деп аталатын
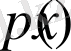 функциясымен анақталады.
функциясымен анақталады.
Мұнда
 және
және
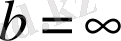 болуы да мүмкін. Бірақ тығыздық
болуы да мүмкін. Бірақ тығыздық
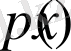 келесі екі шартты қанағаттандыруы тиіс: 1)
келесі екі шартты қанағаттандыруы тиіс: 1)
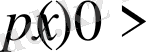 ; 2)
; 2)
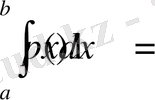 .
.
Үзіліссіз кездейсоқ шамасының математикалық күтімі немесе орта мәні дегеніміз
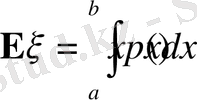 .
.
Айталық, жоғарғыдай
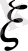 кездейсоқ шамасының тығыздығы
кездейсоқ шамасының тығыздығы
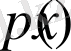 болсын. Кез келген үзіліссіз
болсын. Кез келген үзіліссіз
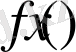 функциясын алып,
функциясын алып,
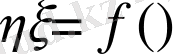 кездейсоқ шамасын қарастырайық. Онда
кездейсоқ шамасын қарастырайық. Онда
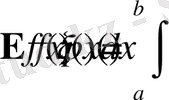 . Осындай формуланы дискретті кездейсоқ шамаға да жазуға болады
. Осындай формуланы дискретті кездейсоқ шамаға да жазуға болады
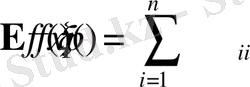 . Бір жағынан, жалпы жағдайда,
. Бір жағынан, жалпы жағдайда,
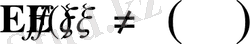 .
.
Тығыздығы
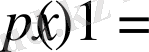 -ге тең,
-ге тең,
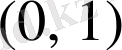 интервалында анықталған,
интервалында анықталған,
 кездейсоқ шамасы
кездейсоқ шамасы
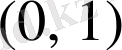 интервалында бірқалыпты үлестірілген
деп аталады.
интервалында бірқалыпты үлестірілген
деп аталады.
Шынында да,
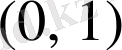 интервалында жатқан қандайда да бір
интервалында жатқан қандайда да бір
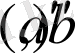 интервалын алсақ, онда
интервалын алсақ, онда
 кездейсоқ шамасы осы
кездейсоқ шамасы осы
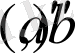 интервалында жату ықтималдылығы
интервалында жату ықтималдылығы
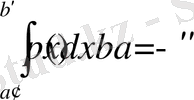 , яғни осы интервалдың ұзындығына тең. Егер
, яғни осы интервалдың ұзындығына тең. Егер
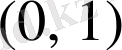 интервалын ұзындықтары бірдей, кез келген
интервалын ұзындықтары бірдей, кез келген
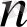 интервалдарға бөлсек, онда
интервалдарға бөлсек, онда
 кездейсоқ шамасының осы иентервалдардың кез келген біреуінде жату ықтималдылықтары бірдей.
кездейсоқ шамасының осы иентервалдардың кез келген біреуінде жату ықтималдылықтары бірдей.
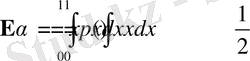 ,
,
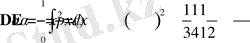 .
.
Нормальды кездейсоқ шамалары.
Нормальды немесе Гаусс кездейсоқ шамасы дегеніміз, барлық
 осінде анықталған және тығыздығы
осінде анықталған және тығыздығы
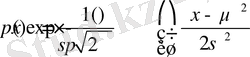 -ға тең
-ға тең
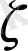 кездейсоқ шамасы, мұндағы
кездейсоқ шамасы, мұндағы
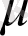 мен
мен
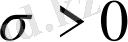 - сандық параметрлер.
- сандық параметрлер.
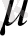 параметрі
параметрі
 қисығының формасын өзгертпейді: тек қана оны
қисығының формасын өзгертпейді: тек қана оны
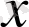 осі бойымен жылжытады, ал
осі бойымен жылжытады, ал
 параметрі өзгерсе, онда қисықтың да формасы өзгереді.
параметрі өзгерсе, онда қисықтың да формасы өзгереді.
 .
.
Кез келген
 ықтималдылығы
ықтималдылығы
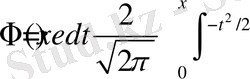 - ықтималдылықтар интегралы деп аталатын функциясының таблицалық мәндерімен анықталады. Ықтималдылықты табу ережесі бойынша
- ықтималдылықтар интегралы деп аталатын функциясының таблицалық мәндерімен анықталады. Ықтималдылықты табу ережесі бойынша
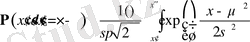 . Енді осы интегралда
. Енді осы интегралда
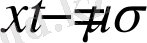 ауыстыруын жасасақ, онда
ауыстыруын жасасақ, онда
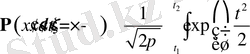 , мұндағы
, мұндағы
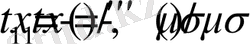 . Бұдан шығатын
. Бұдан шығатын
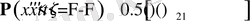 ,
,
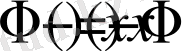 .
.
Ықтималдық қателігі.
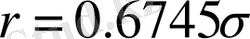 шамасы үшін
шамасы үшін
 мәндерін алайық. Онда
мәндерін алайық. Онда
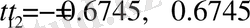 болады және
болады және
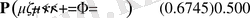 немесе
немесе
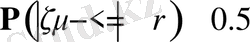 . Бұған қарама қарсы теңсіздіктің де ықтималдылығы 0. 5 болады, яғни
. Бұған қарама қарсы теңсіздіктің де ықтималдылығы 0. 5 болады, яғни
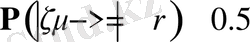 (
(
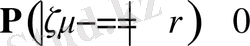 , себебі
, себебі
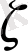 кездейсоқ шамасы үзіліссіз) .
кездейсоқ шамасы үзіліссіз) .
Осы, соңғы формулалардан алатынымыз:
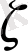 -дің
-дің
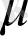 -ден
-ден
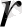 -ға үлкен немесе
-ға үлкен немесе
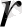 -ға кіші болып ауытқулары бірдей ықтималды. Сондықтан да
-ға кіші болып ауытқулары бірдей ықтималды. Сондықтан да
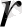 -ді
ықтималдық қателігі
дейміз.
-ді
ықтималдық қателігі
дейміз.
Кездейсоқ сигналдар - белгілі бір заңдылықпен өзгермейтін, белгіленген уақытта қандай болатынын алдын ала айтуга болмайтын сигнал. Кездейсоқ сигналдар тұрақты және тұрақсыз, эргодикалық немесе эргодикалық емес және Марковтық немесе Марковтық емес болып бөлінеді.
Тұрақты кездейсоқ сигналдар - ықтималдық тығыздыгы уақыт өлшемінің басталатын жеріне байланысты болмайтын кездейсок сигналдар. Тұрақты кездейсоқ сигналдардың сипаттамалары уақыт бойынша тұрақты болады.
Эргодикалық кездейсоқ сигналдар. Тұрақты кездейсоқ сигналдардың біразы эргодикалық қасиетте болады. Егер барлық тұрақты кездейсоқ сигналдардың (ансамбль бойынша) орта шамасы оған қатысатын мүшелердің біреуінің ұзақ уақыт бойынша орта шамасына тең болса, онда оны эргодикалық деп атайды. Эргодикалық сигналда көп сигналдарды бақылап талдаудың орнына тек бір сигналды ғана ұзақ уақыт бақылап шешім шығаруга болады.
Кездейсоқ сигналдарды жіктеу. Кездейсоқ сигнал деп, мәні алдын ала белгілі және тек кейбір ықтималдықпен ғана болжануы мүмкін уақыт функциясын атайды. Кездейсоқ сигнал кездейсоқ физикалық шаманы немесе физикалық процесті бейнелейді, оның үстіне бірлік бақылауда тіркелген сигнал қайталанған бақылаулар кезінде жаңғыртылмайды және айқын математикалық тәуелділікпен сипаттала алмайды. Кездейсоқ сигналды тіркеу кезінде кездейсоқ процестің ықтимал нұсқаларының (нәтиже) бірі ғана жүзеге асырылады, ал процесті тұтастай жеткілікті түрде толық және дәл сипаттауды тек бақылауды көп рет қайталағаннан және сигналды жүзеге асыру ансамблінің белгілі бір статистикалық сипаттамаларын есептеп шығарғаннан кейін жүргізуге болады. Кездейсоқ сигналдардың негізгі статистикалық сипаттамалары ретінде төмендегілерді қабылдайды:
а) мәндерінің белгілі бір аралығында сигнал шамасын табу ықтималдығын үлестіру заңы;
б) сигнал қуатын спектрлік үлестіру.
Ықтималдық теориясында зерттелетін барлық кездейсоқ құбылыстарды үш топқа бөлуге болады: кездейсоқ оқиғалар; кездейсоқ
Кездейсоқ шамаларды сипаттайтын сандық, статистикалық сипаттамалар мыналар болып табылады:
Ықтималдықтың үлестірім функциялары.
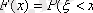
(2. 16)
Берілген функция Х кездейсоқ шамасы нақты таңдап алынған х мәнінен аспау ықтималдығын көрсетеді. Егер Х кездейсоқ шамасы дискретті болып табылатын болса, онда F(x) солай дискретті функция болып табылады, егер Х үздіксіз шама болса, онда F(x) үздіксіз функция.
Ықтималдықтың үлестірім тығыздығы.
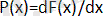 (2. 17)
(2. 17)
Берілген сипаттама кездейсоқ шама мәнінің х’ нүктесі төңірегінде dx кіші аралығына, яғни штрихталған аймаққа түсу ықтималдығын көрсетеді.
Математикалық үміт.
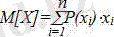
(2. 18)
мұнда хi - кездейсоқ шама мәні; Р(хi) - осы мәндердің пайда болу ықтималдығы; n - кездейсоқ шаманың ықтимал мәндерінің саны.
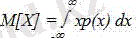
(2. 19)
мұнда р(х) - үздіксіз кездейсоқ шаманың ықтималдық тығыздығы. Өзінің мағынасы бойынша математикалық үміт кездейсоқ шаманың орташа және анағұрлым ықтимал мәнін көрсетеді, яғни осы мәнді кездейсоқ шама анағұрлым жиі қабылдайды. (2. 17) өрнегі, егер кездейсоқ шама дискретті болып табылатын болса, ал (2. 18) өрнегі, егер ол үздіксіз болып табылатын болса, қолданылады. M[X] белгісі, квадрат жақшаларда көрсетілген кездейсоқ шаманың математикалық үміті үшін арнайы болып табылады, алайда кейде mх немесе m белгілері пайдаланылады.
Дисперсия.
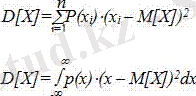
(2. 20)
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz