Алгебралық есептерді геометриялық әдістермен шешудің әдістемелік негіздері


Негізгі бөлім
І. Мәтіндік есептерді геометриялық әдіспен шешу
Көптеген математикалық тапсырмалардың бірнеше шығарылу жолдары бар. Тапсырмаларды шешудің ең тиімді жолдарын қарастыру математикалық дайындықтың шығар шыңы. Алгебралық тапсырмалардың шешімдерін табудың ең бір қажетті әдісі ол геометриялық түсіндірме әдісі. Немесе мұндай әдіспен шешілетін тапсырмаларды геометриялық алгебра деп атайды.
Математиканы оқытуда геометрия курсы үлкен орын алады. Математикаға бөлінген уақыттың 40%-ін геометрия алады. Геометрияны оқытудың басты мақсаттарының бірі - оның теориялық негіздерін білу және оларды практикада қолдану дағдыларын меңгеру. Сонымен қатар логикалық ойлауды, дәлелдеу қабілетін, талқылауларды себептеу, ойды дәл және анық тұжырымдай білу мәселелері де маңызды міндеттер болып табылады.
Геометрия - логикалық ойлауға, кеңістікті қиялмен елестетуге деген мүмкіндіктерге бай бірегей мектеп пәні. Ендеше неге бұл әлеуетті, ереже ретінде алгебра сабағында қолданбасқа? Алгебра мен геометрияны тұтас бір құрылым екенін естен шығарып, үнемі оларды екі бөлек пән ретінде қарастырады.
Бұл жұмысқа мынадай мақсаттар қойылды: есепті геометриялық тұрғыдан шешуде зор мүмкіндік туғызу, нақты алгебралық мәселелерді геометриялық жолмен шешудің артықшылғын көрсету.
Міндеттері:
- Мәтіндік есептерді геометриялық әдіспен шешу
- Қозғалысқа берілген есептер
- Жұмысқа берілген есептер
- Тригонометриялық есептерді геометриялық әдіспен шешу
- Алгебралық есептерді шешудің геометриялық әдістері
- - Параметрмен берілген есептерді геометриялық тәсілмен шешу
Зерттеу пәні: Есептерді шешудің геометриялық әдісі.
Зерттеу аймағы: Алгебралық тапсырмалар.
Зерттеу әдісі: Ұқсастық, қорыту, ғылыми әдебиеттерге анализ.
Геометрия курсының көкейкесті мәселелері ол - бұл курстың мазмұнының ғылыми құндылығын, оқу материалдарының түсініктілігін арттыру, мазмұнды геометриялық есептердің ролін күшейту. Логикалы-математикалық жүйелі дағдыны қалыптастру үшін қазіргі кезде есептерді шығарудың тек бір ғана әдісімен тоқталып қалу жеткіліксіз. Қосымша әдістерін де геометриялық емес есептерді геометиялық жолмен шығару әдістерін пайдалануға болады. Геометрия курсы қандай жолмен құрылмасын онда міндетті түрде теоремаларды дәлелдеудің, есептерді шығарудың әртүрлі әдістері қарастырылады. Сонымен алгебра курсында қарастырылатын есептерді геометрялық жолмен шығарыруының түрлі тәсілдерін қарастырайық.
І. Мәтіндік есептерді геометриялық әдіспен шешу
1. 1 Қозғалысқа берілген есептер
Математика курсының материалдарын оқытуда математикалық есептерді шешудің әртүрлі тәсілдері қарастырылады.
Есептерді геометриялық тәсілмен шешу әдісі Евклид заманында (б. э. д IIIғ) пайда болған және тек қана геометрияда емес алгебрада да қолданылған. Оның алгебрадағы қолданысының бір ерекшелігі - Евклид есептердің шешімін геометриялық салулар мен геометрия заңдарының көмегімен пайымдаған. Осылайша геометриялық алгебра дамыды. Біз алгебралық есептерді геометриялық тәсілдермен шығаруда геометриялық сызбалардың, геометрия заңдылықтарының, аналитикалық тәсіл элементтерінің (теңдеулер, арифметикалық өрнектер т. б) қолданыстарын үйренеміз. Мәтіндік есеп шартының геометриялық берілуін осы есептің геометриялық моделі деп атаймыз.
Алгебра курсында мәтіндік есептердің геометриялық моделінің 4 негізгі түрін қолдануға болады: а) бірөлшемді (сызықтық) диаграммалар; б) екіөлшемді диаграммалар; в) графикалық үлгілер; г) тапсырмада берілген фигуралардың сызбасы (геометриялық мазмұнды есептерде) .
Есепті геометриялық тәсілмен шығару 3 кезең арқылы жүзеге асады:
1) есептің геометриялық моделін кұру, яғни оны геометриялық тілге келтіру;
2) пайда болған геометриялық есептің шешімі;
3) нәтижесін геометриялықтан табиғиға айналдыру.
Осы кезеңдердің орындалуын алгебралық есептерді алғашқы 3 түрдің геометриялық моделіне сүйене отырып шешуде толығырақ қарастырамыз.
Сызықтық диаграмма мен кесінді ұзындығы қасиетінің қолданылуы.
Сызықтық диаграмма - ұзындығы қарастырылып отырған шаманың сандық мәніне сәйкес келетін бір немесе бірнеше кесінді. Алгебра курсында сызықтық диаграммамен шешілетін есептер екі түрде беріледі: 1) дәл сол уақытта бір ғана оқиға суреттеледі; 2) екі оқиға берілген: бастапқы және соңғы.
Бірінші түрдегі есепті шешуде сызықтық диаграмма статистикалық модель ретінде қолданылады, яғни орындау барысында өзгермей иллюстративті қызмет атқарады. Екінші түрдегі есептер сызықтық диаграмманы көбірек қажет етеді. Бұл есептерді осы тәсілмен шешу барысы екі түрлі : алдымен бастапқы (соңғы) объект қимылын білдіретін диаграмма, ал содан кейін есеп шарты бойынша қайтадан соңғы (бастапқы) жағдай орындалатындай өзгереді.
1- есеп: Көкөніс қоймасының біреуінде екіншісіне қарағанда 3 есе артық картоп бар. Бірінші қоймадан 450 т картоп алынып, ал екіншіге 120 т картоп қосқанда екі қоймадағы картоптар салмағы тең болды. Бастапқыда әр қоймада қанша тонна картоп болды?
I. Есепті оқығаннан кейін оқушылар мынадай сұрақтарға жауап беруі тиісті:
1) Есепте қанша оқиға қарастырылады? (Екі: бастапқы және соңғы)
2) Диаграмманы қай оқиғадан бастап салу керек? (Бастапқы оқиғадан бастап соңғы оқиғаға көшу немесе соңғы оқиғаға байланысты диаграмма құрып бастапқыға көшуге болады. Бірінші нұсқаны қарастырамыз) .
3) Бастапқы оқиға диаграммасы қалай салынады? (Біреуі екіншісінен 3 есе үлкен болатындай екі кесінді салынады. )
Оқушылар осы шарттар бойынша диаграмма салып, есепті әрі қарай талқылайды.
4) Бастапқы оқиға мен соңғы оқиғаны қалай бейнелеуге болады? (Бірінші кесіндіден 450 т -ны бейнелейтін кесіндіні алып, екінші бөлігіне 120 т -ны бейнелейтін кесінді қосамыз. )
5) Бөліктер кез келген түрде алына ма? (Жоқ, нәтижесінде екі қоймада да картоптар салмағы тең болғандықтан, қайта қосылған кесінділер тең болу керек)
Осы айтылғандарды орындағаннан кейін соңғы оқиғаға байланысты диаграмма құрылады.
Салынған сызықтық диаграмма шешімі кесінді ұзындығының қасиетіне негізделетін алгебралық есепті геометриялық түрге келтіреді. Шешімін жүйе құрмай-ақ, диаграммадан қарап та білуге болады.
Алдымен диаграммада берілгендерді жазып алу керек. Содан кейін сызбада кейбір мәндер белгілі көрініп тұрғандықтан бірте-бірте қысқаша түрге көше береміз.
1- тәсіл
AB кесіндісі бірінші қоймадағы картоптар мөлшері (1-сурет), CD екінші қоймадағы картоп мөлшері. АВ = 3CD қоймадағы картоптар айырмашылығы.
BK бірінші қоймадан алынған, ал DE екінші қоймаға әкелінген картоп мөлшері. АК = CE қоймада қалған картоптар мөлшері.
BM = 2AM, DE = MK (салу бойынша) .
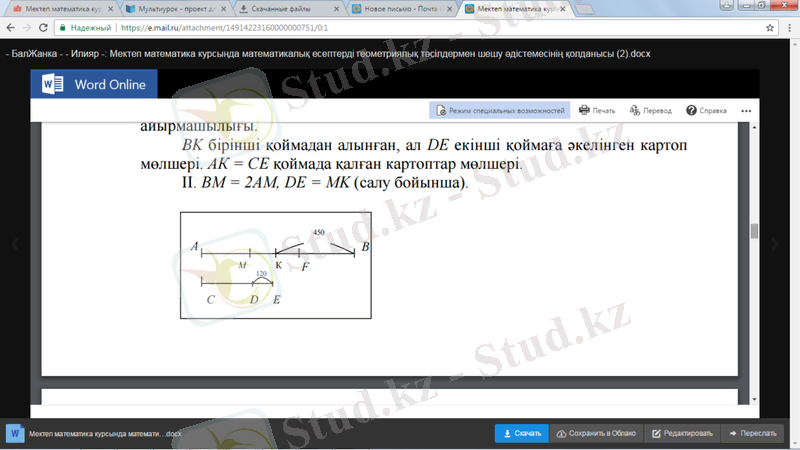
MB = MK = KB = 120+450 = 570. AM = 570:2 = 285. CD = AM=285, AB = 3CD = 3˟285 = 855.
Жауабы: Бірінші қоймада 855 т картоп болды, екіншіде 285 т .
2- тәсіл.
АК = CE = x болсын, онда: х+450 = 3(x-120), бұда н х = 405 , бұдан CD = 405 - 120 = 285. AB = 855.
3 - тәсіл.
CD = BF = FM = x болсын, BM = 2x, онда BM - MK = 450 , бұдан x = 285. Яғни, CD = 285, AB = 855.
4 - тәсіл.
CD = x болсын, онда AB = 3x. AK = CE болғандықтан x + 120 = 3x - 450
x = 285.
Екіөлшемді диаграммалар мен ауданның қасиетін қолдану.
Қарастырылып отырған өлшем басқа екі өлшемнің көбейтіндісі ретінде келтірілетін тапсырмаларды тіктөртбұрыштың ауданы (параллелограмм, үшбұрыш), яғни екіөлшемді диаграммалар көмегімен шешуге болады. Екіөлшемді диаграмма бір немесе бірнеше тіктөртбұрыштар ауданынан құралуы мүмкін.
Егер ескеретін болсақ бөлшек-рационал теңдеулермен оқушылар 8 сыныпта танысады. Екіөлшемді диаграмма бұл есепті сызықтық теңдеу арқылы шешуге мүмкіндік береді.
Геометриялық тәсіл. Бұл есепті шешпес бұрын екіөлшемді диаграмма түріндегі геометриялық ұғымдармен сызықтық диаграмма түріндегі геометриялық ұғымдар арасындағы байланысты анықтап алу керек. Ол үшін оқушылар сызықтық диаграмма қолданған есепте бөліктер бір ғана өлшем ұзындығын беретіндігін байқауы керек. Олар параллель түзулер бойында орналасады. Екі түрлі өлшем берілген есептерде бөліктер екі түрлі өлшемдерді білдіреді және тіктөртбұрыштың іргелес қабырғалары болатындай екі перпендикуляр түзу бойында белгіленеді. Пайда болған сурет екіөлшемді диаграмманы береді.
Есепте тең өлшемдер берілгендіктен, қайықпен жүрілген жолды жылдамдық пен уақыттың көбейтіндісі ретінде алуға болады.
2- есеп
Катер өзен ағысымен 4 сағат ішінде өзінің 2 сағат өзен ағысына қарсы жүрген жолынан 2, 4 есе көп жол жүрді. Егер өзен ағысының жылдамдығы 1, 5 км/сағ болса, онда катердің тұнық судағы жылдамдығы қандай?
Катердің өзен ағысына қарсы жүрген жолының екіөлшемді диаграммасын оқушыларға өз бетімен орындап сызуға болады. Олардың жіберген қателіктерін түзете отыру керек: тіктөртбұрыштар бөлек салынады, олардың биіктіктері әртүрлі, өйткені тіктөртбұрыш биіктігін көрсететін қайықтың өзен ағысымен және өзен ағысына қарсы жүзген уақыты әртүрлі. Осылайша ауданын оңай табуға болатын екі тіктөртбұрыш пайда болады.
I. Алгебралық тәсілмен шешкенде мынадай теңдеу шығады.
x - катердің тұнық судағы жылдамдығы
Катердің өзен ағысымен жүзген жолы S = 4*(x+1, 5)
Катердің өзен ағысына қарсы жүзген жолы S = 2*(x-1, 5)
Есеп шарт бойынша: 4*(x+1, 5) = 2*(x-1, 5) *2, 4
х = 16, 5
II. MNOP үшбұрышының MN қабырғасы катердің өзен ағысымен жүргендегі жылдамдығы. MP катердің осы жылдамдықпен жүзіп өткен уақыт аралығын білдіреді. Егер х деп катердің тұнық судағы жылдамдығын белгілесек, онда MN = x + 1, 5 (км/сағ) . MP = 4(сағ) .

MNOP тіктөртбұрышының ауданы қайықтың өзен ағысымен жүзгендегі арақашықтығына тең : S 1 = MN*MP
NK = x - 1, 5 - катердің өзен ағысына қарсы жүзгендегі жылдамдығы (км/сағ) онда KL катердің өзен ағысына қарсы жүзген уақыты. KL = 12MP = 2
NKLQ тіктөртбұрышының ауданы катердің өзен ағысына қарсы жүзгендегі жолын білдіреді. S 2 = NK* KL
S 1 = 2, 4 S 2
(x+1, 5) *4 = 2, 4*( x -1, 5) *2
4x+6=4, 8x - 7, 2
- 0, 8x = - 13, 2
x = 16, 5
3 - есеп. Автобус А қаласынан В қаласына 40 км/сағ жылдамдықпен бет алды. Автобус 30 км жол жүргеннен кейін, А қаласынан 60 км/сағ жылдамдықпен шыққан автокөлік В қаласына
 сағ автобустан кейін келді. Екі қаланың арақашықтығын тап.
сағ автобустан кейін келді. Екі қаланың арақашықтығын тап.
S, км
B
 c
c
M D
N
30км
А
 с С t, уақыт
с С t, уақыт
АВ - автобустың қозғалыс графигі
СD - автокөліктің қозғалыс графигі
Шешуі: х км - екі қаланың арақашықтығын табу.
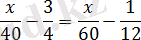
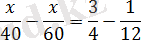
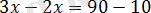
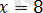 0
0
1. 2 Жұмысқа берілген есептер
Екі жұмысшы бірігіп жұмысты 12 күнде бітірер еді. Егер біреуі ғана жұмыстанып, жарты жұмысын бітірген соң екінші жұмысшы жалғастырса, барлық жұмыс 25 күнде бітеді. Барлық жұмысты әр жұмысшы бөлек орындаса неше күнде бітіреді?
Шешуі: Бірінші жұмысшы екінші жұмысшыға қарағанда тезірек жұмыс жасайды деп есептейік. AN кесіндісі - бірінші жұмысшының графигі, ал BD кесінді - екінші жұмысшының графигі. AQ екеуінің бірігіп жасаған уақыты. AQ=12 сағ. NK‖ BD жүргізсек, онда AK=50, QK=38, ∆BPN∾∆APD
12(12+x) =x(38-x)
x2-26x+144=0
x1=18 - жауабы бола алмайды, себебі бірінші жұмысшы екіншіге қарағанда тез жұмыс жасайды. Олай болса, бірінші жұмысшының уақыты 12+8=20 күн, ал екінші жұмысшыныкы 38-8=30 күн.
Жауабы: біріншісі 20 күнде, екіншісі 30 күнде.
Алгебралық есептерді шешудің геометриялық әдістері
2. 1. Тригонометриялық есептерді геометриялық әдіспен шешу
Көптеген тригонометриялық тапсырмаларды орындауда есептің шығарылуы не ұзаққа созылады не болмаса қиындықтар кездеседі. Ал геометриялық әдіспен шығару есепті біршама жеңілдетеді және есептің шығарылу жолы қысқаша әрі түсінікті болады. Тригонометриялық функцилар - ол белгілі геометриялық аппарат, сондықтан оларды да көрсету үшін қарапайым есептерден бастап көрсету керек.
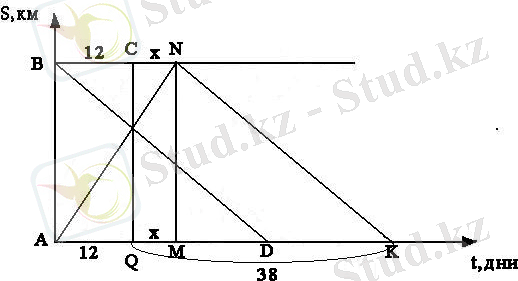
1 есеп. Есепте:
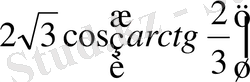
Шешуі: Кері тригонометриялық функцияның барлық белгілері осы - оң сандар, І - ширекте, демек сүйір бұрыш. Сондықтан оны тікбұрышты үшбұрыш арқылы табуға болады.
arctg2/3 - тангенсі 2/3 - ге тең тікбұрышты үшбұрыштың бұрышы. Демек, сүйір бұрышқа қарсы жатқан катеттің, сол бұрышқа іргелес катетке қатынасы 2:3. Пифагор теоремасы бойынша гипотенузасын табамыз.
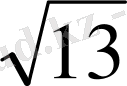
tgα=x
tgα=2/3, a=2, b=3, c=a 2 +b 2 =13
cosα=cb, cosarctg2/3=3/
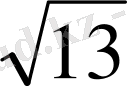 ⇔ 2
⇔ 2
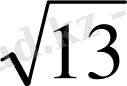 cosarctg2/3=2
cosarctg2/3=2
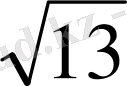 ∙3/
∙3/
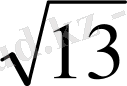 =6
=6
Жауабы: 6.
2 есеп. Дәлелдеу: cos 40°+cos 80° = cos 20°.
Шешуі:
Бірінші тәсіл (тең бүйірлі үшбұрыш) .
 АВ=ВС) тең бүйірлі үшбұрышын қарастырайық,
АВ=ВС) тең бүйірлі үшбұрышын қарастырайық,
 АВС=20°
АВС=20°
1) Мұндағы DЄBC, KЄBC, EЄAB және BK=KE=ED=DA=1.
2) BE= 2 cos 20°, АЕ = 1, ВК = 1, КD = 2 cos 40°,
DC=2 cos 80°.
3) АЕ +ЕВ = СD + DK + KB.
1 + 2 cos20° = 2 cos80° + 2 cos40° + 1,
cos40°+cos80° = cos20°.
Екінші тәсіл:
cos 40°+cos 80° = 2 cos 60° cos20° = 2*0, 5*cos 20° = cos 20°.
2. 2 Параметрмен берілген есептерді геометриялық тәсілмен шешу
Есеп. x2 + y2 = 1 болғандағы y = x + a белгісіз а параметрін табу керек.
Шешуі: x2 + y2 = 1 - центрі бас нүктесінде орналасқан және радиусы 1-ге тең.
Төбелері Оу осінде орналасқан «бұрыштар» пайда болады
y
1x
0
1
1
-1
1
-√2
Бұрыш»
 болғанда, шеңбермен қиылысады. Жауабы суреттен алынады.
a
{−√2 } болғандағы
a
{−√2 } ∪ (−1; 1) екі жауабы болады.
болғанда, шеңбермен қиылысады. Жауабы суреттен алынады.
a
{−√2 } болғандағы
a
{−√2 } ∪ (−1; 1) екі жауабы болады.
Жауабы: a = {−√2 } ∪ (−1; 1) .
ІІІ. Тарихи есептерде қолданылуы
3. 1Квадрат теңдеулерге берілген есептер
Есеп. ab=x2 теңдеуін шешу
Ежелгі гректердің шығару жолымен қарастырсақ, қабырғалары a және b болатын төртбұрышты ауданы осы төртбұрышқа тең квадратқа көшіру арқылы шығарған.
Салу:
- (a+b) кесіндісін салу
- (a+b) кесіндісіндісінің диаметріндей жарты шеңбер салу.
- Радиустарыaжәнеb-ға тең шеңберлер салынып, N нүктесінде қиылысып (a+b) кесіндісіне перпендикуляр түсіріледі. Оны х деп белгілейді.
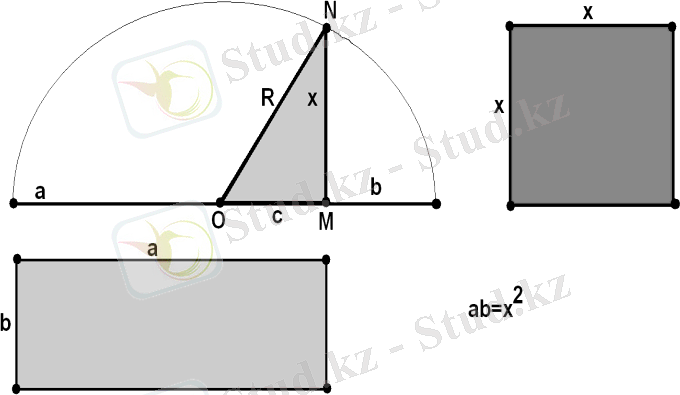
Дәлелдеуі. a>b болсын және R - шеңбер радиус. Онда 2R=a+b және R=b+c бұдан a+b=2b+2c, a-b=2c, с=(a-b) :2 . Бойынша R 2 =c2+x2
a 2 + 2 ab + b 2
4
ab=x2
a 2 − 2 ab + b 2
−
4
= x 2
3. 2 Арифметикалық пррогрессия
... жалғасы- Іс жүргізу
- Автоматтандыру, Техника
- Алғашқы әскери дайындық
- Астрономия
- Ауыл шаруашылығы
- Банк ісі
- Бизнесті бағалау
- Биология
- Бухгалтерлік іс
- Валеология
- Ветеринария
- География
- Геология, Геофизика, Геодезия
- Дін
- Ет, сүт, шарап өнімдері
- Жалпы тарих
- Жер кадастрі, Жылжымайтын мүлік
- Журналистика
- Информатика
- Кеден ісі
- Маркетинг
- Математика, Геометрия
- Медицина
- Мемлекеттік басқару
- Менеджмент
- Мұнай, Газ
- Мұрағат ісі
- Мәдениеттану
- ОБЖ (Основы безопасности жизнедеятельности)
- Педагогика
- Полиграфия
- Психология
- Салық
- Саясаттану
- Сақтандыру
- Сертификаттау, стандарттау
- Социология, Демография
- Спорт
- Статистика
- Тілтану, Филология
- Тарихи тұлғалар
- Тау-кен ісі
- Транспорт
- Туризм
- Физика
- Философия
- Халықаралық қатынастар
- Химия
- Экология, Қоршаған ортаны қорғау
- Экономика
- Экономикалық география
- Электротехника
- Қазақстан тарихы
- Қаржы
- Құрылыс
- Құқық, Криминалистика
- Әдебиет
- Өнер, музыка
- Өнеркәсіп, Өндіріс
Қазақ тілінде жазылған рефераттар, курстық жұмыстар, дипломдық жұмыстар бойынша біздің қор #1 болып табылады.



Ақпарат
Қосымша
Email: info@stud.kz